浙教版七年级数学下册试题 2.4 二元一次方程组的应用(含答案)
文档属性
| 名称 | 浙教版七年级数学下册试题 2.4 二元一次方程组的应用(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 97.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-14 00:00:00 | ||
图片预览




文档简介
2.4 二元一次方程组的应用
一.选择题
1.“阅读与人文滋养内心”,某校开展阅读经典活动.小明3天里阅读的总页数比小颖5天里阅读的总页数少6页,小颖平均每天阅读的页数比小明平均每天阅读的页数的2倍少10页,若小明、小颖平均每天分别阅读x页、y页,则下列方程组正确的是( )
A. B.
C. D.
2.今有人合伙购物,每人出8钱,会多3钱;每人出7钱,又差4钱,问人数、物价各多少?设有x人,商品的价格为y,依题意可列方程组为( )
A. B.
C. D.
3.在“幻方拓展课程”探索中,小明在如图的3×3方格填入了一些表示数的代数式,若图中各行、各列及对角线上的三个数之和都相等,则y﹣x=( )
A.2 B.4 C.﹣6 D.6
4.《孙子算经》是中国古代最重要的数学著作,约成书于四、五世纪.现在的传本共三卷,卷上叙述算筹记数的纵横相间制度和筹算乘除法;卷中举例说明筹算分数算法和筹算开平方法;卷下记录算题,不但提供了答案,而且还给出了解法.其中记载:“今有木,不知长短,引绳度之,余绳四尺五寸,屈绳量之,不足一尺.木长几何?”译文:“用一根绳子去量一根长木,绳子还剩余4.5尺,将绳子对折再量长木,长木还剩余1尺,问木长多少尺?”设绳子长x尺,木长y尺,可列方程组为( )
A. B.
C. D.
5.某果园现有桃树和杏树共500棵,计划一年后桃树增加3%,杏树增加4%,这样果园里这两种果树将增加3.6%,如果设该果园现有桃树和杏树分别为x棵,y棵,可列方程组为( )
A. B.
C. D.
6.中国古代人民在生产生活中发现了许多数学问题,在《孙子算经》中记载了这样一个问题,大意为:有若干人乘车,若每车乘坐3人,则2辆车无人乘坐;若每车乘坐2人,则9人无车可乘,问共有多少辆车,多少人,设共有x辆车,y人,则可列方程组为( )
A. B.
C. D.
7.某船顺水航行45千米需要3小时,逆水航行65千米需要5小时,若设船在静水中的速度为x千米时,水流速度为y千米时,则根据题意,可列方程组( )
A. B.
C. D.
8.如图,10块相同的小长方形墙砖拼成一个大长方形,设小长方形墙砖的长和宽分别为xcm和ycm,则两个小长方形的面积是( )
A.1200 B.1600 C.1800 D.2400
9.如图,在大长方形中放入6个形状、大小相同的小长方形,所标尺寸如图所示,则图中大长方形的面积是( )
A.96 B.112 C.126 D.140
10.《九章算术》中,一次方程组是由算筹布置而成的.如图1所示的算筹图,表示的方程组就是,类似地,图2所示的算筹图表示的方程组为( )
A. B.
C. D.
二.填空题
11.一条船顺流航行,每小时行20km,逆流航行,每小时行16km,则船在静水的速度 km/h.
12.街道为环卫工人发放口罩,如果每人发5个,还剩下3个,如果每人发6个,还缺5个,则一共有 名环卫工人.
13.我国古代《算法统宗》里有这样一首诗:我问开店李三公,众客都来住店中,一房七客多七客,一房九客一房空.诗中后两句的意思是:如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间房.设该店有客房x间,房客y人.可列方程组为: .
14.某车间有60名工人,每人平均每天可加工螺栓14个或螺母20个,要使每天加工的螺栓和螺母配套(1个螺栓配2个螺母),设应分配x人生产螺母,y人生产螺栓,依题意列方程组得 .
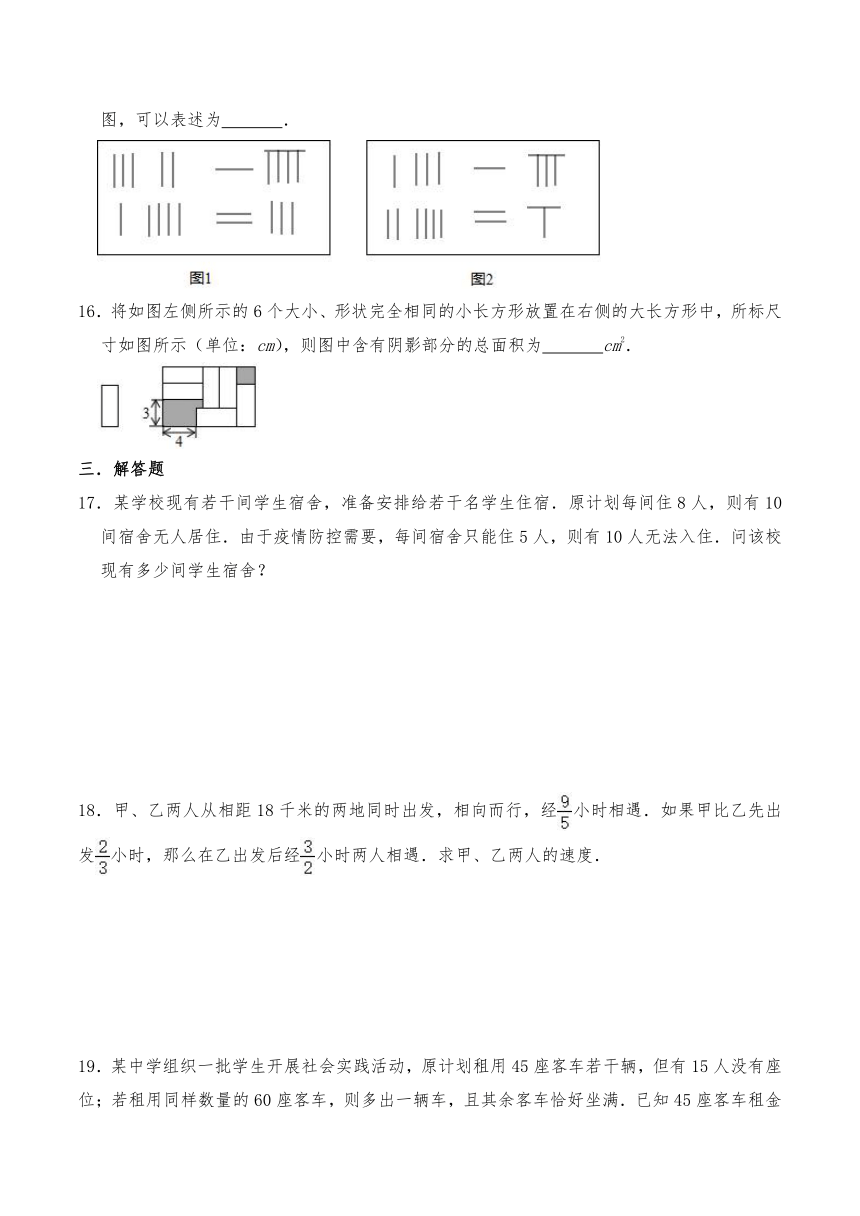
15.《九章算术》中的算筹图是竖排的,为看图方便,我们把它改成横排,如图1、图2,图中各行从左到右列出的算筹数分别表示未知数x,y的系数与相应的常数项.把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是.类似地,图2所示的算筹图,可以表述为 .
16.将如图左侧所示的6个大小、形状完全相同的小长方形放置在右侧的大长方形中,所标尺寸如图所示(单位:cm),则图中含有阴影部分的总面积为 cm2.
三.解答题
17.某学校现有若干间学生宿舍,准备安排给若干名学生住宿.原计划每间住8人,则有10间宿舍无人居住.由于疫情防控需要,每间宿舍只能住5人,则有10人无法入住.问该校现有多少间学生宿舍?
18.甲、乙两人从相距18千米的两地同时出发,相向而行,经小时相遇.如果甲比乙先出发小时,那么在乙出发后经小时两人相遇.求甲、乙两人的速度.
19.某中学组织一批学生开展社会实践活动,原计划租用45座客车若干辆,但有15人没有座位;若租用同样数量的60座客车,则多出一辆车,且其余客车恰好坐满.已知45座客车租金为每辆220元,60座客车租金为每辆300元.
(1)这批学生的人数是多少?原计划租用45座客车多少辆?
(2)若租用同一种客车,要使每位学生都有座位,应该怎样租用才合算?
20.在《二元一次方程组》这一章的复习课上,王老师让同学们根据下列条件探索还能求出哪些量:在我市“精准扶贫”工作中,甲、乙两个工程队先后接力为扶贫村庄修建条335米长的公路,甲队每天修建20米,乙队每天修建25米,一共用15天完成.
(1)小红同学根据题意,列出了一个尚不完整的方程组请写出小红所列方程组中未知数x,y表示的意义:x表示 ,y表示 ;并写出该方程组中?处的数应是 ,*处的数应是 ;
(2)小芳同学的思路是想设甲工程队一共修建了x米公路,乙工程队一共修建了y米公路.下面请你按照小芳的设想列出方程组,并求出乙队修建了多少天?
21.长沙市某公园的广]票价格如表所示:
购票人数 1~50人 51~100人 100人以上
票价 10元/人 8元/人 5元/人
某校九年级甲、乙两个班共100多人去该公园举行毕业联欢活动,其中甲班有50多人不到60人,乙班不足50人,如果以班为单位分别买门票,两个班一共应付920元;如果两个班联合起来作为一个团体购票,一共要付515元,问甲,乙两班分别有多少人?
22.某电器超市销售每台进价为80元、200元的A,B两种型号的电风扇,如表所示是六月份前2周的销售情况:(进价、售价均保持不变,利润=销售收入﹣进货成本)
销售时段 销售数量 销售收入
A种型号 B种型号
第一周 6 5 2100元
第二周 4 10 3400元
(1)求A、B两种型号的电风扇的销售单价.
(2)若超市一共采购这两种型号的电风扇共120台,售完后该超市能否实现利润为8000元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
23.为响应国家节能减排的号召,鼓励居民节约用电,各省先后出台了居民用电“阶梯价格”制度,如表中是某省的电价标准(每月),例如,方女士家5月份用电500度,电费=180×0.6+220×二档电价+100×三档电价=352元,李先生家5月份用电460度,交费316元.
阶梯 电量 电价
一档 0﹣180度 0.6元/度
二档 181﹣400度 二档电价
三档 400度及以上 三档电价
请解答下列问题
(1)若王先生家5月用电160度,则电费多少元?
(2)求二档电价和三档电价分别为多少?
(3)若何女士家5月用电600度,则电费多少元?
答案
一.选择题
C.D.C.B.B.A.A.D.D.B.
二.填空题
11.18.
12.8.
13..
14..
15..
16.17.
三.解答题
17.解:设该校现有x间学生宿舍,共安排y名学生住宿,
依题意,得:,
解得:.
答:该校现有30间学生宿舍.
18.解:设甲、乙两人的速度分别为x千米/小时、y千米小时,
,
解得,,
答:甲、乙两人的速度分别为4.5千米/小时、5.5千米/小时.
19.解:(1)设这批学生有x人,原计划租用45座客车y辆,
根据题意得:,
解得:.
答:这批学生有240人,原计划租用45座客车5辆.
(2)∵要使每位学生都有座位,
∴租45座客车需要5+1=6辆,租60座客车需要5﹣1=4辆.
220×6=1320(元),300×4=1200(元),
∵1320>1200,
∴若租用同一种客车,租4辆60座客车划算.
20.解:(1)根据方程组中第二个方程可得x是与甲队每天修建的长度相乘,y是与乙队每天修建的长度相乘,这样可得出x、y分别是甲、乙两队各自修路的天数,从而得到x+y=15,20x+25y=335;
故答案为:甲队修路的天数;乙队修路的天数;15;335;
(2)方程组为:,
由①得,x=335﹣y③,
将③式代入②式得,,
解得,y=175,
所以,乙队修建了175米,修建的天数为(天).
答:乙队修建了175米,修建了7天.
21.解:设甲班有x人,乙班有y人,
依题意,得:,
解得:.
答:甲班有55人,乙班有48人.
22.解:(1)设A种型号的电风扇的销售单价为x元,B种型号的电风扇的销售单价为y元,
依题意,得:,
解得:.
答:A种型号的电风扇的销售单价为100元,B种型号的电风扇的销售单价为300元.
(2)设采购A种型号的电风扇m台,B种型号的电风扇n台,
依题意,得:,
解得:.
答:能实现利润为8000元的目标,可采购A种型号的电风扇50台,B种型号的电风扇70台.
23.解:(1)160×0.6=96(元).
答:王先生家5月份应交电费96元.
(2)设二档电价为x元/度,三档电价为y元/度,
依题意,得:,
解得:.
答:二档电价为0.7元/度,三档电价为0.9元/度.
(3)180×0.6+220×0.7+(600﹣400)×0.9=442(元).
答:何女士家5月份应交电费442元.
一.选择题
1.“阅读与人文滋养内心”,某校开展阅读经典活动.小明3天里阅读的总页数比小颖5天里阅读的总页数少6页,小颖平均每天阅读的页数比小明平均每天阅读的页数的2倍少10页,若小明、小颖平均每天分别阅读x页、y页,则下列方程组正确的是( )
A. B.
C. D.
2.今有人合伙购物,每人出8钱,会多3钱;每人出7钱,又差4钱,问人数、物价各多少?设有x人,商品的价格为y,依题意可列方程组为( )
A. B.
C. D.
3.在“幻方拓展课程”探索中,小明在如图的3×3方格填入了一些表示数的代数式,若图中各行、各列及对角线上的三个数之和都相等,则y﹣x=( )
A.2 B.4 C.﹣6 D.6
4.《孙子算经》是中国古代最重要的数学著作,约成书于四、五世纪.现在的传本共三卷,卷上叙述算筹记数的纵横相间制度和筹算乘除法;卷中举例说明筹算分数算法和筹算开平方法;卷下记录算题,不但提供了答案,而且还给出了解法.其中记载:“今有木,不知长短,引绳度之,余绳四尺五寸,屈绳量之,不足一尺.木长几何?”译文:“用一根绳子去量一根长木,绳子还剩余4.5尺,将绳子对折再量长木,长木还剩余1尺,问木长多少尺?”设绳子长x尺,木长y尺,可列方程组为( )
A. B.
C. D.
5.某果园现有桃树和杏树共500棵,计划一年后桃树增加3%,杏树增加4%,这样果园里这两种果树将增加3.6%,如果设该果园现有桃树和杏树分别为x棵,y棵,可列方程组为( )
A. B.
C. D.
6.中国古代人民在生产生活中发现了许多数学问题,在《孙子算经》中记载了这样一个问题,大意为:有若干人乘车,若每车乘坐3人,则2辆车无人乘坐;若每车乘坐2人,则9人无车可乘,问共有多少辆车,多少人,设共有x辆车,y人,则可列方程组为( )
A. B.
C. D.
7.某船顺水航行45千米需要3小时,逆水航行65千米需要5小时,若设船在静水中的速度为x千米时,水流速度为y千米时,则根据题意,可列方程组( )
A. B.
C. D.
8.如图,10块相同的小长方形墙砖拼成一个大长方形,设小长方形墙砖的长和宽分别为xcm和ycm,则两个小长方形的面积是( )
A.1200 B.1600 C.1800 D.2400
9.如图,在大长方形中放入6个形状、大小相同的小长方形,所标尺寸如图所示,则图中大长方形的面积是( )
A.96 B.112 C.126 D.140
10.《九章算术》中,一次方程组是由算筹布置而成的.如图1所示的算筹图,表示的方程组就是,类似地,图2所示的算筹图表示的方程组为( )
A. B.
C. D.
二.填空题
11.一条船顺流航行,每小时行20km,逆流航行,每小时行16km,则船在静水的速度 km/h.
12.街道为环卫工人发放口罩,如果每人发5个,还剩下3个,如果每人发6个,还缺5个,则一共有 名环卫工人.
13.我国古代《算法统宗》里有这样一首诗:我问开店李三公,众客都来住店中,一房七客多七客,一房九客一房空.诗中后两句的意思是:如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间房.设该店有客房x间,房客y人.可列方程组为: .
14.某车间有60名工人,每人平均每天可加工螺栓14个或螺母20个,要使每天加工的螺栓和螺母配套(1个螺栓配2个螺母),设应分配x人生产螺母,y人生产螺栓,依题意列方程组得 .
15.《九章算术》中的算筹图是竖排的,为看图方便,我们把它改成横排,如图1、图2,图中各行从左到右列出的算筹数分别表示未知数x,y的系数与相应的常数项.把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是.类似地,图2所示的算筹图,可以表述为 .
16.将如图左侧所示的6个大小、形状完全相同的小长方形放置在右侧的大长方形中,所标尺寸如图所示(单位:cm),则图中含有阴影部分的总面积为 cm2.
三.解答题
17.某学校现有若干间学生宿舍,准备安排给若干名学生住宿.原计划每间住8人,则有10间宿舍无人居住.由于疫情防控需要,每间宿舍只能住5人,则有10人无法入住.问该校现有多少间学生宿舍?
18.甲、乙两人从相距18千米的两地同时出发,相向而行,经小时相遇.如果甲比乙先出发小时,那么在乙出发后经小时两人相遇.求甲、乙两人的速度.
19.某中学组织一批学生开展社会实践活动,原计划租用45座客车若干辆,但有15人没有座位;若租用同样数量的60座客车,则多出一辆车,且其余客车恰好坐满.已知45座客车租金为每辆220元,60座客车租金为每辆300元.
(1)这批学生的人数是多少?原计划租用45座客车多少辆?
(2)若租用同一种客车,要使每位学生都有座位,应该怎样租用才合算?
20.在《二元一次方程组》这一章的复习课上,王老师让同学们根据下列条件探索还能求出哪些量:在我市“精准扶贫”工作中,甲、乙两个工程队先后接力为扶贫村庄修建条335米长的公路,甲队每天修建20米,乙队每天修建25米,一共用15天完成.
(1)小红同学根据题意,列出了一个尚不完整的方程组请写出小红所列方程组中未知数x,y表示的意义:x表示 ,y表示 ;并写出该方程组中?处的数应是 ,*处的数应是 ;
(2)小芳同学的思路是想设甲工程队一共修建了x米公路,乙工程队一共修建了y米公路.下面请你按照小芳的设想列出方程组,并求出乙队修建了多少天?
21.长沙市某公园的广]票价格如表所示:
购票人数 1~50人 51~100人 100人以上
票价 10元/人 8元/人 5元/人
某校九年级甲、乙两个班共100多人去该公园举行毕业联欢活动,其中甲班有50多人不到60人,乙班不足50人,如果以班为单位分别买门票,两个班一共应付920元;如果两个班联合起来作为一个团体购票,一共要付515元,问甲,乙两班分别有多少人?
22.某电器超市销售每台进价为80元、200元的A,B两种型号的电风扇,如表所示是六月份前2周的销售情况:(进价、售价均保持不变,利润=销售收入﹣进货成本)
销售时段 销售数量 销售收入
A种型号 B种型号
第一周 6 5 2100元
第二周 4 10 3400元
(1)求A、B两种型号的电风扇的销售单价.
(2)若超市一共采购这两种型号的电风扇共120台,售完后该超市能否实现利润为8000元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
23.为响应国家节能减排的号召,鼓励居民节约用电,各省先后出台了居民用电“阶梯价格”制度,如表中是某省的电价标准(每月),例如,方女士家5月份用电500度,电费=180×0.6+220×二档电价+100×三档电价=352元,李先生家5月份用电460度,交费316元.
阶梯 电量 电价
一档 0﹣180度 0.6元/度
二档 181﹣400度 二档电价
三档 400度及以上 三档电价
请解答下列问题
(1)若王先生家5月用电160度,则电费多少元?
(2)求二档电价和三档电价分别为多少?
(3)若何女士家5月用电600度,则电费多少元?
答案
一.选择题
C.D.C.B.B.A.A.D.D.B.
二.填空题
11.18.
12.8.
13..
14..
15..
16.17.
三.解答题
17.解:设该校现有x间学生宿舍,共安排y名学生住宿,
依题意,得:,
解得:.
答:该校现有30间学生宿舍.
18.解:设甲、乙两人的速度分别为x千米/小时、y千米小时,
,
解得,,
答:甲、乙两人的速度分别为4.5千米/小时、5.5千米/小时.
19.解:(1)设这批学生有x人,原计划租用45座客车y辆,
根据题意得:,
解得:.
答:这批学生有240人,原计划租用45座客车5辆.
(2)∵要使每位学生都有座位,
∴租45座客车需要5+1=6辆,租60座客车需要5﹣1=4辆.
220×6=1320(元),300×4=1200(元),
∵1320>1200,
∴若租用同一种客车,租4辆60座客车划算.
20.解:(1)根据方程组中第二个方程可得x是与甲队每天修建的长度相乘,y是与乙队每天修建的长度相乘,这样可得出x、y分别是甲、乙两队各自修路的天数,从而得到x+y=15,20x+25y=335;
故答案为:甲队修路的天数;乙队修路的天数;15;335;
(2)方程组为:,
由①得,x=335﹣y③,
将③式代入②式得,,
解得,y=175,
所以,乙队修建了175米,修建的天数为(天).
答:乙队修建了175米,修建了7天.
21.解:设甲班有x人,乙班有y人,
依题意,得:,
解得:.
答:甲班有55人,乙班有48人.
22.解:(1)设A种型号的电风扇的销售单价为x元,B种型号的电风扇的销售单价为y元,
依题意,得:,
解得:.
答:A种型号的电风扇的销售单价为100元,B种型号的电风扇的销售单价为300元.
(2)设采购A种型号的电风扇m台,B种型号的电风扇n台,
依题意,得:,
解得:.
答:能实现利润为8000元的目标,可采购A种型号的电风扇50台,B种型号的电风扇70台.
23.解:(1)160×0.6=96(元).
答:王先生家5月份应交电费96元.
(2)设二档电价为x元/度,三档电价为y元/度,
依题意,得:,
解得:.
答:二档电价为0.7元/度,三档电价为0.9元/度.
(3)180×0.6+220×0.7+(600﹣400)×0.9=442(元).
答:何女士家5月份应交电费442元.
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
