七年级数学下册试题 5.4 分式的加减 浙教版(含答案)
文档属性
| 名称 | 七年级数学下册试题 5.4 分式的加减 浙教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 90.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-21 15:52:49 | ||
图片预览



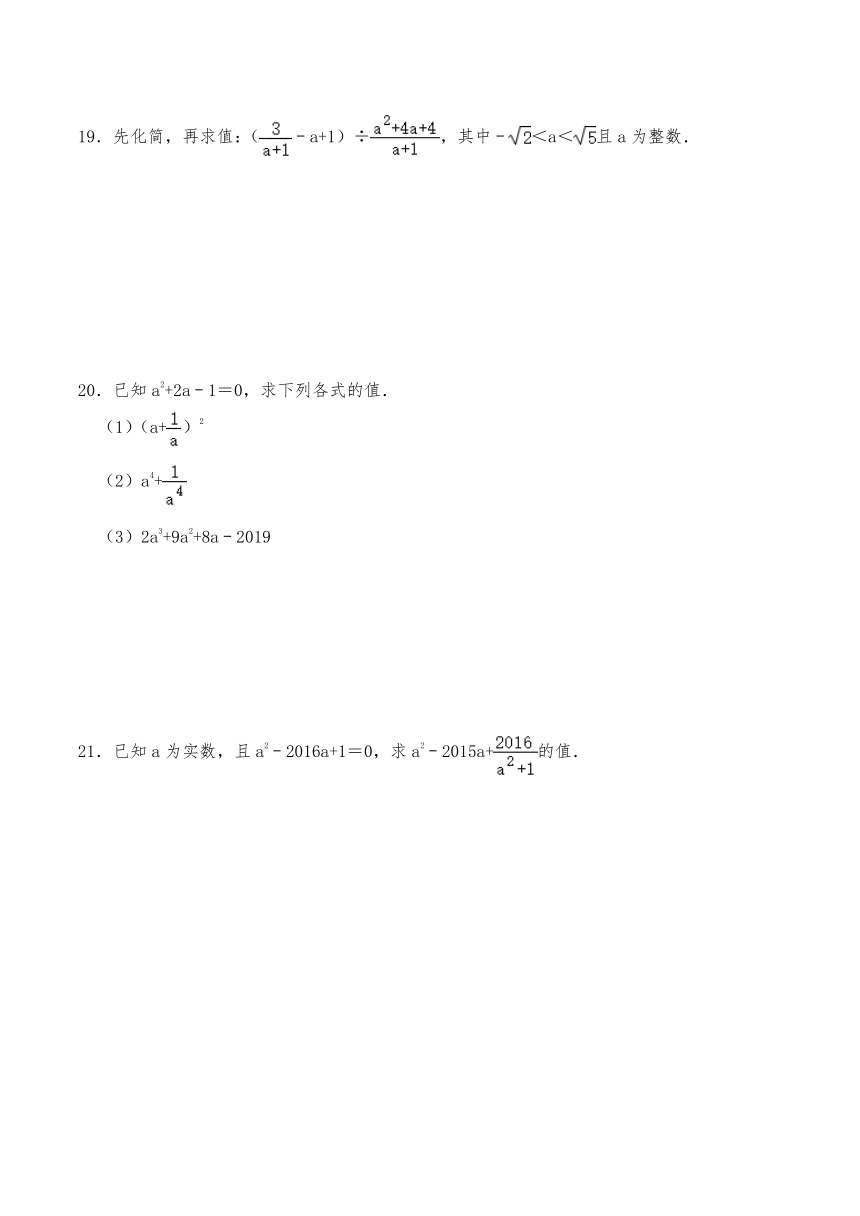
文档简介
5.4 分式的加减
一.选择题
1.与的最简公分母是( )
A.a(a+b) B.a(a﹣b)
C.a(a+b)(a﹣b) D.a2(a+b)(a﹣b)
2.把,通分,下列计算正确是( )
A.=,=
B.=,=
C.=,=
D.=,=
3.化简的结果为( )
A.a﹣b B.a+b C. D.
4.计算(1﹣)(m+1)的结果是( )
A.1 B.﹣1 C.m D.﹣m
5.如果m﹣n=1,那么代数式的值为( )
A.﹣3 B.﹣1 C.1 D.3
6.如果x2+2x﹣2=0,那么代数式 ﹣的值为( )
A.﹣2 B.﹣1 C.1 D.2
7.已知实数a,b为方程x2﹣6x+4=0的解,且a≠b,则+的值是( )
A.7 B.﹣7 C.11 D.﹣11
8.已知分式A=,B=+,其中x≠±2,则A与B的关系是( )
A.A=B B.A=﹣B C.A>B D.A<B
9.x为整数,且的值也为整数,那么符合条件的x的个数为( )
A.4个 B.3个 C.2个 D.1个
二.填空题
10.化简:= .
11.若分式□运算结果为x,则在“□”中添加的运算符号为 .(请从“+、﹣、×、÷”中选择填写)
12.若m﹣=1,则m2+= .
13.小明化简分式如下:=﹣1,他的化简对还是错?(填写“对”或“错”) ,正确的化简结果是 .
14.已知,,______.
15.已知m>n>0,分式的分子分母都加上1得到分式,则分式 .(填“<、>或=”)
三.解答题
16.计算:
(1); (2);
(3)先化简再求值:(1),其中x是﹣2,1,2中的一个数值.
17.先化简:,再从2,﹣2,3,﹣3中选一个合适的数作为a的值代入求值.
18.先化简,再求值﹣,其中|x|≤1,且x为整数嘉淇同学的解法如下:
(1)请指出他解答过程中开始出现的错误的步骤是 ;
(2)写出正确的解答过程.
19.先化简,再求值:(﹣a+1)÷,其中﹣<a<且a为整数.
20.已知a2+2a﹣1=0,求下列各式的值.
(1)(a+)2
(2)a4+
(3)2a3+9a2+8a﹣2019
21.已知a为实数,且a2﹣2016a+1=0,求a2﹣2015a+的值.
答案
一.选择题
C.B.B.C.C.A.A.B.A.
二.填空题
10.3﹣x.
11.﹣或÷.
12.3.
13.错,﹣.
14.
15.>.
三.解答题
16.解:(1)
=+
=
=1;
(2)
=﹣×
=﹣
=
=;
(3)(1)
=×
=x﹣1,
∵x+2≠0,x﹣1≠0,
∴x≠﹣2,x≠1,
当x=2时,原式=2﹣1=1.
17.解:原式=÷(﹣)
=
=﹣,
∵a﹣2≠0,a﹣3≠0,a+3≠0,
∴a≠2,a≠±3,
∴当a=﹣2时,原式=﹣=﹣.
18.解:(1)开始出现的错误的步骤是②;
故答案为:②;
(2)原式=﹣=﹣==﹣.
19.解:原式=[﹣]
=
=﹣,
由﹣<a<且a为整数,得到a=﹣1,0,1,2,
当a=﹣1时,原式没有意义,舍去;
当a=0时,原式=1;
当a=1时,原式=;
当a=2时,原式=0.
20.解:(1)∵a2+2a﹣1=0,
∴a+2﹣=0,
∴a﹣=2,
∴(a﹣)2=4,
∴=4,
∴=8,
∴(a+)2=8;
(2)由(1)知(a+)2=8,
则=6,
∴=36,
∴=36,
∴=34;
(3)∵a2+2a﹣1=0,
∴a2+2a=1,
∴2a3+9a2+8a﹣2019
=2a(a2+2a)+5(a2+2a)﹣2a﹣2019
=2a×1+5×1﹣2a﹣2019
=2a+5﹣2a﹣2019
=﹣2014.
21.解:∵a2﹣2016a+1=0,
∴a2﹣2016a=﹣1,a2+1=2016a,a+=2016,
a2﹣2015a+
=a2﹣2016a+a+
=﹣1+a+
=﹣1+a+
=﹣1+2016
=2015.
一.选择题
1.与的最简公分母是( )
A.a(a+b) B.a(a﹣b)
C.a(a+b)(a﹣b) D.a2(a+b)(a﹣b)
2.把,通分,下列计算正确是( )
A.=,=
B.=,=
C.=,=
D.=,=
3.化简的结果为( )
A.a﹣b B.a+b C. D.
4.计算(1﹣)(m+1)的结果是( )
A.1 B.﹣1 C.m D.﹣m
5.如果m﹣n=1,那么代数式的值为( )
A.﹣3 B.﹣1 C.1 D.3
6.如果x2+2x﹣2=0,那么代数式 ﹣的值为( )
A.﹣2 B.﹣1 C.1 D.2
7.已知实数a,b为方程x2﹣6x+4=0的解,且a≠b,则+的值是( )
A.7 B.﹣7 C.11 D.﹣11
8.已知分式A=,B=+,其中x≠±2,则A与B的关系是( )
A.A=B B.A=﹣B C.A>B D.A<B
9.x为整数,且的值也为整数,那么符合条件的x的个数为( )
A.4个 B.3个 C.2个 D.1个
二.填空题
10.化简:= .
11.若分式□运算结果为x,则在“□”中添加的运算符号为 .(请从“+、﹣、×、÷”中选择填写)
12.若m﹣=1,则m2+= .
13.小明化简分式如下:=﹣1,他的化简对还是错?(填写“对”或“错”) ,正确的化简结果是 .
14.已知,,______.
15.已知m>n>0,分式的分子分母都加上1得到分式,则分式 .(填“<、>或=”)
三.解答题
16.计算:
(1); (2);
(3)先化简再求值:(1),其中x是﹣2,1,2中的一个数值.
17.先化简:,再从2,﹣2,3,﹣3中选一个合适的数作为a的值代入求值.
18.先化简,再求值﹣,其中|x|≤1,且x为整数嘉淇同学的解法如下:
(1)请指出他解答过程中开始出现的错误的步骤是 ;
(2)写出正确的解答过程.
19.先化简,再求值:(﹣a+1)÷,其中﹣<a<且a为整数.
20.已知a2+2a﹣1=0,求下列各式的值.
(1)(a+)2
(2)a4+
(3)2a3+9a2+8a﹣2019
21.已知a为实数,且a2﹣2016a+1=0,求a2﹣2015a+的值.
答案
一.选择题
C.B.B.C.C.A.A.B.A.
二.填空题
10.3﹣x.
11.﹣或÷.
12.3.
13.错,﹣.
14.
15.>.
三.解答题
16.解:(1)
=+
=
=1;
(2)
=﹣×
=﹣
=
=;
(3)(1)
=×
=x﹣1,
∵x+2≠0,x﹣1≠0,
∴x≠﹣2,x≠1,
当x=2时,原式=2﹣1=1.
17.解:原式=÷(﹣)
=
=﹣,
∵a﹣2≠0,a﹣3≠0,a+3≠0,
∴a≠2,a≠±3,
∴当a=﹣2时,原式=﹣=﹣.
18.解:(1)开始出现的错误的步骤是②;
故答案为:②;
(2)原式=﹣=﹣==﹣.
19.解:原式=[﹣]
=
=﹣,
由﹣<a<且a为整数,得到a=﹣1,0,1,2,
当a=﹣1时,原式没有意义,舍去;
当a=0时,原式=1;
当a=1时,原式=;
当a=2时,原式=0.
20.解:(1)∵a2+2a﹣1=0,
∴a+2﹣=0,
∴a﹣=2,
∴(a﹣)2=4,
∴=4,
∴=8,
∴(a+)2=8;
(2)由(1)知(a+)2=8,
则=6,
∴=36,
∴=36,
∴=34;
(3)∵a2+2a﹣1=0,
∴a2+2a=1,
∴2a3+9a2+8a﹣2019
=2a(a2+2a)+5(a2+2a)﹣2a﹣2019
=2a×1+5×1﹣2a﹣2019
=2a+5﹣2a﹣2019
=﹣2014.
21.解:∵a2﹣2016a+1=0,
∴a2﹣2016a=﹣1,a2+1=2016a,a+=2016,
a2﹣2015a+
=a2﹣2016a+a+
=﹣1+a+
=﹣1+a+
=﹣1+2016
=2015.
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
