第七章分式期末复习

课件28张PPT。第七章 分式复习(1)根据规律可知第5个数应是 ,(2)可知第n个数应是 (n为正整数)分式的特征:①表示两个整式相除，
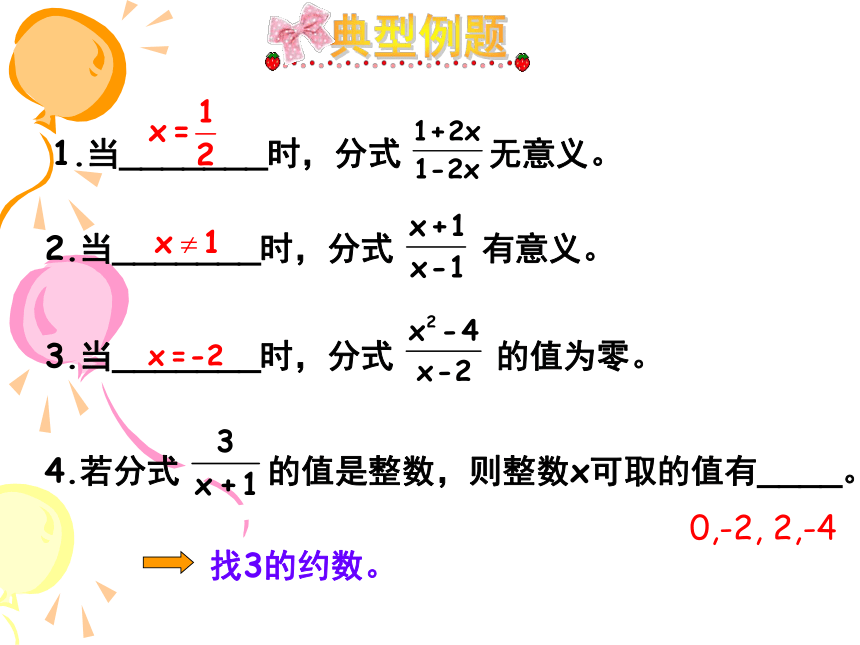
　　　 　　②除式中要含有字母．基础回顾 分式有意义的条件:B≠0 分式无意义的条件:B = 0 分式值为 0 的条件:A = 0 且 B ≠0知识梳理典型例题0,-2, 2,-4练习巩固32x≠3x=3(6)无论x取任何实数，下列分式一定有意义的是( )练习巩固(4)当x=2时,分式 没有意义,则 b=______ -4(5) 已知分式当_______________时,分式有意义;
当_______________时,分式的值是零;D知识梳理典型例题应用一分子、分母系数化整.应用二最高次项的系数都化为正数.应用三化简分式.1.不改变分式的值，把下列各式的分子与分母中各项的系数都化为整数：典型例题2.不改变分式的值，把下列分式的分子与分母的最高次项的系数都化为正数。3.化简下列分式：典型例题不变是原来的2倍CC3.如果把分式 中的x，y扩大为本身的3倍，那么
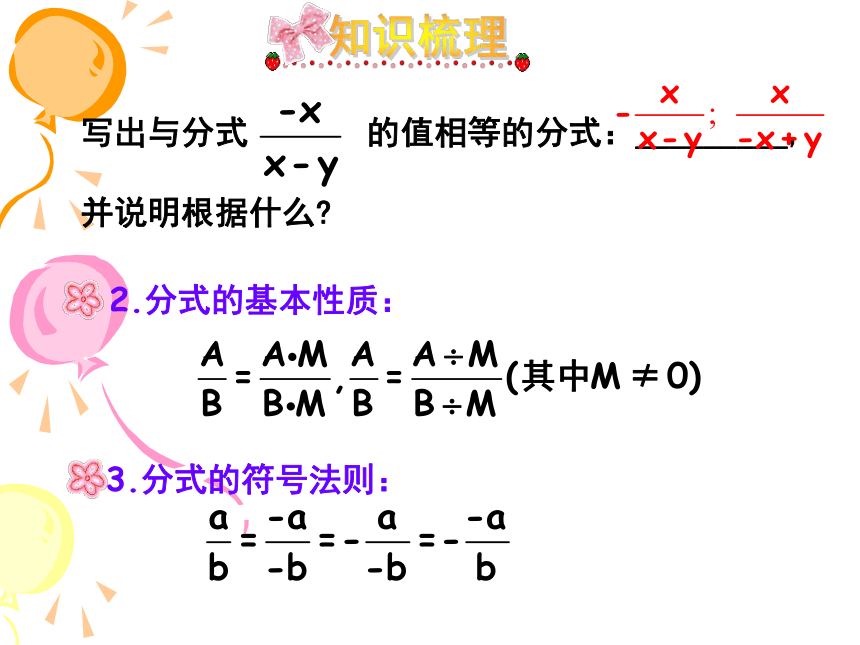
新得到的分式是原来的______倍。3练习巩固练习巩固DC知识梳理约分的关键：确定分子和分母的公因式。
通分的关键：找到最简公分母。知识梳理1.同分母分式相加减:2.异分母分式加减步骤：
(1)、找公分母；
(2)、通分；
(3)、转化为同分母加减的法则计算并化简
(确定公分母的方法:一般取各分母系数的最小公倍数与各分母各个因式的最高次幂的积为公分母)典型例题错1.计算：(1)解：原式2.化简：(2)解：原式(2)解：原式乘除为同级运算，运算顺序从左到右3.请将下面的代数式尽可能化简,再选择一个你喜欢的
数代入求值:典型例题3.请将下面的代数式尽可能化简,再选择一个你喜欢的
数代入求值:典型例题1．计算： ＝　　　　　．2.分式 的最简公分母是
_______________1练习巩固3．计算： =_______练习巩固4．“一课一练”P75(19)题 计算：知识梳理三步骤：两边同乘各分式的最简公分母。
解整式方程。
检验。关键：仔细分析各种量之间的关系，灵活设
未知数；找等量关系。
注意：两个检验。经检验,分式方程必须检验,若有增根,要舍去找出公分母典型例题1.解方程：解：方程两边同乘以(x+1)(x-1)，得解 去分母，得当x=2时，所以，当m为-4时,去分母解方程会产生增根.典型例题1、下列方程中，是分式方程（ ）C练习巩固2、“一课一练”P75(20)题 解方程：数学模型(分式,分式方程)利润＝销售价－成本价
销售价＝成本价（１＋利润率）
总价＝单价×数量
工作量＝工作时间×效率，常把工作量看作１
顺流速度＝静水速度＋水速
　逆流速度＝静水速度－水速常见数量关系知识梳理典型例题1.一项工程，需要在规定日期内完成，如果甲队独做，恰好如期完成，如果乙队独做，就要超过规定3天，现在由甲、乙两队合作2天，剩下的由乙队独做，也刚好在规定日期内完成， 问规定日期是几天？2.某人骑自行车比步行每小时多走8千米，如果他步行12千米所用时间与骑车行36千米所用的时间相等，求他步行的速度是多少千米/小时？
典型例题3.为响应承办绿色奥运的号召，某班组织部分同学义务植树180棵。由于同学们积极参加，实际参加植树的人数比原计划增加了50%，结果没人比原计划少栽了2棵树。
问实际有多少人参加这次植树活动？解：去分母得：yz=xz+xy
移项得：yz-xz=xy
合并同类项得：（y-x)z=xy
∵x≠y ∴y-x≠0

∴典型例题(2)已知 ;先化简,再求值:
(1)其中 ;(3)已知 .拓展与提高