第1章 平行线单元检测卷（含解析）

中小学教育资源及组卷应用平台
2024年浙教版七年级下册第1章《平行线》单元检测卷
一．选择题（共10小题，满分30分，每小题3分）
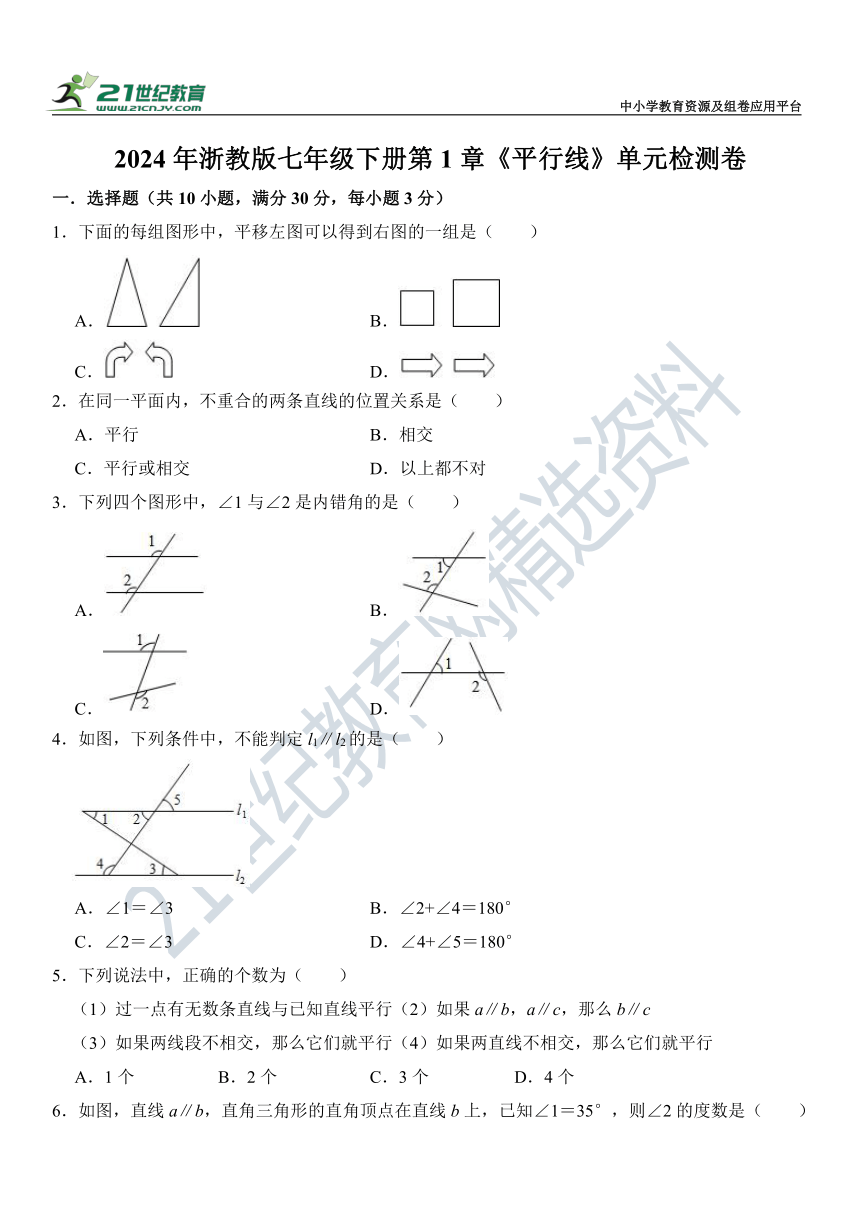
1．下面的每组图形中，平移左图可以得到右图的一组是（　　）
A． B．
C． D．
2．在同一平面内，不重合的两条直线的位置关系是（　　）
A．平行 B．相交
C．平行或相交 D．以上都不对
3．下列四个图形中，∠1与∠2是内错角的是（　　）
A． B．
C． D．
4．如图，下列条件中，不能判定l1∥l2的是（　　）
A．∠1＝∠3 B．∠2+∠4＝180°
C．∠2＝∠3 D．∠4+∠5＝180°
5．下列说法中，正确的个数为（　　）
（1）过一点有无数条直线与已知直线平行（2）如果a∥b，a∥c，那么b∥c
（3）如果两线段不相交，那么它们就平行（4）如果两直线不相交，那么它们就平行
A．1个 B．2个 C．3个 D．4个
6．如图，直线a∥b，直角三角形的直角顶点在直线b上，已知∠1＝35°，则∠2的度数是（　　）
A．35° B．45° C．55° D．65°
7．如图，△ABC平移到△DEF的位置，则下列结论错误的是（　　）
A．AD∥BE B．BC∥EF C．∠ABE＝∠DEF D．∠ACB＝∠DFE
8．生活中的椅子一般依据人体工学原理设计，如图为生活中一把椅子的侧面图，从人体脊柱的形势而言，当靠背角度∠DEF＝115°时，能产生较为接近自然腰部的形状，此时最舒适．已知DE与地面平行，支撑杆BD与地面夹角∠ABD＝50°，则制作时用螺丝固定时支撑杆BD和AF需构成夹角∠ACB为（　　）
A．70° B．65° C．60° D．50°
9．车库的电动门栏杆如图所示，BA垂直于地面AE于A，CD平行于地面AE，则∠ABC+∠BCD的大小是（　　）
A．150° B．180° C．270° D．360°
10．如图，AB∥EF，∠C＝60°，则α，β，γ的关系为（　　）
A．β＝α+γ B．α+β﹣γ＝60°
C．β+γ﹣α＝90° D．α+β+γ＝180°
二．填空题（共5小题，满分15分，每小题3分）
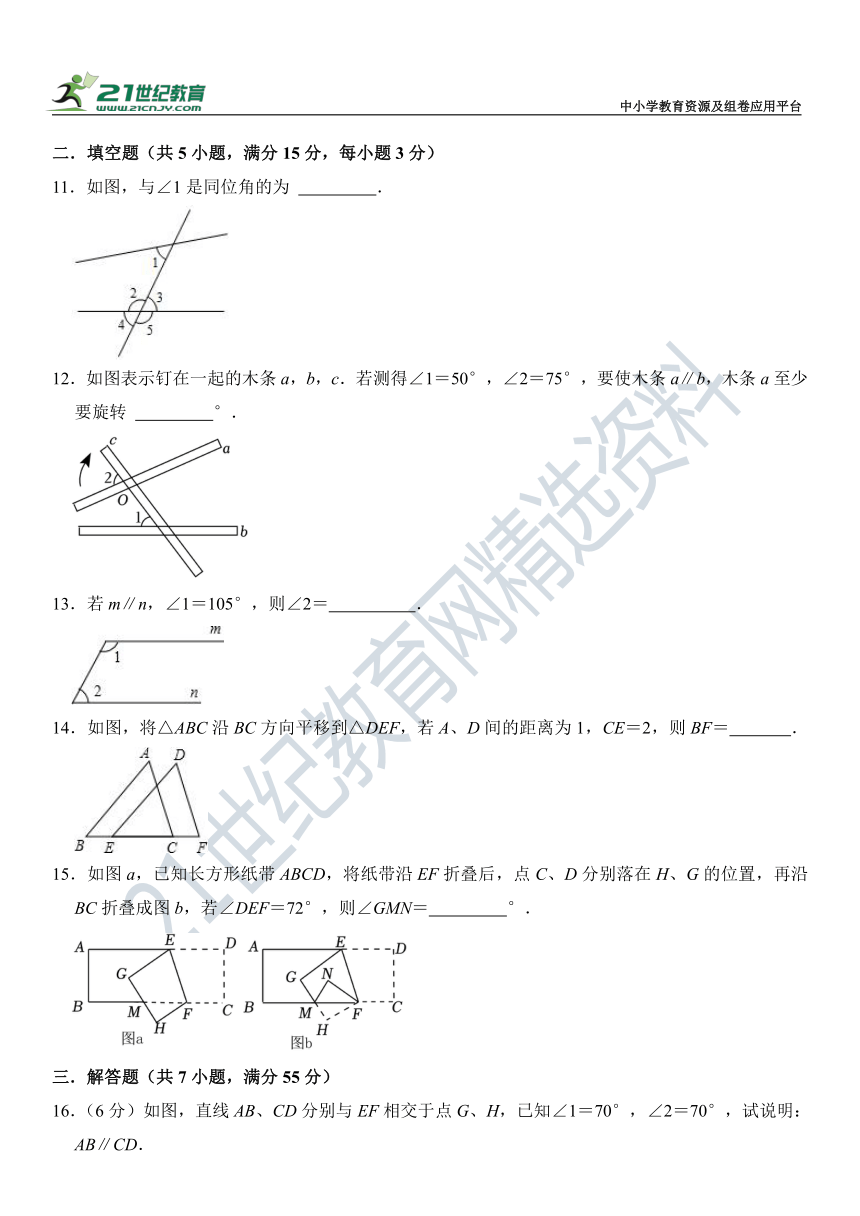
11．如图，与∠1是同位角的为 　 　．
12．如图表示钉在一起的木条a，b，c．若测得∠1＝50°，∠2＝75°，要使木条a∥b，木条a至少要旋转 　 　°．
13．若m∥n，∠1＝105°，则∠2＝　 　．
14．如图，将△ABC沿BC方向平移到△DEF，若A、D间的距离为1，CE＝2，则BF＝　 　．
15．如图a，已知长方形纸带ABCD，将纸带沿EF折叠后，点C、D分别落在H、G的位置，再沿BC折叠成图b，若∠DEF＝72°，则∠GMN＝　 　°．
三．解答题（共7小题，满分55分）
16．（6分）如图，直线AB、CD分别与EF相交于点G、H，已知∠1＝70°，∠2＝70°，试说明：AB∥CD．
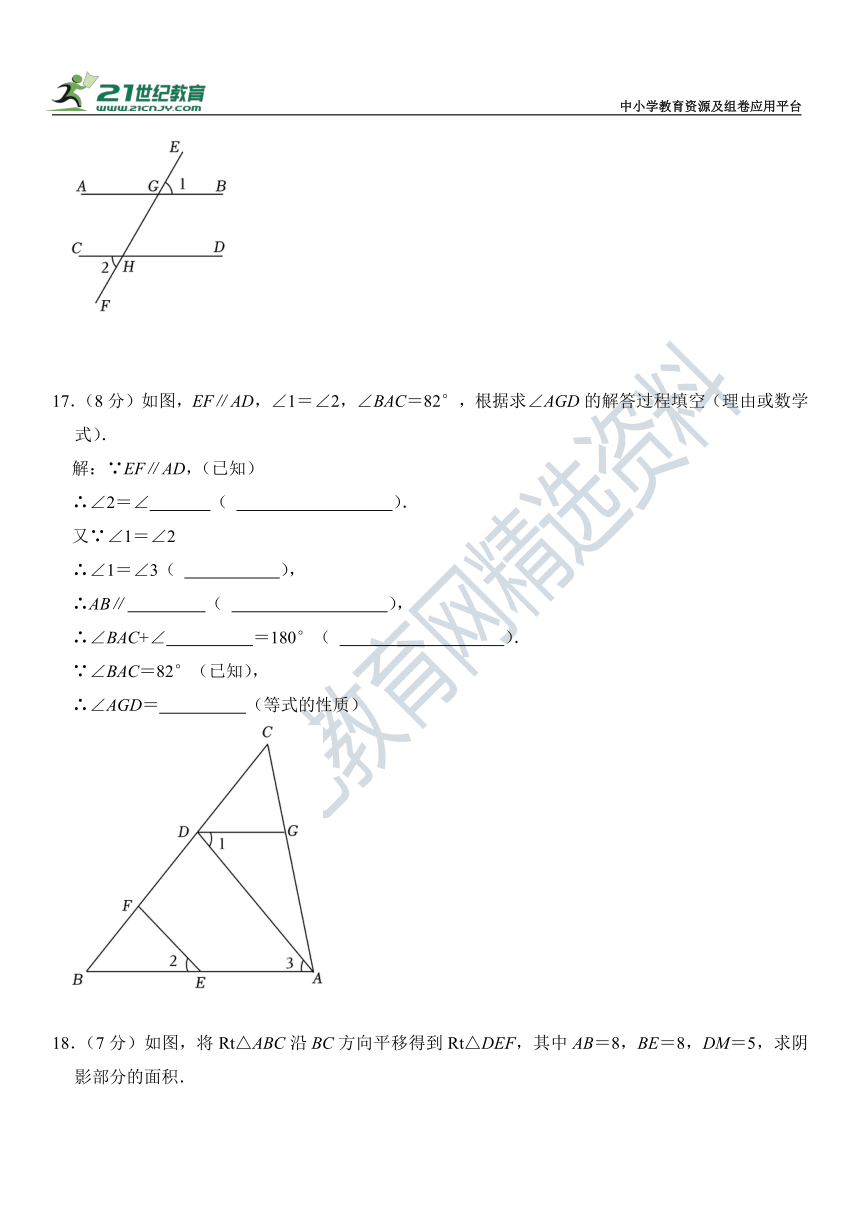
17．（8分）如图，EF∥AD，∠1＝∠2，∠BAC＝82°，根据求∠AGD的解答过程填空（理由或数学式）．
解：∵EF∥AD，（已知）
∴∠2＝∠　 　（ 　 　）．
又∵∠1＝∠2
∴∠1＝∠3（ 　 　），
∴AB∥　 　（ 　 　），
∴∠BAC+∠　 　＝180°（ 　 　）．
∵∠BAC＝82°（已知），
∴∠AGD＝　 　（等式的性质）
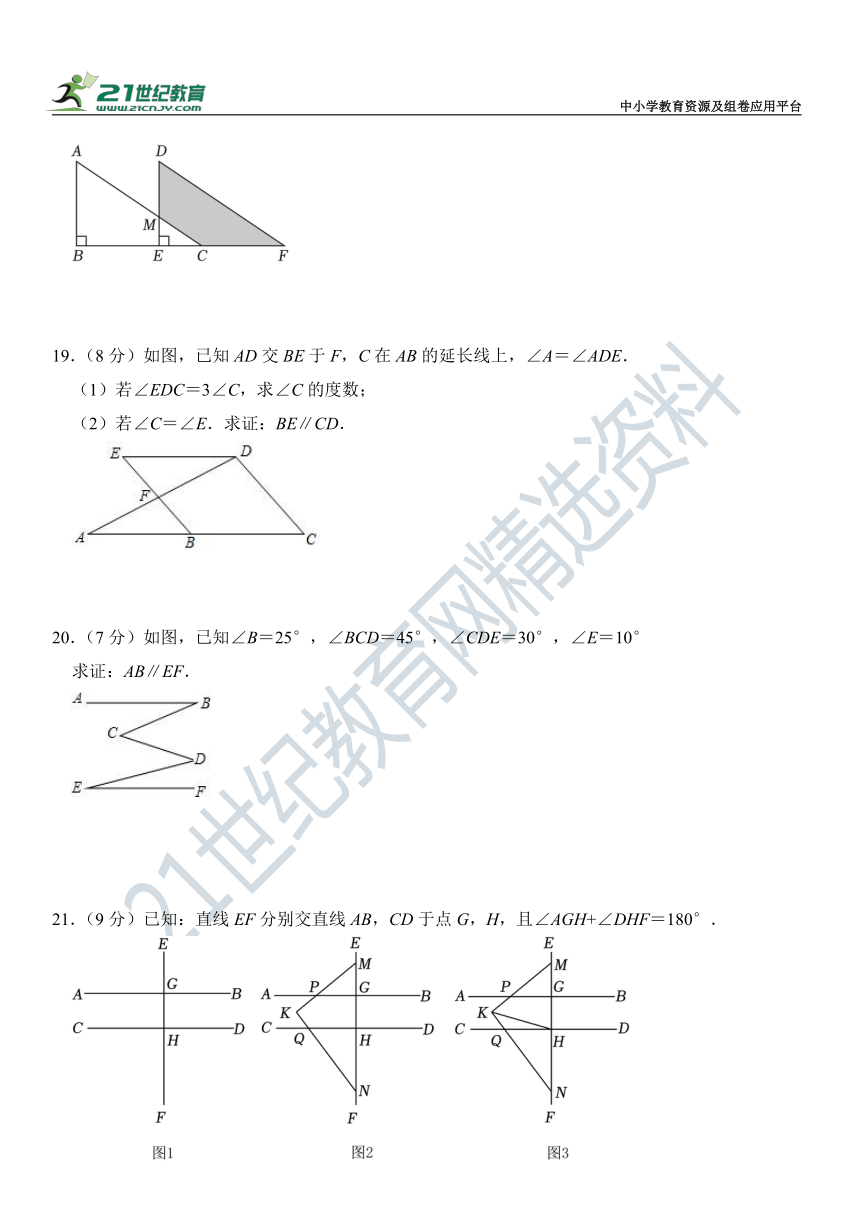
18．（7分）如图，将Rt△ABC沿BC方向平移得到Rt△DEF，其中AB＝8，BE＝8，DM＝5，求阴影部分的面积．
19．（8分）如图，已知AD交BE于F，C在AB的延长线上，∠A＝∠ADE．
（1）若∠EDC＝3∠C，求∠C的度数；
（2）若∠C＝∠E．求证：BE∥CD．
20．（7分）如图，已知∠B＝25°，∠BCD＝45°，∠CDE＝30°，∠E＝10°
求证：AB∥EF．
21．（9分）已知：直线EF分别交直线AB，CD于点G，H，且∠AGH+∠DHF＝180°．
（1）如图1，求证：AB∥CD；
（2）如图2，点M，N分别在射线GE，HF上，点P，Q分别在射线GA，HC上，连接MP，NQ，且∠MPG+∠NQH＝90°，分别延长MP，NQ交于点K，求证：MK⊥NK；
（3）如图3，在（2）的条件下，连接KH，KH平分∠MKN，且HE平分∠KHD，若，求∠KMN的度数．
22．（10分）已知直线AM∥BN，点P是直线AM上的一个动点（不与点A重合），BC平分∠PBN，交直线AM于点C．
（1）如图1，当点P在点A左侧时，若∠CPB＝40°，请直接写出∠PCB的度数，不必说明理由；
（2）若∠MAB＝60°，BD平分∠PBA，交直线AM于点D．
①如图2，若点P在点A左侧运动时，∠DBC的度数是否会发生变化？若不变，求出该度数；若变化，请说明理由；
②∠ADB与∠ABC之间存在怎样的数量关系？请写出结论，并说明理由．
2024年浙教版七年级下册第1章《平行线》单元检测卷
参考答案与试题解析
一．选择题（共10小题，满分30分，每小题3分）
1．【解答】解：A、左图与右图的形状不同，所以A选项错误；
B、左图与右图的大小不同，所以B选项错误；
C、左图通过翻折得到右图，所以C选项错误；
D、左图通过平移可得到右图，所以D选项正确．
故选：D．
2．【解答】解：在同一平面内，不重合的两条直线只有两种位置关系，是平行或相交，
所以在同一平面内，不重合的两条直线的位置关系是：平行或相交．
故选：C．
3．【解答】解：A、∠1与∠2是同位角，选项错误，不符合题意；
B、∠1与∠2是同旁内角，选项错误，不符合题意；
C、∠1与∠2不是内错角，选项错误，不符合题意；
D、∠1与∠2是内错角，选项正确，符合题意；
故选：D．
4．【解答】解：A、∵∠1＝∠3，
∴直线l1∥l2，故此选项不合题意；
B、∵∠2+∠4＝180°，
∴直线l1∥l2，故此选项不合题意；
C、∠2＝∠3，不能得出直线l1∥l2，故此选项符合题意；
D、∵∠2＝∠5，∠4+∠5＝180°，
∴∠4+∠2＝180°，
∴直线l1∥l2，故此选项不合题意．
故选：C．
5．【解答】解：（1）过直线外一点有且只有一条直线与已知直线平行，故错误；
（2）根据平行公理的推论，正确；
（3）线段的长度是有限的，不相交也不一定平行，故错误；
（4）应该是“在同一平面内”，故错误．
正确的只有一个，故选A．
6．【解答】解：∵直线a∥b，∠1＝35°，
∴∠3＝∠1＝35°，
∵直角三角形的直角顶点在直线b上，
∴∠2＝180°﹣90°﹣35°＝55°．
故选：C．
7．【解答】解：A、AD与BE是对应边，∴AD∥DE，正确；
B、BC与EF是对应边，∴BC∥EF，正确；
C、∵∠ABC＝∠DEF，∴∠ABE≠∠DEF，故本选项错误；
D、∠ACB与∠DFE是对应角，∴∠ACB＝∠DFE，正确．
故选：C．
8．【解答】解：∵∠DEF＝115°，
∴∠DEC＝180°﹣∠DEF＝65°，
∵DE∥AB，
∴∠CAB＝∠DEC＝65°，
∵∠ABD＝50°，
∴∠ACB＝180°﹣∠ABD﹣∠CAB＝65°．
故选：B．
9．【解答】解：过点B作BF∥AE，如图，
∵CD∥AE，
∴BF∥CD，
∴∠BCD+∠CBF＝180°，
∵AB⊥AE，
∴AB⊥BF，
∴∠ABF＝90°，
∠ABC+∠BCD＝∠ABF+∠CBF+∠BCD＝90°+180°＝270°．
故选：C．
10．【解答】解：延长DC交AB与G，延长CD交EF于H．
在△BGC中，∠1＝60°﹣α，
∵∠β＝∠2+∠γ，
∴∠2＝β﹣γ，
∵AB∥EF，
∴∠1＝∠2，
∴60°﹣α＝β﹣γ，即α+β﹣γ＝60°．
故选：B．
二．填空题（共5小题，满分15分，每小题3分）
11．【解答】解：如图，与∠1是同位角的为：∠4，
故答案为：∠4．
12．【解答】解：如图，
∵∠AOC＝∠1＝50°时，AB∥b，
∴要使木条a与b平行，木条a旋转的度数至少是75°﹣50°＝25°．
故答案为：25．
13．【解答】解：∵m∥n，∠1＝105°，
∴∠2＝180°﹣∠1＝180°﹣105°＝75°．
故答案为：75°．
14．【解答】解：观察图形可知：将△ABC沿BC方向平移到△DEF，根据对应点连接的线段平行且相等，得BE＝CF＝AD＝1．
∴BF＝BE+EC+CF＝4．
15．【解答】解：∵AD∥CB，
∴∠EFC+∠DEF＝180°，∠EFB＝∠DEF，
即∠EFC＝180°﹣72°＝108°，∠EFB＝72°，
∴∠BFH＝108°﹣72°＝36°．
∵∠H＝∠D＝90°，
∴∠HMF＝180°﹣90°﹣36°＝54°．
由折叠可得：∠NMF＝∠HMF＝54°，
∴∠GMN＝72°．
故答案为：72．
三．解答题（共7小题，满分55分）
16．【解答】解：∵∠1＝∠AGH，∠1＝∠2＝70°，
∴∠2＝∠AGH，
∴AB∥CD．
17．【解答】解：∵EF∥AD，（已知）
∴∠2＝∠3（两直线平行，同位角相等）．
又∵∠1＝∠2
∴∠1＝∠3（等量代换），
∴AB∥DG（内错角相等，两直线平行），
∴∠BAC+∠AGD＝180°（两直线平行，同旁内角互补）．
∵∠BAC＝82°（已知），
∴∠AGD＝98°（等式的性质）
故答案为：3；两直线平行，同位角相等；等量代换；DG；内错角相等，两直线平行；AGD；两直线平行，同旁内角互补；98°．
18．【解答】解：∵直角△ABC沿BC方向平移得到直角△DEF，
∴DE＝AB＝8，
∵DM＝5，
∴ME＝DE﹣DM＝8﹣5＝3，
由平移可得：
S阴影＝S△DEF﹣S△MEC
＝S△ABC﹣S△MEC
＝S梯形ABEM
＝×（3+8）×8，
＝44．
19．【解答】解：（1）∵∠A＝∠ADE，
∴AC∥DE，
∴∠EDC+∠C＝180°，
又∵∠EDC＝3∠C，
∴4∠C＝180°，
即∠C＝45°；
（2）∵AC∥DE，
∴∠E＝∠ABE，
又∵∠C＝∠E，
∴∠C＝∠ABE，
∴BE∥CD．
20．【解答】解：过C点作CG∥AB，过点D作DH∥AB，则CG∥DH，
∵∠B＝25°，
∴∠BCG＝25°，
∵∠BCD＝45°，
∴∠GCD＝20°，
∵CG∥HD，
∴∠CDH＝20°，
∵∠CDE＝30°，
∴∠HDE＝10°
∴∠HDE＝∠E＝10°，
∴DH∥EF，
∴DH∥AB，
∴AB∥EF．
21．【解答】（1）证明：∵∠CHG＝∠DHF，∠AGH+∠DHF＝180°，
∴∠AGH+∠CHG＝180°，
∴AB∥CD；
（2）证明：过K作KR∥AB，如图，
∵AB∥CD，
∴RK∥AB∥CD，
∴∠MPG＝∠MKR，∠NQH＝∠RKN，
∵∠MPG+∠NQH＝90°，
∴∠MKR+∠NKR＝90°
∴∠MKN＝90°，
∴MK⊥NK；
（3）解：如图，过M作MT∥AB，过K作KR∥AB，
∵AB∥CD，
∴MT∥AB∥CD∥KR，
∵KH平分∠MKN，
∴∠MKH＝∠NKH＝45°
∵，
∴设∠DHG＝17x，∠MPG＝7x，
∵HE平分∠KHD，
∴∠KHM＝∠DHG＝17x，
∴∠KHD＝34x∴∠KHQ＝180°﹣34x，
∵CD∥KR，
∴∠RKH＝∠KHQ＝180°﹣34x，
∵MT∥AB∥KR
∴∠TMP＝∠MKR＝∠MPG＝7x，∠TMH＝∠MHD＝17x，
∵∠MKH＝45°，
∴∠RKH+∠MKR＝180°﹣34x+7x＝45°，
∴x＝5°，
∵∠KMN＝∠TMH﹣∠TMP，
∴∠KMN＝17x﹣7x＝10x＝50°．
22．【解答】解：（1）延长NB到E，如图1所示：
∵AM∥BN，∠CPB＝40°，
∴∠PBE＝∠CPB＝40°，
∴∠PBN＝180°﹣∠PBE＝140°，
∵BC平分∠PBN，
∴∠CBN＝∠PBN＝70°，
∵AM∥BN，
∴∠PCB＝∠CBN＝70°；
（2）①点P在点A左侧运动时，∠DBC的度数不发生变化，∠DBC＝60°，理由如下：
延长NB到E，如图2所示：
设∠ABD＝α，
∵BD平分∠PBA，
∴∠PBD＝∠ABD＝α，∠ABP＝2α，
∵AM∥BN，∠MAB＝60°，
∴∠EBA＝∠MAB＝60°，
∴∠EBP＝∠EBA﹣∠ABP＝60°﹣2α，
∴∠PBN＝180°﹣∠EBP＝180°﹣（60°﹣2α）＝120°+2α，
∵BC平分∠PBN，
∴∠PBC＝∠PBN＝（120°+2α）＝60°+α，
∴∠DBC＝∠PBC﹣∠PBD＝60°+α﹣α＝60°，
②∠ADB与∠ABC之间的数量关系是：∠ADB＝∠ABC或∠ADB+∠ABC＝180°，理由如下：
（ⅰ）当点P在点A的左侧时，延长NB到E，如图3所示：
设∠ABD＝α，
∵BD平分∠PBA，
∴∠PBD＝∠ABD＝α，∠ABP＝2α，
∵AM∥BN，∠MAB＝60°，
∴∠EBA＝∠MAB＝60°，
∴∠ADB＝∠EBD＝∠EBA﹣∠ABD＝60°﹣α，
∵∠EBP＝∠EBA﹣∠ABP＝60°﹣2α，
∴∠PBN＝180°﹣∠EBP＝180°﹣（60°﹣2α）＝120°+2α，
∵BC平分∠PBN，
∴∠PBC＝∠PBN＝（120°+2α）＝60°+α，
∴∠ACB＝∠PBC﹣∠ABP＝60°+α﹣2α＝60°﹣α，
∴∠ADB＝∠ACB；
（ⅱ）当点P在点A的右侧时，延长NB到E，如图4所示：
设∠ABD＝α，
∵BD平分∠PBA，
∴∠PBD＝∠ABD＝α，∠ABP＝2α，
∵AM∥BN，∠MAB＝60°，
∴∠EBA＝∠MAB＝60°，
∴∠EBD＝∠EBA+∠ABD＝60°+α，
∵AM∥BN，
∴∠ADB+∠EBD＝180°，
∴∠ADB＝180°﹣∠EBD＝180°﹣（60°+α）＝120°﹣α，
∵∠EBA＝∠MAB＝60°，∠ABP＝2α，
∴∠EBP＝∠EBA+∠ABP＝60°+2α，
∴∠PBN＝180°﹣∠EBP＝180°﹣（60°+2α）＝120°﹣2α，
∵BC平分∠PBN，
∴∠PBC＝∠PBN＝（120°﹣2α）＝60°﹣α，
∴∠ABC＝∠ABP+∠PBC＝2α+60°﹣α＝60°+α，
∴∠ADB+∠ABC＝120°﹣α+60°+α＝180°．
综上所述：∠ADB与∠ABC之间的数量关系是：∠ADB＝∠ABC或∠ADB+∠ABC＝180°．