第1章《平行线》单元达标检测试卷 (含解析)
文档属性
| 名称 | 第1章《平行线》单元达标检测试卷 (含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-18 12:09:57 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
浙教版七年级数学下册第1章《平行线》单元达标检测试卷 (含解析)
选择题(本大题共有10个小题,每小题4分,共40分)
1.如图,与构成同位角的是( )
A. B. C. D.
2 . 如图,,要使,则的度数是( )
A. B. C. D.
3.如图,将直尺与含角的三角尺叠放在一起.若,则的大小是( )
A. B. C. D.
4 . 如图,下列条件中,不能判断的是( )
A. B. C. D.
5 . 如图是6级台阶侧面的示意图,如果要在台阶上铺地毯,台阶宽为2米,
那么至少要买地毯( )平方米.
A.8 B.15 C.16 D.30
6 . 如下图,下列条件中:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5,
能判定ABCD的条件为( )
A.①②③④ B.①②④ C.①③④ D.①②③
7.如图AB//CD,若∠B=120°,∠C=25°则∠1=( )
A.75° B.80° C.85° D.95°
8 .如图,AB∥CD,直线EF交AB于点E,交CD于点F,EG平分∠BEF,交CD于点G,
若∠1=50°,则∠2等于( )
A.50° B.60° C.65° D.90°
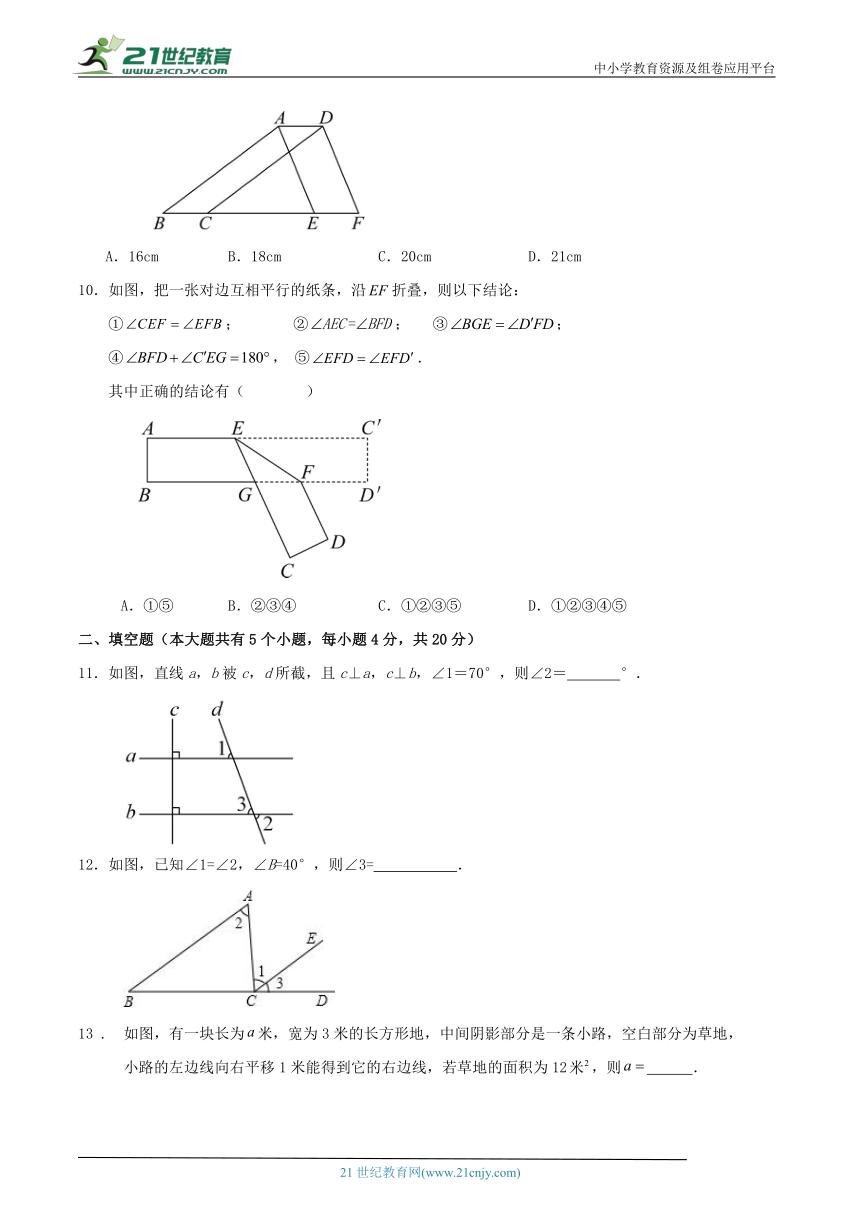
9 .如图,将△ABE向右平移2cm得到△DCF,如果△ABE的周长是16cm,
那么四边形ABFD的周长是( )
A.16cm B.18cm C.20cm D.21cm
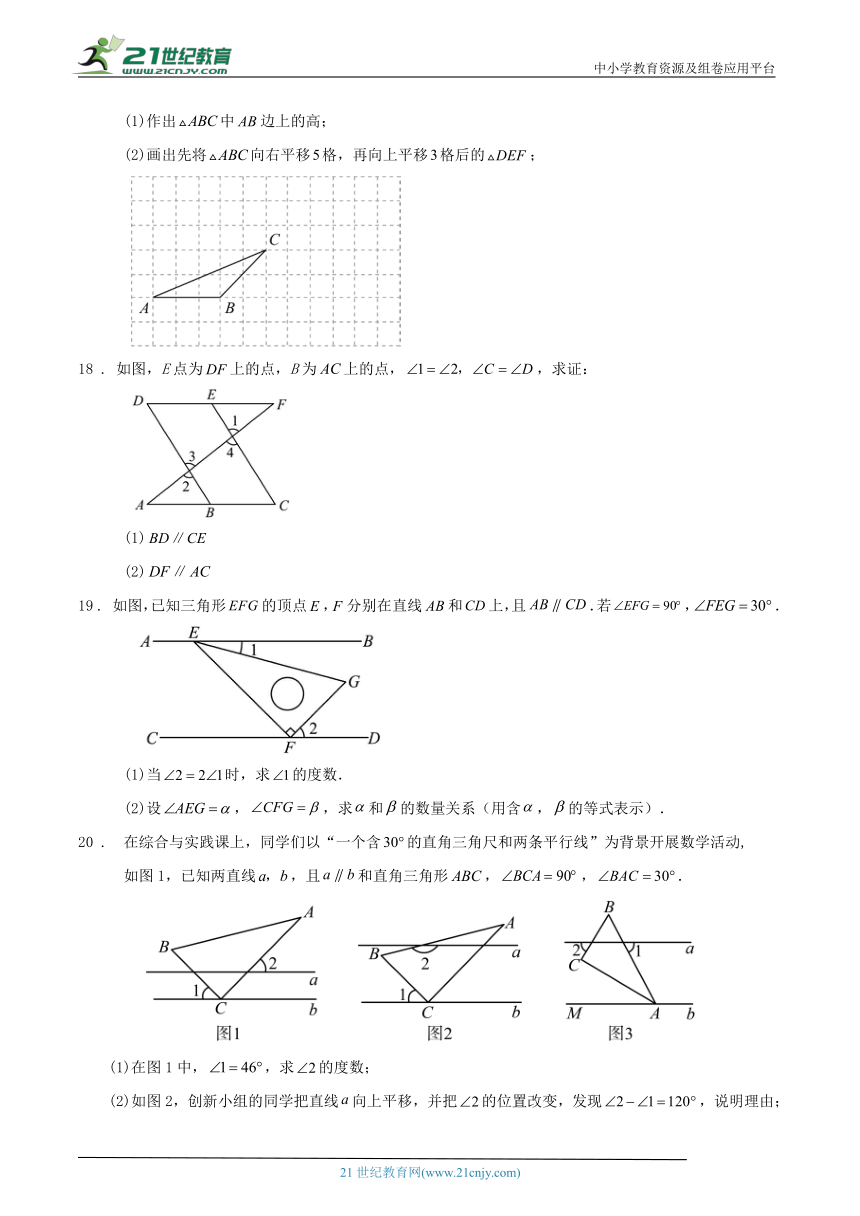
如图,把一张对边互相平行的纸条,沿折叠,则以下结论:
①; ②; ③;
④, ⑤.
其中正确的结论有( )
A.①⑤ B.②③④ C.①②③⑤ D.①②③④⑤
填空题(本大题共有5个小题,每小题4分,共20分)
11.如图,直线a,b被c,d所截,且c⊥a,c⊥b,∠1=70°,则∠2= °.
12.如图,已知∠1=∠2,∠B=40°,则∠3= .
13 . 如图,有一块长为米,宽为3米的长方形地,中间阴影部分是一条小路,空白部分为草地,
小路的左边线向右平移1米能得到它的右边线,若草地的面积为12,则 .
如图所示,C岛在A岛的北偏东50°方向,C岛在B岛的北偏西40°方向,
则从C岛看A、B两岛的视角∠ACB等于 .
15.如图,把长方形ABCD沿EF对折,若∠1=50°,则∠AEF的度数等于 .
解答题(本大题共有5个小题,共40分)
16 . 已知:如图,直线a,b,c被直线l所截,,.求证:.
17 . 如图:在正方形网格中有一个,按要求进行下列作图(只能借助于网格):
(1)作出中边上的高;
(2)画出先将向右平移格,再向上平移格后的;
18 . 如图,E点为上的点,B为上的点,,求证:
(1)
(2)
19 . 如图,已知三角形的顶点,分别在直线和上,且.若,.
(1)当时,求的度数.
(2)设,,求和的数量关系(用含,的等式表示).
20 . 在综合与实践课上,同学们以“一个含的直角三角尺和两条平行线”为背景开展数学活动,
如图1,已知两直线,且和直角三角形,,.
(1)在图1中,,求的度数;
(2)如图2,创新小组的同学把直线向上平移,并把的位置改变,发现,说明理由;
(3)竞赛小组在创新小组发现结论的基础上,将图2中的图形继续变化得到图3,
当平分时,此时发现与又存在新的数量关系,
请写出与的数量关系并证明.
浙教版七年级数学下册第1章《平行线》单元达标检测试卷 解析
一、选择题(本大题共有10个小题,每小题4分,共40分)
1.如图,与构成同位角的是( )
A. B. C. D.
【答案】C
【分析】本题主要考查了同位角,同位角的边构成“F“形,内错角的边构成“Z“形,同旁内角的边构成“U”形.两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角.
【详解】解:直线a,b被直线m所截,与构成同位角的是,
故选:C.
2 . 如图,,要使,则的度数是( )
A. B. C. D.
【答案】D
3.如图,将直尺与含角的三角尺叠放在一起.若,则的大小是( )
A. B. C. D.
【答案】B
【分析】本题考查了平行线的性质及直角三角形的性质,充分运用三角板和直尺的几何特征是解题的关键.由三角尺可知,由平角可求,再根据平行线的性质可知.
【详解】解:如图:
由三角尺可知,
∵,
∴,
由平行线的性质可知.
故选:B.
4 . 如图,下列条件中,不能判断的是( )
A. B. C. D.
【答案】D
【分析】本题考查了平行线的判定,结合图形分析两角的位置关系,根据平行线的判定方法逐项判断即可,解题的关键是熟练掌握两直线平行的判定方法.
【详解】、由,根据内错角相等,两直线平行,可以判断,不符合题意;
、由,根据同位角相等,两直线平行,可以判断,不符合题意;
、由,根据同旁内角互补,两直线平行,可以判断,不符合题意;
、由,不可以判断,符合题意;
故选:.
5 . 如图是6级台阶侧面的示意图,如果要在台阶上铺地毯,台阶宽为2米,
那么至少要买地毯( )平方米.
A.8 B.15 C.16 D.30
【答案】C
【分析】本题考查有关平移的性质、面积计算,将图形中较短的竖线左移,较短的横线上移,平移线段后,地毯的长度是长5米,宽3米的长方形的一组邻边长度和.地毯的面积=楼梯宽度×矩形的长.
【详解】解:(平方米),
(平方米),
∴至少要买地毯16平方米.
故选:C.
6 . 如下图,下列条件中:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5,
能判定ABCD的条件为( )
A.①②③④ B.①②④ C.①③④ D.①②③
【答案】C
【详解】解:①∵∠B+∠BCD=180°
∴ABCD
②∵∠1=∠2
∴ADBC
③∵∠3=∠4
∴ABCD
④∵∠B=∠5
∴ABCD
∴能得到ABCD的条件是①③④.
故选C.
7.如图AB//CD,若∠B=120°,∠C=25°则∠1=( )
A.75° B.80° C.85° D.95°
【答案】C
【分析】首先过点作,由,可得,利用平行线的性质,即可求得与的度数,继而求得答案.
【详解】解:过点作,
,
,,
,
故选:C.
8 .如图,AB∥CD,直线EF交AB于点E,交CD于点F,EG平分∠BEF,交CD于点G,
若∠1=50°,则∠2等于( )
A.50° B.60° C.65° D.90°
【答案】C
【详解】∵AB∥CD,
∴∠BEF+∠1=180°(两直线平行,同旁内角互补)
∵∠1=50°,
∴∠BEF=130°
∵EG平分∠BEF,
∴∠BEG=∠BEF=65°(角平分线的定义)
∴∠2=∠BEG=65°(两直线平行,内错角相等),
故选C
9 .如图,将△ABE向右平移2cm得到△DCF,如果△ABE的周长是16cm,
那么四边形ABFD的周长是( )
A.16cm B.18cm C.20cm D.21cm
【答案】C
【详解】试题分析:已知,△ABE向右平移2cm得到△DCF,
根据平移的性质得到EF=AD=2cm,AE=DF,
又因△ABE的周长为16cm,
所以AB+BC+AC=16cm,
则四边形ABFD的周长=AB+BC+CF+DF+AD=16cm+2cm+2cm=20cm.
故答案选C.
10.如图,把一张对边互相平行的纸条,沿折叠,则以下结论:①;②;③; ④, ⑤.其中正确的结论有( )
A.①⑤ B.②③④ C.①②③⑤ D.①②③④⑤
【答案】D
【分析】根据平行线的性质,以及折叠的性质即可判断①,根据平行线的性质可得,,即可判断②,根据平行线的性质可得,根据对等角相等可得,即可判断③,根据平行线的性质得出,根据邻补角的定义,即可判断④,根据折叠的性质即可判断⑤
【详解】解:∵
∴
∵折叠,
∴,
∴,故①正确;
∵
∴
又
∴
∴,故②正确
∵
∴
又
∴,故③正确
∵,,
又
∴
∴
∵
∴,故④正确;
根据折叠的性质可得,故⑤正确,
故选:D.
二、填空题(本大题共有5个小题,每小题4分,共20分)
11.如图,直线a,b被c,d所截,且c⊥a,c⊥b,∠1=70°,则∠2= °.
【答案】70
【详解】∵c⊥a,c⊥b,
∴a∥b,
∴∠1=∠3,
∵∠2=∠3,
∴∠2=∠1=70°.
故答案为:70
12.如图,已知∠1=∠2,∠B=40°,则∠3= .
【答案】40°/40度
【详解】∵∠1=∠2,
∴AB//CE,
∴∠3=∠B=40°.
故答案为40°.
13 . 如图,有一块长为米,宽为3米的长方形地,中间阴影部分是一条小路,空白部分为草地,
小路的左边线向右平移1米能得到它的右边线,若草地的面积为12,则 .
【答案】5
【分析】根据小路的左边线向右平移1米能得到它的右边线,可得路的宽度是1米,根据平移,可把路移到左边,再根据面积公式,可得答案.
【详解】解:依题意有3a-3×1=12,
解得a=5.
故答案为:5.
14 . 如图所示,C岛在A岛的北偏东50°方向,C岛在B岛的北偏西40°方向,
则从C岛看A、B两岛的视角∠ACB等于 .
【答案】90°
【分析】根据方位角的概念和平行线的性质即可得答案.
【详解】过点C作CD∥AE,
∵AE∥BF,
∴CD∥AE∥BF,
∴∠ACD=∠EAC=50°,∠BCD=∠CBF=40°,
∴∠ACB=∠ACD十∠BCD=50°+40°=90°.
故答案为90.
15.如图,把长方形ABCD沿EF对折,若∠1=50°,则∠AEF的度数等于 .
【答案】
【详解】解:∵把长方形ABCD沿EF对折,
∴AD∥BC,∠BFE=∠2,
∵∠1=50°,∠1+∠2+∠BFE=180°,
∴∠BFE==65°,
∵∠AEF+∠BFE=180°,
∴∠AEF=115°.
故答案为:115°.
三 . 解答题(本大题共有5个小题,共40分)
16 . 已知:如图,直线a,b,c被直线l所截,,.求证:.
证明:∵,
∴______(______).
∵,
∴______(______).
∴(______).
【答案】见解析
【分析】根据平行线的判定即可正确求解.
【详解】证明:∵,
∴b(同旁内角互补,两直线平行).
∵,
∴ c(同位角相等,两直线平行).
∴(如果两条直线都与第三条直线平行,那么这两条直线也互相平行).
17 . 如图:在正方形网格中有一个,按要求进行下列作图(只能借助于网格):
(1)作出中边上的高;
(2)画出先将向右平移格,再向上平移格后的;
【答案】(1)见解析
(2)见解析
【分析】(1)要作出边上的高,即过点作直线的垂线,网格中的横线与竖线互相垂直;
(2)首先找出的三个顶点按要求平移后的位置,然后顺次连接各点,即可得到.
【详解】(1)解:如图所示;即为所求;
(2)如图所示,即为所求.
完成下面的证明.
18 . 如图,E点为上的点,B为上的点,,求证:
(1)
(2)
【答案】(1)证明见解析
(2)证明见解析
【分析】(1)先由对顶角相等,得到:,然后根据等量代换得到:,然后根据同位角相等两直线平行,得到;
(2)根据两直线平行,同位角相等,得到,然后根据等量代换得到:,最后根据内错角相等两直线平行,即可得到.
【详解】(1)∵,,
∴,
∴;
(2)∵
∴,
∵,
∴,
∴.
19 . 如图,已知三角形的顶点,分别在直线和上,且.若,.
(1)当时,求的度数.
(2)设,,求和的数量关系(用含,的等式表示).
【答案】(1)
(2)
【分析】(1)根据两直线平行,同旁内角互补即可求解;
(2)过点过点作,可得,根据两直线平行,同旁内角互补得到,,由此得到,在中,,由此即可求解.
【详解】(1)解:∵,
∴,即,
∵,,,
∴,
∴.
(2)解:如图所示,过点作,
∴,
∵,
∴,
∴,
∴,
即,
∵在中,,,
∴,
∴,
∵,,
∴.
20 . 在综合与实践课上,同学们以“一个含的直角三角尺和两条平行线”为背景开展数学活动如图1,已知两直线,且和直角三角形,,.
(1)在图1中,,求的度数;
(2)如图2,创新小组的同学把直线向上平移,并把的位置改变,发现,说明理由;
(3)竞赛小组在创新小组发现结论的基础上,将图2中的图形继续变化得到图3,
当平分时,此时发现与又存在新的数量关系,
请写出与的数量关系并证明.
【答案】(1)
(2)理由见解析
(3),理由见解析
【分析】本题主要考查了平行的线的性质、直角三角形的性质,熟练掌握平行线的性质是解此题的关键.
(1)由可得,从而得出,最后再由两直线平行,同位角相等即可得出的度数;
(2)过点作,则,,由平行线的性质可得,结合可得,即可得解;
(3)过点作,则,,由角平分线的定义可得,从而得到,由平行线的性质可得,,计算出,即可得证.
【详解】(1)解:如图,
,
,,
,
,
,
,
;
(2)解:如图,过点作,则,
,
,
,
,
,
,
;
(3)解:,
理由如下:
如图,过点作,则,
,
平分,
,
,
,
,
,,
,
,
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
浙教版七年级数学下册第1章《平行线》单元达标检测试卷 (含解析)
选择题(本大题共有10个小题,每小题4分,共40分)
1.如图,与构成同位角的是( )
A. B. C. D.
2 . 如图,,要使,则的度数是( )
A. B. C. D.
3.如图,将直尺与含角的三角尺叠放在一起.若,则的大小是( )
A. B. C. D.
4 . 如图,下列条件中,不能判断的是( )
A. B. C. D.
5 . 如图是6级台阶侧面的示意图,如果要在台阶上铺地毯,台阶宽为2米,
那么至少要买地毯( )平方米.
A.8 B.15 C.16 D.30
6 . 如下图,下列条件中:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5,
能判定ABCD的条件为( )
A.①②③④ B.①②④ C.①③④ D.①②③
7.如图AB//CD,若∠B=120°,∠C=25°则∠1=( )
A.75° B.80° C.85° D.95°
8 .如图,AB∥CD,直线EF交AB于点E,交CD于点F,EG平分∠BEF,交CD于点G,
若∠1=50°,则∠2等于( )
A.50° B.60° C.65° D.90°
9 .如图,将△ABE向右平移2cm得到△DCF,如果△ABE的周长是16cm,
那么四边形ABFD的周长是( )
A.16cm B.18cm C.20cm D.21cm
如图,把一张对边互相平行的纸条,沿折叠,则以下结论:
①; ②; ③;
④, ⑤.
其中正确的结论有( )
A.①⑤ B.②③④ C.①②③⑤ D.①②③④⑤
填空题(本大题共有5个小题,每小题4分,共20分)
11.如图,直线a,b被c,d所截,且c⊥a,c⊥b,∠1=70°,则∠2= °.
12.如图,已知∠1=∠2,∠B=40°,则∠3= .
13 . 如图,有一块长为米,宽为3米的长方形地,中间阴影部分是一条小路,空白部分为草地,
小路的左边线向右平移1米能得到它的右边线,若草地的面积为12,则 .
如图所示,C岛在A岛的北偏东50°方向,C岛在B岛的北偏西40°方向,
则从C岛看A、B两岛的视角∠ACB等于 .
15.如图,把长方形ABCD沿EF对折,若∠1=50°,则∠AEF的度数等于 .
解答题(本大题共有5个小题,共40分)
16 . 已知:如图,直线a,b,c被直线l所截,,.求证:.
17 . 如图:在正方形网格中有一个,按要求进行下列作图(只能借助于网格):
(1)作出中边上的高;
(2)画出先将向右平移格,再向上平移格后的;
18 . 如图,E点为上的点,B为上的点,,求证:
(1)
(2)
19 . 如图,已知三角形的顶点,分别在直线和上,且.若,.
(1)当时,求的度数.
(2)设,,求和的数量关系(用含,的等式表示).
20 . 在综合与实践课上,同学们以“一个含的直角三角尺和两条平行线”为背景开展数学活动,
如图1,已知两直线,且和直角三角形,,.
(1)在图1中,,求的度数;
(2)如图2,创新小组的同学把直线向上平移,并把的位置改变,发现,说明理由;
(3)竞赛小组在创新小组发现结论的基础上,将图2中的图形继续变化得到图3,
当平分时,此时发现与又存在新的数量关系,
请写出与的数量关系并证明.
浙教版七年级数学下册第1章《平行线》单元达标检测试卷 解析
一、选择题(本大题共有10个小题,每小题4分,共40分)
1.如图,与构成同位角的是( )
A. B. C. D.
【答案】C
【分析】本题主要考查了同位角,同位角的边构成“F“形,内错角的边构成“Z“形,同旁内角的边构成“U”形.两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角.
【详解】解:直线a,b被直线m所截,与构成同位角的是,
故选:C.
2 . 如图,,要使,则的度数是( )
A. B. C. D.
【答案】D
3.如图,将直尺与含角的三角尺叠放在一起.若,则的大小是( )
A. B. C. D.
【答案】B
【分析】本题考查了平行线的性质及直角三角形的性质,充分运用三角板和直尺的几何特征是解题的关键.由三角尺可知,由平角可求,再根据平行线的性质可知.
【详解】解:如图:
由三角尺可知,
∵,
∴,
由平行线的性质可知.
故选:B.
4 . 如图,下列条件中,不能判断的是( )
A. B. C. D.
【答案】D
【分析】本题考查了平行线的判定,结合图形分析两角的位置关系,根据平行线的判定方法逐项判断即可,解题的关键是熟练掌握两直线平行的判定方法.
【详解】、由,根据内错角相等,两直线平行,可以判断,不符合题意;
、由,根据同位角相等,两直线平行,可以判断,不符合题意;
、由,根据同旁内角互补,两直线平行,可以判断,不符合题意;
、由,不可以判断,符合题意;
故选:.
5 . 如图是6级台阶侧面的示意图,如果要在台阶上铺地毯,台阶宽为2米,
那么至少要买地毯( )平方米.
A.8 B.15 C.16 D.30
【答案】C
【分析】本题考查有关平移的性质、面积计算,将图形中较短的竖线左移,较短的横线上移,平移线段后,地毯的长度是长5米,宽3米的长方形的一组邻边长度和.地毯的面积=楼梯宽度×矩形的长.
【详解】解:(平方米),
(平方米),
∴至少要买地毯16平方米.
故选:C.
6 . 如下图,下列条件中:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5,
能判定ABCD的条件为( )
A.①②③④ B.①②④ C.①③④ D.①②③
【答案】C
【详解】解:①∵∠B+∠BCD=180°
∴ABCD
②∵∠1=∠2
∴ADBC
③∵∠3=∠4
∴ABCD
④∵∠B=∠5
∴ABCD
∴能得到ABCD的条件是①③④.
故选C.
7.如图AB//CD,若∠B=120°,∠C=25°则∠1=( )
A.75° B.80° C.85° D.95°
【答案】C
【分析】首先过点作,由,可得,利用平行线的性质,即可求得与的度数,继而求得答案.
【详解】解:过点作,
,
,,
,
故选:C.
8 .如图,AB∥CD,直线EF交AB于点E,交CD于点F,EG平分∠BEF,交CD于点G,
若∠1=50°,则∠2等于( )
A.50° B.60° C.65° D.90°
【答案】C
【详解】∵AB∥CD,
∴∠BEF+∠1=180°(两直线平行,同旁内角互补)
∵∠1=50°,
∴∠BEF=130°
∵EG平分∠BEF,
∴∠BEG=∠BEF=65°(角平分线的定义)
∴∠2=∠BEG=65°(两直线平行,内错角相等),
故选C
9 .如图,将△ABE向右平移2cm得到△DCF,如果△ABE的周长是16cm,
那么四边形ABFD的周长是( )
A.16cm B.18cm C.20cm D.21cm
【答案】C
【详解】试题分析:已知,△ABE向右平移2cm得到△DCF,
根据平移的性质得到EF=AD=2cm,AE=DF,
又因△ABE的周长为16cm,
所以AB+BC+AC=16cm,
则四边形ABFD的周长=AB+BC+CF+DF+AD=16cm+2cm+2cm=20cm.
故答案选C.
10.如图,把一张对边互相平行的纸条,沿折叠,则以下结论:①;②;③; ④, ⑤.其中正确的结论有( )
A.①⑤ B.②③④ C.①②③⑤ D.①②③④⑤
【答案】D
【分析】根据平行线的性质,以及折叠的性质即可判断①,根据平行线的性质可得,,即可判断②,根据平行线的性质可得,根据对等角相等可得,即可判断③,根据平行线的性质得出,根据邻补角的定义,即可判断④,根据折叠的性质即可判断⑤
【详解】解:∵
∴
∵折叠,
∴,
∴,故①正确;
∵
∴
又
∴
∴,故②正确
∵
∴
又
∴,故③正确
∵,,
又
∴
∴
∵
∴,故④正确;
根据折叠的性质可得,故⑤正确,
故选:D.
二、填空题(本大题共有5个小题,每小题4分,共20分)
11.如图,直线a,b被c,d所截,且c⊥a,c⊥b,∠1=70°,则∠2= °.
【答案】70
【详解】∵c⊥a,c⊥b,
∴a∥b,
∴∠1=∠3,
∵∠2=∠3,
∴∠2=∠1=70°.
故答案为:70
12.如图,已知∠1=∠2,∠B=40°,则∠3= .
【答案】40°/40度
【详解】∵∠1=∠2,
∴AB//CE,
∴∠3=∠B=40°.
故答案为40°.
13 . 如图,有一块长为米,宽为3米的长方形地,中间阴影部分是一条小路,空白部分为草地,
小路的左边线向右平移1米能得到它的右边线,若草地的面积为12,则 .
【答案】5
【分析】根据小路的左边线向右平移1米能得到它的右边线,可得路的宽度是1米,根据平移,可把路移到左边,再根据面积公式,可得答案.
【详解】解:依题意有3a-3×1=12,
解得a=5.
故答案为:5.
14 . 如图所示,C岛在A岛的北偏东50°方向,C岛在B岛的北偏西40°方向,
则从C岛看A、B两岛的视角∠ACB等于 .
【答案】90°
【分析】根据方位角的概念和平行线的性质即可得答案.
【详解】过点C作CD∥AE,
∵AE∥BF,
∴CD∥AE∥BF,
∴∠ACD=∠EAC=50°,∠BCD=∠CBF=40°,
∴∠ACB=∠ACD十∠BCD=50°+40°=90°.
故答案为90.
15.如图,把长方形ABCD沿EF对折,若∠1=50°,则∠AEF的度数等于 .
【答案】
【详解】解:∵把长方形ABCD沿EF对折,
∴AD∥BC,∠BFE=∠2,
∵∠1=50°,∠1+∠2+∠BFE=180°,
∴∠BFE==65°,
∵∠AEF+∠BFE=180°,
∴∠AEF=115°.
故答案为:115°.
三 . 解答题(本大题共有5个小题,共40分)
16 . 已知:如图,直线a,b,c被直线l所截,,.求证:.
证明:∵,
∴______(______).
∵,
∴______(______).
∴(______).
【答案】见解析
【分析】根据平行线的判定即可正确求解.
【详解】证明:∵,
∴b(同旁内角互补,两直线平行).
∵,
∴ c(同位角相等,两直线平行).
∴(如果两条直线都与第三条直线平行,那么这两条直线也互相平行).
17 . 如图:在正方形网格中有一个,按要求进行下列作图(只能借助于网格):
(1)作出中边上的高;
(2)画出先将向右平移格,再向上平移格后的;
【答案】(1)见解析
(2)见解析
【分析】(1)要作出边上的高,即过点作直线的垂线,网格中的横线与竖线互相垂直;
(2)首先找出的三个顶点按要求平移后的位置,然后顺次连接各点,即可得到.
【详解】(1)解:如图所示;即为所求;
(2)如图所示,即为所求.
完成下面的证明.
18 . 如图,E点为上的点,B为上的点,,求证:
(1)
(2)
【答案】(1)证明见解析
(2)证明见解析
【分析】(1)先由对顶角相等,得到:,然后根据等量代换得到:,然后根据同位角相等两直线平行,得到;
(2)根据两直线平行,同位角相等,得到,然后根据等量代换得到:,最后根据内错角相等两直线平行,即可得到.
【详解】(1)∵,,
∴,
∴;
(2)∵
∴,
∵,
∴,
∴.
19 . 如图,已知三角形的顶点,分别在直线和上,且.若,.
(1)当时,求的度数.
(2)设,,求和的数量关系(用含,的等式表示).
【答案】(1)
(2)
【分析】(1)根据两直线平行,同旁内角互补即可求解;
(2)过点过点作,可得,根据两直线平行,同旁内角互补得到,,由此得到,在中,,由此即可求解.
【详解】(1)解:∵,
∴,即,
∵,,,
∴,
∴.
(2)解:如图所示,过点作,
∴,
∵,
∴,
∴,
∴,
即,
∵在中,,,
∴,
∴,
∵,,
∴.
20 . 在综合与实践课上,同学们以“一个含的直角三角尺和两条平行线”为背景开展数学活动如图1,已知两直线,且和直角三角形,,.
(1)在图1中,,求的度数;
(2)如图2,创新小组的同学把直线向上平移,并把的位置改变,发现,说明理由;
(3)竞赛小组在创新小组发现结论的基础上,将图2中的图形继续变化得到图3,
当平分时,此时发现与又存在新的数量关系,
请写出与的数量关系并证明.
【答案】(1)
(2)理由见解析
(3),理由见解析
【分析】本题主要考查了平行的线的性质、直角三角形的性质,熟练掌握平行线的性质是解此题的关键.
(1)由可得,从而得出,最后再由两直线平行,同位角相等即可得出的度数;
(2)过点作,则,,由平行线的性质可得,结合可得,即可得解;
(3)过点作,则,,由角平分线的定义可得,从而得到,由平行线的性质可得,,计算出,即可得证.
【详解】(1)解:如图,
,
,,
,
,
,
,
;
(2)解:如图,过点作,则,
,
,
,
,
,
,
;
(3)解:,
理由如下:
如图,过点作,则,
,
平分,
,
,
,
,
,,
,
,
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
