2024学年浙江七年级数学下学期第一章《平行线》易错题精选(含解析)
文档属性
| 名称 | 2024学年浙江七年级数学下学期第一章《平行线》易错题精选(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 469.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
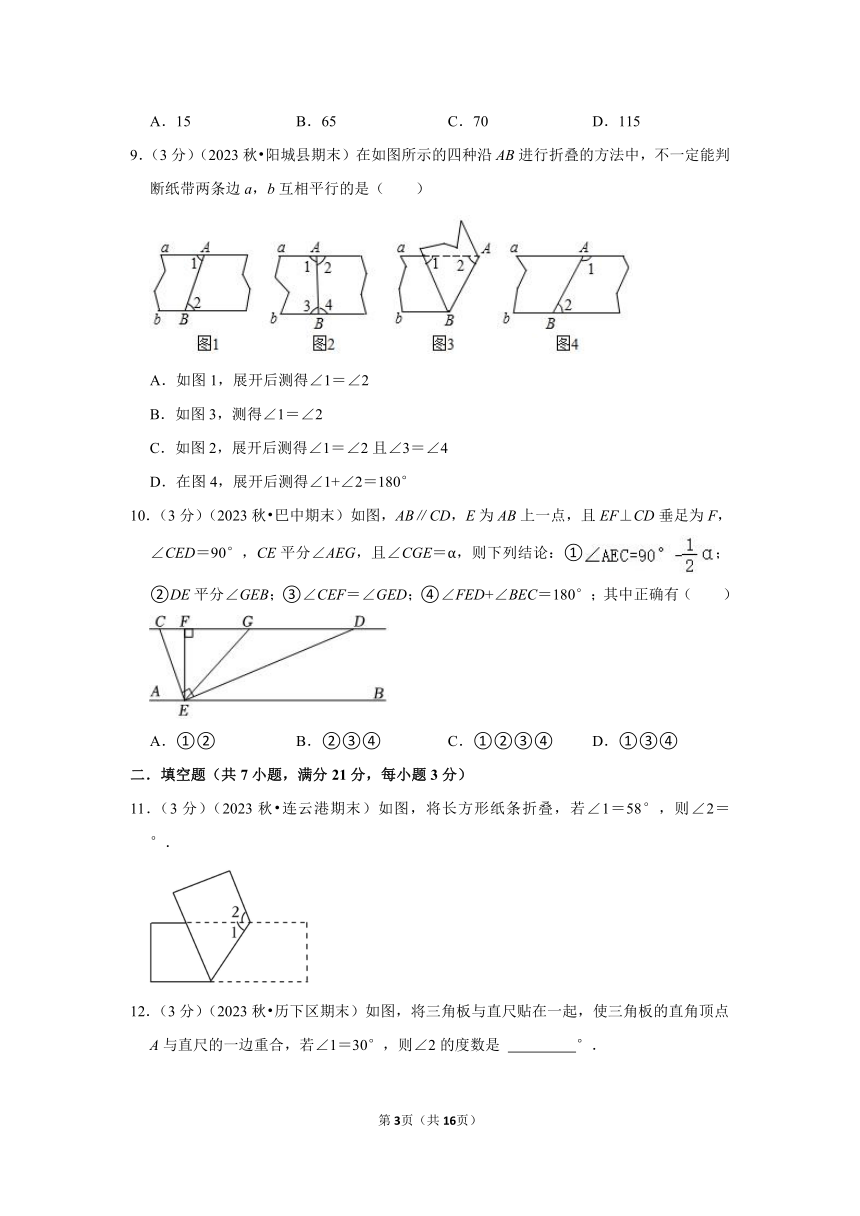
| 科目 | 数学 | ||
| 更新时间 | 2024-02-19 16:51:15 | ||
图片预览



文档简介
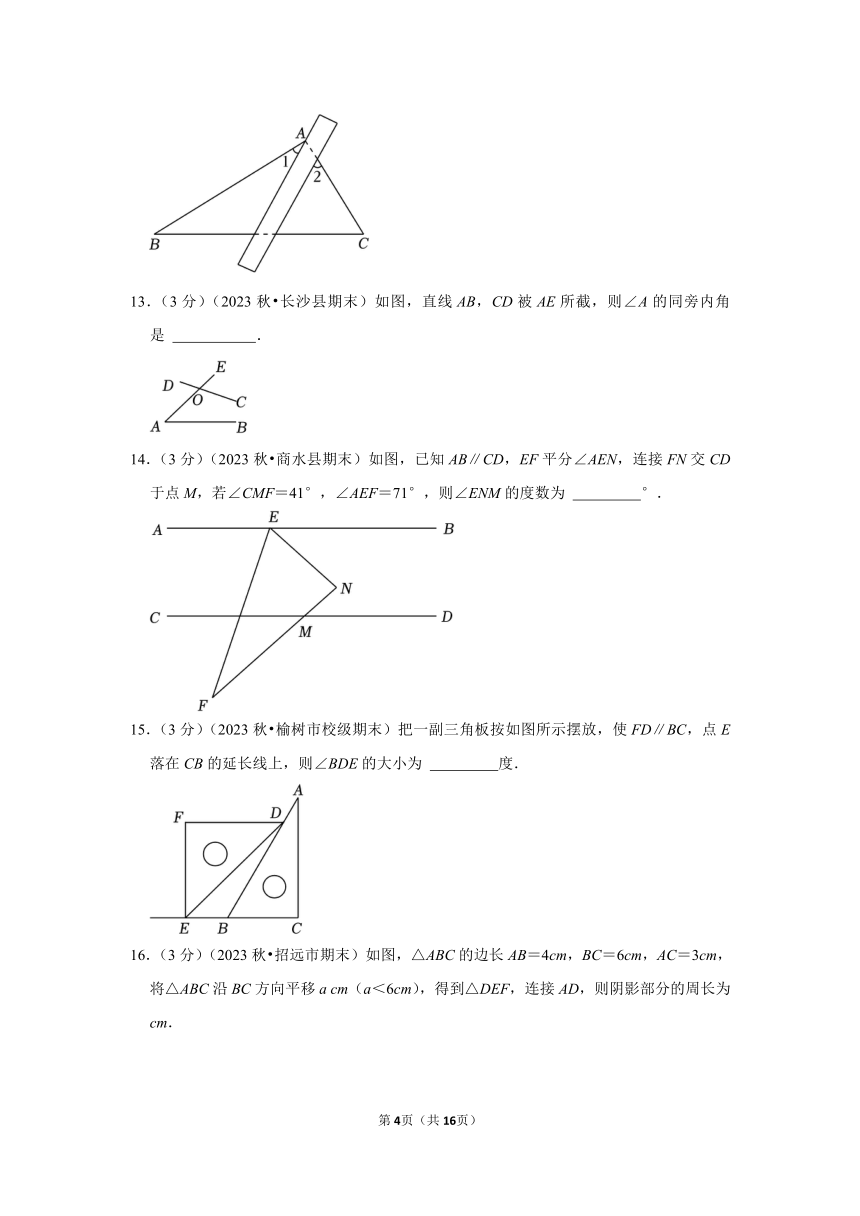
2023-2024学年浙江七年级数学下学期第一章《平行线》易错题精选
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)(2023秋 衡山县期末)下列所示的四个图形中,∠1和∠2是同位角的是( )
A.②③ B.①②③ C.③④ D.①②④
2.(3分)(2023 南充)如图,将△ABC沿BC向右平移得到△DEF,若BC=5,BE=2,则CF的长是( )
A.2 B.2.5 C.3 D.5
3.(3分)(2023秋 雁峰区期末)如图,不能判断l1∥l2的条件是( )
A.∠1=∠3 B.∠4=∠5
C.∠2=∠3 D.∠2+∠4=180°
4.(3分)(2023秋 宜州区期末)把一块直尺与一块三角板如图放置,若∠1=42°,则∠2的度数为( )
A.125° B.120° C.130° D.132°
5.(3分)(2023秋 太康县期末)如图,BC⊥AE,垂足为C,CD∥AB,∠A=50°,则∠BCD的度数是( )
A.40° B.50° C.60° D.70°
6.(3分)(2023秋 盐城期末)课堂上探究“对顶角相等”时,进行了如下推理,其推理的依据为( )
因为∠1+∠2=180°,∠2+∠3=180°所以∠1=∠3(依据:)
A.平角的定义 B.同角的余角相等
C.同角的补角相等 D.同位角相等
7.(3分)(2023秋 榆树市校级期末)平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.如图①.一束光线m射到平面镜a上,被a反射后的光线为n,则∠1=∠2.如图②,一束光AB先后经平面镜OM、ON反射后,反射光线CD与AB平行.若∠ABM=25°,则∠DCN的大小为( )
A.85° B.75° C.65° D.25°
8.(3分)(2023秋 莲池区期末)我市为了方便市民绿色出行,推出了共享单车服务.图①是某品牌共享单车放在水平地面的实物图,图②是其示意图,其中AB,CD都与地面l平行,∠BCD=60°,∠BAC=50°,当∠MAC为( )度时,AM∥BE.
A.15 B.65 C.70 D.115
9.(3分)(2023秋 阳城县期末)在如图所示的四种沿AB进行折叠的方法中,不一定能判断纸带两条边a,b互相平行的是( )
A.如图1,展开后测得∠1=∠2
B.如图3,测得∠1=∠2
C.如图2,展开后测得∠1=∠2且∠3=∠4
D.在图4,展开后测得∠1+∠2=180°
10.(3分)(2023秋 巴中期末)如图,AB∥CD,E为AB上一点,且EF⊥CD垂足为F,∠CED=90°,CE平分∠AEG,且∠CGE=α,则下列结论:①;②DE平分∠GEB;③∠CEF=∠GED;④∠FED+∠BEC=180°;其中正确有( )
A.①② B.②③④ C.①②③④ D.①③④
二.填空题(共7小题,满分21分,每小题3分)
11.(3分)(2023秋 连云港期末)如图,将长方形纸条折叠,若∠1=58°,则∠2= °.
12.(3分)(2023秋 历下区期末)如图,将三角板与直尺贴在一起,使三角板的直角顶点A与直尺的一边重合,若∠1=30°,则∠2的度数是 °.
13.(3分)(2023秋 长沙县期末)如图,直线AB,CD被AE所截,则∠A的同旁内角是 .
14.(3分)(2023秋 商水县期末)如图,已知AB∥CD,EF平分∠AEN,连接FN交CD于点M,若∠CMF=41°,∠AEF=71°,则∠ENM的度数为 °.
15.(3分)(2023秋 榆树市校级期末)把一副三角板按如图所示摆放,使FD∥BC,点E落在CB的延长线上,则∠BDE的大小为 度.
16.(3分)(2023秋 招远市期末)如图,△ABC的边长AB=4cm,BC=6cm,AC=3cm,将△ABC沿BC方向平移a cm(a<6cm),得到△DEF,连接AD,则阴影部分的周长为 cm.
17.(3分)(2023春 泉州期末)如图,将长方形纸片ABCD沿EF折叠(折线EF交AD于E,交BC于F,点C,D的落点分别是C′、D′,ED′交BC于G,再将四边形C′D′GF沿FG折叠,点C′、D′的落点分别是C″、D″,GD″交EF于H,下列四个结论:①∠GEF=∠GFE;②EF∥C″D″;③∠AEG﹣∠FEG=∠EFC″;④∠EHG=3∠EFB.其中正确的结论是 (填写序号).
三.解答题(共6小题,满分49分)
18.(6分)(2023秋 惠安县期末)如图,EF∥AD,∠1=∠2,∠BAC=82°,根据求∠AGD的解答过程填空(理由或数学式).
解:∵EF∥AD,(已知)
∴∠2=∠ ( ).
又∵∠1=∠2
∴∠1=∠3( ),
∴AB∥ ( ),
∴∠BAC+∠ =180°( ).
∵∠BAC=82°(已知),
∴∠AGD= (等式的性质)
19.(8分)(2023秋 龙岗区校级期末)如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)请说明:AB∥CD;
(2)若∠EHF=80°,∠D=30°,求∠AEM的度数.
20.(8分)(2022秋 林甸县期末)如图,点E在AC上,点F在CB的延长线上,AB与EF交于点G,∠AGE=∠CED,ED平分∠CEF.
(1)求证:AB∥DE;
(2)若∠F=30°,∠AGE=50°,求∠C的度数.
21.(8分)(2023秋 商水县期末)如图,已知DE∥CB,∠B=∠D.
(1)判断AB、CD是否平行,并说明理由.
(2)若∠B+∠F=102°,求∠DEF的度数.
22.(9分)(2023秋 郓城县期末)如图,∠1+∠2=180°,∠A=∠3.
(1)求证:AB∥CD;
(2)若∠B=78°,∠BDE=2∠3,求∠DEA的度数.
23.(10分)(2023秋 泉州期末)如图1,直线AB∥CD,三角形PMN是含30°角的直角三角板,∠MPN=90°.
(1)求∠BMP+∠DNP的度数.
(2)若NP平分∠DNM,试说明MN平分∠AMP,并写出推理过程.
(3)如图2,ME平分∠AMP,FN平分∠PND,直线ME与直线FN相交于点E,试判断∠MPN与∠MEN之间的数量关系,并说明理由.
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.【解答】解:图①②④中,∠1和∠2是同位角,
故选:D.
2.【解答】解:由平移的性质可知:CF=BE=2,
故选:A.
3.【解答】解:A、∵∠1=∠3,
∴l1∥l2,故此选项不合题意;
B、∵∠4=∠5,
∴l1∥l2,故此选项不合题意;
C、∠2=∠3,无法得出l1∥l2,故此选项符合题意;
D、∵∠2+∠4=180°,
∴l1∥l2,故此选项不合题意;
故选:C.
4.【解答】解:
∵EF∥GH,
∴∠FCD=∠2,
∵∠FCD=∠1+∠A,∠1=42°,∠A=90°,
∴∠2=∠FCD=132°,
故选:D.
5.【解答】解:∵BC⊥AE,
∴∠ACB=90°,
∵∠A=50°,
∴∠B=180°﹣∠ACB﹣∠A=40°,
∵CD∥AB,
∴∠BCD=∠B=40°.
故选:A.
6.【解答】解:∵∠1+∠2=180°,∠2+∠3=180°(平角的定义),
所以∠1=∠3(同角的补角相等).
故选:C.
7.【解答】解:由题意得∠ABM=∠CBO,∠BCO=∠DCN,
∵∠ABM=25°,
∴∠CBO=25°,
∴∠ABC=180°﹣∠ABM﹣∠CBO=180°﹣25°﹣25°=130°,
∵AB∥CD,
∴∠ABC+∠BCD=180°,
∴∠BCD=50°,
∵∠BCD+∠BCO+∠DCN=180°,
∴∠DCN=65°,
故选:C.
8.【解答】解:∵AB∥l,CD∥l,
∴AB∥CD,
∴∠BCD=∠ABC=60°,
∵∠BAC=50°,
∴∠ACB=180°﹣∠BAC﹣∠ABC=70°,
∴当∠MAC=∠ACB=70°时,AM∥BE,
故选:C.
9.【解答】解:A、当∠1=∠2时,a∥b,故此选项不符合题意;
B、∠1=∠2不能判定a,b互相平行,故此选项符合题意;
C、由∠1=∠2且∠3=∠4可得∠1=∠2=∠3=∠4=90°,∴a∥b,故此选项不符合题意;
D、由∠1+∠2=180°可知a∥b,故此选项不符合题意;
故选:B.
10.【解答】解:∵∠CGE=a,AB∥CD,
∴∠CGE=∠GEB=a,
∴∠AEG=180°﹣a,
∵CE平分∠AEG,
∴∠AEC=∠CEG=∠AEG=90°﹣a,
故①正确;
∵∠CED=90°,
∴∠AEC+∠DEB=90°,
∴∠DEB=a=∠GEB,
即DE平分∠GEB,
故②正确;
∵EF⊥CD,AB∥CD,
∴∠AEF=90°,
∴∠AEC+∠CEF=90°,
∴∠CEF=a,
∵∠GED=∠GEB﹣∠DEB=a,
∴∠CEF=∠GED,
故③正确;
∵∠FED=90°﹣∠BED=90°﹣a,
∠BEC=180°﹣∠AEC=90°+a,
∴∠FED+∠BEC=180°,
故④正确;
综上所述,正确的有①②③④,
故选:C.
二.填空题(共7小题,满分21分,每小题3分)
11.【解答】解:根据平行线的性质、折叠的性质可得:
∠1+∠2=180°﹣∠1,
∵∠1=58°,
∴58°+∠2=180°﹣58°,
∠2=64°.
故答案为:64.
12.【解答】解:∵∠1+∠3=90°,∠1=30°,
∴∠3=90°﹣∠1=60°,
∵直尺的两边平行,
∴∠2=∠3=60°
故答案为:60.
13.【解答】解:∵直线AB,CD被AE所截,
∴∠A的同旁内角是∠AOC.
故答案为:∠AOC.
14.【解答】解:过点N作NG∥AB,
∵EF平分∠AEN,∠AEF=71°,
∴∠AEN=2∠AEF=142°,
∴∠BEN=180°﹣∠AEN=180°﹣142°=38°,
∵NG∥AB,
∴∠ENG=∠BEN=38°,
∵AB∥CD,NG∥AB,∠CMF=41°,
∴GN∥CD,
∴∠GNM=∠CMF=41°,
∴∠ENM=∠ENG+∠GNM=38°+41°=79°.
故答案为:79.
15.【解答】解:由题意得:∠EDF=45°,∠ABC=60°,
∵FD∥BC,
∴∠BDF=∠ABC=60°,
∴∠BDE=∠BDF﹣∠EDF=15°.
故答案为:15.
16.【解答】解:∵将△ABC沿BC方向平移a cm(a<6cm),得到△DEF,
∴AD=BE,AB=DE,AC=DF,
∴阴影部分的周长=AD+EC+DE+AC=BE+EC+AC+AB=AB+AC+BC=4+3+6=13cm,
故答案为:13.
17.【解答】解:①∵AD∥BC,
∴∠DEF=∠GFE.
又∵∠GEF=∠DEF,
∴∠GEF=∠GFE.
故①正确.
②∵∠GEF=∠GFE,但∠FGD″不一定与∠EGD″相等,
∴EF不一定垂直于GD″,
∴EF不一定与C″D″平行.
故②不正确.
③∵AD∥BC,
∴∠AEG+∠GEF=∠EFC″+∠CFC″.
∵FC′∥GD′,
∴∠CFC″=∠CFC′=∠D′GF=∠BGE=∠GEF+∠FED=∠GEF+∠GFE.
∴∠AEG+∠GEF=∠EFC″+∠CFC″=∠EFC″+∠GEF+∠GFE,
∴∠AEG﹣∠FEG=∠EFC″.
故③正确.
④∠EHG=∠EFB+∠D″GF.
∵∠D″GF=∠D′GF=∠EGB=∠GED=∠GEF+∠FED=2∠EFB,
∴∠EHG=∠EFB+∠D″GF=∠EFB+2∠EFB=3∠EFB.
故④正确.
三.解答题(共6小题,满分49分)
18.【解答】解:∵EF∥AD,(已知)
∴∠2=∠3(两直线平行,同位角相等).
又∵∠1=∠2
∴∠1=∠3(等量代换),
∴AB∥DG(内错角相等,两直线平行),
∴∠BAC+∠AGD=180°(两直线平行,同旁内角互补).
∵∠BAC=82°(已知),
∴∠AGD=98°(等式的性质)
故答案为:3;两直线平行,同位角相等;等量代换;DG;内错角相等,两直线平行;AGD;两直线平行,同旁内角互补;98°.
19.【解答】(1)证明:∵∠CED=∠GHD,
∴CE∥GF,
∴∠C=∠FGD,
又∵∠C=∠EFG,
∴∠FGD=∠EFG,
∴AB∥CD;
(2)解:∵∠GHD=∠EHF=80°,∠D=30°,
∴∠CGF=∠GHD+∠D=80°+30°=110°,
又∵CE∥GF,
∴∠C+∠CGF=180°,
∴∠C=180°﹣110°=70°,
又∵AB∥CD,
∴∠AEC=∠C=70°,
∴∠AEM=180°﹣70°=110°.
20.【解答】(1)证明:∵ED平分∠CEF,
∴∠DEF=∠CED,
∵∠AGE=∠CED,
∴∠AGE=∠DEF,
∴AB∥DE;
(2)解:∵∠AGE=∠CED,∠AGE=50°,
∴∠CED=50°,
∵ED平分∠CEF,
∴∠CEF=2∠CED=100°,
∵∠C+∠CEF+∠F=180°,∠F=30°,
∴∠C=180°﹣100°﹣30°=50°.
21.【解答】解:(1)AB∥CD,理由如下:
∵DE∥CB,
∴∠D=∠BCF,
∵∠B=∠D,
∴∠BCF=∠B,
∴AB∥CD;
(2)∵DE∥CB,
∴∠B+∠BED=180°,
∴∠B+∠BEF+∠DEF=180°,
∵AB∥CD,
∴∠F=∠BEF,
∴∠B+∠F+∠DEF=180°,
∵∠B+∠F=102°,
∴∠DEF=78°.
22.【解答】解:(1)∵∠1+∠2=180°,
∴DE∥AC,
∴∠A=∠DEB,
∵∠A=∠3,
∴∠3=∠DEB,
∴AB∥CD;
(2)∵AB∥CD,
∴∠BDC+∠B=180°,
∵∠B=78°,∠BDE=2∠3,
∴2∠3+∠3+78°=180°,
∴∠3=34°,
∵AB∥CD,
∴∠3+∠DEA=180°,
∴∠DEA=146°.
23.【解答】解:(1)过点P作PE∥AB,
∴∠BMP=∠1,
∵AB∥CD,
∴PE∥CD,
∴∠DNP=∠2,
∵∠MPN=90°,
∴∠BMP+∠DNP=∠1+∠2=∠MPN=90°.
(2)∵NP平分∠DNM,∠MNP=30°,
∴∠MND=2∠MNP=60°,
∵AB∥CD,
∴∠AMN=∠MND=60°,
∵∠NMP=60°,
∴∠AMN=∠NMP,
∴MN平分∠AMP.
(3)∠MEN=MPN,理由如下:
∵ME平分∠AMP,
∴∠EMP=∠AMP=(180°﹣∠BMP)=∠BMP,
∵∠NMP=60°,
∴∠EMN=∠EMP﹣∠NMP=90°﹣∠BMP﹣60°=30°﹣∠BMP,
∵FN平分∠PND,
∴∠PNF=∠PND,
∵∠MNP=30°,
∴∠MNF=∠MNP+∠PNF=30°+∠PND,
∵∠MNF=∠MEN+∠EMN,
∴∠MEN=∠MNF﹣∠EMN=30°+∠PND﹣(30°﹣∠BMP)=(∠PND+∠BMP),
由(1)可知∠BMP+∠PND=∠MPN,
∴∠MEN=MPN.
第1页(共1页)
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)(2023秋 衡山县期末)下列所示的四个图形中,∠1和∠2是同位角的是( )
A.②③ B.①②③ C.③④ D.①②④
2.(3分)(2023 南充)如图,将△ABC沿BC向右平移得到△DEF,若BC=5,BE=2,则CF的长是( )
A.2 B.2.5 C.3 D.5
3.(3分)(2023秋 雁峰区期末)如图,不能判断l1∥l2的条件是( )
A.∠1=∠3 B.∠4=∠5
C.∠2=∠3 D.∠2+∠4=180°
4.(3分)(2023秋 宜州区期末)把一块直尺与一块三角板如图放置,若∠1=42°,则∠2的度数为( )
A.125° B.120° C.130° D.132°
5.(3分)(2023秋 太康县期末)如图,BC⊥AE,垂足为C,CD∥AB,∠A=50°,则∠BCD的度数是( )
A.40° B.50° C.60° D.70°
6.(3分)(2023秋 盐城期末)课堂上探究“对顶角相等”时,进行了如下推理,其推理的依据为( )
因为∠1+∠2=180°,∠2+∠3=180°所以∠1=∠3(依据:)
A.平角的定义 B.同角的余角相等
C.同角的补角相等 D.同位角相等
7.(3分)(2023秋 榆树市校级期末)平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.如图①.一束光线m射到平面镜a上,被a反射后的光线为n,则∠1=∠2.如图②,一束光AB先后经平面镜OM、ON反射后,反射光线CD与AB平行.若∠ABM=25°,则∠DCN的大小为( )
A.85° B.75° C.65° D.25°
8.(3分)(2023秋 莲池区期末)我市为了方便市民绿色出行,推出了共享单车服务.图①是某品牌共享单车放在水平地面的实物图,图②是其示意图,其中AB,CD都与地面l平行,∠BCD=60°,∠BAC=50°,当∠MAC为( )度时,AM∥BE.
A.15 B.65 C.70 D.115
9.(3分)(2023秋 阳城县期末)在如图所示的四种沿AB进行折叠的方法中,不一定能判断纸带两条边a,b互相平行的是( )
A.如图1,展开后测得∠1=∠2
B.如图3,测得∠1=∠2
C.如图2,展开后测得∠1=∠2且∠3=∠4
D.在图4,展开后测得∠1+∠2=180°
10.(3分)(2023秋 巴中期末)如图,AB∥CD,E为AB上一点,且EF⊥CD垂足为F,∠CED=90°,CE平分∠AEG,且∠CGE=α,则下列结论:①;②DE平分∠GEB;③∠CEF=∠GED;④∠FED+∠BEC=180°;其中正确有( )
A.①② B.②③④ C.①②③④ D.①③④
二.填空题(共7小题,满分21分,每小题3分)
11.(3分)(2023秋 连云港期末)如图,将长方形纸条折叠,若∠1=58°,则∠2= °.
12.(3分)(2023秋 历下区期末)如图,将三角板与直尺贴在一起,使三角板的直角顶点A与直尺的一边重合,若∠1=30°,则∠2的度数是 °.
13.(3分)(2023秋 长沙县期末)如图,直线AB,CD被AE所截,则∠A的同旁内角是 .
14.(3分)(2023秋 商水县期末)如图,已知AB∥CD,EF平分∠AEN,连接FN交CD于点M,若∠CMF=41°,∠AEF=71°,则∠ENM的度数为 °.
15.(3分)(2023秋 榆树市校级期末)把一副三角板按如图所示摆放,使FD∥BC,点E落在CB的延长线上,则∠BDE的大小为 度.
16.(3分)(2023秋 招远市期末)如图,△ABC的边长AB=4cm,BC=6cm,AC=3cm,将△ABC沿BC方向平移a cm(a<6cm),得到△DEF,连接AD,则阴影部分的周长为 cm.
17.(3分)(2023春 泉州期末)如图,将长方形纸片ABCD沿EF折叠(折线EF交AD于E,交BC于F,点C,D的落点分别是C′、D′,ED′交BC于G,再将四边形C′D′GF沿FG折叠,点C′、D′的落点分别是C″、D″,GD″交EF于H,下列四个结论:①∠GEF=∠GFE;②EF∥C″D″;③∠AEG﹣∠FEG=∠EFC″;④∠EHG=3∠EFB.其中正确的结论是 (填写序号).
三.解答题(共6小题,满分49分)
18.(6分)(2023秋 惠安县期末)如图,EF∥AD,∠1=∠2,∠BAC=82°,根据求∠AGD的解答过程填空(理由或数学式).
解:∵EF∥AD,(已知)
∴∠2=∠ ( ).
又∵∠1=∠2
∴∠1=∠3( ),
∴AB∥ ( ),
∴∠BAC+∠ =180°( ).
∵∠BAC=82°(已知),
∴∠AGD= (等式的性质)
19.(8分)(2023秋 龙岗区校级期末)如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)请说明:AB∥CD;
(2)若∠EHF=80°,∠D=30°,求∠AEM的度数.
20.(8分)(2022秋 林甸县期末)如图,点E在AC上,点F在CB的延长线上,AB与EF交于点G,∠AGE=∠CED,ED平分∠CEF.
(1)求证:AB∥DE;
(2)若∠F=30°,∠AGE=50°,求∠C的度数.
21.(8分)(2023秋 商水县期末)如图,已知DE∥CB,∠B=∠D.
(1)判断AB、CD是否平行,并说明理由.
(2)若∠B+∠F=102°,求∠DEF的度数.
22.(9分)(2023秋 郓城县期末)如图,∠1+∠2=180°,∠A=∠3.
(1)求证:AB∥CD;
(2)若∠B=78°,∠BDE=2∠3,求∠DEA的度数.
23.(10分)(2023秋 泉州期末)如图1,直线AB∥CD,三角形PMN是含30°角的直角三角板,∠MPN=90°.
(1)求∠BMP+∠DNP的度数.
(2)若NP平分∠DNM,试说明MN平分∠AMP,并写出推理过程.
(3)如图2,ME平分∠AMP,FN平分∠PND,直线ME与直线FN相交于点E,试判断∠MPN与∠MEN之间的数量关系,并说明理由.
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.【解答】解:图①②④中,∠1和∠2是同位角,
故选:D.
2.【解答】解:由平移的性质可知:CF=BE=2,
故选:A.
3.【解答】解:A、∵∠1=∠3,
∴l1∥l2,故此选项不合题意;
B、∵∠4=∠5,
∴l1∥l2,故此选项不合题意;
C、∠2=∠3,无法得出l1∥l2,故此选项符合题意;
D、∵∠2+∠4=180°,
∴l1∥l2,故此选项不合题意;
故选:C.
4.【解答】解:
∵EF∥GH,
∴∠FCD=∠2,
∵∠FCD=∠1+∠A,∠1=42°,∠A=90°,
∴∠2=∠FCD=132°,
故选:D.
5.【解答】解:∵BC⊥AE,
∴∠ACB=90°,
∵∠A=50°,
∴∠B=180°﹣∠ACB﹣∠A=40°,
∵CD∥AB,
∴∠BCD=∠B=40°.
故选:A.
6.【解答】解:∵∠1+∠2=180°,∠2+∠3=180°(平角的定义),
所以∠1=∠3(同角的补角相等).
故选:C.
7.【解答】解:由题意得∠ABM=∠CBO,∠BCO=∠DCN,
∵∠ABM=25°,
∴∠CBO=25°,
∴∠ABC=180°﹣∠ABM﹣∠CBO=180°﹣25°﹣25°=130°,
∵AB∥CD,
∴∠ABC+∠BCD=180°,
∴∠BCD=50°,
∵∠BCD+∠BCO+∠DCN=180°,
∴∠DCN=65°,
故选:C.
8.【解答】解:∵AB∥l,CD∥l,
∴AB∥CD,
∴∠BCD=∠ABC=60°,
∵∠BAC=50°,
∴∠ACB=180°﹣∠BAC﹣∠ABC=70°,
∴当∠MAC=∠ACB=70°时,AM∥BE,
故选:C.
9.【解答】解:A、当∠1=∠2时,a∥b,故此选项不符合题意;
B、∠1=∠2不能判定a,b互相平行,故此选项符合题意;
C、由∠1=∠2且∠3=∠4可得∠1=∠2=∠3=∠4=90°,∴a∥b,故此选项不符合题意;
D、由∠1+∠2=180°可知a∥b,故此选项不符合题意;
故选:B.
10.【解答】解:∵∠CGE=a,AB∥CD,
∴∠CGE=∠GEB=a,
∴∠AEG=180°﹣a,
∵CE平分∠AEG,
∴∠AEC=∠CEG=∠AEG=90°﹣a,
故①正确;
∵∠CED=90°,
∴∠AEC+∠DEB=90°,
∴∠DEB=a=∠GEB,
即DE平分∠GEB,
故②正确;
∵EF⊥CD,AB∥CD,
∴∠AEF=90°,
∴∠AEC+∠CEF=90°,
∴∠CEF=a,
∵∠GED=∠GEB﹣∠DEB=a,
∴∠CEF=∠GED,
故③正确;
∵∠FED=90°﹣∠BED=90°﹣a,
∠BEC=180°﹣∠AEC=90°+a,
∴∠FED+∠BEC=180°,
故④正确;
综上所述,正确的有①②③④,
故选:C.
二.填空题(共7小题,满分21分,每小题3分)
11.【解答】解:根据平行线的性质、折叠的性质可得:
∠1+∠2=180°﹣∠1,
∵∠1=58°,
∴58°+∠2=180°﹣58°,
∠2=64°.
故答案为:64.
12.【解答】解:∵∠1+∠3=90°,∠1=30°,
∴∠3=90°﹣∠1=60°,
∵直尺的两边平行,
∴∠2=∠3=60°
故答案为:60.
13.【解答】解:∵直线AB,CD被AE所截,
∴∠A的同旁内角是∠AOC.
故答案为:∠AOC.
14.【解答】解:过点N作NG∥AB,
∵EF平分∠AEN,∠AEF=71°,
∴∠AEN=2∠AEF=142°,
∴∠BEN=180°﹣∠AEN=180°﹣142°=38°,
∵NG∥AB,
∴∠ENG=∠BEN=38°,
∵AB∥CD,NG∥AB,∠CMF=41°,
∴GN∥CD,
∴∠GNM=∠CMF=41°,
∴∠ENM=∠ENG+∠GNM=38°+41°=79°.
故答案为:79.
15.【解答】解:由题意得:∠EDF=45°,∠ABC=60°,
∵FD∥BC,
∴∠BDF=∠ABC=60°,
∴∠BDE=∠BDF﹣∠EDF=15°.
故答案为:15.
16.【解答】解:∵将△ABC沿BC方向平移a cm(a<6cm),得到△DEF,
∴AD=BE,AB=DE,AC=DF,
∴阴影部分的周长=AD+EC+DE+AC=BE+EC+AC+AB=AB+AC+BC=4+3+6=13cm,
故答案为:13.
17.【解答】解:①∵AD∥BC,
∴∠DEF=∠GFE.
又∵∠GEF=∠DEF,
∴∠GEF=∠GFE.
故①正确.
②∵∠GEF=∠GFE,但∠FGD″不一定与∠EGD″相等,
∴EF不一定垂直于GD″,
∴EF不一定与C″D″平行.
故②不正确.
③∵AD∥BC,
∴∠AEG+∠GEF=∠EFC″+∠CFC″.
∵FC′∥GD′,
∴∠CFC″=∠CFC′=∠D′GF=∠BGE=∠GEF+∠FED=∠GEF+∠GFE.
∴∠AEG+∠GEF=∠EFC″+∠CFC″=∠EFC″+∠GEF+∠GFE,
∴∠AEG﹣∠FEG=∠EFC″.
故③正确.
④∠EHG=∠EFB+∠D″GF.
∵∠D″GF=∠D′GF=∠EGB=∠GED=∠GEF+∠FED=2∠EFB,
∴∠EHG=∠EFB+∠D″GF=∠EFB+2∠EFB=3∠EFB.
故④正确.
三.解答题(共6小题,满分49分)
18.【解答】解:∵EF∥AD,(已知)
∴∠2=∠3(两直线平行,同位角相等).
又∵∠1=∠2
∴∠1=∠3(等量代换),
∴AB∥DG(内错角相等,两直线平行),
∴∠BAC+∠AGD=180°(两直线平行,同旁内角互补).
∵∠BAC=82°(已知),
∴∠AGD=98°(等式的性质)
故答案为:3;两直线平行,同位角相等;等量代换;DG;内错角相等,两直线平行;AGD;两直线平行,同旁内角互补;98°.
19.【解答】(1)证明:∵∠CED=∠GHD,
∴CE∥GF,
∴∠C=∠FGD,
又∵∠C=∠EFG,
∴∠FGD=∠EFG,
∴AB∥CD;
(2)解:∵∠GHD=∠EHF=80°,∠D=30°,
∴∠CGF=∠GHD+∠D=80°+30°=110°,
又∵CE∥GF,
∴∠C+∠CGF=180°,
∴∠C=180°﹣110°=70°,
又∵AB∥CD,
∴∠AEC=∠C=70°,
∴∠AEM=180°﹣70°=110°.
20.【解答】(1)证明:∵ED平分∠CEF,
∴∠DEF=∠CED,
∵∠AGE=∠CED,
∴∠AGE=∠DEF,
∴AB∥DE;
(2)解:∵∠AGE=∠CED,∠AGE=50°,
∴∠CED=50°,
∵ED平分∠CEF,
∴∠CEF=2∠CED=100°,
∵∠C+∠CEF+∠F=180°,∠F=30°,
∴∠C=180°﹣100°﹣30°=50°.
21.【解答】解:(1)AB∥CD,理由如下:
∵DE∥CB,
∴∠D=∠BCF,
∵∠B=∠D,
∴∠BCF=∠B,
∴AB∥CD;
(2)∵DE∥CB,
∴∠B+∠BED=180°,
∴∠B+∠BEF+∠DEF=180°,
∵AB∥CD,
∴∠F=∠BEF,
∴∠B+∠F+∠DEF=180°,
∵∠B+∠F=102°,
∴∠DEF=78°.
22.【解答】解:(1)∵∠1+∠2=180°,
∴DE∥AC,
∴∠A=∠DEB,
∵∠A=∠3,
∴∠3=∠DEB,
∴AB∥CD;
(2)∵AB∥CD,
∴∠BDC+∠B=180°,
∵∠B=78°,∠BDE=2∠3,
∴2∠3+∠3+78°=180°,
∴∠3=34°,
∵AB∥CD,
∴∠3+∠DEA=180°,
∴∠DEA=146°.
23.【解答】解:(1)过点P作PE∥AB,
∴∠BMP=∠1,
∵AB∥CD,
∴PE∥CD,
∴∠DNP=∠2,
∵∠MPN=90°,
∴∠BMP+∠DNP=∠1+∠2=∠MPN=90°.
(2)∵NP平分∠DNM,∠MNP=30°,
∴∠MND=2∠MNP=60°,
∵AB∥CD,
∴∠AMN=∠MND=60°,
∵∠NMP=60°,
∴∠AMN=∠NMP,
∴MN平分∠AMP.
(3)∠MEN=MPN,理由如下:
∵ME平分∠AMP,
∴∠EMP=∠AMP=(180°﹣∠BMP)=∠BMP,
∵∠NMP=60°,
∴∠EMN=∠EMP﹣∠NMP=90°﹣∠BMP﹣60°=30°﹣∠BMP,
∵FN平分∠PND,
∴∠PNF=∠PND,
∵∠MNP=30°,
∴∠MNF=∠MNP+∠PNF=30°+∠PND,
∵∠MNF=∠MEN+∠EMN,
∴∠MEN=∠MNF﹣∠EMN=30°+∠PND﹣(30°﹣∠BMP)=(∠PND+∠BMP),
由(1)可知∠BMP+∠PND=∠MPN,
∴∠MEN=MPN.
第1页(共1页)
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
