浙教版七年级数学下册第1章《平行线》单元检测试卷(含解析)
文档属性
| 名称 | 浙教版七年级数学下册第1章《平行线》单元检测试卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-20 17:37:48 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
浙教版七年级数学下册第1章《平行线》单元检测试卷(含解析)
选择题(本大题共有10个小题,每小题4分,共40分)
如图所示的车标,可以看作由平移得到的是( )
A. B. C. D.
2.如图,AB∥CD,若∠2=135°,那么∠1的度数是( )
A.30° B.45° C.60° D.75°
3.如图,已知直线,被直线所截,的同旁内角是( )
A. B. C. D.
4.如图所示,已知,,则的度数是( )
A. B. C. D.
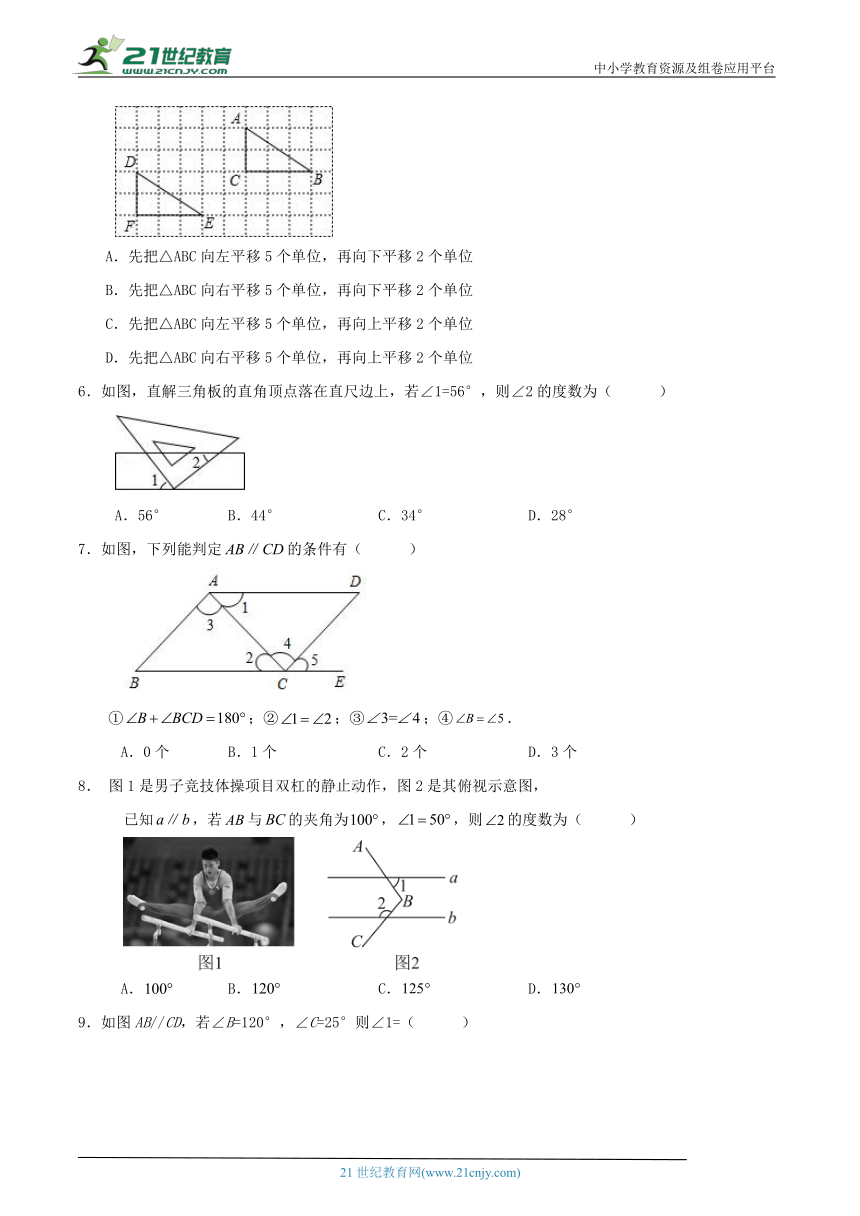
如图,在10×6的网格中,每个小方格的边长都是1个单位,将△ABC平移到△DEF的位置,
下面正确的平移步骤是( )
A.先把△ABC向左平移5个单位,再向下平移2个单位
B.先把△ABC向右平移5个单位,再向下平移2个单位
C.先把△ABC向左平移5个单位,再向上平移2个单位
D.先把△ABC向右平移5个单位,再向上平移2个单位
6.如图,直解三角板的直角顶点落在直尺边上,若∠1=56°,则∠2的度数为( )
A.56° B.44° C.34° D.28°
7.如图,下列能判定的条件有( )
①;②;③;④.
A.0个 B.1个 C.2个 D.3个
图1是男子竞技体操项目双杠的静止动作,图2是其俯视示意图,
已知,若与的夹角为,,则的度数为( )
A. B. C. D.
9.如图AB//CD,若∠B=120°,∠C=25°则∠1=( )
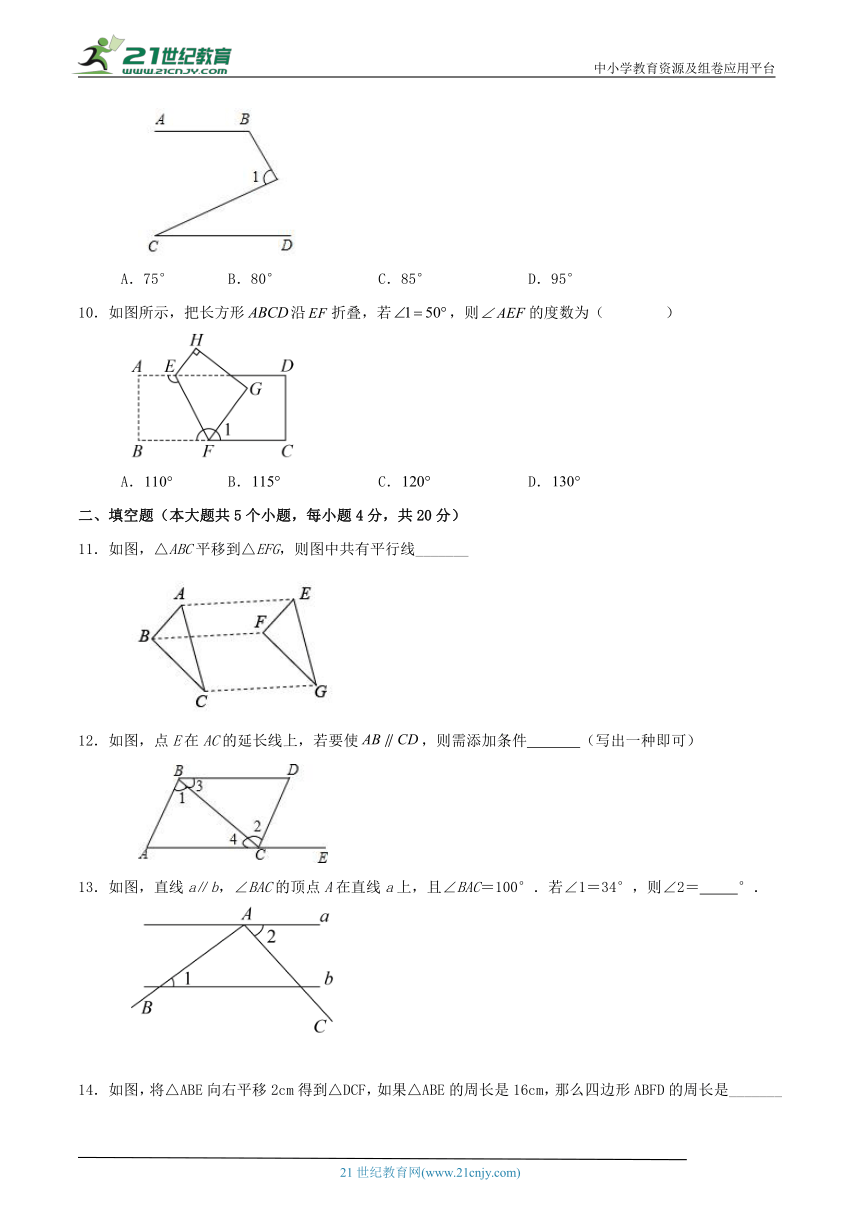
A.75° B.80° C.85° D.95°
10.如图所示,把长方形沿折叠,若,则的度数为( )
A. B. C. D.
填空题(本大题共5个小题,每小题4分,共20分)
11.如图,△ABC平移到△EFG,则图中共有平行线_______
12.如图,点E在AC的延长线上,若要使,则需添加条件 (写出一种即可)
13.如图,直线a∥b,∠BAC的顶点A在直线a上,且∠BAC=100°.若∠1=34°,则∠2= °.
如图,将△ABE向右平移2cm得到△DCF,如果△ABE的周长是16cm,那么四边形ABFD的周长是_______
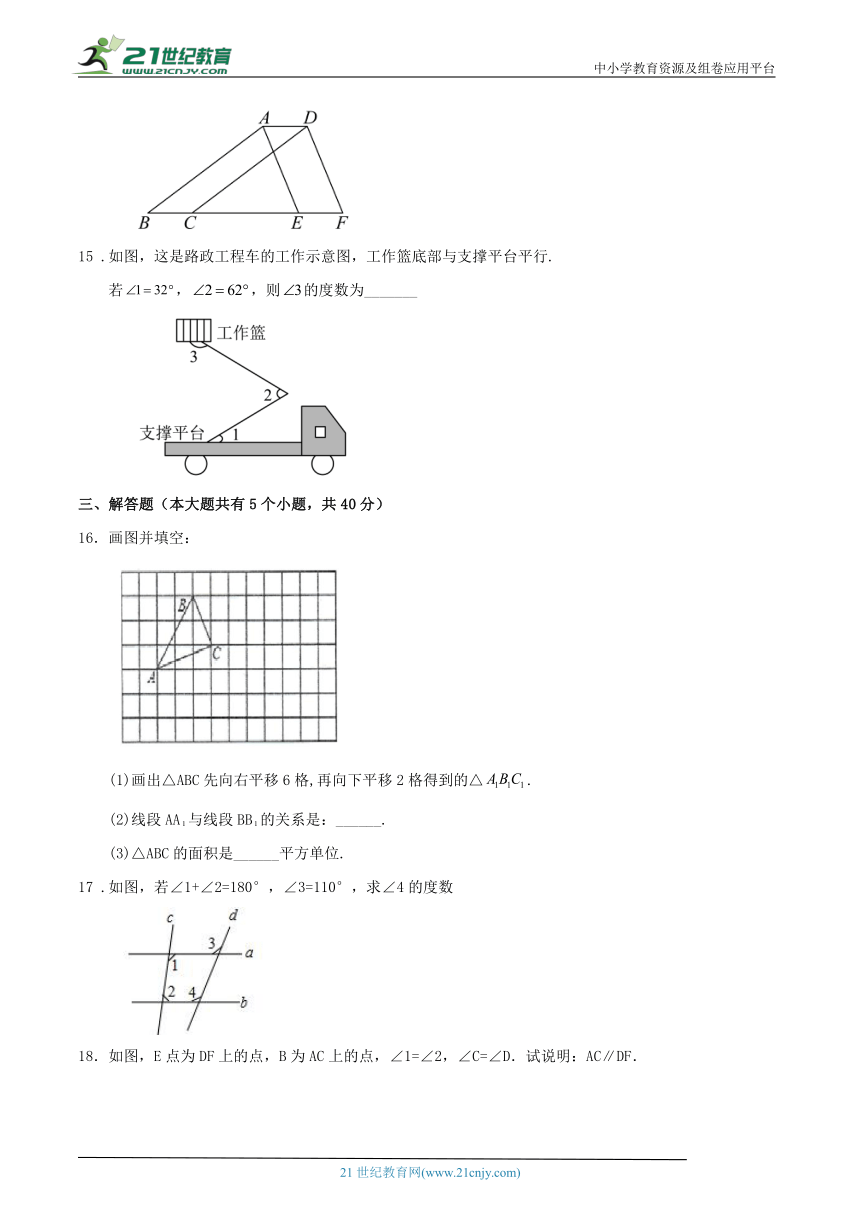
15 .如图,这是路政工程车的工作示意图,工作篮底部与支撑平台平行.
若,,则的度数为_______
三、解答题(本大题共有5个小题,共40分)
16.画图并填空:
(1)画出△ABC先向右平移6格,再向下平移2格得到的△.
(2)线段AA与线段BB的关系是:______.
(3)△ABC的面积是______平方单位.
17 .如图,若∠1+∠2=180°,∠3=110°,求∠4的度数
18.如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D.试说明:AC∥DF.
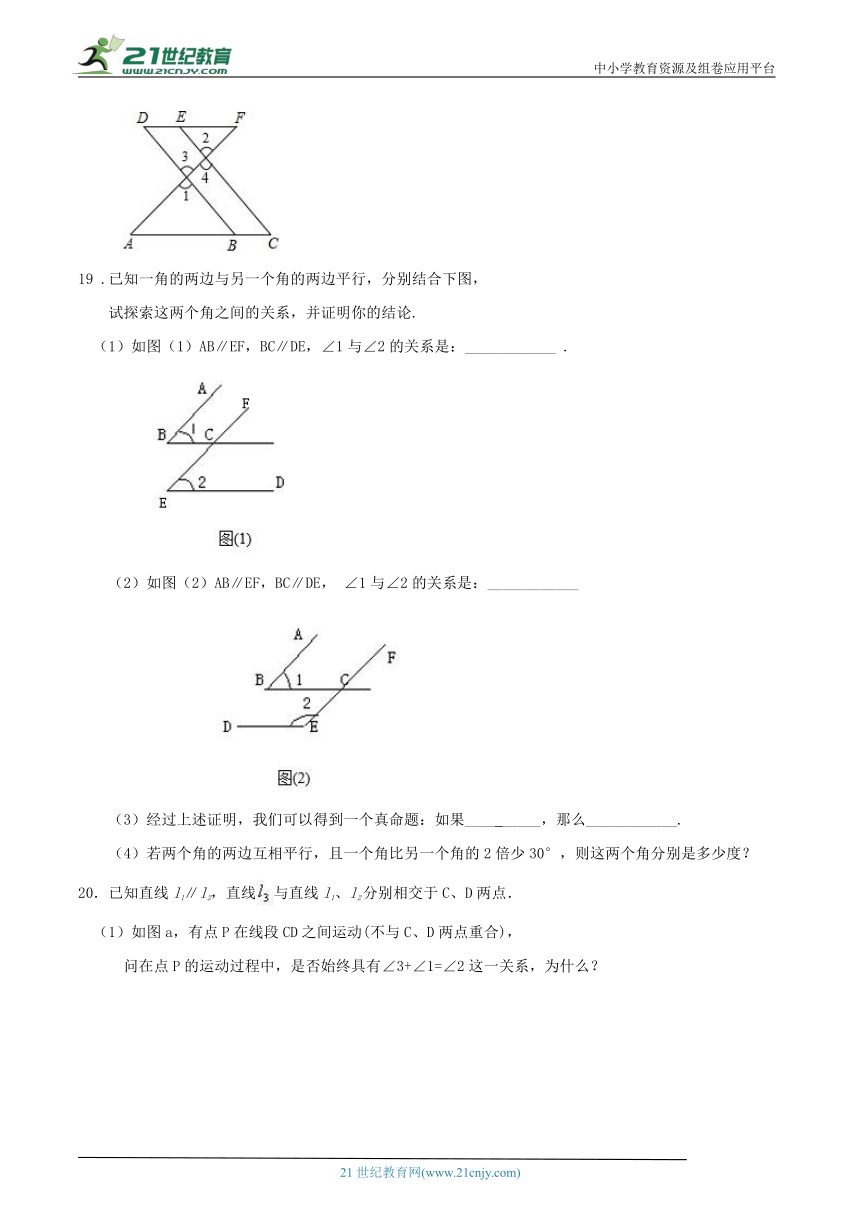
19 .已知一角的两边与另一个角的两边平行,分别结合下图,
试探索这两个角之间的关系,并证明你的结论.
(1)如图(1)AB∥EF,BC∥DE,∠1与∠2的关系是:____________ .
(2)如图(2)AB∥EF,BC∥DE, ∠1与∠2的关系是:____________
(3)经过上述证明,我们可以得到一个真命题:如果____ _____,那么____________.
(4)若两个角的两边互相平行,且一个角比另一个角的2倍少30°,则这两个角分别是多少度?
20.已知直线l1∥l2,直线与直线l1、l2分别相交于C、D两点.
(1)如图a,有点P在线段CD之间运动(不与C、D两点重合),
问在点P的运动过程中,是否始终具有∠3+∠1=∠2这一关系,为什么?
如图b,当点P在线段CD之外运动(不与C、D两点重合),问上述结论是否成立
若不成立,试写出新的结论并说明理由.
浙教版七年级数学下册第1章《平行线》单元检测试卷 解析
一、选择题(本大题共有10个小题,每小题4分,共40分)
1 .如图所示的车标,可以看作由平移得到的是( )
A. B. C. D.
【答案】B
【分析】根据平移的概念:在平面内,把一个图形整体沿某一方向移动,这种图形的平行移动,叫做平移变换,简称平移,即可选出答案.
【详解】解:根据平移的概念可知四个车标中只有B选项中的车标是经过平移得到的,
故选B.
2.如图,AB∥CD,若∠2=135°,那么∠1的度数是( )
A.30° B.45° C.60° D.75°
【答案】B
【详解】试题分析:由AB∥CD,知∠1的对顶角与∠2互补,
所以∠1=45°.
故选:B
3.如图,已知直线,被直线所截,的同旁内角是( )
A. B. C. D.
【答案】A
【分析】两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角.
【详解】∵直线,被直线所截,
∴的同旁内角是.
故选:A.
4.如图所示,已知,,则的度数是( )
A. B. C. D.
【答案】A
【分析】根据“对顶角相等”和“两直线平行,同旁内角互补”求解即可.
【详解】解:如下图,
∵,
∴,
∵,
∴.
故选:A.
5 . 如图,在10×6的网格中,每个小方格的边长都是1个单位,将△ABC平移到△DEF的位置,
下面正确的平移步骤是( )
A.先把△ABC向左平移5个单位,再向下平移2个单位
B.先把△ABC向右平移5个单位,再向下平移2个单位
C.先把△ABC向左平移5个单位,再向上平移2个单位
D.先把△ABC向右平移5个单位,再向上平移2个单位
【答案】A
【详解】解:根据网格结构,观察点对应点A、D,点A向左平移5个单位,再向下平移2个单位即可到达点D的位置,
所以,平移步骤是:先把△ABC向左平移5个单位,再向下平移2个单位.
故选A.
6.如图,直解三角板的直角顶点落在直尺边上,若∠1=56°,则∠2的度数为( )
A.56° B.44° C.34° D.28°
【答案】C
【分析】由平角的定义得到∠3=34°;然后根据“两直线平行,内错角相等”求出∠2的度数.
【详解】如图,
依题意知∠1+∠3=90°.
∵∠1=56°,
∴∠3=34°.
∵直尺的两边互相平行,
∴∠2=∠3=34°,
故选C.
7.如图,下列能判定的条件有( )
①;②;③;④.
A.0个 B.1个 C.2个 D.3个
【答案】D
【分析】根据题目中的条件,可以写出各个小题中的条件可以得到哪两条线平行,从而可以解答本题.
【详解】解:①∵∠B+∠BCD=180°,
∴ABCD,故①符合题意;
②∵∠1=∠2,
∴ADBC,故②不符合题意;
③∵∠3=∠4,
∴ABCD,故③符合题意;
④∵∠B=∠5,
∴ABCD,故④符合题意;
故选:D.
8 . 图1是男子竞技体操项目双杠的静止动作,图2是其俯视示意图,
已知,若与的夹角为,,则的度数为( )
A. B. C. D.
【答案】D
【分析】过点B作,则,利用平行线的性质,进行求解即可.
【详解】解:如图,过点B作,
∵,
∴,
∴,,
∵,
∴,
∴.
故选:D.
9.如图AB//CD,若∠B=120°,∠C=25°则∠1=( )
A.75° B.80° C.85° D.95°
【答案】C
【分析】首先过点作,由,可得,利用平行线的性质,即可求得与的度数,继而求得答案.
【详解】解:过点作,
,
,,
,
故选:C.
10.如图所示,把长方形沿折叠,若,则的度数为( )
A. B. C. D.
【答案】B
【分析】先根据折叠的性质和平角的定义求出,再根据平行线的性质即可得到.
【详解】解:由折叠的性质可得,
∵,
∴,
∵,
∴,
故选B.
填空题(本大题共5个小题,每小题4分,共20分)
11.如图,△ABC平移到△EFG,则图中共有平行线_______
【答案】6对
【分析】根据经过平移,对应点所连的线段平行且相等,对应线段平行且相等作答.
【详解】解:∵△ABC平移得到△EFG,A的对应点为E,B的对应点为F,C的对应点为G,
∴ABEF,BCFG,ACEG,AECG,AEBF,BFCG,共6对.
故答案为:6对
12.如图,点E在AC的延长线上,若要使,则需添加条件 (写出一种即可)
【答案】∠1=∠2 等 (写出一种即可)
【分析】根据平行线的判定定理得出直接得出即可.
【详解】解:∵当∠1 =∠2时,(内错角相等,两直线平行);
∴若要使,则需添加条件∠1 =∠2;
故答案为:∠1=∠2.
13.如图,直线a∥b,∠BAC的顶点A在直线a上,且∠BAC=100°.若∠1=34°,则∠2= °.
【答案】46
【分析】根据平行线的性质和平角的定义即可得到结论.
【详解】解:∵直线a∥b,
∴∠3=∠1=34°,
∵∠BAC=100°,
∴∠2=180° 34° 100°=46°,
故答案为:46.
14 .如图,将△ABE向右平移2cm得到△DCF,如果△ABE的周长是16cm,那么四边形ABFD的周长是_______
【答案】 20cm
【详解】试题分析:已知,△ABE向右平移2cm得到△DCF,
根据平移的性质得到EF=AD=2cm,AE=DF,
又因△ABE的周长为16cm,
所以AB+BC+AC=16cm,
则四边形ABFD的周长=AB+BC+CF+DF+AD=16cm+2cm+2cm=20cm.
故答案选 : 20cm
15 .如图,这是路政工程车的工作示意图,工作篮底部与支撑平台平行.
若,,则的度数为_______
【答案】
【分析】过点作工作篮底部,根据平行线的性质及角的和差求解即可.
【详解】解:如图,过点作工作篮底部,
,
工作篮底部与支撑平台平行,工作篮底部
支撑平台,
,
,,
,
,
故答案为:
三、解答题(本大题共有5个小题,共40分)
16.画图并填空:
(1)画出△ABC先向右平移6格,再向下平移2格得到的△.
(2)线段AA与线段BB的关系是:______.
(3)△ABC的面积是______平方单位.
【答案】(1)见解析;(2)平行且相等;(3)3.5.
【分析】(1)根据网格结构找出点A、B、C的位置,然后顺次连接即可;
(2)根据平移的性质,对应点的连线平行且相等;
(3)利用△ABC所在的正方形的面积减去四周三个小直角三角形的面积,列式计算即可得解.
【详解】(1)△如图所示;
(2)AA与线段BB平行且相等;
(3)△ABC的面积=3×3 ×2×3 ×3×1 ×2×1=9 3 1.5 1=3.5,
故答案为平行且相等;3.5.
17 .如图,若∠1+∠2=180°,∠3=110°,求∠4的度数
【答案】110°.
【详解】解:∵∠1+∠2=180°,
∴a∥b,∴∠3=∠4,
又∵∠3=110°,∴∠4=110°.
故答案为110°.
18.如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D.试说明:AC∥DF.
【答案】证明见解析
【分析】先根据对顶角相等结合∠1=∠2推出∠3=∠2,然后根据同位角相等,两直线平行证明BD∥CE,再根据两直线平行,同位角相等得到∠ABD=∠C,从而推出∠ABD=∠D,再根据内错角相等,两直线平行证明AC∥DF,然后根据两直线平行,内错角相等即可得证.
【详解】证明:,
,
,
,
,
,
.
19 .已知一角的两边与另一个角的两边平行,分别结合下图,
试探索这两个角之间的关系,并证明你的结论.
(1)如图(1)AB∥EF,BC∥DE,∠1与∠2的关系是:____________ .
(2)如图(2)AB∥EF,BC∥DE, ∠1与∠2的关系是:____________
(3)经过上述证明,我们可以得到一个真命题:如果____ _____,那么____________.
(4)若两个角的两边互相平行,且一个角比另一个角的2倍少30°,则这两个角分别是多少度?
【答案】(1)∠1=∠2,证明见解析;(2)∠1+∠2=180°,证明见解析;(3)一个角的两边与另一个角的两边分别平行,这两个角相等或互补;(4)这两个角分别是30°,30°或70°,110°.
【分析】(1)根据两直线平行,内错角相等,可求出∠1=∠2;
(2)根据两直线平行,内错角相等及同旁内角互补可求出∠1+∠2=180°;
(3)由(1)(2)可得出结论;
(4)由(3)可列出方程,求出角的度数.
【详解】解:(1)AB∥EF,BC∥DE,∠1与∠2的关系是:∠1=∠2
证明:∵AB∥EF
∴∠1=∠BCE
∵BC∥DE
∴∠2=∠BCE
∴∠1=∠2.
(2)AB∥EF,BC∥DE.∠1与∠2的关系是:∠1+∠2=180°.
证明:∵AB∥EF
∴∠1=∠BCE
∵BC∥DE
∴∠2+∠BCE=180°
∴∠1+∠2=180°.
(3)经过上述证明,我们可以得到一个真命题:如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补.
(4)解:设其中一个角为x°,列方程得x=2x-30或x+2x-30=180,
故x=30或x=70,
所以2x-30=30或110,
答:这两个角分别是30°,30°或70°,110°.
20.已知直线l1∥l2,直线与直线l1、l2分别相交于C、D两点.
(1)如图a,有点P在线段CD之间运动(不与C、D两点重合),
问在点P的运动过程中,是否始终具有∠3+∠1=∠2这一关系,为什么?
如图b,当点P在线段CD之外运动(不与C、D两点重合),问上述结论是否成立
若不成立,试写出新的结论并说明理由.
【答案】(1)具有,证明见解析;(2)上述结论不成立, 新结论:∠1=∠2+∠3,理由见解析.
【分析】(1)相等关系成立.过点P作PE∥l1,则有∠1=∠APE,又因为PE∥l2,又有∠3=∠BPE,因为∠BPE+∠APE=∠2,所以∠3+∠1=∠2;
(2)原关系不成立,过点P作PE∥l1,则有∠1=∠APE;又因为PE∥l2,又有∠3=∠BPE,困为此时∠BPE-∠APE=∠2,则有∠3-∠1=∠2.
【详解】(1)作PE∥l1,则∠1=∠APE,
∵l1//l2,
∴l2//PE
∴∠3=∠BPE∵∠APB=∠APE+∠BPE,
∴∠APB=∠1+∠3;
(2)上述结论不成立. 新结论:∠1=∠2+∠3,
∵l1//l2,
∴∠1=∠AFB,
∵∠AFB=∠2+∠3,
∴∠1=∠2+∠3.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
浙教版七年级数学下册第1章《平行线》单元检测试卷(含解析)
选择题(本大题共有10个小题,每小题4分,共40分)
如图所示的车标,可以看作由平移得到的是( )
A. B. C. D.
2.如图,AB∥CD,若∠2=135°,那么∠1的度数是( )
A.30° B.45° C.60° D.75°
3.如图,已知直线,被直线所截,的同旁内角是( )
A. B. C. D.
4.如图所示,已知,,则的度数是( )
A. B. C. D.
如图,在10×6的网格中,每个小方格的边长都是1个单位,将△ABC平移到△DEF的位置,
下面正确的平移步骤是( )
A.先把△ABC向左平移5个单位,再向下平移2个单位
B.先把△ABC向右平移5个单位,再向下平移2个单位
C.先把△ABC向左平移5个单位,再向上平移2个单位
D.先把△ABC向右平移5个单位,再向上平移2个单位
6.如图,直解三角板的直角顶点落在直尺边上,若∠1=56°,则∠2的度数为( )
A.56° B.44° C.34° D.28°
7.如图,下列能判定的条件有( )
①;②;③;④.
A.0个 B.1个 C.2个 D.3个
图1是男子竞技体操项目双杠的静止动作,图2是其俯视示意图,
已知,若与的夹角为,,则的度数为( )
A. B. C. D.
9.如图AB//CD,若∠B=120°,∠C=25°则∠1=( )
A.75° B.80° C.85° D.95°
10.如图所示,把长方形沿折叠,若,则的度数为( )
A. B. C. D.
填空题(本大题共5个小题,每小题4分,共20分)
11.如图,△ABC平移到△EFG,则图中共有平行线_______
12.如图,点E在AC的延长线上,若要使,则需添加条件 (写出一种即可)
13.如图,直线a∥b,∠BAC的顶点A在直线a上,且∠BAC=100°.若∠1=34°,则∠2= °.
如图,将△ABE向右平移2cm得到△DCF,如果△ABE的周长是16cm,那么四边形ABFD的周长是_______
15 .如图,这是路政工程车的工作示意图,工作篮底部与支撑平台平行.
若,,则的度数为_______
三、解答题(本大题共有5个小题,共40分)
16.画图并填空:
(1)画出△ABC先向右平移6格,再向下平移2格得到的△.
(2)线段AA与线段BB的关系是:______.
(3)△ABC的面积是______平方单位.
17 .如图,若∠1+∠2=180°,∠3=110°,求∠4的度数
18.如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D.试说明:AC∥DF.
19 .已知一角的两边与另一个角的两边平行,分别结合下图,
试探索这两个角之间的关系,并证明你的结论.
(1)如图(1)AB∥EF,BC∥DE,∠1与∠2的关系是:____________ .
(2)如图(2)AB∥EF,BC∥DE, ∠1与∠2的关系是:____________
(3)经过上述证明,我们可以得到一个真命题:如果____ _____,那么____________.
(4)若两个角的两边互相平行,且一个角比另一个角的2倍少30°,则这两个角分别是多少度?
20.已知直线l1∥l2,直线与直线l1、l2分别相交于C、D两点.
(1)如图a,有点P在线段CD之间运动(不与C、D两点重合),
问在点P的运动过程中,是否始终具有∠3+∠1=∠2这一关系,为什么?
如图b,当点P在线段CD之外运动(不与C、D两点重合),问上述结论是否成立
若不成立,试写出新的结论并说明理由.
浙教版七年级数学下册第1章《平行线》单元检测试卷 解析
一、选择题(本大题共有10个小题,每小题4分,共40分)
1 .如图所示的车标,可以看作由平移得到的是( )
A. B. C. D.
【答案】B
【分析】根据平移的概念:在平面内,把一个图形整体沿某一方向移动,这种图形的平行移动,叫做平移变换,简称平移,即可选出答案.
【详解】解:根据平移的概念可知四个车标中只有B选项中的车标是经过平移得到的,
故选B.
2.如图,AB∥CD,若∠2=135°,那么∠1的度数是( )
A.30° B.45° C.60° D.75°
【答案】B
【详解】试题分析:由AB∥CD,知∠1的对顶角与∠2互补,
所以∠1=45°.
故选:B
3.如图,已知直线,被直线所截,的同旁内角是( )
A. B. C. D.
【答案】A
【分析】两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角.
【详解】∵直线,被直线所截,
∴的同旁内角是.
故选:A.
4.如图所示,已知,,则的度数是( )
A. B. C. D.
【答案】A
【分析】根据“对顶角相等”和“两直线平行,同旁内角互补”求解即可.
【详解】解:如下图,
∵,
∴,
∵,
∴.
故选:A.
5 . 如图,在10×6的网格中,每个小方格的边长都是1个单位,将△ABC平移到△DEF的位置,
下面正确的平移步骤是( )
A.先把△ABC向左平移5个单位,再向下平移2个单位
B.先把△ABC向右平移5个单位,再向下平移2个单位
C.先把△ABC向左平移5个单位,再向上平移2个单位
D.先把△ABC向右平移5个单位,再向上平移2个单位
【答案】A
【详解】解:根据网格结构,观察点对应点A、D,点A向左平移5个单位,再向下平移2个单位即可到达点D的位置,
所以,平移步骤是:先把△ABC向左平移5个单位,再向下平移2个单位.
故选A.
6.如图,直解三角板的直角顶点落在直尺边上,若∠1=56°,则∠2的度数为( )
A.56° B.44° C.34° D.28°
【答案】C
【分析】由平角的定义得到∠3=34°;然后根据“两直线平行,内错角相等”求出∠2的度数.
【详解】如图,
依题意知∠1+∠3=90°.
∵∠1=56°,
∴∠3=34°.
∵直尺的两边互相平行,
∴∠2=∠3=34°,
故选C.
7.如图,下列能判定的条件有( )
①;②;③;④.
A.0个 B.1个 C.2个 D.3个
【答案】D
【分析】根据题目中的条件,可以写出各个小题中的条件可以得到哪两条线平行,从而可以解答本题.
【详解】解:①∵∠B+∠BCD=180°,
∴ABCD,故①符合题意;
②∵∠1=∠2,
∴ADBC,故②不符合题意;
③∵∠3=∠4,
∴ABCD,故③符合题意;
④∵∠B=∠5,
∴ABCD,故④符合题意;
故选:D.
8 . 图1是男子竞技体操项目双杠的静止动作,图2是其俯视示意图,
已知,若与的夹角为,,则的度数为( )
A. B. C. D.
【答案】D
【分析】过点B作,则,利用平行线的性质,进行求解即可.
【详解】解:如图,过点B作,
∵,
∴,
∴,,
∵,
∴,
∴.
故选:D.
9.如图AB//CD,若∠B=120°,∠C=25°则∠1=( )
A.75° B.80° C.85° D.95°
【答案】C
【分析】首先过点作,由,可得,利用平行线的性质,即可求得与的度数,继而求得答案.
【详解】解:过点作,
,
,,
,
故选:C.
10.如图所示,把长方形沿折叠,若,则的度数为( )
A. B. C. D.
【答案】B
【分析】先根据折叠的性质和平角的定义求出,再根据平行线的性质即可得到.
【详解】解:由折叠的性质可得,
∵,
∴,
∵,
∴,
故选B.
填空题(本大题共5个小题,每小题4分,共20分)
11.如图,△ABC平移到△EFG,则图中共有平行线_______
【答案】6对
【分析】根据经过平移,对应点所连的线段平行且相等,对应线段平行且相等作答.
【详解】解:∵△ABC平移得到△EFG,A的对应点为E,B的对应点为F,C的对应点为G,
∴ABEF,BCFG,ACEG,AECG,AEBF,BFCG,共6对.
故答案为:6对
12.如图,点E在AC的延长线上,若要使,则需添加条件 (写出一种即可)
【答案】∠1=∠2 等 (写出一种即可)
【分析】根据平行线的判定定理得出直接得出即可.
【详解】解:∵当∠1 =∠2时,(内错角相等,两直线平行);
∴若要使,则需添加条件∠1 =∠2;
故答案为:∠1=∠2.
13.如图,直线a∥b,∠BAC的顶点A在直线a上,且∠BAC=100°.若∠1=34°,则∠2= °.
【答案】46
【分析】根据平行线的性质和平角的定义即可得到结论.
【详解】解:∵直线a∥b,
∴∠3=∠1=34°,
∵∠BAC=100°,
∴∠2=180° 34° 100°=46°,
故答案为:46.
14 .如图,将△ABE向右平移2cm得到△DCF,如果△ABE的周长是16cm,那么四边形ABFD的周长是_______
【答案】 20cm
【详解】试题分析:已知,△ABE向右平移2cm得到△DCF,
根据平移的性质得到EF=AD=2cm,AE=DF,
又因△ABE的周长为16cm,
所以AB+BC+AC=16cm,
则四边形ABFD的周长=AB+BC+CF+DF+AD=16cm+2cm+2cm=20cm.
故答案选 : 20cm
15 .如图,这是路政工程车的工作示意图,工作篮底部与支撑平台平行.
若,,则的度数为_______
【答案】
【分析】过点作工作篮底部,根据平行线的性质及角的和差求解即可.
【详解】解:如图,过点作工作篮底部,
,
工作篮底部与支撑平台平行,工作篮底部
支撑平台,
,
,,
,
,
故答案为:
三、解答题(本大题共有5个小题,共40分)
16.画图并填空:
(1)画出△ABC先向右平移6格,再向下平移2格得到的△.
(2)线段AA与线段BB的关系是:______.
(3)△ABC的面积是______平方单位.
【答案】(1)见解析;(2)平行且相等;(3)3.5.
【分析】(1)根据网格结构找出点A、B、C的位置,然后顺次连接即可;
(2)根据平移的性质,对应点的连线平行且相等;
(3)利用△ABC所在的正方形的面积减去四周三个小直角三角形的面积,列式计算即可得解.
【详解】(1)△如图所示;
(2)AA与线段BB平行且相等;
(3)△ABC的面积=3×3 ×2×3 ×3×1 ×2×1=9 3 1.5 1=3.5,
故答案为平行且相等;3.5.
17 .如图,若∠1+∠2=180°,∠3=110°,求∠4的度数
【答案】110°.
【详解】解:∵∠1+∠2=180°,
∴a∥b,∴∠3=∠4,
又∵∠3=110°,∴∠4=110°.
故答案为110°.
18.如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D.试说明:AC∥DF.
【答案】证明见解析
【分析】先根据对顶角相等结合∠1=∠2推出∠3=∠2,然后根据同位角相等,两直线平行证明BD∥CE,再根据两直线平行,同位角相等得到∠ABD=∠C,从而推出∠ABD=∠D,再根据内错角相等,两直线平行证明AC∥DF,然后根据两直线平行,内错角相等即可得证.
【详解】证明:,
,
,
,
,
,
.
19 .已知一角的两边与另一个角的两边平行,分别结合下图,
试探索这两个角之间的关系,并证明你的结论.
(1)如图(1)AB∥EF,BC∥DE,∠1与∠2的关系是:____________ .
(2)如图(2)AB∥EF,BC∥DE, ∠1与∠2的关系是:____________
(3)经过上述证明,我们可以得到一个真命题:如果____ _____,那么____________.
(4)若两个角的两边互相平行,且一个角比另一个角的2倍少30°,则这两个角分别是多少度?
【答案】(1)∠1=∠2,证明见解析;(2)∠1+∠2=180°,证明见解析;(3)一个角的两边与另一个角的两边分别平行,这两个角相等或互补;(4)这两个角分别是30°,30°或70°,110°.
【分析】(1)根据两直线平行,内错角相等,可求出∠1=∠2;
(2)根据两直线平行,内错角相等及同旁内角互补可求出∠1+∠2=180°;
(3)由(1)(2)可得出结论;
(4)由(3)可列出方程,求出角的度数.
【详解】解:(1)AB∥EF,BC∥DE,∠1与∠2的关系是:∠1=∠2
证明:∵AB∥EF
∴∠1=∠BCE
∵BC∥DE
∴∠2=∠BCE
∴∠1=∠2.
(2)AB∥EF,BC∥DE.∠1与∠2的关系是:∠1+∠2=180°.
证明:∵AB∥EF
∴∠1=∠BCE
∵BC∥DE
∴∠2+∠BCE=180°
∴∠1+∠2=180°.
(3)经过上述证明,我们可以得到一个真命题:如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补.
(4)解:设其中一个角为x°,列方程得x=2x-30或x+2x-30=180,
故x=30或x=70,
所以2x-30=30或110,
答:这两个角分别是30°,30°或70°,110°.
20.已知直线l1∥l2,直线与直线l1、l2分别相交于C、D两点.
(1)如图a,有点P在线段CD之间运动(不与C、D两点重合),
问在点P的运动过程中,是否始终具有∠3+∠1=∠2这一关系,为什么?
如图b,当点P在线段CD之外运动(不与C、D两点重合),问上述结论是否成立
若不成立,试写出新的结论并说明理由.
【答案】(1)具有,证明见解析;(2)上述结论不成立, 新结论:∠1=∠2+∠3,理由见解析.
【分析】(1)相等关系成立.过点P作PE∥l1,则有∠1=∠APE,又因为PE∥l2,又有∠3=∠BPE,因为∠BPE+∠APE=∠2,所以∠3+∠1=∠2;
(2)原关系不成立,过点P作PE∥l1,则有∠1=∠APE;又因为PE∥l2,又有∠3=∠BPE,困为此时∠BPE-∠APE=∠2,则有∠3-∠1=∠2.
【详解】(1)作PE∥l1,则∠1=∠APE,
∵l1//l2,
∴l2//PE
∴∠3=∠BPE∵∠APB=∠APE+∠BPE,
∴∠APB=∠1+∠3;
(2)上述结论不成立. 新结论:∠1=∠2+∠3,
∵l1//l2,
∴∠1=∠AFB,
∵∠AFB=∠2+∠3,
∴∠1=∠2+∠3.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
