1.3 平行线的判定 第一课时 课件 (共16张PPT)浙教版数学七年级下册
文档属性
| 名称 | 1.3 平行线的判定 第一课时 课件 (共16张PPT)浙教版数学七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 872.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 12:20:06 | ||
图片预览


文档简介
(共16张PPT)
浙教版七(下)
第一章 平行线
1.3 平行线的判定(一)
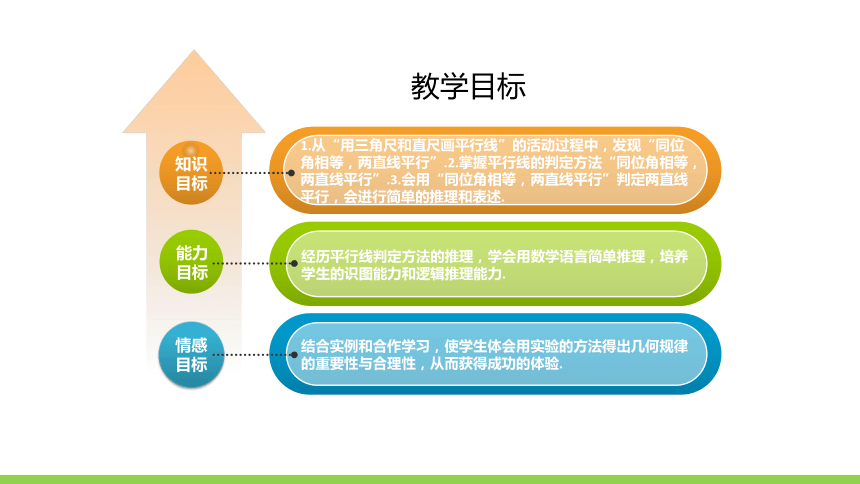
1.从“用三角尺和直尺画平行线”的活动过程中,发现“同位角相等,两直线平行”.2.掌握平行线的判定方法“同位角相等,两直线平行”.3.会用“同位角相等,两直线平行”判定两直线平行,会进行简单的推理和表述.
教学目标
经历平行线判定方法的推理,学会用数学语言简单推理,培养学生的识图能力和逻辑推理能力.
结合实例和合作学习,使学生体会用实验的方法得出几何规律的重要性与合理性,从而获得成功的体验.
知识目标
能力目标
情感目标
P
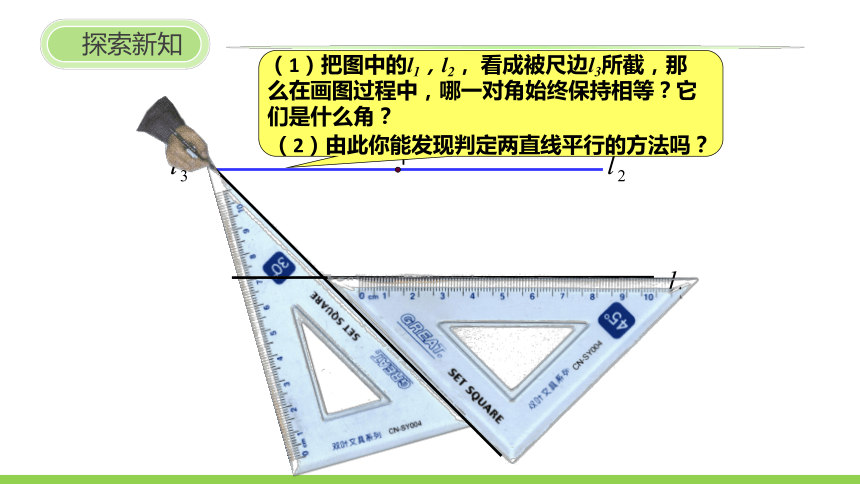
探索新知
(1)把图中的l1,l2, 看成被尺边l3所截,那么在画图过程中,哪一对角始终保持相等?它们是什么角?
(2)由此你能发现判定两直线平行的方法吗?
P
1
2
P
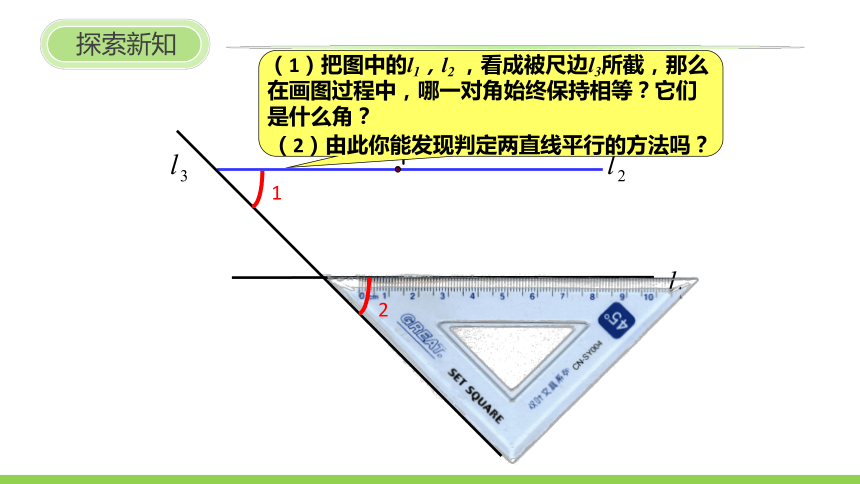
(1)把图中的l1,l2 ,看成被尺边l3所截,那么在画图过程中,哪一对角始终保持相等?它们是什么角?
(2)由此你能发现判定两直线平行的方法吗?
探索新知
(同位角相等,两直线平行)
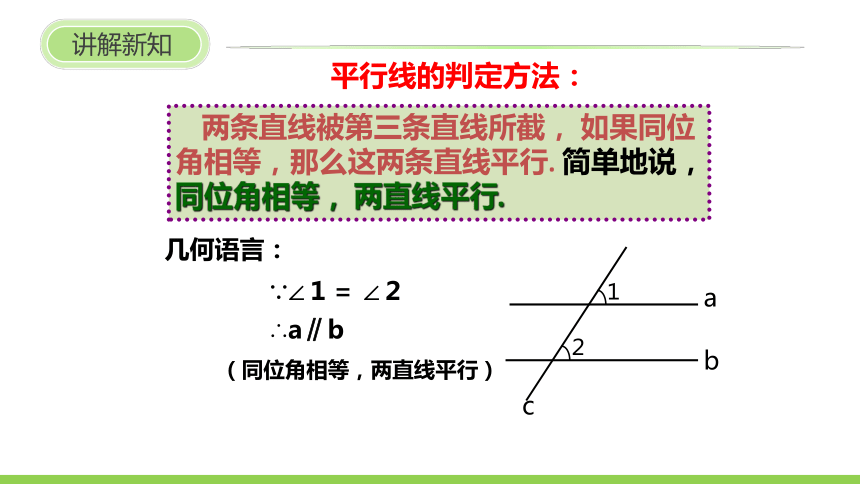
讲解新知
平行线的判定方法:
2
∵∠1= ∠2
1
a
b
c
几何语言:
∴a∥b
两条直线被第三条直线所截, 如果同位角相等,那么这两条直线平行. 简单地说,同位角相等, 两直线平行.
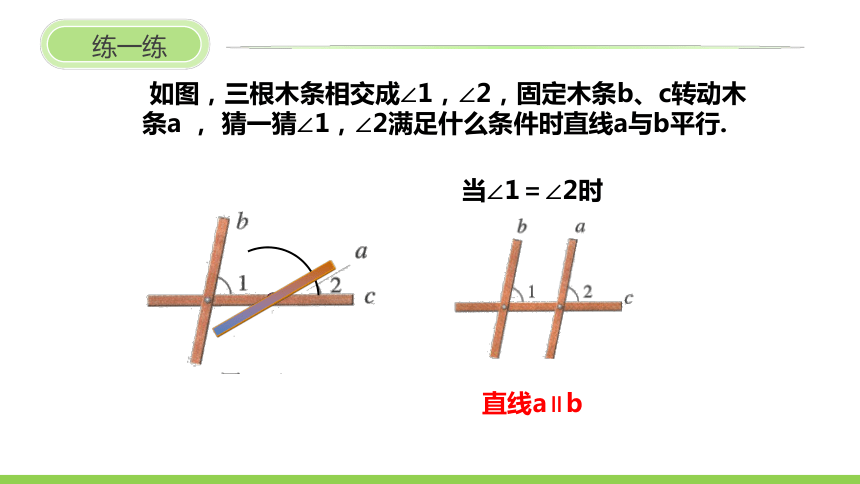
练一练
如图,三根木条相交成∠1,∠2,固定木条b、c转动木条a , 猜一猜∠1,∠2满足什么条件时直线a与b平行.
当∠1=∠2时
直线a∥b
例题分析
如图,∠2+∠3=180°,
∴ ∠3=180°-∠2
=180°-135°
=45°
又∵ ∠1=45°,
∴ ∠1=∠3.
例1 如图,直线l1,l2 被l3所截,∠1=45°,
∠2=135°,试判断l1与l2是否平行.并说明理由.
1
2
解
∥ .理由如下:
∵ ∠1与∠3是直线l1,l2 被l3所截的一对同位角,
根据“同位角相等,两直线平行”,得l1 ∥l2.
3
例题分析
例2 如图,AB⊥EF,CD⊥EF,E,F分别为垂足.直线AB与CD平行吗?请说明理由.
解
∵ AB⊥EF,CD⊥EF,
∴ ∠1=∠2=Rt∠.
∴ AB∥CD
(根据什么?)
(同位角相等,两直线平行.)
A
B
C
D
E
F
“在同一平面 ,垂直于同一条直线的两条直线互相平行”.
课内练习
1
2
1.如图,直线l1,l2 被l3所截,且∠1=∠2.直线
l1与l2平行吗?请说明理由.
课内练习
2.某人骑自行车从A出发,沿正东方向前进至B处后,右转15°,沿直线向前行驶到C处(如图).这时他想仍按正东方向行驶,那么他应怎样调整行驶方向?请画出他继续行驶的路线,并说明理由.
A
B
C
15°
拓展提高
1.如图:AB⊥CD于点B,AE与BF相交于点G,且∠FGE=60°,∠ABG=30°,请判断AE与CD是否平行,并说明理由.
A
E
F
G
C
B
D
60°
30°
拓展提高
2.如图,已知∠ABD=∠ACE,BF、CG分别是∠ABD、∠ACE的平分线,请判断BF与CG是否平行,并说明理由.
A
B
C
D
E
F
G
解:
BF∥CG
1
2
∵BF、CG分别是∠ABD、∠ACE的平分线
∴ ∠1= ∠ABD,∠2= ∠ACE
∵
∠ABD =∠ACE
∴ ∠1=∠2
∴BF∥CG
(同位角相等,两直线平行)
3.甲,乙两船只分别从A、B两个港口出发,甲沿北偏东30度方向行驶,乙沿南偏西30度方向行驶,你知道甲船的航线与乙船的航线平行吗?为什么?
E
D
A
B
C
F
1
北
南
西
东
G
拓展提高
2
小结
1.判定两直线平行的方法:
同位角相等,两直线平行.
2.用“同位角相等,两直线平行”判定两直线平行.能进行简单的推理和表述.
再见
谢谢大家!
浙教版七(下)
第一章 平行线
1.3 平行线的判定(一)
1.从“用三角尺和直尺画平行线”的活动过程中,发现“同位角相等,两直线平行”.2.掌握平行线的判定方法“同位角相等,两直线平行”.3.会用“同位角相等,两直线平行”判定两直线平行,会进行简单的推理和表述.
教学目标
经历平行线判定方法的推理,学会用数学语言简单推理,培养学生的识图能力和逻辑推理能力.
结合实例和合作学习,使学生体会用实验的方法得出几何规律的重要性与合理性,从而获得成功的体验.
知识目标
能力目标
情感目标
P
探索新知
(1)把图中的l1,l2, 看成被尺边l3所截,那么在画图过程中,哪一对角始终保持相等?它们是什么角?
(2)由此你能发现判定两直线平行的方法吗?
P
1
2
P
(1)把图中的l1,l2 ,看成被尺边l3所截,那么在画图过程中,哪一对角始终保持相等?它们是什么角?
(2)由此你能发现判定两直线平行的方法吗?
探索新知
(同位角相等,两直线平行)
讲解新知
平行线的判定方法:
2
∵∠1= ∠2
1
a
b
c
几何语言:
∴a∥b
两条直线被第三条直线所截, 如果同位角相等,那么这两条直线平行. 简单地说,同位角相等, 两直线平行.
练一练
如图,三根木条相交成∠1,∠2,固定木条b、c转动木条a , 猜一猜∠1,∠2满足什么条件时直线a与b平行.
当∠1=∠2时
直线a∥b
例题分析
如图,∠2+∠3=180°,
∴ ∠3=180°-∠2
=180°-135°
=45°
又∵ ∠1=45°,
∴ ∠1=∠3.
例1 如图,直线l1,l2 被l3所截,∠1=45°,
∠2=135°,试判断l1与l2是否平行.并说明理由.
1
2
解
∥ .理由如下:
∵ ∠1与∠3是直线l1,l2 被l3所截的一对同位角,
根据“同位角相等,两直线平行”,得l1 ∥l2.
3
例题分析
例2 如图,AB⊥EF,CD⊥EF,E,F分别为垂足.直线AB与CD平行吗?请说明理由.
解
∵ AB⊥EF,CD⊥EF,
∴ ∠1=∠2=Rt∠.
∴ AB∥CD
(根据什么?)
(同位角相等,两直线平行.)
A
B
C
D
E
F
“在同一平面 ,垂直于同一条直线的两条直线互相平行”.
课内练习
1
2
1.如图,直线l1,l2 被l3所截,且∠1=∠2.直线
l1与l2平行吗?请说明理由.
课内练习
2.某人骑自行车从A出发,沿正东方向前进至B处后,右转15°,沿直线向前行驶到C处(如图).这时他想仍按正东方向行驶,那么他应怎样调整行驶方向?请画出他继续行驶的路线,并说明理由.
A
B
C
15°
拓展提高
1.如图:AB⊥CD于点B,AE与BF相交于点G,且∠FGE=60°,∠ABG=30°,请判断AE与CD是否平行,并说明理由.
A
E
F
G
C
B
D
60°
30°
拓展提高
2.如图,已知∠ABD=∠ACE,BF、CG分别是∠ABD、∠ACE的平分线,请判断BF与CG是否平行,并说明理由.
A
B
C
D
E
F
G
解:
BF∥CG
1
2
∵BF、CG分别是∠ABD、∠ACE的平分线
∴ ∠1= ∠ABD,∠2= ∠ACE
∵
∠ABD =∠ACE
∴ ∠1=∠2
∴BF∥CG
(同位角相等,两直线平行)
3.甲,乙两船只分别从A、B两个港口出发,甲沿北偏东30度方向行驶,乙沿南偏西30度方向行驶,你知道甲船的航线与乙船的航线平行吗?为什么?
E
D
A
B
C
F
1
北
南
西
东
G
拓展提高
2
小结
1.判定两直线平行的方法:
同位角相等,两直线平行.
2.用“同位角相等,两直线平行”判定两直线平行.能进行简单的推理和表述.
再见
谢谢大家!
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
