1.3 平行线的判定(二) 课件(共21张PPT) 浙教版数学七年级下册
文档属性
| 名称 | 1.3 平行线的判定(二) 课件(共21张PPT) 浙教版数学七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 473.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 12:31:15 | ||
图片预览





文档简介
(共21张PPT)
浙教版七(下)
第一章 平行线
1.3 平行线的判定(二)
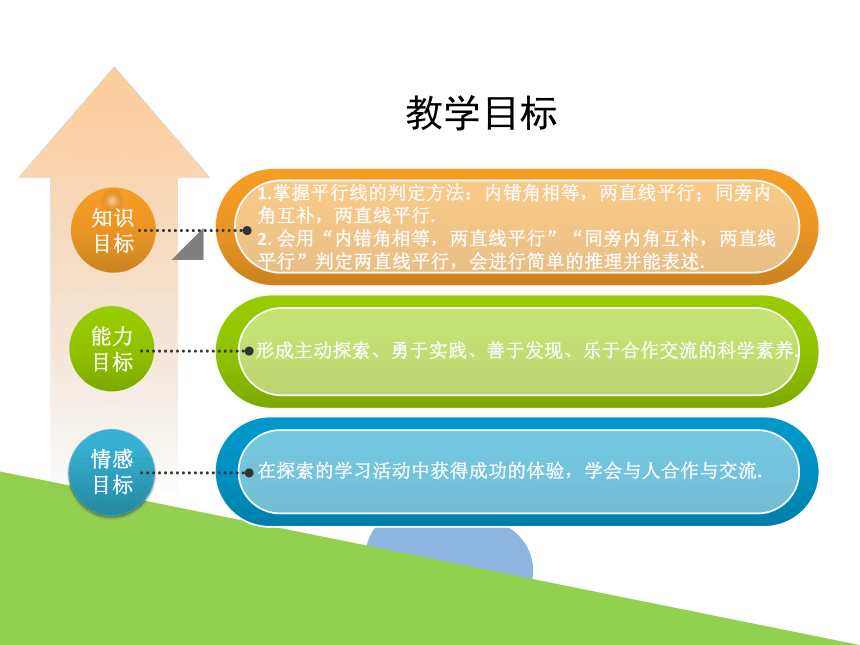
1.掌握平行线的判定方法:内错角相等,两直线平行;同旁内角互补,两直线平行.
2. 会用“内错角相等,两直线平行”“同旁内角互补,两直线平行”判定两直线平行,会进行简单的推理并能表述.
教学目标
形成主动探索、勇于实践、善于发现、乐于合作交流的科学素养.
在探索的学习活动中获得成功的体验,学会与人合作与交流.
知识目标
能力目标
情感目标
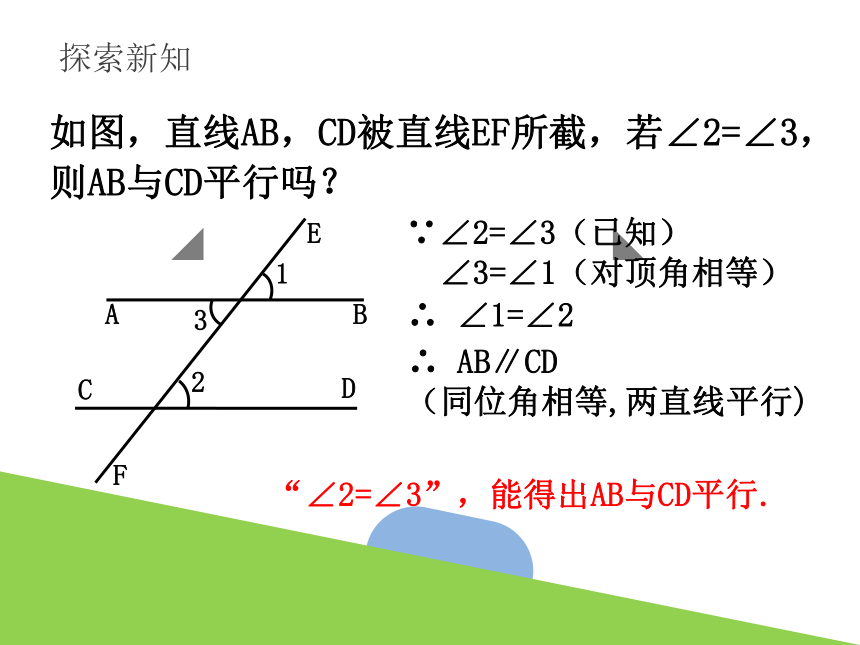
探索新知
∵∠2=∠3(已知)
∠3=∠1(对顶角相等)
∴ ∠1=∠2
∴ AB∥CD
(同位角相等,两直线平行)
B
3
A
C
D
F
1
2
E
如图,直线AB,CD被直线EF所截,若∠2=∠3,则AB与CD平行吗?
“∠2=∠3”,能得出AB与CD平行.
(内错角相等,两直线平行)
讲解新知
平行线的判定方法:
2
∵∠2=∠3
3
a
b
c
几何语言:
∴a∥b
两条直线被第三条直线所截, 如果内错角相等, 那么这两条直线平行. 简单地说,内错角相等, 两直线平行.
练一练
如图,已知∠1=121°,∠2 =120°,∠3=120°.说出其中的平行线,并说明理由.
1
2
3
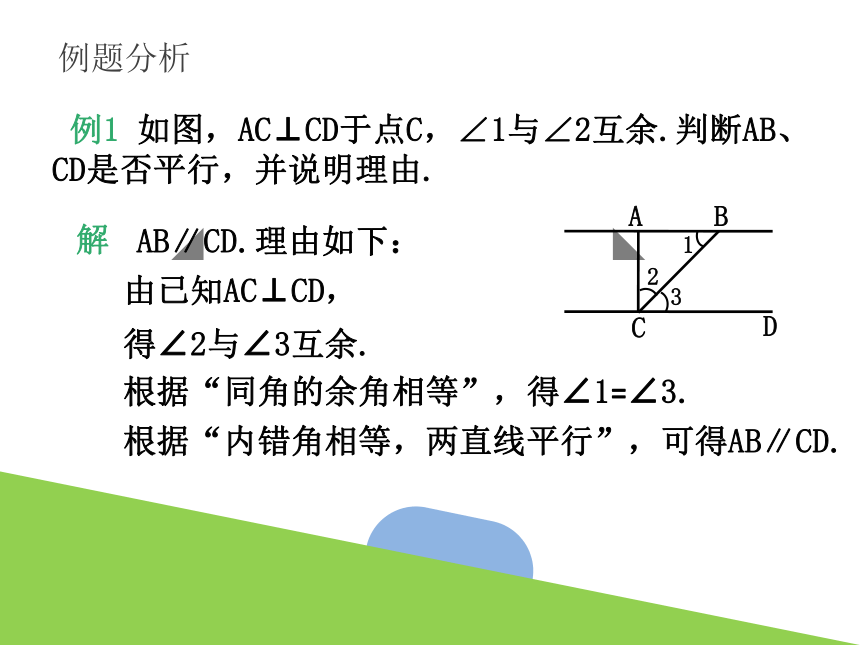
例题分析
例1 如图,AC⊥CD于点C,∠1与∠2互余.判断AB、CD是否平行,并说明理由.
解
AB∥CD.理由如下:
由已知AC⊥CD,
得∠2与∠3互余.
A
B
C
D
1
2
3
根据“同角的余角相等”,得∠1=∠3.
根据“内错角相等,两直线平行”,可得AB∥CD.
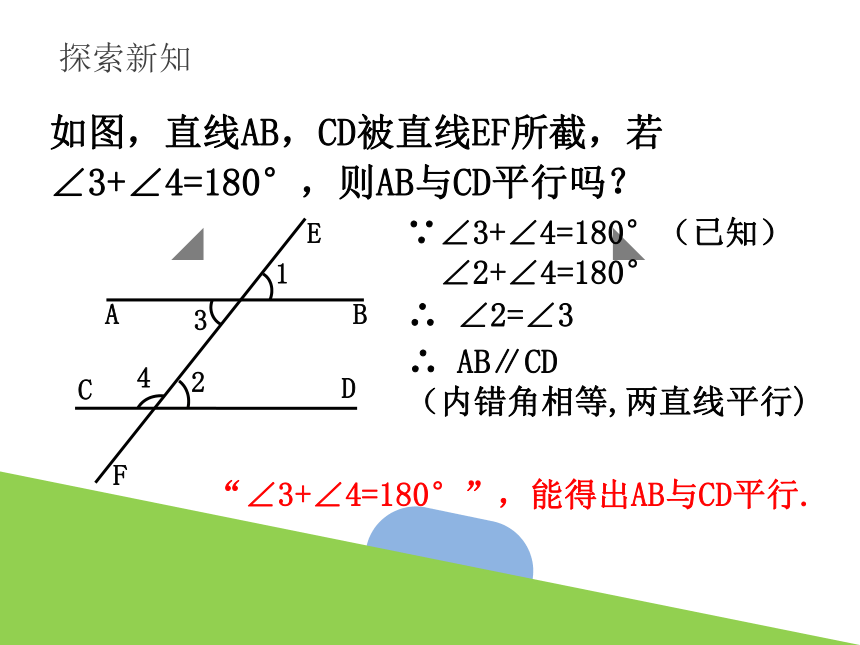
探索新知
∵∠3+∠4=180°(已知)
∠2+∠4=180°
∴ ∠2=∠3
∴ AB∥CD
(内错角相等,两直线平行)
B
3
A
C
D
F
1
2
E
如图,直线AB,CD被直线EF所截,若∠3+∠4=180°,则AB与CD平行吗?
“∠3+∠4=180°”,能得出AB与CD平行.
4
(同旁内角互补,两直线平行)
讲解新知
平行线的判定方法:
∵∠3+∠4=180°
3
a
b
c
几何语言:
∴a∥b
两条直线被第三条直线所截, 如果同旁内角互补, 那么这两条直线平行. 简单地说,同旁内角互补, 两直线平行.
4
例题分析
例2 如图,AP平分∠BAC,CE平分∠ACD,
∠1+∠2=90°,判断AB,CD是否平行,说明理由。
解
AB∥CD.
∴ AB∥CD.
A
B
C
D
P
1
2
∵AP平分∠BAC,CP平分∠ACD,
∴ ∠1= ∠BAC,
∠2= ∠ACD,
∴ ∠BAC+∠ACD=2(∠1+∠2)=2×90°=180°
(同旁内角互补,两直线平行)
课内练习
1.如图,
(1)从∠1=∠2,可以推出___∥___,
理由是_________________________.
(2)从∠2=∠___,可以推出c∥d,
理由是________________________.
(3)如果∠4=75°,∠3=75°,
可以推出___∥___.
(4) 从∠4=75°,∠5=_____°,
可以推出a∥b.
b
a
内错角相等,两直线平行
同位角相等,两直线平行
3
c
d
d
3
a
b
1
2
5
4
c
105
课内练习
2.如图,已知直线 , 被 所截,∠1+∠2=180°.。请说明 与 平行的理由.
1
2
探究活动
有一条线带如图所示.如果工具只有圆规,怎样检验纸带的两条边线是否平行?如果没有工具呢?请说出你的方法和依据.
拓展提高
1.有一块木板,怎样才能知道它上下边缘是否平行?
拓展提高
1.有一块木板,怎样才能知道它上下边缘是否平行?
1
2
1
2
拓展提高
1.有一块木板,怎样才能知道它上下边缘是否平行?
拓展提高
1.有一块木板,怎样才能知道它上下边缘是否平行?
1
2
拓展提高
2.如图,根据下列条件可判断哪两条直线平行,并说明理由.
A
B
C
D
1
2
3
4
(1)∠1=∠2
(2)∠3=∠A
(3)∠A+∠2+∠4=180°
拓展提高
1.如图,∠C=∠E+∠A,判断AB与CD是否平行,
并说明理由.
A
B
C
D
E
F
小结
1.同位角相等, 两直线平行.
2.内错角相等, 两直线平行.
3.同旁内角互补, 两直线平行.
4.在同一平面内,垂直于同一条直线的两直线平行.
判定两条直线平行的方法有:
再见
谢谢大家!
浙教版七(下)
第一章 平行线
1.3 平行线的判定(二)
1.掌握平行线的判定方法:内错角相等,两直线平行;同旁内角互补,两直线平行.
2. 会用“内错角相等,两直线平行”“同旁内角互补,两直线平行”判定两直线平行,会进行简单的推理并能表述.
教学目标
形成主动探索、勇于实践、善于发现、乐于合作交流的科学素养.
在探索的学习活动中获得成功的体验,学会与人合作与交流.
知识目标
能力目标
情感目标
探索新知
∵∠2=∠3(已知)
∠3=∠1(对顶角相等)
∴ ∠1=∠2
∴ AB∥CD
(同位角相等,两直线平行)
B
3
A
C
D
F
1
2
E
如图,直线AB,CD被直线EF所截,若∠2=∠3,则AB与CD平行吗?
“∠2=∠3”,能得出AB与CD平行.
(内错角相等,两直线平行)
讲解新知
平行线的判定方法:
2
∵∠2=∠3
3
a
b
c
几何语言:
∴a∥b
两条直线被第三条直线所截, 如果内错角相等, 那么这两条直线平行. 简单地说,内错角相等, 两直线平行.
练一练
如图,已知∠1=121°,∠2 =120°,∠3=120°.说出其中的平行线,并说明理由.
1
2
3
例题分析
例1 如图,AC⊥CD于点C,∠1与∠2互余.判断AB、CD是否平行,并说明理由.
解
AB∥CD.理由如下:
由已知AC⊥CD,
得∠2与∠3互余.
A
B
C
D
1
2
3
根据“同角的余角相等”,得∠1=∠3.
根据“内错角相等,两直线平行”,可得AB∥CD.
探索新知
∵∠3+∠4=180°(已知)
∠2+∠4=180°
∴ ∠2=∠3
∴ AB∥CD
(内错角相等,两直线平行)
B
3
A
C
D
F
1
2
E
如图,直线AB,CD被直线EF所截,若∠3+∠4=180°,则AB与CD平行吗?
“∠3+∠4=180°”,能得出AB与CD平行.
4
(同旁内角互补,两直线平行)
讲解新知
平行线的判定方法:
∵∠3+∠4=180°
3
a
b
c
几何语言:
∴a∥b
两条直线被第三条直线所截, 如果同旁内角互补, 那么这两条直线平行. 简单地说,同旁内角互补, 两直线平行.
4
例题分析
例2 如图,AP平分∠BAC,CE平分∠ACD,
∠1+∠2=90°,判断AB,CD是否平行,说明理由。
解
AB∥CD.
∴ AB∥CD.
A
B
C
D
P
1
2
∵AP平分∠BAC,CP平分∠ACD,
∴ ∠1= ∠BAC,
∠2= ∠ACD,
∴ ∠BAC+∠ACD=2(∠1+∠2)=2×90°=180°
(同旁内角互补,两直线平行)
课内练习
1.如图,
(1)从∠1=∠2,可以推出___∥___,
理由是_________________________.
(2)从∠2=∠___,可以推出c∥d,
理由是________________________.
(3)如果∠4=75°,∠3=75°,
可以推出___∥___.
(4) 从∠4=75°,∠5=_____°,
可以推出a∥b.
b
a
内错角相等,两直线平行
同位角相等,两直线平行
3
c
d
d
3
a
b
1
2
5
4
c
105
课内练习
2.如图,已知直线 , 被 所截,∠1+∠2=180°.。请说明 与 平行的理由.
1
2
探究活动
有一条线带如图所示.如果工具只有圆规,怎样检验纸带的两条边线是否平行?如果没有工具呢?请说出你的方法和依据.
拓展提高
1.有一块木板,怎样才能知道它上下边缘是否平行?
拓展提高
1.有一块木板,怎样才能知道它上下边缘是否平行?
1
2
1
2
拓展提高
1.有一块木板,怎样才能知道它上下边缘是否平行?
拓展提高
1.有一块木板,怎样才能知道它上下边缘是否平行?
1
2
拓展提高
2.如图,根据下列条件可判断哪两条直线平行,并说明理由.
A
B
C
D
1
2
3
4
(1)∠1=∠2
(2)∠3=∠A
(3)∠A+∠2+∠4=180°
拓展提高
1.如图,∠C=∠E+∠A,判断AB与CD是否平行,
并说明理由.
A
B
C
D
E
F
小结
1.同位角相等, 两直线平行.
2.内错角相等, 两直线平行.
3.同旁内角互补, 两直线平行.
4.在同一平面内,垂直于同一条直线的两直线平行.
判定两条直线平行的方法有:
再见
谢谢大家!
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
