2.4 二元一次方程组的应用 第一课时 课件(共16张PPT) 浙教版数学七年级下册
文档属性
| 名称 | 2.4 二元一次方程组的应用 第一课时 课件(共16张PPT) 浙教版数学七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
浙教版七(下)
第二章 二元一次方程组
2.4 二元一次方程组的应用(一)
1.了解列二元一次方程组与列一元一次方程的异同.
2.掌握应用二元一次方程组解决有关实际问题的基本步骤.
教学目标
1.会用二元一次方程组解决实际问题.
2.会用列表、画线段图等手段帮助分析理解实际问题,培养学生分析问题的能力.
经历和体验方程组解决实际问题的过程,发展学生的自主意识和初步养成善于分析问题的习惯.
知识目标
能力目标
情感目标
探索新知
游泳池中有一群小朋友,男孩戴蓝色游泳帽,女孩戴红色游泳帽.如果每位男孩看到蓝色与红色的游泳帽一样多,而每位女孩看到蓝色的游泳帽比红色的多1倍,你知道男孩与女孩各有多少人吗?
要解决这一问题,我们可以从以下几个方面进行思考:
(1)问题中所求的未知数有几个?
(2)有哪些等量关系?
(3)怎样设未知数?可以列出几个方程?
(4)本题能列一元一次方程求解吗?用列二元一次方程组的方法求解,有什么优点?
讲解新知
用两个字母来表示未知数往往比较容易列出方程.要注意的是必须寻找两个等量关系,列出两个不同的方程组成二元一次方程组.
例题分析
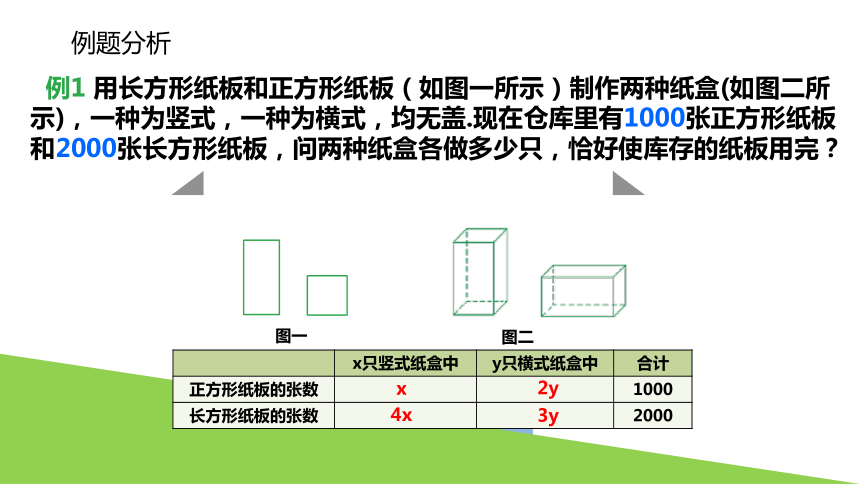
例1 用长方形纸板和正方形纸板(如图一所示)制作两种纸盒(如图二所示),一种为竖式,一种为横式,均无盖.现在仓库里有1000张正方形纸板和2000张长方形纸板,问两种纸盒各做多少只,恰好使库存的纸板用完?
图一
图二
x只竖式纸盒中 y只横式纸盒中 合计
正方形纸板的张数 1000
长方形纸板的张数 2000
x
2y
4x
3y
例题分析
x只竖式纸盒中 y只横式纸盒中 合计
正方形纸板的张数 1000
长方形纸板的张数 2000
x
2y
4x
3y
解
设做竖式纸盒x个,横式纸盒y个.根据题意,得
①
②
①×4-②,
得5y=2000,解得y=400.
把y=400代入①,
得x+800=1000,
解得x=200.
所以方程组的解为
经检验,这个解满足方程组,且符合题意.
答:做竖式纸盒200个,横式纸盒400个,恰好将库存的纸板用完.
上题中如果改为库存正方形纸板500张,长方形纸板1001张,那么,能否做成若干只竖式纸盒和若干只横式纸盒后,恰好把库存纸板用完?
变式一
图一
图二
x只竖式纸盒中 y只横式纸盒中 合计
正方形纸板的张数 500
长方形纸板的张数 1001
x
2y
4x
3y
例题分析
解 设做竖式纸盒x个,做横式纸盒y个,根据题意,得
x、y不是自然数,不合题意,所以不可能做成若干个纸盒,恰好把库存的纸板用完.
解得
例题分析
x只竖式纸盒中 y只横式纸盒中 合计
正方形纸板的张数 500
长方形纸板的张数 1001
x
2y
4x
3y
讲解新知
二元一次方程组解决实际问题的基本步骤有哪些?
1.理解问题(审题,搞清已知和未知,分析数量关系)
2.制订计划(考虑如何根据等量关系设元,列出方程组)
3.执行计划(列出方程组并求解,得到答案)
4.回 顾(检查和反思解题过程,检验答案的正确性以及是否符合题意)
课内练习
甲、乙两人从相距36千米的两地匀速相向而行.如果甲比乙先走2小时,那么他们在乙出发后经2.5小时相遇;如果乙比甲先走2小时,那么他们在甲出发后经3小时相遇.请分析题中的等量关系,你会用示意图表示数量关系吗?甲乙两人每小时各走多少千米?
1.甲、乙两人从相距18千米的两地同时出发,相向而行,经9/5时相遇.如果甲比乙先出发2/3时,那么在乙出发后经3/2时两人相遇.求甲、乙两人速度.
等量关系:
甲行9/5时的路程 +乙行9/5时的路程=18千米
甲行2/3时的路程+甲行3/2时的路程
+乙行3/2时的路程=18千米
拓展提高
2.某工地派96人去挖土和运土.如果平均每人每天挖土5m3或运土3m3,那么怎样分配挖土和运土的人数,才能使挖出的土刚好能被运完?
挖土人数 + 运土人数 = 96人
设挖土人数x人,运土人数y人,由题意得:
x + y = 96
5 x = 3y
等量关系:
挖出的土的体积 = 运出的土的体积
方程:
拓展提高
2.一船队运送一批货物,如果每艘船装50吨,还剩下25吨装不完;如果每艘船再多装5吨,还有35吨空位.求这个船队共有多少艘船,共有货物多少吨?
55×船数-35=货物数量
等量关系:
50×船数+25=货物数量
拓展提高
小结
2.借助列表、线段图等分析题意,找出题中的等量关系.
1.应用二元一次方程组解决实际问题的基本步骤.
再见
谢谢大家!
浙教版七(下)
第二章 二元一次方程组
2.4 二元一次方程组的应用(一)
1.了解列二元一次方程组与列一元一次方程的异同.
2.掌握应用二元一次方程组解决有关实际问题的基本步骤.
教学目标
1.会用二元一次方程组解决实际问题.
2.会用列表、画线段图等手段帮助分析理解实际问题,培养学生分析问题的能力.
经历和体验方程组解决实际问题的过程,发展学生的自主意识和初步养成善于分析问题的习惯.
知识目标
能力目标
情感目标
探索新知
游泳池中有一群小朋友,男孩戴蓝色游泳帽,女孩戴红色游泳帽.如果每位男孩看到蓝色与红色的游泳帽一样多,而每位女孩看到蓝色的游泳帽比红色的多1倍,你知道男孩与女孩各有多少人吗?
要解决这一问题,我们可以从以下几个方面进行思考:
(1)问题中所求的未知数有几个?
(2)有哪些等量关系?
(3)怎样设未知数?可以列出几个方程?
(4)本题能列一元一次方程求解吗?用列二元一次方程组的方法求解,有什么优点?
讲解新知
用两个字母来表示未知数往往比较容易列出方程.要注意的是必须寻找两个等量关系,列出两个不同的方程组成二元一次方程组.
例题分析
例1 用长方形纸板和正方形纸板(如图一所示)制作两种纸盒(如图二所示),一种为竖式,一种为横式,均无盖.现在仓库里有1000张正方形纸板和2000张长方形纸板,问两种纸盒各做多少只,恰好使库存的纸板用完?
图一
图二
x只竖式纸盒中 y只横式纸盒中 合计
正方形纸板的张数 1000
长方形纸板的张数 2000
x
2y
4x
3y
例题分析
x只竖式纸盒中 y只横式纸盒中 合计
正方形纸板的张数 1000
长方形纸板的张数 2000
x
2y
4x
3y
解
设做竖式纸盒x个,横式纸盒y个.根据题意,得
①
②
①×4-②,
得5y=2000,解得y=400.
把y=400代入①,
得x+800=1000,
解得x=200.
所以方程组的解为
经检验,这个解满足方程组,且符合题意.
答:做竖式纸盒200个,横式纸盒400个,恰好将库存的纸板用完.
上题中如果改为库存正方形纸板500张,长方形纸板1001张,那么,能否做成若干只竖式纸盒和若干只横式纸盒后,恰好把库存纸板用完?
变式一
图一
图二
x只竖式纸盒中 y只横式纸盒中 合计
正方形纸板的张数 500
长方形纸板的张数 1001
x
2y
4x
3y
例题分析
解 设做竖式纸盒x个,做横式纸盒y个,根据题意,得
x、y不是自然数,不合题意,所以不可能做成若干个纸盒,恰好把库存的纸板用完.
解得
例题分析
x只竖式纸盒中 y只横式纸盒中 合计
正方形纸板的张数 500
长方形纸板的张数 1001
x
2y
4x
3y
讲解新知
二元一次方程组解决实际问题的基本步骤有哪些?
1.理解问题(审题,搞清已知和未知,分析数量关系)
2.制订计划(考虑如何根据等量关系设元,列出方程组)
3.执行计划(列出方程组并求解,得到答案)
4.回 顾(检查和反思解题过程,检验答案的正确性以及是否符合题意)
课内练习
甲、乙两人从相距36千米的两地匀速相向而行.如果甲比乙先走2小时,那么他们在乙出发后经2.5小时相遇;如果乙比甲先走2小时,那么他们在甲出发后经3小时相遇.请分析题中的等量关系,你会用示意图表示数量关系吗?甲乙两人每小时各走多少千米?
1.甲、乙两人从相距18千米的两地同时出发,相向而行,经9/5时相遇.如果甲比乙先出发2/3时,那么在乙出发后经3/2时两人相遇.求甲、乙两人速度.
等量关系:
甲行9/5时的路程 +乙行9/5时的路程=18千米
甲行2/3时的路程+甲行3/2时的路程
+乙行3/2时的路程=18千米
拓展提高
2.某工地派96人去挖土和运土.如果平均每人每天挖土5m3或运土3m3,那么怎样分配挖土和运土的人数,才能使挖出的土刚好能被运完?
挖土人数 + 运土人数 = 96人
设挖土人数x人,运土人数y人,由题意得:
x + y = 96
5 x = 3y
等量关系:
挖出的土的体积 = 运出的土的体积
方程:
拓展提高
2.一船队运送一批货物,如果每艘船装50吨,还剩下25吨装不完;如果每艘船再多装5吨,还有35吨空位.求这个船队共有多少艘船,共有货物多少吨?
55×船数-35=货物数量
等量关系:
50×船数+25=货物数量
拓展提高
小结
2.借助列表、线段图等分析题意,找出题中的等量关系.
1.应用二元一次方程组解决实际问题的基本步骤.
再见
谢谢大家!
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
