2.4 二元一次方程组的应用 第二课时 课件(共20张PPT) 浙教版数学七年级下册
文档属性
| 名称 | 2.4 二元一次方程组的应用 第二课时 课件(共20张PPT) 浙教版数学七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 615.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
浙教版七(下)
第二章 二元一次方程组
2.4 二元一次方程组的应用(二)
了解解二元一次方程组的基本思想是消元,化二元为一元;了解加减消元法解二元一次方程组的一般步骤.
教学目标
会用加减消元法解二元一次方程组,初步形成用便捷的消元法(即加减法和代入法)来解题.
使学生理解加减消元法的基本思想所体现的“化未知为已知”的化归思想方法.
知识目标
能力目标
情感目标
知识回顾
二元一次方程组解决实际问题的基本步骤:
1.理解问题(审题,搞清已知和未知,分析数量关系)
2.制订计划(考虑如何根据等量关系设元,列出方程组)
3.执行计划(列出方程组并求解,得到答案)
4.回 顾(检查和反思解题过程,检验答案的正确性以及是否符合题意)
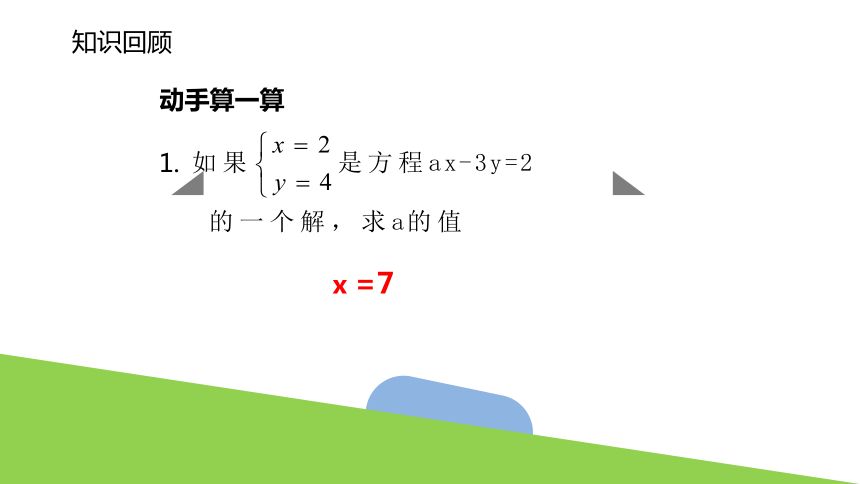
动手算一算
1.
x =7
知识回顾
动手算一算
2. 已知二元一次方程ax+by=10的两个解为
x = -1 x = 1
y = 0 y = 5
则a = ______, b = _______.
- 10
4
知识回顾
一根金属棒在0℃时的长度是q(m),温度每升高1℃,它就伸长p(m).当温度为t(℃)时,金属棒的长度L可用公式L=pt+q计算.已测得当t=100℃时,L=2.002m;当t=500℃时,L=2.01m.
(1)求p,q的值;
(2)若这根金属棒加热后长度伸长到2.016m,
问这时金属棒的温度是多少
例题分析
例1
(1)根据题意得:
100p+q=2.002 ①
500p+q=2.01 ②
②-①, 400p=0.008,
解得:p=0.00002.
把P=0.00002代入①,得 0.002+q=2.002,解得q=2
p=0.00002
q=2
即
解
待定系数法
一根金属棒在0℃时的长度是q(m),温度每升高1℃,它就伸长p(m).当温度为t(℃)时,金属棒的长度L可用公式L=pt+q计算.已测得当t=100℃时,L=2.002m;当t=500℃时,L=2.01m.
(1)求p,q的值;
(2)若这根金属棒加热后长度伸长到2.016m,
问这时金属棒的温度是多少
例题分析
例1
(2) 由(1),得 L=0.00002t+2
金属棒加热后,长度伸长到2.016m,即当L=2.016时, 2.016=0.00002t+2
答:此时金属棒的温度是800℃
解得这个一元一次方程,得t=800℃
解
例题分析
例3 通过对一份中学生营养快餐的检测,得到以下信息:
(1)快餐总质量为300g;
(2)快餐的成分:蛋白质、碳水化合物、脂肪、矿物质;
(3)蛋白质和脂肪含量占50%;矿物质的含量是脂肪含量的2倍;蛋白质和碳水化合物含量占85%.
根据上述数据回答下面的问题:
试分别求出营养快餐中蛋白质、碳水化合物、脂肪、矿物质的质量和所占百分比;
x
y
(300×85%-x)
2y
蛋白质
碳水化合物
脂肪
矿物质
快餐的成分:
85%
例题分析
x
y
(300×85%-x)
2y
蛋白质
碳水化合物
脂肪
矿物质
快餐的成分:
50%
50%
设蛋白质有xg,脂肪有yg,
则矿物质物有2yg,
碳水化合物有(300×85% -x)g.
x+y=300×50% (300×85% -x)+2y=300×50%
解
化简,得
x+y=150
-x+2y=-105
①
②
①+②,得3y=45,解得y=15.
∴x=150-y=150-15=135(g),
2y=2×15=30(g),
300×85%-x=225-135=120(g).
例题分析
答:营养快餐中蛋白质、碳水化合物、脂肪、矿物质的质量和所占的百分比比如下表.
蛋白质 脂肪 矿物质 碳水化合物 合计
各种成分的质量(g) 135 15 30 120 300
各种成分所占的百分比(%) 45 5 10 40 100
中学生营养快餐成分扇形统计图
蛋白质
碳水化合物
脂肪
矿物质
课内练习
解得:
x=25
y=20
答:种粮食25公顷,种蔬菜20公顷.
1.某村有土地58公顷,计划将12公顷山坡地开辟为茶园,其余的土地种植粮食和蔬菜。已知种粮食的土地面积是种蔬菜的 倍,问计划种植粮食和蔬菜的土地面积各多少公顷?
等量关系:茶园+粮食+蔬菜=总土地面积;
种粮食=种蔬菜×
解:设种粮食x公顷,种蔬菜y公顷.
x+y+12 = 58
x = y
课内练习
摩托车 公交车 货车 小汽车 合 计
7:50~8:00 7 12 44
8:00~8:10 7 8 40
合 计 30 20 20
2.下表是小红在2003年下旬制作的一份统计表,其中空格处的字迹已模糊不清,但小红还记得7:50~8:00时段内的摩托车辆数与8:00~8:10时段内的货车辆数之比是5:4.根据这些数据,你能把这分统计表填完整吗
等量关系:7:50~8:00摩托车: 8:00~8:10=5:4
摩托+公交+货车+小汽车=总辆数
x
y
20-y
2012年6月23日东胜路7:50~8:10经过车辆统计表(单位:辆)
30-x
14
84
课内练习
摩托车 公交车 货车 小汽车 合 计
7:50~8:00 7 12 44
8:00~8:10 7 8 40
合 计 30 20 20
2.下表是小红在2003年下旬制作的一份统计表,其中空格处的字迹已模糊不清,但小红还记得7:50~8:00时段内的摩托车辆数与8:00~8:10时段内的货车辆数之比是5:4.根据这些数据,你能把这分统计表填完整吗
x
y
20-y
2012年6月23日东胜路7:50~8:10经过车辆统计表(单位:辆)
30-x
14
84
x:y=5:4
5y=4x
x+7+20-y+12=44
解得
x=25
y=20
课内练习
摩托车 公交车 货车 小汽车 合 计
7:50~8:00 7 12 44
8:00~8:10 7 8 40
合 计 30 20 20
2.下表是小红在2003年下旬制作的一份统计表,其中空格处的字迹已模糊不清,但小红还记得7:50~8:00时段内的摩托车辆数与8:00~8:10时段内的货车辆数之比是5:4.根据这些数据,你能把这分统计表填完整吗
25
20
0
2012年6月23日东胜路7:50~8:10经过车辆统计表(单位:辆)
5
14
84
x:y=5:4
5y=4x
x+7+20-y+12=44
解得
x=25
y=20
1.某校教师举行茶话会,若每桌坐12人,则空出一张桌子;若每桌坐10人,还有10人不能就坐.问该校有多少名教师?共准备了多少张桌子?
等量关系:每桌人数12人×(桌数-1)=总人数;
每桌人数10人× 桌数+10人=总人数.
解:设该校有x名教师,共准备了y张桌子.
12(y-1)= x
10y+10= x
解得:
x=120
y=11
答:该校有120名教师,共准备了11张桌子.
拓展提高
拓展提高
2.声音在空气中传播的速度随温度的变化而变化,科学家已测得一定的温度下声音传播的速度如左表.若用v表示声音在空气中的传播速度,t表示温度,则满足公式:v=at+b(a,b为已知数),求a,b的值,并求当t=15℃时,v的值.
解:由题意得,当t=o℃时,v=330米/秒;当t=10℃时,v=336米/秒,代入v=at+b,得
0×a+b=330
10a+b=336
a=0.6
b=330
解得
即:v=0.6t+330
当t=15℃时,v=0.6×15+330
=339(米/秒)
气 温 (℃) 声音的传播速度(米/秒)
-20 318
-10 324
0 330
10 336
20 342
30 348
拓展提高
3.一条铁路线A,B,C三个车站的位置如图所示.已知B,C两车站之间相距520千米.火车从B站出发,向C站方向匀速行驶,经过30分,距A站150千米;经过2时,距A站345千米.问火车从B站开出,多少时间后可到达C站?
A
B
C
150km
A
B
C
345km
y
经过30分
y
经过2时
y+0.5x=150
解:设火车的速度为xkm/h,A,B两站的路程为ykm
y+2x=345
小结
实际问题
分析
转化
方程(组)
求解
检验
问题解决
生活问题数学化,数学问题生活化
再见
谢谢大家!
浙教版七(下)
第二章 二元一次方程组
2.4 二元一次方程组的应用(二)
了解解二元一次方程组的基本思想是消元,化二元为一元;了解加减消元法解二元一次方程组的一般步骤.
教学目标
会用加减消元法解二元一次方程组,初步形成用便捷的消元法(即加减法和代入法)来解题.
使学生理解加减消元法的基本思想所体现的“化未知为已知”的化归思想方法.
知识目标
能力目标
情感目标
知识回顾
二元一次方程组解决实际问题的基本步骤:
1.理解问题(审题,搞清已知和未知,分析数量关系)
2.制订计划(考虑如何根据等量关系设元,列出方程组)
3.执行计划(列出方程组并求解,得到答案)
4.回 顾(检查和反思解题过程,检验答案的正确性以及是否符合题意)
动手算一算
1.
x =7
知识回顾
动手算一算
2. 已知二元一次方程ax+by=10的两个解为
x = -1 x = 1
y = 0 y = 5
则a = ______, b = _______.
- 10
4
知识回顾
一根金属棒在0℃时的长度是q(m),温度每升高1℃,它就伸长p(m).当温度为t(℃)时,金属棒的长度L可用公式L=pt+q计算.已测得当t=100℃时,L=2.002m;当t=500℃时,L=2.01m.
(1)求p,q的值;
(2)若这根金属棒加热后长度伸长到2.016m,
问这时金属棒的温度是多少
例题分析
例1
(1)根据题意得:
100p+q=2.002 ①
500p+q=2.01 ②
②-①, 400p=0.008,
解得:p=0.00002.
把P=0.00002代入①,得 0.002+q=2.002,解得q=2
p=0.00002
q=2
即
解
待定系数法
一根金属棒在0℃时的长度是q(m),温度每升高1℃,它就伸长p(m).当温度为t(℃)时,金属棒的长度L可用公式L=pt+q计算.已测得当t=100℃时,L=2.002m;当t=500℃时,L=2.01m.
(1)求p,q的值;
(2)若这根金属棒加热后长度伸长到2.016m,
问这时金属棒的温度是多少
例题分析
例1
(2) 由(1),得 L=0.00002t+2
金属棒加热后,长度伸长到2.016m,即当L=2.016时, 2.016=0.00002t+2
答:此时金属棒的温度是800℃
解得这个一元一次方程,得t=800℃
解
例题分析
例3 通过对一份中学生营养快餐的检测,得到以下信息:
(1)快餐总质量为300g;
(2)快餐的成分:蛋白质、碳水化合物、脂肪、矿物质;
(3)蛋白质和脂肪含量占50%;矿物质的含量是脂肪含量的2倍;蛋白质和碳水化合物含量占85%.
根据上述数据回答下面的问题:
试分别求出营养快餐中蛋白质、碳水化合物、脂肪、矿物质的质量和所占百分比;
x
y
(300×85%-x)
2y
蛋白质
碳水化合物
脂肪
矿物质
快餐的成分:
85%
例题分析
x
y
(300×85%-x)
2y
蛋白质
碳水化合物
脂肪
矿物质
快餐的成分:
50%
50%
设蛋白质有xg,脂肪有yg,
则矿物质物有2yg,
碳水化合物有(300×85% -x)g.
x+y=300×50% (300×85% -x)+2y=300×50%
解
化简,得
x+y=150
-x+2y=-105
①
②
①+②,得3y=45,解得y=15.
∴x=150-y=150-15=135(g),
2y=2×15=30(g),
300×85%-x=225-135=120(g).
例题分析
答:营养快餐中蛋白质、碳水化合物、脂肪、矿物质的质量和所占的百分比比如下表.
蛋白质 脂肪 矿物质 碳水化合物 合计
各种成分的质量(g) 135 15 30 120 300
各种成分所占的百分比(%) 45 5 10 40 100
中学生营养快餐成分扇形统计图
蛋白质
碳水化合物
脂肪
矿物质
课内练习
解得:
x=25
y=20
答:种粮食25公顷,种蔬菜20公顷.
1.某村有土地58公顷,计划将12公顷山坡地开辟为茶园,其余的土地种植粮食和蔬菜。已知种粮食的土地面积是种蔬菜的 倍,问计划种植粮食和蔬菜的土地面积各多少公顷?
等量关系:茶园+粮食+蔬菜=总土地面积;
种粮食=种蔬菜×
解:设种粮食x公顷,种蔬菜y公顷.
x+y+12 = 58
x = y
课内练习
摩托车 公交车 货车 小汽车 合 计
7:50~8:00 7 12 44
8:00~8:10 7 8 40
合 计 30 20 20
2.下表是小红在2003年下旬制作的一份统计表,其中空格处的字迹已模糊不清,但小红还记得7:50~8:00时段内的摩托车辆数与8:00~8:10时段内的货车辆数之比是5:4.根据这些数据,你能把这分统计表填完整吗
等量关系:7:50~8:00摩托车: 8:00~8:10=5:4
摩托+公交+货车+小汽车=总辆数
x
y
20-y
2012年6月23日东胜路7:50~8:10经过车辆统计表(单位:辆)
30-x
14
84
课内练习
摩托车 公交车 货车 小汽车 合 计
7:50~8:00 7 12 44
8:00~8:10 7 8 40
合 计 30 20 20
2.下表是小红在2003年下旬制作的一份统计表,其中空格处的字迹已模糊不清,但小红还记得7:50~8:00时段内的摩托车辆数与8:00~8:10时段内的货车辆数之比是5:4.根据这些数据,你能把这分统计表填完整吗
x
y
20-y
2012年6月23日东胜路7:50~8:10经过车辆统计表(单位:辆)
30-x
14
84
x:y=5:4
5y=4x
x+7+20-y+12=44
解得
x=25
y=20
课内练习
摩托车 公交车 货车 小汽车 合 计
7:50~8:00 7 12 44
8:00~8:10 7 8 40
合 计 30 20 20
2.下表是小红在2003年下旬制作的一份统计表,其中空格处的字迹已模糊不清,但小红还记得7:50~8:00时段内的摩托车辆数与8:00~8:10时段内的货车辆数之比是5:4.根据这些数据,你能把这分统计表填完整吗
25
20
0
2012年6月23日东胜路7:50~8:10经过车辆统计表(单位:辆)
5
14
84
x:y=5:4
5y=4x
x+7+20-y+12=44
解得
x=25
y=20
1.某校教师举行茶话会,若每桌坐12人,则空出一张桌子;若每桌坐10人,还有10人不能就坐.问该校有多少名教师?共准备了多少张桌子?
等量关系:每桌人数12人×(桌数-1)=总人数;
每桌人数10人× 桌数+10人=总人数.
解:设该校有x名教师,共准备了y张桌子.
12(y-1)= x
10y+10= x
解得:
x=120
y=11
答:该校有120名教师,共准备了11张桌子.
拓展提高
拓展提高
2.声音在空气中传播的速度随温度的变化而变化,科学家已测得一定的温度下声音传播的速度如左表.若用v表示声音在空气中的传播速度,t表示温度,则满足公式:v=at+b(a,b为已知数),求a,b的值,并求当t=15℃时,v的值.
解:由题意得,当t=o℃时,v=330米/秒;当t=10℃时,v=336米/秒,代入v=at+b,得
0×a+b=330
10a+b=336
a=0.6
b=330
解得
即:v=0.6t+330
当t=15℃时,v=0.6×15+330
=339(米/秒)
气 温 (℃) 声音的传播速度(米/秒)
-20 318
-10 324
0 330
10 336
20 342
30 348
拓展提高
3.一条铁路线A,B,C三个车站的位置如图所示.已知B,C两车站之间相距520千米.火车从B站出发,向C站方向匀速行驶,经过30分,距A站150千米;经过2时,距A站345千米.问火车从B站开出,多少时间后可到达C站?
A
B
C
150km
A
B
C
345km
y
经过30分
y
经过2时
y+0.5x=150
解:设火车的速度为xkm/h,A,B两站的路程为ykm
y+2x=345
小结
实际问题
分析
转化
方程(组)
求解
检验
问题解决
生活问题数学化,数学问题生活化
再见
谢谢大家!
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
