4.3《用乘法公式分解因式》第一课时 课件(共20张PPT) 浙教版数学七年级下册
文档属性
| 名称 | 4.3《用乘法公式分解因式》第一课时 课件(共20张PPT) 浙教版数学七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 333.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 12:29:20 | ||
图片预览








文档简介
(共20张PPT)
用乘法公式分解因式(1)
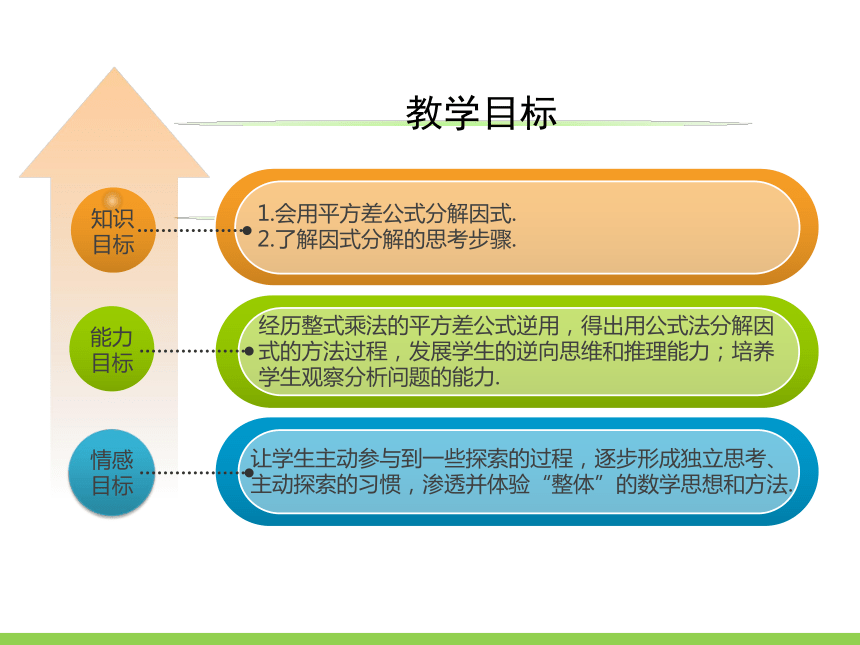
1.会用平方差公式分解因式.
2.了解因式分解的思考步骤.
教学目标
经历整式乘法的平方差公式逆用,得出用公式法分解因式的方法过程,发展学生的逆向思维和推理能力;培养学生观察分析问题的能力.
让学生主动参与到一些探索的过程,逐步形成独立思考、主动探索的习惯,渗透并体验“整体”的数学思想和方法.
知识目标
能力目标
情感目标
知识回顾
下列等式中,哪些是因式分解?哪些不是?为什么?
一个多项式
几个整式的积
有一个必定是多项式
最后一步运算是乘法
知识回顾
练一练:分解因式
公因式:
提取公因式法的一般步骤:
(1)确定应提取的公因式
(2)多项式除以公因式,所得的商作为另一个因式
(3)把多项式写成这两个因式的积的形式
×
各项都含有的相同字母的最低次幂
各项系数的最大公因数
讲解新知
两个数的平方差=这两个数的和与这两个数的差的积.
两个数的和与这两个数的差的积=这两个数的平方差.
都叫作平方差公式
整式乘法:
因式分解:
做一做
下列各式能用平方差公式 分解因式吗? 分别表示什么?
只有符合平方差公式的特征,才可以用平方差公式分解.
练一练
(1)公式左边:
(是一个将要被分解因式的多项式)
★被分解的多项式含有两项,且这两项异号,并且能写成( )2-( )2的形式。
)
)(
(
2
2
b
a
b
a
b
a
-
+
=
-
▲
▲
▲
练一练
下列多项式能转化成( )2-( )2的形式吗?如果能,请将其转化成( )2-( )2的形式.
(1) m2 -1
(2)4m2 -9
(3)4m2+9
(4)x2 -25y 2
(5) -x2 -25y2
(6) -x2+25y2
=m2 -12
=(2m)2 -32
不能转化为平方差形式
=x2 -(5y)2
不能转化为平方差形式
= 25y2-x2 =(5y)2 -x2
a2 - b2= (a + b) (a - b)
例题分析
例1 把 分解因式.
解
添括号
括号前面是“+”号,括到括号里的各项都不变号;括号前面是“-”号,括到括号里的各项都变号.
讲解新知
参照对象:
)
)(
(
2
2
b
a
b
a
b
a
-
+
=
-
20062-20052 =
(2mn)2 - ( 3xy)2 =
(n+2)2 - (n-3)2 =
结论:
公式中的a、b无论表示数、单项式、还是多项式,只要被分解的多项式能转化成平方差的形式,就能用平方差公式因式分解.
例题分析
例2 把下列各式分解因式:
练一练
分解因式:
(2)因式分解要彻底,直到不能分解为止.
(1)因式分解时,通常先考虑提取公因式法,然后再考虑其他法.
注意:
例题分析
例3 分解因式:
解
课内练习
1.分解因式:
课内练习
2.下列多项式可以用平方差公式分解因式吗?说说你的理由.
课内练习
3.分解因式:
拓展提高
分解因式:
先提取公因式,后用平方差公式
两次运用平方差公式
小结
(1)形如________形式的多项式可以用平方差公式分解因式.
(3)因式分解要______.
(2)因式分解通常先考虑______________方法.
提取公因式法
彻底
随 堂 作 业
再见
谢谢大家!
用乘法公式分解因式(1)
1.会用平方差公式分解因式.
2.了解因式分解的思考步骤.
教学目标
经历整式乘法的平方差公式逆用,得出用公式法分解因式的方法过程,发展学生的逆向思维和推理能力;培养学生观察分析问题的能力.
让学生主动参与到一些探索的过程,逐步形成独立思考、主动探索的习惯,渗透并体验“整体”的数学思想和方法.
知识目标
能力目标
情感目标
知识回顾
下列等式中,哪些是因式分解?哪些不是?为什么?
一个多项式
几个整式的积
有一个必定是多项式
最后一步运算是乘法
知识回顾
练一练:分解因式
公因式:
提取公因式法的一般步骤:
(1)确定应提取的公因式
(2)多项式除以公因式,所得的商作为另一个因式
(3)把多项式写成这两个因式的积的形式
×
各项都含有的相同字母的最低次幂
各项系数的最大公因数
讲解新知
两个数的平方差=这两个数的和与这两个数的差的积.
两个数的和与这两个数的差的积=这两个数的平方差.
都叫作平方差公式
整式乘法:
因式分解:
做一做
下列各式能用平方差公式 分解因式吗? 分别表示什么?
只有符合平方差公式的特征,才可以用平方差公式分解.
练一练
(1)公式左边:
(是一个将要被分解因式的多项式)
★被分解的多项式含有两项,且这两项异号,并且能写成( )2-( )2的形式。
)
)(
(
2
2
b
a
b
a
b
a
-
+
=
-
▲
▲
▲
练一练
下列多项式能转化成( )2-( )2的形式吗?如果能,请将其转化成( )2-( )2的形式.
(1) m2 -1
(2)4m2 -9
(3)4m2+9
(4)x2 -25y 2
(5) -x2 -25y2
(6) -x2+25y2
=m2 -12
=(2m)2 -32
不能转化为平方差形式
=x2 -(5y)2
不能转化为平方差形式
= 25y2-x2 =(5y)2 -x2
a2 - b2= (a + b) (a - b)
例题分析
例1 把 分解因式.
解
添括号
括号前面是“+”号,括到括号里的各项都不变号;括号前面是“-”号,括到括号里的各项都变号.
讲解新知
参照对象:
)
)(
(
2
2
b
a
b
a
b
a
-
+
=
-
20062-20052 =
(2mn)2 - ( 3xy)2 =
(n+2)2 - (n-3)2 =
结论:
公式中的a、b无论表示数、单项式、还是多项式,只要被分解的多项式能转化成平方差的形式,就能用平方差公式因式分解.
例题分析
例2 把下列各式分解因式:
练一练
分解因式:
(2)因式分解要彻底,直到不能分解为止.
(1)因式分解时,通常先考虑提取公因式法,然后再考虑其他法.
注意:
例题分析
例3 分解因式:
解
课内练习
1.分解因式:
课内练习
2.下列多项式可以用平方差公式分解因式吗?说说你的理由.
课内练习
3.分解因式:
拓展提高
分解因式:
先提取公因式,后用平方差公式
两次运用平方差公式
小结
(1)形如________形式的多项式可以用平方差公式分解因式.
(3)因式分解要______.
(2)因式分解通常先考虑______________方法.
提取公因式法
彻底
随 堂 作 业
再见
谢谢大家!
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
