5.1 分式 课件(共13张PPT) 浙教版数学七年级下册
文档属性
| 名称 | 5.1 分式 课件(共13张PPT) 浙教版数学七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 12:44:49 | ||
图片预览





文档简介
(共13张PPT)
浙教版七(下)
第五章 分式
5.1 分式
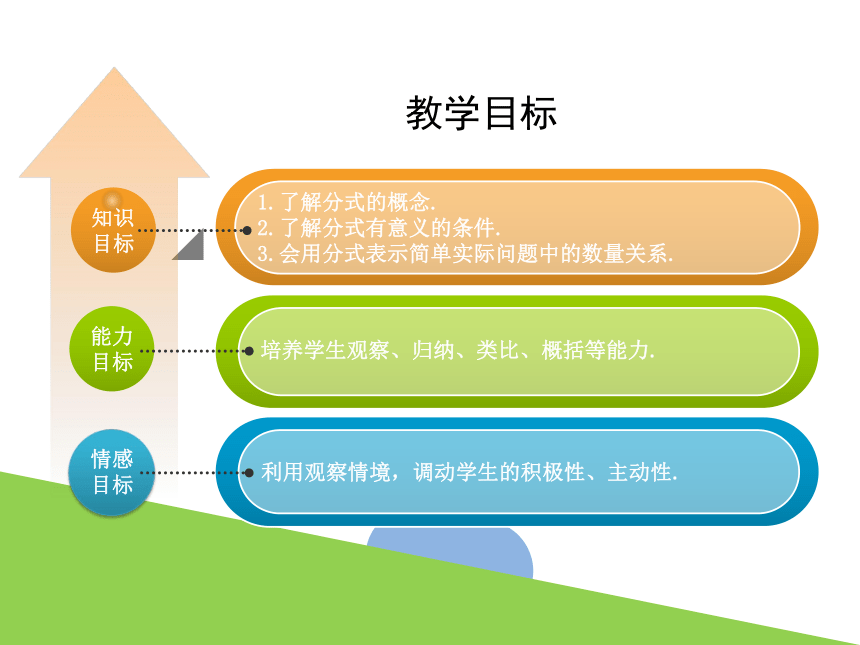
1.了解分式的概念.
2.了解分式有意义的条件.
3.会用分式表示简单实际问题中的数量关系.
教学目标
培养学生观察、归纳、类比、概括等能力.
利用观察情境,调动学生的积极性、主动性.
知识目标
能力目标
情感目标
新课引入
为了调查珍稀动物资源,动物专家在p平方千米的保护区内找到7只灰熊.你能用代数式表示该保护区平均每平方千米内有多少只灰熊吗?
讲解新知
3÷7=
这些代数式都比较两个整数相除,且除式中含有字母.像这样的代数式就叫做分式.
讲解新知
分式中字母的取值不能使分母为零.当分母的值为零时,分式就没有意义.
例题分析
例1 已知分式 .
(1) 当x取什么数时,分式有意义?
(2) 当x取什么数时,分式的值是零?
(3) 当x=1时,分式的值是多少?
解
(1)当分母等于零时,分式没有意义.
由3x-5=0,得x= .
所以当x取除 以外的任何实数时,分式 有意义.
甲﹑乙两人从一条公路的某处出发,同向而行.已知甲每时行a千米,乙每时行b千米,a>b.如果乙提前1时出发,那么甲追上乙需要多少时间?当a=6,b=5时,求甲追上乙所需要的时间?
解:根据题意,乙先行1时的路程是1×b(千米),甲比乙每小时多行(a-b)千米,所以甲追上乙所需的时间是
b÷(a-b)= (时)
例题分析
例2
答:甲追上乙需要 时.当a=6,b=5时,甲追上乙需5时.
当a=6,b=5时,甲追上乙所需的时间是
=
=5(时)
练一练
1.填空:
(1)当_______时,分式 有意义.
(2)当_______时,分式 有意义.
(3)当_______时,分式 的值是零.
练一练
2.甲、乙两人分别从A,B两地出发,相向而行.已知甲的速度为 千米/时,乙的速度为 千米/时,A,B两地相距20千米.若甲先出发1小时,问乙出发后多少时间与甲相遇?
拓展提高
(2)当m=30, n=10时,求船往返一次需要的时间.
(1)船从河边两地往返一次需要多少时间
河边两地相距50千米;船在静水中的速度是m千米/时,水流速度是n千米/时,那么:
由题意得,船的顺水速度是(m+n)千米/时,逆水速度(m-n)千米/时.
①则船往返一次需要的时间是: (时)
m+n m-n
50 50
+
②当m=30, n=10时,船往返一次需要的时间是:
m+n m-n
50 50
+
50 50
+
30+10 30-10
= =
15
4
(时)
答:船从河边两地往返一次需要 时,
m+n m-n
50 50
+
当m=30, n=10时,船往返一次需要
15
4
时.
解:
小结
(3)分式 的值为零时的条件:
(2)分式 有意义的条件.
(1)分式 的概念.
②B≠0
①A =0
再见
谢谢大家!
浙教版七(下)
第五章 分式
5.1 分式
1.了解分式的概念.
2.了解分式有意义的条件.
3.会用分式表示简单实际问题中的数量关系.
教学目标
培养学生观察、归纳、类比、概括等能力.
利用观察情境,调动学生的积极性、主动性.
知识目标
能力目标
情感目标
新课引入
为了调查珍稀动物资源,动物专家在p平方千米的保护区内找到7只灰熊.你能用代数式表示该保护区平均每平方千米内有多少只灰熊吗?
讲解新知
3÷7=
这些代数式都比较两个整数相除,且除式中含有字母.像这样的代数式就叫做分式.
讲解新知
分式中字母的取值不能使分母为零.当分母的值为零时,分式就没有意义.
例题分析
例1 已知分式 .
(1) 当x取什么数时,分式有意义?
(2) 当x取什么数时,分式的值是零?
(3) 当x=1时,分式的值是多少?
解
(1)当分母等于零时,分式没有意义.
由3x-5=0,得x= .
所以当x取除 以外的任何实数时,分式 有意义.
甲﹑乙两人从一条公路的某处出发,同向而行.已知甲每时行a千米,乙每时行b千米,a>b.如果乙提前1时出发,那么甲追上乙需要多少时间?当a=6,b=5时,求甲追上乙所需要的时间?
解:根据题意,乙先行1时的路程是1×b(千米),甲比乙每小时多行(a-b)千米,所以甲追上乙所需的时间是
b÷(a-b)= (时)
例题分析
例2
答:甲追上乙需要 时.当a=6,b=5时,甲追上乙需5时.
当a=6,b=5时,甲追上乙所需的时间是
=
=5(时)
练一练
1.填空:
(1)当_______时,分式 有意义.
(2)当_______时,分式 有意义.
(3)当_______时,分式 的值是零.
练一练
2.甲、乙两人分别从A,B两地出发,相向而行.已知甲的速度为 千米/时,乙的速度为 千米/时,A,B两地相距20千米.若甲先出发1小时,问乙出发后多少时间与甲相遇?
拓展提高
(2)当m=30, n=10时,求船往返一次需要的时间.
(1)船从河边两地往返一次需要多少时间
河边两地相距50千米;船在静水中的速度是m千米/时,水流速度是n千米/时,那么:
由题意得,船的顺水速度是(m+n)千米/时,逆水速度(m-n)千米/时.
①则船往返一次需要的时间是: (时)
m+n m-n
50 50
+
②当m=30, n=10时,船往返一次需要的时间是:
m+n m-n
50 50
+
50 50
+
30+10 30-10
= =
15
4
(时)
答:船从河边两地往返一次需要 时,
m+n m-n
50 50
+
当m=30, n=10时,船往返一次需要
15
4
时.
解:
小结
(3)分式 的值为零时的条件:
(2)分式 有意义的条件.
(1)分式 的概念.
②B≠0
①A =0
再见
谢谢大家!
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
