浙教版七年级数学每日一题71-75旋转中的平行存在性问题(含解析)
文档属性
| 名称 | 浙教版七年级数学每日一题71-75旋转中的平行存在性问题(含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-28 15:25:49 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
七年级每日一题71——旋转中的平行线存在性问题
班级 姓名 学号
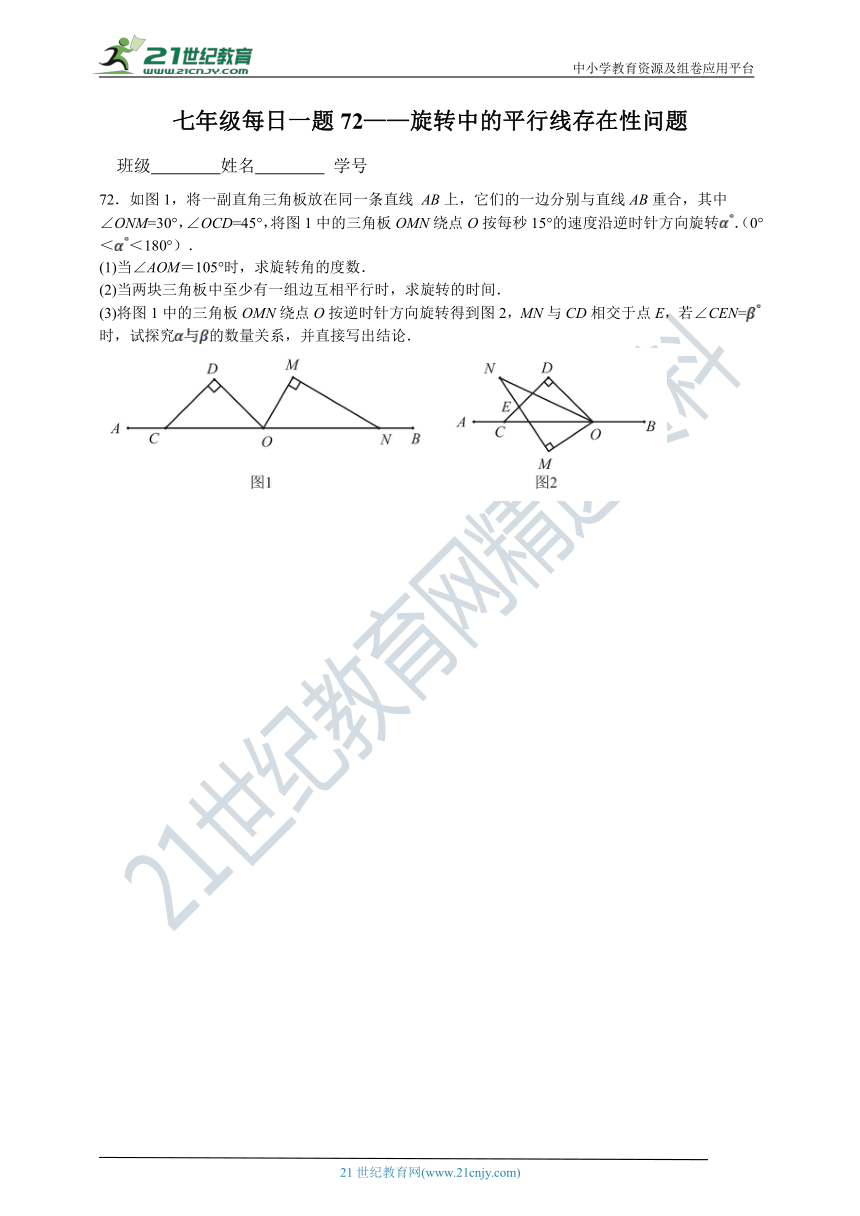
71.如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC=60°.将一把直角三角尺的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方,其中∠OMN=30°.
(1)将图1中的三角尺绕点O顺时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC,求∠CON的度数;
(2)将图1中的三角尺绕点O按每秒6°的速度绕点O沿顺时针方向旋转一周,OC也以每秒1°的速度绕点O顺时针方向旋转,当三角尺停止运动时,OC也停止运动.
①在旋转的过程中,问运动几秒时,边MN恰好与射线OC平行;
②将图1中的三角尺绕点O顺时针旋转至图3,使ON在∠AOC的内部,请探究∠AOM与∠NOC之间的数量关系(直接写出结果).
七年级每日一题72——旋转中的平行线存在性问题
班级 姓名 学号
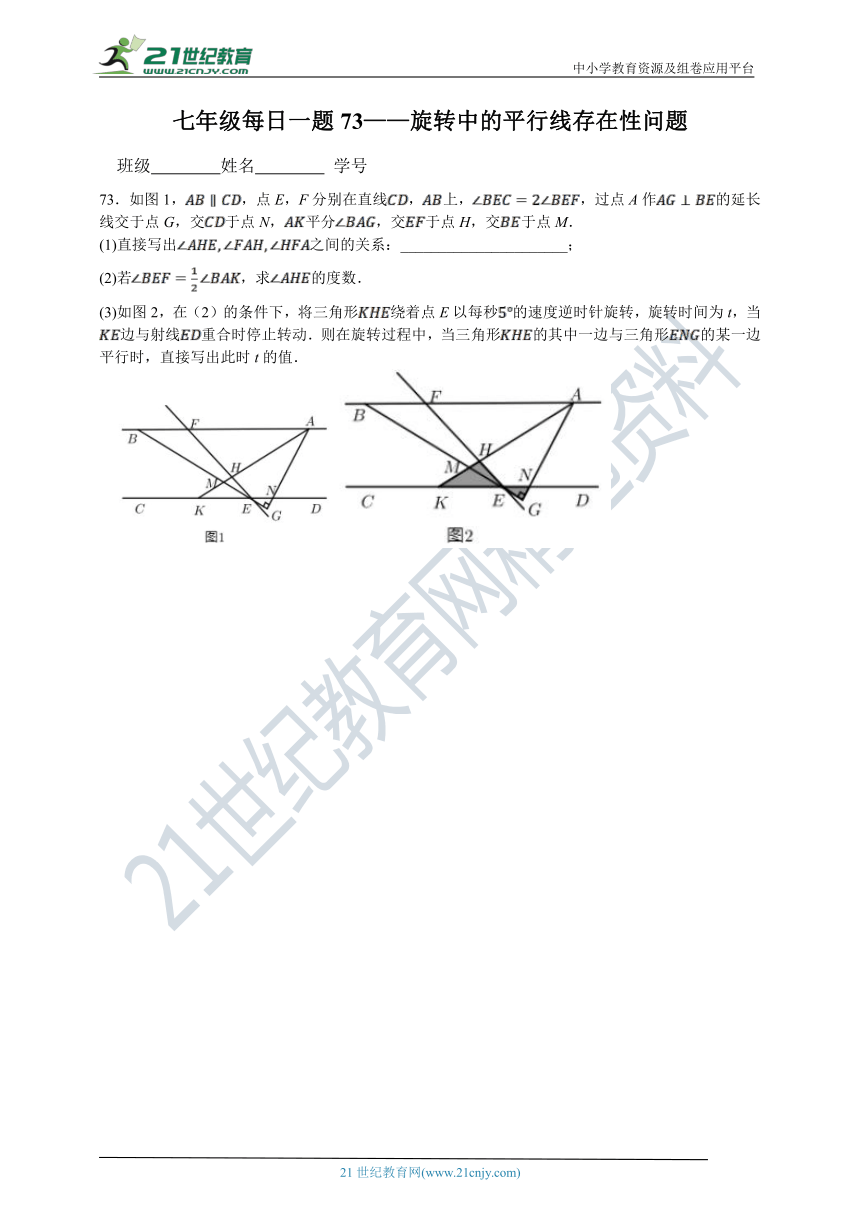
72.如图1,将一副直角三角板放在同一条直线 AB上,它们的一边分别与直线AB重合,其中∠ONM=30°,∠OCD=45°,将图1中的三角板OMN绕点O按每秒15°的速度沿逆时针方向旋转.(0°<<180°).
(1)当∠AOM=105°时,求旋转角的度数.
(2)当两块三角板中至少有一组边互相平行时,求旋转的时间.
(3)将图1中的三角板OMN绕点O按逆时针方向旋转得到图2,MN与CD相交于点E,若∠CEN=时,试探究的数量关系,并直接写出结论.
七年级每日一题73——旋转中的平行线存在性问题
班级 姓名 学号
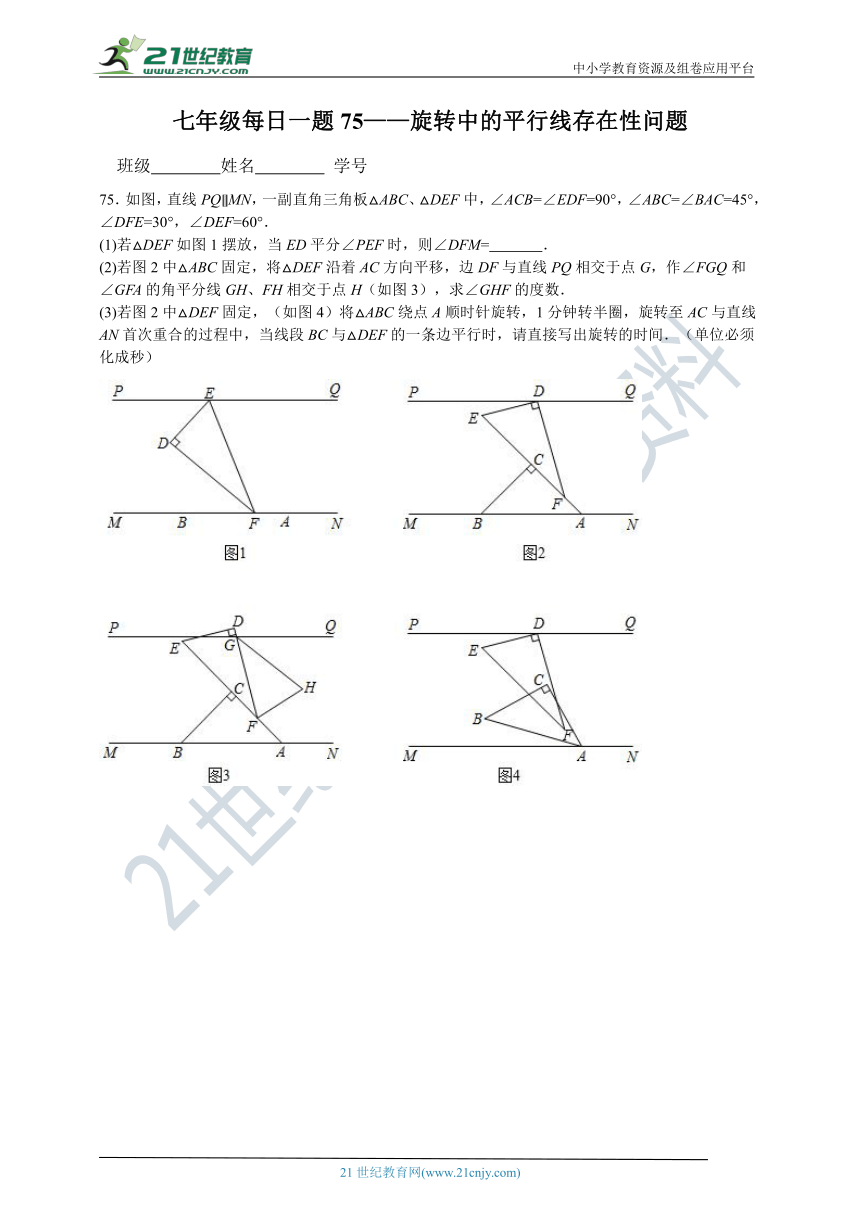
73.如图1,,点E,F分别在直线,上,,过点A作的延长线交于点G,交于点N,平分,交于点H,交于点M.
(1)直接写出之间的关系:______________________;
(2)若,求的度数.
(3)如图2,在(2)的条件下,将三角形绕着点E以每秒的速度逆时针旋转,旋转时间为t,当边与射线重合时停止转动.则在旋转过程中,当三角形的其中一边与三角形的某一边平行时,直接写出此时t的值.
七年级每日一题74——旋转中的平行线存在性问题
班级 姓名 学号
74.如图1,点O为直线上一点,过点O作射线,使,将一把直角三角尺的直角顶点放在点O处,一边在射线上,另一边在直线的下方,其中.
(1)将图1中的三角尺绕点O顺时针旋转至图2,使一边在的内部,且恰好平分,求的度数;
(2)将图1中的三角尺绕点O顺时针旋转至图3,使在的内部,请探究与之间的数量关系,并说明理由.
(3)将图1中三角尺绕点O按每秒的速度沿顺时针方向旋转一周,旋转过程中,在第_____秒时,边恰好与射线平行;在第_______秒时,直线恰好平分锐角.
七年级每日一题75——旋转中的平行线存在性问题
班级 姓名 学号
75.如图,直线PQMN,一副直角三角板△ABC、△DEF中,∠ACB=∠EDF=90°,∠ABC=∠BAC=45°,∠DFE=30°,∠DEF=60°.
(1)若△DEF如图1摆放,当ED平分∠PEF时,则∠DFM= .
(2)若图2中△ABC固定,将△DEF沿着AC方向平移,边DF与直线PQ相交于点G,作∠FGQ和∠GFA的角平分线GH、FH相交于点H(如图3),求∠GHF的度数.
(3)若图2中△DEF固定,(如图4)将△ABC绕点A顺时针旋转,1分钟转半圈,旋转至AC与直线AN首次重合的过程中,当线段BC与△DEF的一条边平行时,请直接写出旋转的时间.(单位必须化成秒)
七年级每日一题71答案
71.(1)解:∵∠AOC=60°,
∴∠BOC=120°,
又∵OM平分∠BOC,
∴∠COM=∠BOC=60°,
∴∠CON=∠COM+90°=150°;
(2)解:①∵∠OMN=30°,
∴∠COM=30°或∠CON=30°时是可以满足MNOC,
即(90°+60°-60°)÷(6°-1°)=18s,
(180°+60°+30°)÷(6°-1°)=54s,
故答案为:18s或54s.
②设运动的时间为t,则
∠AOM=180°-6t=6(30°-t),
∠NOC=60°+t-(90°-180°+6t)=5(30°-t),
故∠AOM与∠NOC之间的数量关系为:5∠AOM=6∠NOC.
七年级每日一题72答案
72.(1)解:如图所示,∠AOM=105°时,∠MOB=180°-105°=75°,
∵∠MON=60°,∴∠BON=75°-60°=15°,即旋转角为15°;
(2)如图,
当MNOC时,∠COM=∠M=90°,
∠BON=180°﹣∠AOM﹣∠MON=30°,此时t=30÷15=2s;
当ONCD时,∠BON=∠OCD=45°, 此时t=45÷15=3s;
当MNCD时,
∴∠D=∠OMN=90°,∴此时点M在OD上,∠BON=180°﹣∠AOM﹣∠MON=75°,
此时t=75÷15=5s;
如图,设CD与MN相交于点E,
当MNOD时,∠DEM=∠D=90°,
∴∠DOM=360°﹣∠D﹣∠DEM﹣∠M =90°,∴四边形DEMO为矩形,∴MOCD,
∵∠DON=∠DOM﹣∠NOM =90°﹣60°=30°,
∴∠AON=∠COD﹣∠DON =45°﹣30°=15°,
∴∠BON=180°﹣∠AON=165°,此时t=165÷15=11s;
∴当两块三角板中至少有一组边互相平行时,旋转的时间为2s或3s或5s或11s.
(3)由图可得,∠BON为旋转角,即∠BON=,
∵∠COD=45°,∴∠DOB=135°,∴∠DON=﹣135°,
∵∠MON=60°,∴∠DOM=60°+﹣135°=﹣75°,
∵∠DEM+∠D +∠DOM +∠M=360°,∠DEM=∠CEN=,
∴+90°+90°+﹣75°=360°,∴+=255.
七年级每日一题73答案
73.(1)解:∵是的外角,
∴;
故答案为:.
(2)解:设,
∵,,
∴,
∵平分,
∴,
∵为的外角,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∴
∴;
(3)解:由(2)可得,,
,,
,
∵,
∴,
①当时,
解得:;
②当时,
,
解得:;
③当时
,
解得:,
④当时,
,
解得:;
⑤当时,
解得:;
综上所述,t的值为6或12或21或24或30.
七年级每日一题74答案
74.解:(1)∵∠AOC=120°,∴∠BOC=60°,
又∵OM平分∠AOC,∴∠COM=∠BOC=60°,∴∠CON=∠COM+90°=150°;
(2)∵∠MON=90°,∠BOC=60°,∴∠BON=90°-∠BOM,
∠BON=60°-∠CON,∴90°-∠BOM=60°-∠CON,∴∠BOM-∠CON=30°,
故∠BOM与∠CON之间的数量关系为:∠BOM-∠CON=30°.
(3)∵∠OMN=30°,∴∠N=90°-30°=60°,
∵∠BOC=60°,∴当ON在直线AB上时,MN∥OC,
如图,则旋转角为90°或270°,
∵每秒顺时针旋转10°,
∴时间为9秒或27秒;
当直线ON恰好平分锐角∠BOC时,
则旋转角为90°-30°=60°或90°+150°=240°,
∵每秒顺时针旋转10°,
∴时间为6秒或24秒.
七年级每日一题75答案
75.(1)解:∵平分,,∴,
∵PQMN,,∴,
,∴.故答案为:30°
(2)解:如图3,分别过点,作FLMN,HRPQ,
∴,,
∵FLMN,HRPQ,PQMN,∴FLPQHR,,
∴,,
∵,∴,
∵和的角平分线、相交于点,
∴,
∴,
∴,
∴∠QGF=180°-∠GFL=75°,∴,
∴;
(3)解:设旋转时间为秒,由题意旋转速度为1分钟转半圈,即每秒转,
分三种情况:当BCDE时,如图5,
此时ACDF,,,解得:;
②当BCEF时,如图6,
∵BCEF,,,
,解得:;
③当BCDF时,如图7,
延长交于,延长交于,
,,
,,
,,
解得:,
综上所述,绕点顺时针旋转的时间为10s或30s或40s时,线段与的一条边平行.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
七年级每日一题71——旋转中的平行线存在性问题
班级 姓名 学号
71.如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC=60°.将一把直角三角尺的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方,其中∠OMN=30°.
(1)将图1中的三角尺绕点O顺时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC,求∠CON的度数;
(2)将图1中的三角尺绕点O按每秒6°的速度绕点O沿顺时针方向旋转一周,OC也以每秒1°的速度绕点O顺时针方向旋转,当三角尺停止运动时,OC也停止运动.
①在旋转的过程中,问运动几秒时,边MN恰好与射线OC平行;
②将图1中的三角尺绕点O顺时针旋转至图3,使ON在∠AOC的内部,请探究∠AOM与∠NOC之间的数量关系(直接写出结果).
七年级每日一题72——旋转中的平行线存在性问题
班级 姓名 学号
72.如图1,将一副直角三角板放在同一条直线 AB上,它们的一边分别与直线AB重合,其中∠ONM=30°,∠OCD=45°,将图1中的三角板OMN绕点O按每秒15°的速度沿逆时针方向旋转.(0°<<180°).
(1)当∠AOM=105°时,求旋转角的度数.
(2)当两块三角板中至少有一组边互相平行时,求旋转的时间.
(3)将图1中的三角板OMN绕点O按逆时针方向旋转得到图2,MN与CD相交于点E,若∠CEN=时,试探究的数量关系,并直接写出结论.
七年级每日一题73——旋转中的平行线存在性问题
班级 姓名 学号
73.如图1,,点E,F分别在直线,上,,过点A作的延长线交于点G,交于点N,平分,交于点H,交于点M.
(1)直接写出之间的关系:______________________;
(2)若,求的度数.
(3)如图2,在(2)的条件下,将三角形绕着点E以每秒的速度逆时针旋转,旋转时间为t,当边与射线重合时停止转动.则在旋转过程中,当三角形的其中一边与三角形的某一边平行时,直接写出此时t的值.
七年级每日一题74——旋转中的平行线存在性问题
班级 姓名 学号
74.如图1,点O为直线上一点,过点O作射线,使,将一把直角三角尺的直角顶点放在点O处,一边在射线上,另一边在直线的下方,其中.
(1)将图1中的三角尺绕点O顺时针旋转至图2,使一边在的内部,且恰好平分,求的度数;
(2)将图1中的三角尺绕点O顺时针旋转至图3,使在的内部,请探究与之间的数量关系,并说明理由.
(3)将图1中三角尺绕点O按每秒的速度沿顺时针方向旋转一周,旋转过程中,在第_____秒时,边恰好与射线平行;在第_______秒时,直线恰好平分锐角.
七年级每日一题75——旋转中的平行线存在性问题
班级 姓名 学号
75.如图,直线PQMN,一副直角三角板△ABC、△DEF中,∠ACB=∠EDF=90°,∠ABC=∠BAC=45°,∠DFE=30°,∠DEF=60°.
(1)若△DEF如图1摆放,当ED平分∠PEF时,则∠DFM= .
(2)若图2中△ABC固定,将△DEF沿着AC方向平移,边DF与直线PQ相交于点G,作∠FGQ和∠GFA的角平分线GH、FH相交于点H(如图3),求∠GHF的度数.
(3)若图2中△DEF固定,(如图4)将△ABC绕点A顺时针旋转,1分钟转半圈,旋转至AC与直线AN首次重合的过程中,当线段BC与△DEF的一条边平行时,请直接写出旋转的时间.(单位必须化成秒)
七年级每日一题71答案
71.(1)解:∵∠AOC=60°,
∴∠BOC=120°,
又∵OM平分∠BOC,
∴∠COM=∠BOC=60°,
∴∠CON=∠COM+90°=150°;
(2)解:①∵∠OMN=30°,
∴∠COM=30°或∠CON=30°时是可以满足MNOC,
即(90°+60°-60°)÷(6°-1°)=18s,
(180°+60°+30°)÷(6°-1°)=54s,
故答案为:18s或54s.
②设运动的时间为t,则
∠AOM=180°-6t=6(30°-t),
∠NOC=60°+t-(90°-180°+6t)=5(30°-t),
故∠AOM与∠NOC之间的数量关系为:5∠AOM=6∠NOC.
七年级每日一题72答案
72.(1)解:如图所示,∠AOM=105°时,∠MOB=180°-105°=75°,
∵∠MON=60°,∴∠BON=75°-60°=15°,即旋转角为15°;
(2)如图,
当MNOC时,∠COM=∠M=90°,
∠BON=180°﹣∠AOM﹣∠MON=30°,此时t=30÷15=2s;
当ONCD时,∠BON=∠OCD=45°, 此时t=45÷15=3s;
当MNCD时,
∴∠D=∠OMN=90°,∴此时点M在OD上,∠BON=180°﹣∠AOM﹣∠MON=75°,
此时t=75÷15=5s;
如图,设CD与MN相交于点E,
当MNOD时,∠DEM=∠D=90°,
∴∠DOM=360°﹣∠D﹣∠DEM﹣∠M =90°,∴四边形DEMO为矩形,∴MOCD,
∵∠DON=∠DOM﹣∠NOM =90°﹣60°=30°,
∴∠AON=∠COD﹣∠DON =45°﹣30°=15°,
∴∠BON=180°﹣∠AON=165°,此时t=165÷15=11s;
∴当两块三角板中至少有一组边互相平行时,旋转的时间为2s或3s或5s或11s.
(3)由图可得,∠BON为旋转角,即∠BON=,
∵∠COD=45°,∴∠DOB=135°,∴∠DON=﹣135°,
∵∠MON=60°,∴∠DOM=60°+﹣135°=﹣75°,
∵∠DEM+∠D +∠DOM +∠M=360°,∠DEM=∠CEN=,
∴+90°+90°+﹣75°=360°,∴+=255.
七年级每日一题73答案
73.(1)解:∵是的外角,
∴;
故答案为:.
(2)解:设,
∵,,
∴,
∵平分,
∴,
∵为的外角,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∴
∴;
(3)解:由(2)可得,,
,,
,
∵,
∴,
①当时,
解得:;
②当时,
,
解得:;
③当时
,
解得:,
④当时,
,
解得:;
⑤当时,
解得:;
综上所述,t的值为6或12或21或24或30.
七年级每日一题74答案
74.解:(1)∵∠AOC=120°,∴∠BOC=60°,
又∵OM平分∠AOC,∴∠COM=∠BOC=60°,∴∠CON=∠COM+90°=150°;
(2)∵∠MON=90°,∠BOC=60°,∴∠BON=90°-∠BOM,
∠BON=60°-∠CON,∴90°-∠BOM=60°-∠CON,∴∠BOM-∠CON=30°,
故∠BOM与∠CON之间的数量关系为:∠BOM-∠CON=30°.
(3)∵∠OMN=30°,∴∠N=90°-30°=60°,
∵∠BOC=60°,∴当ON在直线AB上时,MN∥OC,
如图,则旋转角为90°或270°,
∵每秒顺时针旋转10°,
∴时间为9秒或27秒;
当直线ON恰好平分锐角∠BOC时,
则旋转角为90°-30°=60°或90°+150°=240°,
∵每秒顺时针旋转10°,
∴时间为6秒或24秒.
七年级每日一题75答案
75.(1)解:∵平分,,∴,
∵PQMN,,∴,
,∴.故答案为:30°
(2)解:如图3,分别过点,作FLMN,HRPQ,
∴,,
∵FLMN,HRPQ,PQMN,∴FLPQHR,,
∴,,
∵,∴,
∵和的角平分线、相交于点,
∴,
∴,
∴,
∴∠QGF=180°-∠GFL=75°,∴,
∴;
(3)解:设旋转时间为秒,由题意旋转速度为1分钟转半圈,即每秒转,
分三种情况:当BCDE时,如图5,
此时ACDF,,,解得:;
②当BCEF时,如图6,
∵BCEF,,,
,解得:;
③当BCDF时,如图7,
延长交于,延长交于,
,,
,,
,,
解得:,
综上所述,绕点顺时针旋转的时间为10s或30s或40s时,线段与的一条边平行.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
