浙教版七年级数学每日一题76-80三角板的旋转探究问题(含解析)
文档属性
| 名称 | 浙教版七年级数学每日一题76-80三角板的旋转探究问题(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-28 15:28:57 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
七年级每日一题76——三角板的旋转探究问题
班级 姓名 学号
76.如图1,直线上有一点,过点在直线上方作射线,将一直角三角板的直角顶点放在处,,,一条直角边在射线上,另一边在直线上方,将直角三角板绕着点按每秒10°的速度逆时针旋转一周停止,设旋转时间为t秒,且.
(1)若射线的位置保持不变,则当旋转时间______秒时,边所在直线与平行;
(2)如图2,在旋转的过程中,若射线的位置保持不变,是否存在某个时刻,使得射线,与中的某一条射线是另两条射线所成夹角的平分线?若存在,求出所有满足题意的的取值,若不存在,请说明理由;
七年级每日一题77——三角板的旋转探究问题
班级 姓名 学号
77.如图1,将三角板与三角板摆放在一起,其中,,,固定三角板,将三角板绕点A按顺时针方向旋转,当点E落在射线的反向延长线上时,即停止旋转.
(1)如图2,当边落在内,
①与之间存在怎样的数量关系?试说明理由;
②过点A作射线,,若,,求的度数;
(2) 设的旋转速度为3°/秒,旋转时间为t,若它的一边与的某一边平行(不含重合情况),试写出所有符合条件的t的值.
七年级每日一题78——三角板的旋转探究问题
班级 姓名 学号
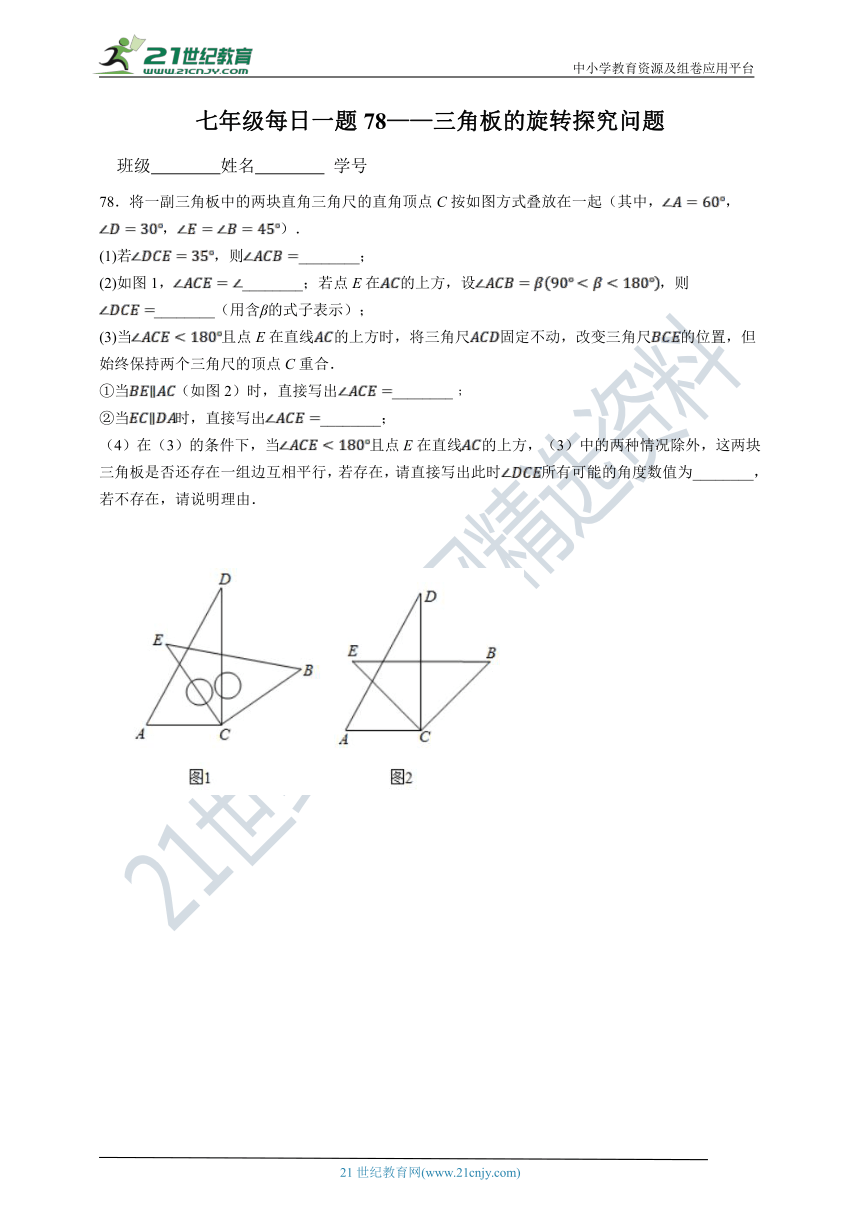
78.将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中,,,).
(1)若,则________;
(2)如图1,________;若点E在的上方,设,则________(用含β的式子表示);
(3)当且点E在直线的上方时,将三角尺固定不动,改变三角尺的位置,但始终保持两个三角尺的顶点C重合.
①当(如图2)时,直接写出________﹔
②当时,直接写出________;
(4)在(3)的条件下,当且点E在直线的上方,(3)中的两种情况除外,这两块三角板是否还存在一组边互相平行,若存在,请直接写出此时所有可能的角度数值为________,若不存在,请说明理由.
七年级每日一题79——三角板的旋转探究问题
班级 姓名 学号
79.如图,直线,一副三角尺(,,,)按如图①放置,其中点在直线上,点,均在直线上,且平分.
(1)求的度数.
(2)如图②,若将三角形绕点以每秒2度的速度按逆时针方向旋转(,的对应点分别为,),设旋转时间为.
①在旋转过程中,当时,求的值.
②若在三角形绕点旋转的同时,三角形绕点以每秒1度的速度按顺时针方向旋转(,的对应点为,),请直接写出当时的值.
七年级每日一题80——三角板的旋转探究问题
班级 姓名 学号
80.综合与实践
问题情境:
在数学实践课上,给出两个大小形状完全相同的含有,的直角三角板如图1放置,在直线上,且三角板和三角板均可以点P为顶点运动.
操作探究:
(1)如图2,若三角板保持不动,三角板绕点P逆时针旋转一定角度,平分平分,求;
(2)如图3,在图1基础上,若三角板开始绕点P以每秒的速度逆时针旋转,同时三角板绕点P以每秒的速度逆时针旋转,当转到与重合时,两三角板都停止转动.在旋转过程中,当三条射线中的其中一条射线平分另两条射线的夹角时,请求出旋转的时间;
拓广探究:
(3)如图4,作三角板关于直线的对称图形.三角板保持不动,三角板绕点P逆时针旋转,当时,请直接写出旋转角的度数.
七年级每日一题76答案
76.(1)解:如图3, ,,,
∵,
∴,
∴,
∴,;
如图4,,,,,
∴,
∵,
∴,
∴,
∵,
∴,
解得:;
所以当旋转时间为7或秒,边所在直线与平行;
(2)当平分时,如图5,,
∵平分,
∴,
∴,则;
当平分时,如图6,
∵平分,
∴,即,则;
当平分时,如图7,
∵平分,
∴,即,则;
综上所述,满足题意的t的取值为2或8或32.
七年级每日一题77答案
77.(1)解:①(或);
理由如下:,,
两式相减得:,
② ∵, ∴,
∵,∴,
∴,
∴
;
(2)如图1,当时,
∴,,∴;
图1 图2 图3 图4
如图2,当时,
∴,则,
此时,∴;
如图3,当时,
∴,,
∴,
∴,∴;
如图,当时,
∴,即,,共线,
∴,∴; 图5
如图5,当时,
∴,∴,∴.
七年级每日一题78答案
78(1)∵,
∴
(2)∵,,
∴ ∴
∴,
(3)①当时,
∵, ∴,
②当时,如图,
∵,∴,
∴,
(4)①当时,
∵,∴,;
②当时,∴;
③当时,过点C作,
∵,
∴,
∴,,
∴;
综上所述:为或或.
七年级每日一题79答案
79(1)解:如图①中,
∵∠ACB=30°,∴∠ACN=180°﹣∠ACB=150°,
∵CE平分∠ACN,∴∠ECN=∠ACN=75°,
∵PQMN,∴∠QEC+∠ECN=180°,
∴∠QEC=180°﹣75°=105°,
∴∠DEQ=∠QEC﹣∠CED=105°﹣45°=60°.
(2)解:①如图②中,
∵BGCD,∴∠GBC=∠DCN,
∵∠DCN=∠ECN﹣∠ECD=75°﹣45°=30°,∴∠GBC=30°,
∴2t=30,∴t=15s.
∴在旋转过程中,若边BGCD,t的值为15s.
②如图③中,当BGHK时,延长KH交MN于R.
∵BGKR,∴∠GBN=∠KRN,
过点K作KTPQ,则PQKTMN,
∴∠QEK=∠EKT,∠KRN=∠HKT,
∴∠QEK=60°+t,∠K=∠QEK+∠KRN,
∴∠KRN=90°﹣(60°+t)=30°﹣t,∴2t=30°﹣t,∴t=10s.
如图③﹣1中,当BGHK时,延长HK交MN于R.
∵BGKR,∴∠GBN+∠KRM=180°,
同理可得∠QEK=60°+t,∠EKR=∠PEK+∠KRM,
∴∠KRM=90°﹣(180°﹣60°﹣t)=t﹣30°,
∴2t+t﹣30°=180°,∴t=70s.
综上所述,满足条件的t的值为10s或70s.
七年级每日一题80答案
80.(1)∵平分∠∴设∠
则∠∠
∴ ∴
∴∠
(2)设t秒时,其中一条射线平分另两条射线的夹角,
∵当PA转到与PM重合时,两三角板都停止转动,
∴秒,
分三种情况讨论:
①当PD平分∠BPC时,根据题意可列方程,
解得,,符合题意;
②当PC平分∠BPD时,根据题意可列方程,
解得,,符合题意;
③当PB平分∠CPD时,根据题意可列方程,
解得, ,不符合题意舍去,
所以,旋转时间为15秒或秒时,三条射线中的其中一条射线平分另两条射线的夹角;
(3)①如图①,
∵与关于PB对称,
∴
若,则
∴
∴
∴旋转角度数为:;
②如图②,
若,则
∴
∴旋转角度数为:;
综上,当时,旋转角的度数为30°或210°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
七年级每日一题76——三角板的旋转探究问题
班级 姓名 学号
76.如图1,直线上有一点,过点在直线上方作射线,将一直角三角板的直角顶点放在处,,,一条直角边在射线上,另一边在直线上方,将直角三角板绕着点按每秒10°的速度逆时针旋转一周停止,设旋转时间为t秒,且.
(1)若射线的位置保持不变,则当旋转时间______秒时,边所在直线与平行;
(2)如图2,在旋转的过程中,若射线的位置保持不变,是否存在某个时刻,使得射线,与中的某一条射线是另两条射线所成夹角的平分线?若存在,求出所有满足题意的的取值,若不存在,请说明理由;
七年级每日一题77——三角板的旋转探究问题
班级 姓名 学号
77.如图1,将三角板与三角板摆放在一起,其中,,,固定三角板,将三角板绕点A按顺时针方向旋转,当点E落在射线的反向延长线上时,即停止旋转.
(1)如图2,当边落在内,
①与之间存在怎样的数量关系?试说明理由;
②过点A作射线,,若,,求的度数;
(2) 设的旋转速度为3°/秒,旋转时间为t,若它的一边与的某一边平行(不含重合情况),试写出所有符合条件的t的值.
七年级每日一题78——三角板的旋转探究问题
班级 姓名 学号
78.将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中,,,).
(1)若,则________;
(2)如图1,________;若点E在的上方,设,则________(用含β的式子表示);
(3)当且点E在直线的上方时,将三角尺固定不动,改变三角尺的位置,但始终保持两个三角尺的顶点C重合.
①当(如图2)时,直接写出________﹔
②当时,直接写出________;
(4)在(3)的条件下,当且点E在直线的上方,(3)中的两种情况除外,这两块三角板是否还存在一组边互相平行,若存在,请直接写出此时所有可能的角度数值为________,若不存在,请说明理由.
七年级每日一题79——三角板的旋转探究问题
班级 姓名 学号
79.如图,直线,一副三角尺(,,,)按如图①放置,其中点在直线上,点,均在直线上,且平分.
(1)求的度数.
(2)如图②,若将三角形绕点以每秒2度的速度按逆时针方向旋转(,的对应点分别为,),设旋转时间为.
①在旋转过程中,当时,求的值.
②若在三角形绕点旋转的同时,三角形绕点以每秒1度的速度按顺时针方向旋转(,的对应点为,),请直接写出当时的值.
七年级每日一题80——三角板的旋转探究问题
班级 姓名 学号
80.综合与实践
问题情境:
在数学实践课上,给出两个大小形状完全相同的含有,的直角三角板如图1放置,在直线上,且三角板和三角板均可以点P为顶点运动.
操作探究:
(1)如图2,若三角板保持不动,三角板绕点P逆时针旋转一定角度,平分平分,求;
(2)如图3,在图1基础上,若三角板开始绕点P以每秒的速度逆时针旋转,同时三角板绕点P以每秒的速度逆时针旋转,当转到与重合时,两三角板都停止转动.在旋转过程中,当三条射线中的其中一条射线平分另两条射线的夹角时,请求出旋转的时间;
拓广探究:
(3)如图4,作三角板关于直线的对称图形.三角板保持不动,三角板绕点P逆时针旋转,当时,请直接写出旋转角的度数.
七年级每日一题76答案
76.(1)解:如图3, ,,,
∵,
∴,
∴,
∴,;
如图4,,,,,
∴,
∵,
∴,
∴,
∵,
∴,
解得:;
所以当旋转时间为7或秒,边所在直线与平行;
(2)当平分时,如图5,,
∵平分,
∴,
∴,则;
当平分时,如图6,
∵平分,
∴,即,则;
当平分时,如图7,
∵平分,
∴,即,则;
综上所述,满足题意的t的取值为2或8或32.
七年级每日一题77答案
77.(1)解:①(或);
理由如下:,,
两式相减得:,
② ∵, ∴,
∵,∴,
∴,
∴
;
(2)如图1,当时,
∴,,∴;
图1 图2 图3 图4
如图2,当时,
∴,则,
此时,∴;
如图3,当时,
∴,,
∴,
∴,∴;
如图,当时,
∴,即,,共线,
∴,∴; 图5
如图5,当时,
∴,∴,∴.
七年级每日一题78答案
78(1)∵,
∴
(2)∵,,
∴ ∴
∴,
(3)①当时,
∵, ∴,
②当时,如图,
∵,∴,
∴,
(4)①当时,
∵,∴,;
②当时,∴;
③当时,过点C作,
∵,
∴,
∴,,
∴;
综上所述:为或或.
七年级每日一题79答案
79(1)解:如图①中,
∵∠ACB=30°,∴∠ACN=180°﹣∠ACB=150°,
∵CE平分∠ACN,∴∠ECN=∠ACN=75°,
∵PQMN,∴∠QEC+∠ECN=180°,
∴∠QEC=180°﹣75°=105°,
∴∠DEQ=∠QEC﹣∠CED=105°﹣45°=60°.
(2)解:①如图②中,
∵BGCD,∴∠GBC=∠DCN,
∵∠DCN=∠ECN﹣∠ECD=75°﹣45°=30°,∴∠GBC=30°,
∴2t=30,∴t=15s.
∴在旋转过程中,若边BGCD,t的值为15s.
②如图③中,当BGHK时,延长KH交MN于R.
∵BGKR,∴∠GBN=∠KRN,
过点K作KTPQ,则PQKTMN,
∴∠QEK=∠EKT,∠KRN=∠HKT,
∴∠QEK=60°+t,∠K=∠QEK+∠KRN,
∴∠KRN=90°﹣(60°+t)=30°﹣t,∴2t=30°﹣t,∴t=10s.
如图③﹣1中,当BGHK时,延长HK交MN于R.
∵BGKR,∴∠GBN+∠KRM=180°,
同理可得∠QEK=60°+t,∠EKR=∠PEK+∠KRM,
∴∠KRM=90°﹣(180°﹣60°﹣t)=t﹣30°,
∴2t+t﹣30°=180°,∴t=70s.
综上所述,满足条件的t的值为10s或70s.
七年级每日一题80答案
80.(1)∵平分∠∴设∠
则∠∠
∴ ∴
∴∠
(2)设t秒时,其中一条射线平分另两条射线的夹角,
∵当PA转到与PM重合时,两三角板都停止转动,
∴秒,
分三种情况讨论:
①当PD平分∠BPC时,根据题意可列方程,
解得,,符合题意;
②当PC平分∠BPD时,根据题意可列方程,
解得,,符合题意;
③当PB平分∠CPD时,根据题意可列方程,
解得, ,不符合题意舍去,
所以,旋转时间为15秒或秒时,三条射线中的其中一条射线平分另两条射线的夹角;
(3)①如图①,
∵与关于PB对称,
∴
若,则
∴
∴
∴旋转角度数为:;
②如图②,
若,则
∴
∴旋转角度数为:;
综上,当时,旋转角的度数为30°或210°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
