浙教版七年级数学每日一题106-110平行线问题的综合探究(含解析)
文档属性
| 名称 | 浙教版七年级数学每日一题106-110平行线问题的综合探究(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-28 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
七年级每日一题106——平行线问题的综合探究
班级 姓名 学号
106.若两个角的一组边互相平行,另一组边互相垂直,则称这两个角互为“旁系衍生角”.
(1)如图1,,于点,则与互为“旁系衍生角”.当时,求的度数;
(2)当为锐角时,若与两个角互为“旁系衍生角”,则这两个角的数量关系为________________;
(3)如图2,若,,垂足为点A,,分别平分和,且相交于点,求的度数.
七年级每日一题107——平行线问题的综合探究
班级 姓名 学号
107.如图1,已知,,点E在CD上,点G,F在AB上,点H在AB,CD之间,连接FE,EH,HG,.
(1)求证:;
(2)如图2,FK平分∠AFE交CD于点K,,GM平分∠HGB,若,求∠GHE的度数;
(3)如图3,FK平分∠AFE交CD于点K,,GM平分∠HGB,EM平分∠HED,GM,EM交于点M,若,,求的值.(请直接写出答案)
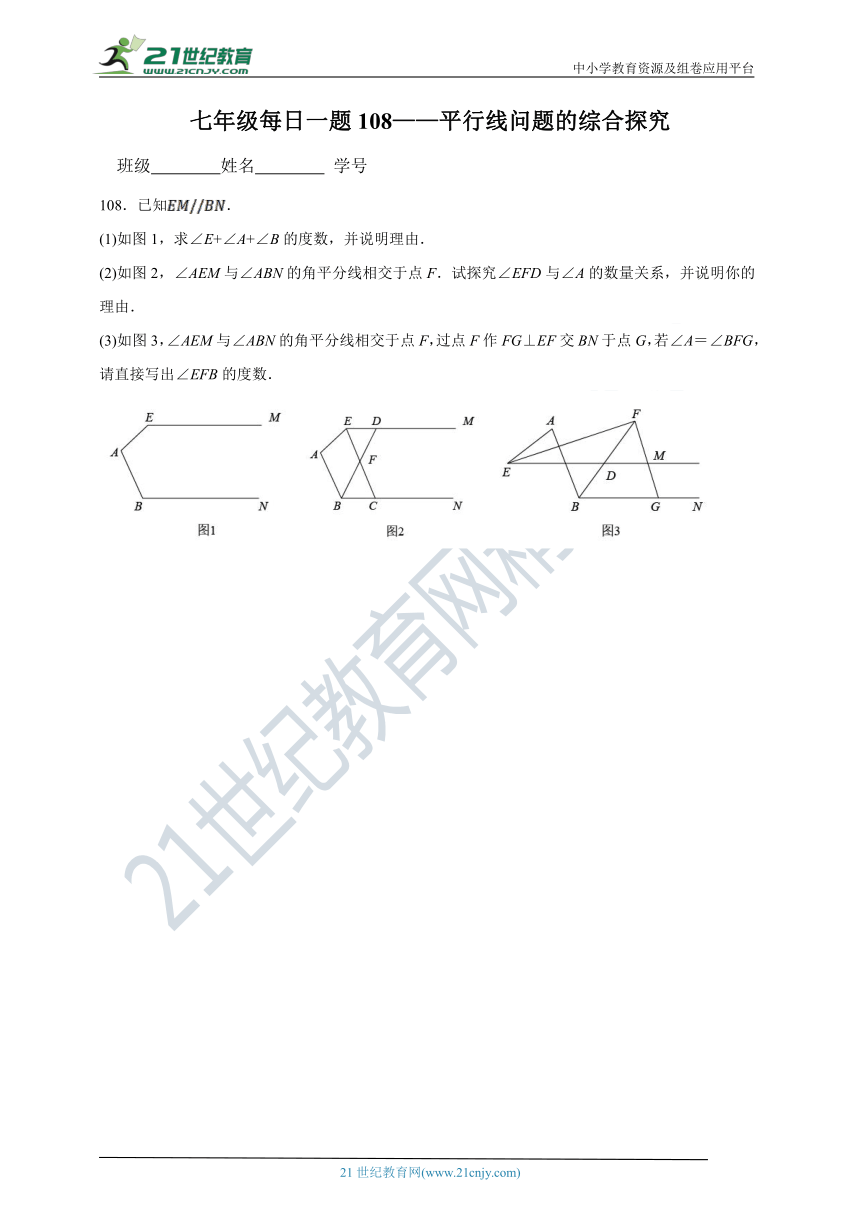
七年级每日一题108——平行线问题的综合探究
班级 姓名 学号
108.已知.
(1)如图1,求∠E+∠A+∠B的度数,并说明理由.
(2)如图2,∠AEM与∠ABN的角平分线相交于点F.试探究∠EFD与∠A的数量关系,并说明你的理由.
(3)如图3,∠AEM与∠ABN的角平分线相交于点F,过点F作FG⊥EF交BN于点G,若∠A=∠BFG,请直接写出∠EFB的度数.
七年级每日一题109——平行线问题的综合探究
班级 姓名 学号
109.如图1,直线,另一直线分别交AB、CD于M、N,将射线MA绕点M以每秒2°的速度逆时针旋转到,同时射线NC绕点N以每秒3°的速度顺时针旋转到,旋转的时间为t()秒.
(1)如图2,当秒时,射线与相交于点P,求的度数;
(2)如图3,当射线与平行时,求t的值;
(3)当射线与互相垂直时,求t的值.
七年级每日一题110——平行线问题的综合探究
班级 姓名 学号
110.如图甲所示,已知点在直线上,点,在直线上,且,平分.
(1)判断直线与直线是否平行,并说明理由.
(2)如图乙所示,是上点右侧一动点,的平分线交的延长线于点,设,
①若,,求的度数.
②点在运动过程中,请直接写出和的数量关系.
七年级每日一题106——答案
解:∵,
∴∠ADG=90°,
∵,
∴,
∵,
∴.
(2)
或.
(3)
解:∵,
∴,
∵BA⊥AD,
∴∠BAD=90°,
∴,
∴,
∵DE平分∠ADF,
∴,
∵AE平分∠BAC,
∴,
∴,
∴
七年级每日一题107——答案
(1)解:∵,∴.
∵,∴,
∴;
(2)解:如图,过点H作.
∴.
∵,
故可设,则.
∵,
∴,,.
∵FK平分∠AFE,GM平分∠HGB,
∴,,
∴,.
由(1)可知,∴,∴,
解得:.
∴,.
∵,∴,
∴;
(3)解:如图,过点M作.
由题意可设,则.
∵,FK平分∠AFE
∴,.
∵,∴.
∵EM平分∠HED,∴.
∵, ∴,
∴.
∵GM平分∠HGB, ∴,,
∴.
∵, ∴.
∴,即.
由(1)可知,∴,∴.
即,解得:,
∴.
七年级每日一题108——答案
【详解】(1)解:过A作,
∵ ∴∠E+∠EAQ=180°,
∵, ∴,
∴∠QAB+∠B=180°,
∵∠EAB=∠EAQ+∠QAB,
∴∠E+∠EAQ+∠QAB+∠B=∠E+∠EAB+∠B=360°;
(2)由(1)知∠E+∠A+∠B=360°,∴∠B=360°-∠E-∠A,
∵∠AEM与∠ABN的角平分线相交于点F,
∴,,
∵, ∴,
∴,
即∠A=2∠EFD;
(3)∵∠AEM与∠ABN的角平分线相交于点F
∴∠AEF=∠FEM, ∠ABF=∠FBG
设∠A=∠BFG=α,∠AEF=∠FEM=β,∠ABF=∠FBG=γ
∵
∴∠EDB=∠FEM=γ
∵FG⊥EF
∴∠EFB+∠BFG=∠EFB+α=90°
∴α=90°-∠EFB
∵∠A+∠AED=∠ABF+EDB
∴α+2β=2γ
∵∠EDB=∠FEM+∠EFB即:γ=β+∠EFB
∴90°-∠EFB+2β=2(β+∠EFB)
∴∠EFB=30°
七年级每日一题109——答案
(1)解:过点P作,如下图.
∵,
∴,
∴,.
∵当秒时,
∴,,
∴;
(2)解:∵,
∴,
∴,
∴(秒);
(3)解:①,
∴(秒);
②,
∴(秒).
综上所述,t的值为18秒或54秒.
七年级每日一题110——答案
(1)直线AB与直线CD平行,理由:
∵EF平分∠AEG,
∴∠AEF=∠GEF,
又∵∠EFG=∠FEG,
∴∠AEF=∠GFE,
∴AB∥CD;
(2)①∵∠HEG=40°,
∴∠FEG=(180°-40°)=70°,
又∵QG平分∠EGH,
∴∠QGH=∠QGE=20°,
∴∠Q=∠FEG-∠EGQ=70°-20°=50°;
②点H在运动过程中,α和β的数量关系不发生变化,
∵∠FEG是△EGQ的外角,∠AEG是△EGH的外角,
∴∠Q=∠FEG-∠EGQ,∠EHG=∠AEG-∠EGH,
又∵FE平分∠AEG,GQ平分∠EGH,
∴∠FEG=∠AEG,∠EGQ=∠EGH,
∴∠Q=∠FEG-∠EGQ
=(∠AEG-∠EGH)
=∠EHG,
即α=β.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
七年级每日一题106——平行线问题的综合探究
班级 姓名 学号
106.若两个角的一组边互相平行,另一组边互相垂直,则称这两个角互为“旁系衍生角”.
(1)如图1,,于点,则与互为“旁系衍生角”.当时,求的度数;
(2)当为锐角时,若与两个角互为“旁系衍生角”,则这两个角的数量关系为________________;
(3)如图2,若,,垂足为点A,,分别平分和,且相交于点,求的度数.
七年级每日一题107——平行线问题的综合探究
班级 姓名 学号
107.如图1,已知,,点E在CD上,点G,F在AB上,点H在AB,CD之间,连接FE,EH,HG,.
(1)求证:;
(2)如图2,FK平分∠AFE交CD于点K,,GM平分∠HGB,若,求∠GHE的度数;
(3)如图3,FK平分∠AFE交CD于点K,,GM平分∠HGB,EM平分∠HED,GM,EM交于点M,若,,求的值.(请直接写出答案)
七年级每日一题108——平行线问题的综合探究
班级 姓名 学号
108.已知.
(1)如图1,求∠E+∠A+∠B的度数,并说明理由.
(2)如图2,∠AEM与∠ABN的角平分线相交于点F.试探究∠EFD与∠A的数量关系,并说明你的理由.
(3)如图3,∠AEM与∠ABN的角平分线相交于点F,过点F作FG⊥EF交BN于点G,若∠A=∠BFG,请直接写出∠EFB的度数.
七年级每日一题109——平行线问题的综合探究
班级 姓名 学号
109.如图1,直线,另一直线分别交AB、CD于M、N,将射线MA绕点M以每秒2°的速度逆时针旋转到,同时射线NC绕点N以每秒3°的速度顺时针旋转到,旋转的时间为t()秒.
(1)如图2,当秒时,射线与相交于点P,求的度数;
(2)如图3,当射线与平行时,求t的值;
(3)当射线与互相垂直时,求t的值.
七年级每日一题110——平行线问题的综合探究
班级 姓名 学号
110.如图甲所示,已知点在直线上,点,在直线上,且,平分.
(1)判断直线与直线是否平行,并说明理由.
(2)如图乙所示,是上点右侧一动点,的平分线交的延长线于点,设,
①若,,求的度数.
②点在运动过程中,请直接写出和的数量关系.
七年级每日一题106——答案
解:∵,
∴∠ADG=90°,
∵,
∴,
∵,
∴.
(2)
或.
(3)
解:∵,
∴,
∵BA⊥AD,
∴∠BAD=90°,
∴,
∴,
∵DE平分∠ADF,
∴,
∵AE平分∠BAC,
∴,
∴,
∴
七年级每日一题107——答案
(1)解:∵,∴.
∵,∴,
∴;
(2)解:如图,过点H作.
∴.
∵,
故可设,则.
∵,
∴,,.
∵FK平分∠AFE,GM平分∠HGB,
∴,,
∴,.
由(1)可知,∴,∴,
解得:.
∴,.
∵,∴,
∴;
(3)解:如图,过点M作.
由题意可设,则.
∵,FK平分∠AFE
∴,.
∵,∴.
∵EM平分∠HED,∴.
∵, ∴,
∴.
∵GM平分∠HGB, ∴,,
∴.
∵, ∴.
∴,即.
由(1)可知,∴,∴.
即,解得:,
∴.
七年级每日一题108——答案
【详解】(1)解:过A作,
∵ ∴∠E+∠EAQ=180°,
∵, ∴,
∴∠QAB+∠B=180°,
∵∠EAB=∠EAQ+∠QAB,
∴∠E+∠EAQ+∠QAB+∠B=∠E+∠EAB+∠B=360°;
(2)由(1)知∠E+∠A+∠B=360°,∴∠B=360°-∠E-∠A,
∵∠AEM与∠ABN的角平分线相交于点F,
∴,,
∵, ∴,
∴,
即∠A=2∠EFD;
(3)∵∠AEM与∠ABN的角平分线相交于点F
∴∠AEF=∠FEM, ∠ABF=∠FBG
设∠A=∠BFG=α,∠AEF=∠FEM=β,∠ABF=∠FBG=γ
∵
∴∠EDB=∠FEM=γ
∵FG⊥EF
∴∠EFB+∠BFG=∠EFB+α=90°
∴α=90°-∠EFB
∵∠A+∠AED=∠ABF+EDB
∴α+2β=2γ
∵∠EDB=∠FEM+∠EFB即:γ=β+∠EFB
∴90°-∠EFB+2β=2(β+∠EFB)
∴∠EFB=30°
七年级每日一题109——答案
(1)解:过点P作,如下图.
∵,
∴,
∴,.
∵当秒时,
∴,,
∴;
(2)解:∵,
∴,
∴,
∴(秒);
(3)解:①,
∴(秒);
②,
∴(秒).
综上所述,t的值为18秒或54秒.
七年级每日一题110——答案
(1)直线AB与直线CD平行,理由:
∵EF平分∠AEG,
∴∠AEF=∠GEF,
又∵∠EFG=∠FEG,
∴∠AEF=∠GFE,
∴AB∥CD;
(2)①∵∠HEG=40°,
∴∠FEG=(180°-40°)=70°,
又∵QG平分∠EGH,
∴∠QGH=∠QGE=20°,
∴∠Q=∠FEG-∠EGQ=70°-20°=50°;
②点H在运动过程中,α和β的数量关系不发生变化,
∵∠FEG是△EGQ的外角,∠AEG是△EGH的外角,
∴∠Q=∠FEG-∠EGQ,∠EHG=∠AEG-∠EGH,
又∵FE平分∠AEG,GQ平分∠EGH,
∴∠FEG=∠AEG,∠EGQ=∠EGH,
∴∠Q=∠FEG-∠EGQ
=(∠AEG-∠EGH)
=∠EHG,
即α=β.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
