浙教版七年级数学每日一题111-115各类应用(含解析)
文档属性
| 名称 | 浙教版七年级数学每日一题111-115各类应用(含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-28 15:45:17 | ||
图片预览





文档简介
中小学教育资源及组卷应用平台
七年级每日一题111——乘法公式的应用
班级 姓名 学号
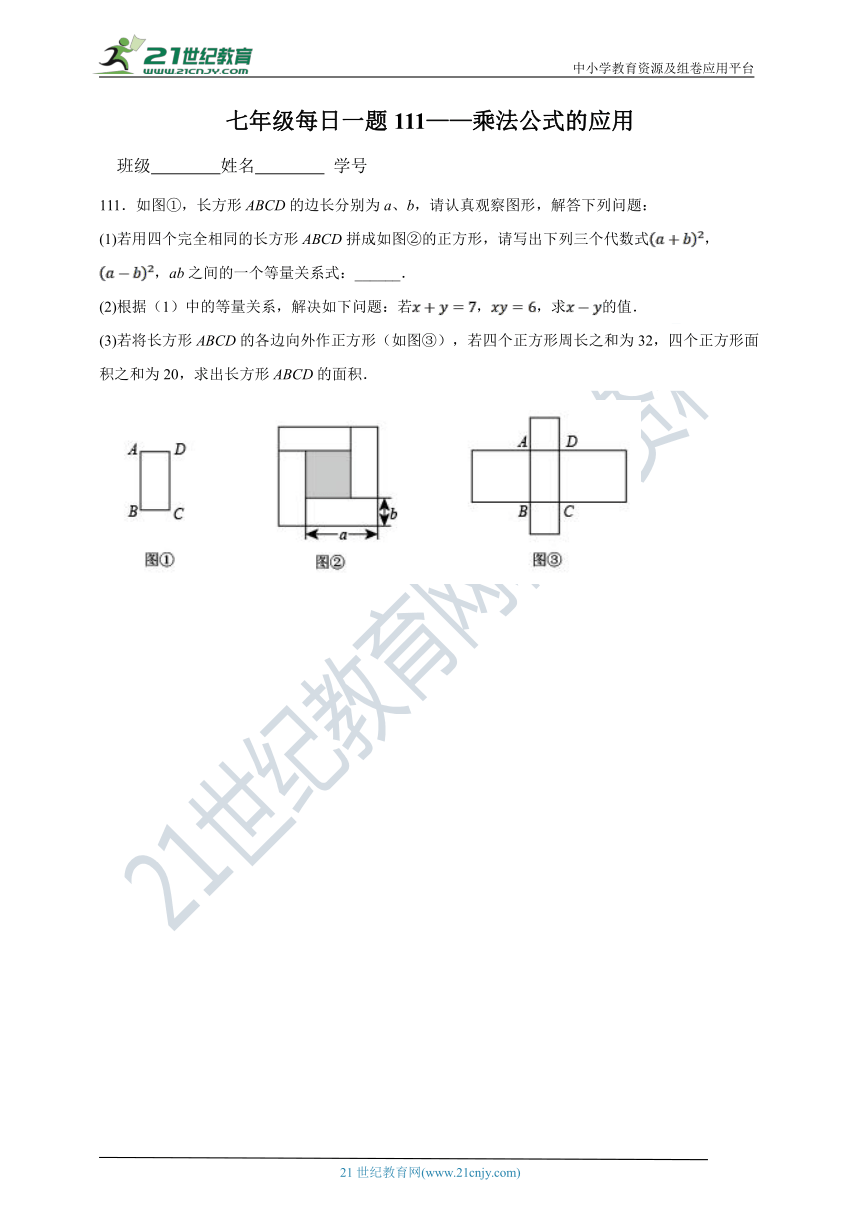
111.如图①,长方形ABCD的边长分别为a、b,请认真观察图形,解答下列问题:
(1)若用四个完全相同的长方形ABCD拼成如图②的正方形,请写出下列三个代数式,,ab之间的一个等量关系式:______.
(2)根据(1)中的等量关系,解决如下问题:若,,求的值.
(3)若将长方形ABCD的各边向外作正方形(如图③),若四个正方形周长之和为32,四个正方形面积之和为20,求出长方形ABCD的面积.
七年级每日一题112——乘法公式的应用
班级 姓名 学号
112.数学活动:认识算两次
把同一个量用两种不同的方法计算两次,进而建立等量关系解决问题,这种方法在数学上称为算两次.例如:在学习整式乘法过程中,我们用两种不同的方法计算如图1中最大的正方形面积验证了完全平方公式:.
(1)如图2,将长为m,宽为n的四个大小、形状完全相同的小长方形按如图所示拼成一个大正方形,用两种不同的方法计算阴影部分的面积可以得出等式______________.
(2)如图3,棱长为x的实心大正方体切除一个棱长为y的小正方体.
①剩余部分按如图所示继续切割为甲、乙、丙三个长方体,它们的体积可以用含x、y的整式分别表示为______________、______________、______________;
②利用①中的结果以及算两次的方法,因式分解:
③若,求的值.
七年级每日一题113——分式的综合应用
班级 姓名 学号
113.我们把形如不为零,且两个解分别为,的方程称为“十字分式方程”.
例如为十字分式方程,可化为 ,,.
再如为十字分式方程,可化为,
,.
应用上面的结论解答下列问题:
(1)若为十字分式方程,则______,______.
(2)若十字分式方程 的两个解分别为,,求的值.
(3)若关于的十字分式方程的两个解分别为,,求的值.
七年级每日一题114——列方程(组)解应用题
班级 姓名 学号
114.杨梅是我市特产水果之一,素有“果中珍品”之美誉!六月,正值杨梅成熟上市的时候.某杨梅基地零售批发“荸荠”,“东魁”两种杨梅.已知零售3斤“荸荠”和5斤“东魁”共需95元;零售5斤“荸荠”和8斤“东魁”共需155元,批发价是在零售价的基础上按下表进行打折:
不超过100斤 100斤~550斤 550斤~1000斤 1000斤~1550斤 1550斤以上
不打折 九五折 九折 八折 七五折
(1)求“荸荠”,“东魁”两种杨梅的零售单价;
(2)某水果商打算用12000元全部用于批发购进“东魁”杨梅,最多能购进多少斤?(不需要写出解答过程,直接写出答案就行)
(3)现用A,B,C三种不同型号的水果箱共30只,将(2)中购得的杨梅进行装箱.装完所有的杨梅时,每只箱子刚好装满.已知A种型号的水果箱每只能装30斤,B种型号的水果箱每只能装50斤,C种型号的水果箱每只能装100斤,为了方便顾客选择,三种不同型号的水果箱都要有.通过计算说明共有几种装箱方案?
七年级每日一题115——列方程(组)解应用题
班级 姓名 学号
115.陈师傅要给一块长6米,宽5米的长方形地面铺瓷砖,如图,现有A和B两种款式的瓷砖,且A款正方形瓷砖的边长与B款长方形瓷砖的长相等,B款瓷砖的长是宽的3倍,已知一块A款瓷砖和一块B款瓷砖的价格和为150元,2块A款瓷砖价格和3块B款瓷砖价格相等,请回答以下问题:
(1)分别求出每款瓷砖的单价;
(2)陈师傅购买瓷砖时,A款瓷砖在以原价8折的价格进行促销活动,结果陈师傅共花了6600元购买两种瓷砖,且两种瓷砖的数量相差不超过20块,则两种瓷砖各买了多少块?
(3)陈师傅打算将长6米,宽5米长方形地面的四周都铺上B款瓷砖,中间部分全部铺上A款瓷砖(如图所示),铺地时B款瓷砖恰好用了52块,则铺地时要用多少块A款地砖?
七年级每日一题111——答案
(1)(a+b)2=(a-b)2+4ab;
图②中,大正方形的边长为a+b,因此面积为(a+b)2,阴影部分是边长为a-b的正方形,因此面积为(a-b)2,周围4个长方形的面积和为4ab,
所以有(a+b)2=(a-b)2+4ab;
(2)∵x+y=7,xy=6,
∴(x-y)2=(x+y)2-4xy=49-24=25,
∴x-y=±5;
(3)设长方形ABCD的长AB=m,宽BC=n,
由四个正方形周长之和为32,四个正方形面积之和为20得,
4m×2+4n×2=32,2m2+2n2=20,
即m+n=4,m2+n2=10,
由(m+n)2=m2+n2+2mn得,
,
即长方形ABCD的面积为3.
七年级每日一题112——答案
(1)由图可知大正方形的边长为(m+n).阴影部分为一个小正方形,且边长为(m-n).
方法一:直接利用正方形面积公式计算:,
方法二:利用大正方形的面积-四个长方形的面积:.
∴得出的等式为.
故答案为:;
(2)①由图可知,甲的体积为:,
乙的体积为:,
丙的体积为:.
故答案为:,,;
②由①可知该几何体的体积为:.
∵该几何体的体积还可用大正方体的体积-挖去的小正方体的体积计算,即,
∴.
③,且.
由②可得:.
∵,且,
∴等号两边可同时除x,即得出,整理,得.
将,等号两边平方,得:,
整理,得:,即.
将,代入,得:.
故.
七年级每日一题113——答案
(1)解:可化为,
,.
(2)解∶ 根据题意得:,,
.
(3)解∶ 原方程变为,
,,
.
七年级每日一题114——答案
(1)解:设“荸荠”杨梅的零售单价为x元,“东魁”杨梅的零售单价为y元,
依题意得:,解得:,
答:“荸荠”杨梅的零售单价为15元,“东魁”杨梅的零售单价为10元;
(2)解:设该水果商购进m斤“东魁”杨梅,
依题意得:10×0.75m≤12000,
解得:m≤1600,
答:该水果商最多能购进1600斤“东魁”杨梅;
(3)解:设需要A种型号的水果箱a只,B种型号的水果箱b只,则需要C种型号的水果箱(30﹣a﹣b)只,
依题意得:30a+50b+100(30﹣a﹣b)=1600,
解得:b=28﹣a,
又∵a,b,(30﹣a﹣b)均为正整数,
∴或或,
答:共有3种装箱方案.
七年级每日一题115——答案
(1)解:设A款地砖每块x元,B款地砖每块y元,
则,所以
答:A款地砖每块90元,B款地砖每块60元.
(2)设A款地砖买了a块,B款地砖买了b块
则,
因为两种瓷砖的数量都相差不超过20块且都为正整数
所以或,或,.
(3)设在长6米的边上铺了B款瓷砖m块,则B款瓷砖的长为米,宽为米,
,
所以长6米的边上铺了8块B款瓷砖,宽5米的边上铺了20块B款瓷砖,
所以中间部分需要用6×6=36块地砖.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
七年级每日一题111——乘法公式的应用
班级 姓名 学号
111.如图①,长方形ABCD的边长分别为a、b,请认真观察图形,解答下列问题:
(1)若用四个完全相同的长方形ABCD拼成如图②的正方形,请写出下列三个代数式,,ab之间的一个等量关系式:______.
(2)根据(1)中的等量关系,解决如下问题:若,,求的值.
(3)若将长方形ABCD的各边向外作正方形(如图③),若四个正方形周长之和为32,四个正方形面积之和为20,求出长方形ABCD的面积.
七年级每日一题112——乘法公式的应用
班级 姓名 学号
112.数学活动:认识算两次
把同一个量用两种不同的方法计算两次,进而建立等量关系解决问题,这种方法在数学上称为算两次.例如:在学习整式乘法过程中,我们用两种不同的方法计算如图1中最大的正方形面积验证了完全平方公式:.
(1)如图2,将长为m,宽为n的四个大小、形状完全相同的小长方形按如图所示拼成一个大正方形,用两种不同的方法计算阴影部分的面积可以得出等式______________.
(2)如图3,棱长为x的实心大正方体切除一个棱长为y的小正方体.
①剩余部分按如图所示继续切割为甲、乙、丙三个长方体,它们的体积可以用含x、y的整式分别表示为______________、______________、______________;
②利用①中的结果以及算两次的方法,因式分解:
③若,求的值.
七年级每日一题113——分式的综合应用
班级 姓名 学号
113.我们把形如不为零,且两个解分别为,的方程称为“十字分式方程”.
例如为十字分式方程,可化为 ,,.
再如为十字分式方程,可化为,
,.
应用上面的结论解答下列问题:
(1)若为十字分式方程,则______,______.
(2)若十字分式方程 的两个解分别为,,求的值.
(3)若关于的十字分式方程的两个解分别为,,求的值.
七年级每日一题114——列方程(组)解应用题
班级 姓名 学号
114.杨梅是我市特产水果之一,素有“果中珍品”之美誉!六月,正值杨梅成熟上市的时候.某杨梅基地零售批发“荸荠”,“东魁”两种杨梅.已知零售3斤“荸荠”和5斤“东魁”共需95元;零售5斤“荸荠”和8斤“东魁”共需155元,批发价是在零售价的基础上按下表进行打折:
不超过100斤 100斤~550斤 550斤~1000斤 1000斤~1550斤 1550斤以上
不打折 九五折 九折 八折 七五折
(1)求“荸荠”,“东魁”两种杨梅的零售单价;
(2)某水果商打算用12000元全部用于批发购进“东魁”杨梅,最多能购进多少斤?(不需要写出解答过程,直接写出答案就行)
(3)现用A,B,C三种不同型号的水果箱共30只,将(2)中购得的杨梅进行装箱.装完所有的杨梅时,每只箱子刚好装满.已知A种型号的水果箱每只能装30斤,B种型号的水果箱每只能装50斤,C种型号的水果箱每只能装100斤,为了方便顾客选择,三种不同型号的水果箱都要有.通过计算说明共有几种装箱方案?
七年级每日一题115——列方程(组)解应用题
班级 姓名 学号
115.陈师傅要给一块长6米,宽5米的长方形地面铺瓷砖,如图,现有A和B两种款式的瓷砖,且A款正方形瓷砖的边长与B款长方形瓷砖的长相等,B款瓷砖的长是宽的3倍,已知一块A款瓷砖和一块B款瓷砖的价格和为150元,2块A款瓷砖价格和3块B款瓷砖价格相等,请回答以下问题:
(1)分别求出每款瓷砖的单价;
(2)陈师傅购买瓷砖时,A款瓷砖在以原价8折的价格进行促销活动,结果陈师傅共花了6600元购买两种瓷砖,且两种瓷砖的数量相差不超过20块,则两种瓷砖各买了多少块?
(3)陈师傅打算将长6米,宽5米长方形地面的四周都铺上B款瓷砖,中间部分全部铺上A款瓷砖(如图所示),铺地时B款瓷砖恰好用了52块,则铺地时要用多少块A款地砖?
七年级每日一题111——答案
(1)(a+b)2=(a-b)2+4ab;
图②中,大正方形的边长为a+b,因此面积为(a+b)2,阴影部分是边长为a-b的正方形,因此面积为(a-b)2,周围4个长方形的面积和为4ab,
所以有(a+b)2=(a-b)2+4ab;
(2)∵x+y=7,xy=6,
∴(x-y)2=(x+y)2-4xy=49-24=25,
∴x-y=±5;
(3)设长方形ABCD的长AB=m,宽BC=n,
由四个正方形周长之和为32,四个正方形面积之和为20得,
4m×2+4n×2=32,2m2+2n2=20,
即m+n=4,m2+n2=10,
由(m+n)2=m2+n2+2mn得,
,
即长方形ABCD的面积为3.
七年级每日一题112——答案
(1)由图可知大正方形的边长为(m+n).阴影部分为一个小正方形,且边长为(m-n).
方法一:直接利用正方形面积公式计算:,
方法二:利用大正方形的面积-四个长方形的面积:.
∴得出的等式为.
故答案为:;
(2)①由图可知,甲的体积为:,
乙的体积为:,
丙的体积为:.
故答案为:,,;
②由①可知该几何体的体积为:.
∵该几何体的体积还可用大正方体的体积-挖去的小正方体的体积计算,即,
∴.
③,且.
由②可得:.
∵,且,
∴等号两边可同时除x,即得出,整理,得.
将,等号两边平方,得:,
整理,得:,即.
将,代入,得:.
故.
七年级每日一题113——答案
(1)解:可化为,
,.
(2)解∶ 根据题意得:,,
.
(3)解∶ 原方程变为,
,,
.
七年级每日一题114——答案
(1)解:设“荸荠”杨梅的零售单价为x元,“东魁”杨梅的零售单价为y元,
依题意得:,解得:,
答:“荸荠”杨梅的零售单价为15元,“东魁”杨梅的零售单价为10元;
(2)解:设该水果商购进m斤“东魁”杨梅,
依题意得:10×0.75m≤12000,
解得:m≤1600,
答:该水果商最多能购进1600斤“东魁”杨梅;
(3)解:设需要A种型号的水果箱a只,B种型号的水果箱b只,则需要C种型号的水果箱(30﹣a﹣b)只,
依题意得:30a+50b+100(30﹣a﹣b)=1600,
解得:b=28﹣a,
又∵a,b,(30﹣a﹣b)均为正整数,
∴或或,
答:共有3种装箱方案.
七年级每日一题115——答案
(1)解:设A款地砖每块x元,B款地砖每块y元,
则,所以
答:A款地砖每块90元,B款地砖每块60元.
(2)设A款地砖买了a块,B款地砖买了b块
则,
因为两种瓷砖的数量都相差不超过20块且都为正整数
所以或,或,.
(3)设在长6米的边上铺了B款瓷砖m块,则B款瓷砖的长为米,宽为米,
,
所以长6米的边上铺了8块B款瓷砖,宽5米的边上铺了20块B款瓷砖,
所以中间部分需要用6×6=36块地砖.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
