浙教版七年级数学每日一题116-120平行线的综合应用及其他
文档属性
| 名称 | 浙教版七年级数学每日一题116-120平行线的综合应用及其他 | 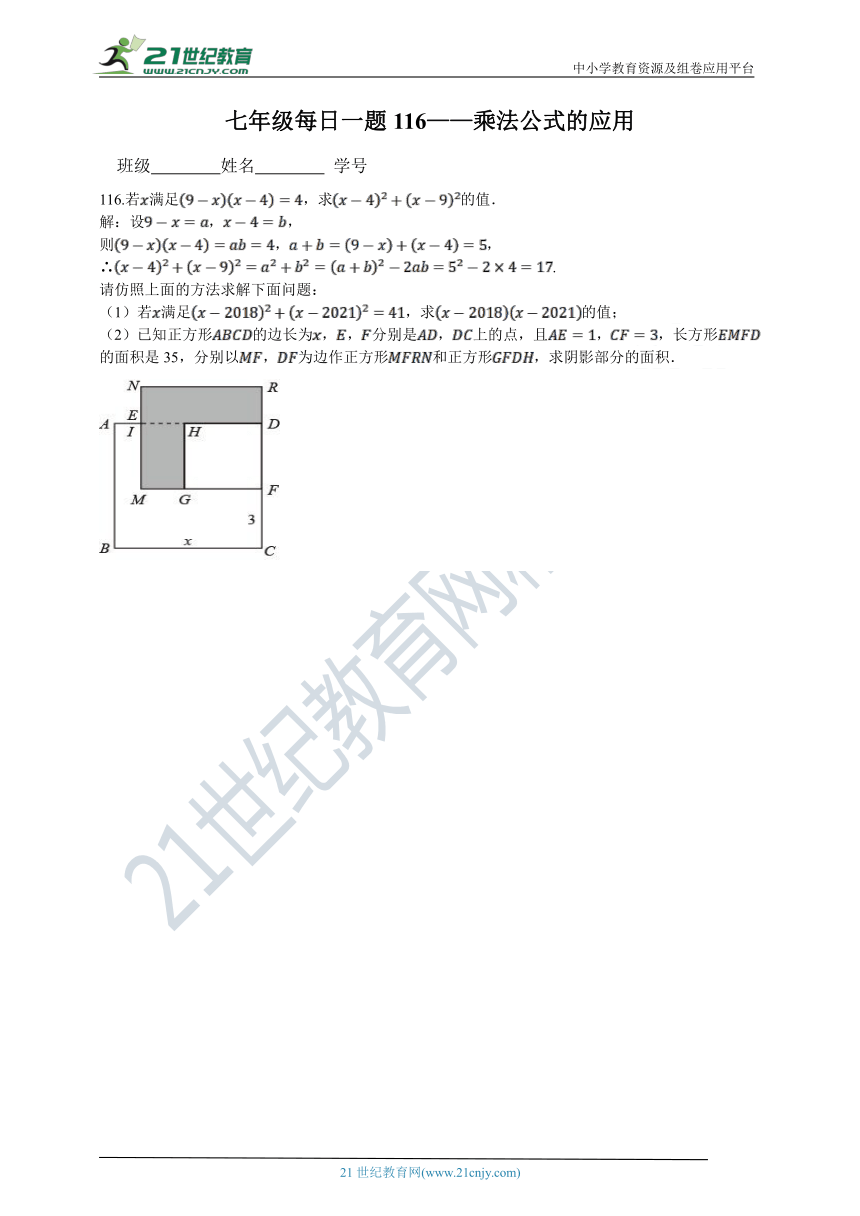 | |
| 格式 | doc | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-28 15:50:39 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
七年级每日一题116——乘法公式的应用
班级 姓名 学号
116.若满足,求的值.
解:设,,
则,,
∴.
请仿照上面的方法求解下面问题:
(1)若满足,求的值;
(2)已知正方形的边长为,,分别是,上的点,且,,长方形的面积是35,分别以,为边作正方形和正方形,求阴影部分的面积.
七年级每日一题117——平行线的综合应用
班级 姓名 学号
117.已知,点在直线,之间,连接,,如图1,易得.
(1)若,请在如图1中画出的角平分线,的角平分线,,两线交于点,利用上述结论,求的度数;
(2)若平分,将线段沿平移至.
①如图2,若,平分,求的度数;
②如图3,若平分,请写出与的数量关系,并说明理由.
七年级每日一题118——平行线的综合应用
班级 姓名 学号
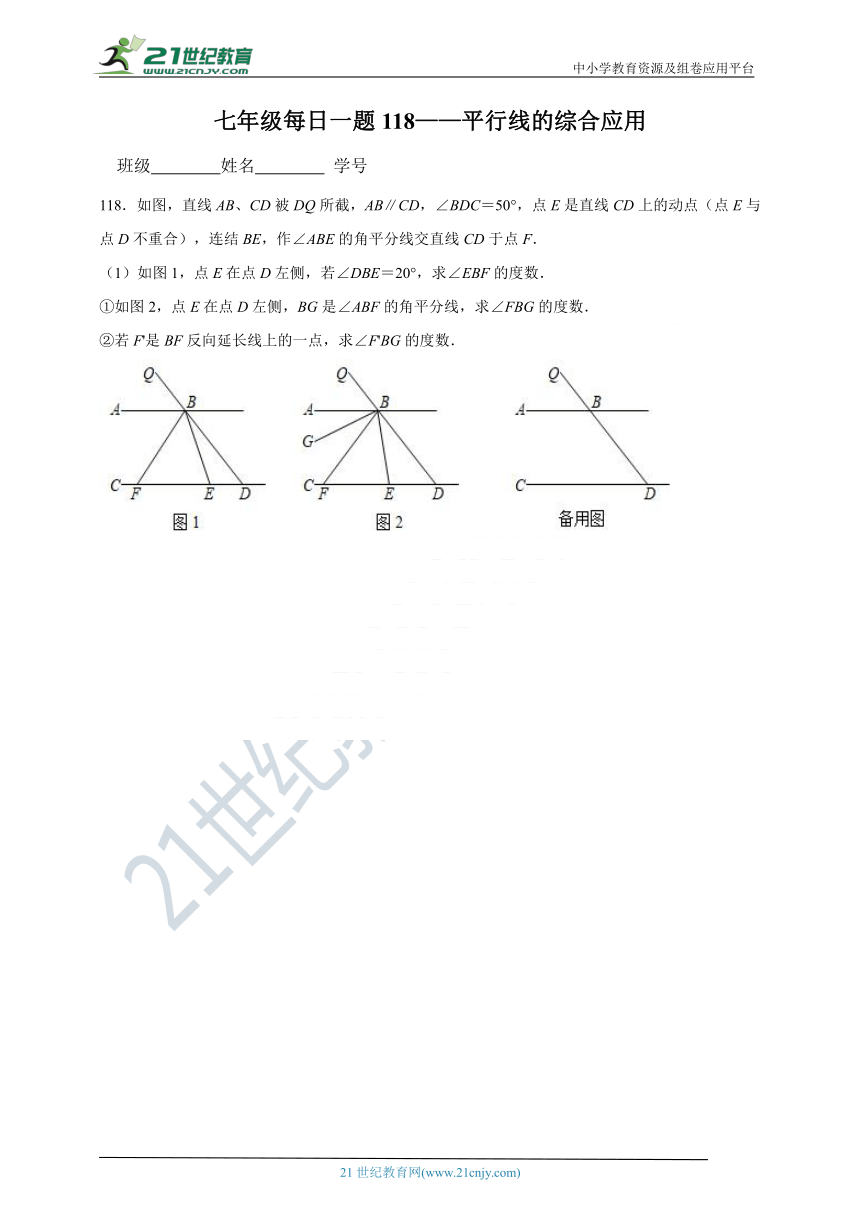
118.如图,直线AB、CD被DQ所截,AB∥CD,∠BDC=50°,点E是直线CD上的动点(点E与点D不重合),连结BE,作∠ABE的角平分线交直线CD于点F.
(1)如图1,点E在点D左侧,若∠DBE=20°,求∠EBF的度数.
①如图2,点E在点D左侧,BG是∠ABF的角平分线,求∠FBG的度数.
②若F'是BF反向延长线上的一点,求∠F'BG的度数.
七年级每日一题119——平行线的综合应用
班级 姓名 学号
119.如图,直线直线,一块三角板的顶点在直线上,边、分别交直线于、两点.,,.
(1)如图1,,则
①______°;
②若与的角平分线交于点,则______°.
(2)如图2,点在的平分线上,连,且,若,求的度数.
(3)如图3,若,,则______°(用含的式子表示).
七年级每日一题120——平行线的综合应用
班级 姓名 学号
120.如图1,在△ABC中,∠B=65°,∠BAC=75°,D为AC边上一点,分别过点A、D作BC、AB的平行线交于点E.
(1)求∠E的度数.
(2)点P为直线AC上的一个动点,过点P作PF∥AE,且PF=AE,连DF.
①如图2,当点P在点C的右侧,且∠PFD=25°时,判断DE与DF的位置关系,并说明理由.
②在整个运动中,是否存在点P,使得∠PFD=2∠EDF?若存在,请求出∠PFD的度数,若不存在,请说明理由.
七年级每日一题116——答案
解:(1)设x-2018=a,x-2021=b,
∴a2+b2=41,a-b=3,
∴-2(x-2018)(x-2021)=-2ab=(a-b)2-(a2+b2)=9-41=-32,
∴(x-2018)(x-2021)=16;
(2)∵正方形ABCD的边长为x,AE=1,CF=3,
∴FM=DE=x-1,DF=x-3,
∴(x-1) (x-3)=35,
∴(x-1)-(x-3)=2,
∴阴影部分的面积=FM2-DF2=(x-1)2-(x-3)2.
设(x-1)=a,(x-3)=b,则(x-1) (x-3)=ab=35,a-b=(x-1)-(x-3)=2,
∴(a+b)2=(a-b)2+4ab=4+140=144,
∵a>0,b>0,
∴a+b>0,
∴a+b=12,
∴(x-1)2-(x-3)2=a2-b2=(a+b) (a-b)=12×2=24.
即阴影部分的面积是24.
七年级每日一题117——答案
【详解】解:(1)如图所示,
过点M作MN∥AB,
∵AB//CD,
∴MN∥AB//CD,
∴∠BAM=∠AMN,∠DCM=∠CMN,
∵AP是∠BAE的角平分线,CQ是∠DCE的角平分线,
∴∠BAM=∠BAE,∠DCM=∠DCE,
即∠AMN=∠BAE,∠CMN=∠DCE,
∵AE⊥CE,
∴∠AEC=90°,
∵∠BAE+∠DCE=∠AEC=90°,
∴∠AMC=∠AMN+∠CMN=∠BAE+∠DCE=(BAE+∠DCE)= 45°;
(2)∵AH平分∠BAE,∴∠BAH=∠EAH,
①∵FH平分∠DFG,
∴设∠GFH=∠DFH=x,
又∵CE∥FG,
∴∠ECD=∠GFD=2x,
又∠AEC=∠BAE+∠DCE=80°,
∴∠BAH=∠EAH=40°-x,
如图,过点H作HI∥AB,
∴∠AHF=∠BAH+∠DFH =40°-x+x=40°;
②∠AHF=90°+∠AEC,理由如下:
设∠GFD=2m,∠BAH=∠EAH=n,
∵FH平分∠CFG,
∴∠GFH=∠CFH== 90°-m,
由(1)知∠AEC=∠BAE+∠DCE=2n+2m,即m+n=∠AEC,
如图,过点H作HJ∥AB,
∴∠AHF-∠AHJ +∠CFH=∠AHF-n +∠CFH= 180°,
即∠AHF-n +90°-m= 180°,
∴∠AHF=90°+(m+n),
∴∠AHF=90°+∠AEC.
七年级每日一题118——答案
【详解】(1)解:如图1,
因为∠BDC=50°,∠DBE=20°,∠BEC是三角形DBE的外角,
所以∠BEC=∠BDC+∠EBD=50°+20°=70°,
因为AB∥CD,
所以∠ABE=180°-70°=110°,
因为∠ABE的角平分线交直线CD于点F,
所以∠EBF=∠ABE=55°,
解:如图2,由(1)可得:∠EBF=∠ABF=55°,
因为BG是∠ABF的角平分线,
所以∠FBG=∠ABF=27.5°;
若F'是BF反向延长线上的一点,则∠F'BG和∠FBG互为邻补角,
所以∠F'BG =180°-∠FBG =180°-27.5°=152.5°.
七年级每日一题119——答案
解:(1)①∵FG//HK
∴∠HAC=∠CEF
∵∠HAC=∠HAB+∠BAC
∴∠HAC=∠CEF=100°
又∵∠FDB=∠CDE,∠CDE+∠C+∠CEF=180°,∠C=30°
∴∠FDB=180°-∠C-∠CEF=50°
② 由① 得∠HAC=100°,∠FDB=∠CDE=50°
∴∠CAK=180°-∠HAC=80°
∵∠CDE与∠CAK的角平分线交于点I
∴∠IDG=∠CDG=25°,∠IAK=∠CAK=40°
∵FG//HK
∴∠IAK=∠EGA=40°
∴∠IGD=180°-∠EGA=140°
∴∠I=180°-∠EGI-∠IDG=15°
(2)由(1)中的② 得∠CAK=80°
∴∠CAI+∠KAI=80°
∵∠CAI:∠KAI=1:3
∴∠KAI=60°
则由(1)中②可以得到∠IGD=120°
∴∠IDG=180°-∠IGD-∠I=25°
∵DI是∠CDG的角平分线
∴∠CDG=2∠IDG=50°
∴∠FDB=∠CDG=50°
(3)由(2)知∠CAI+∠KAI=80°,∠CAI:∠KAI=1: n
∴∠KAI=
∴∠IGD=
由(1)知∠CDE=50°,即∠CDI+∠GDI=50°
∵∠CDI:∠GDI=1: n
∴∠GDI=
∴∠I=180°-∠GDI -∠IGD=
七年级每日一题120——答案
【详解】解:(1)如图1中,
∵AB∥DE,AE∥BC,
∴∠ADE=∠BAC=75°,∠DAE=∠ACB,
∵∠ACB=180°-∠B-∠BAC=180°-65°-75°=40°,
∴∠DAE=∠ACB=40°,
∴∠E=180°-∠ADE-∠EAD=180°-40°-75°=65°.
(2)①如图2中,结论:DE⊥DF.
理由:过点D作DT∥AE.
∵AE∥PF,DT∥AE, ∴AE∥DT∥PF,
∴∠AED=∠TDE,∠TDF=∠DFP,
∴∠EDF=∠TDE+∠TDF=65°+25°=90°, ∴DE⊥DF.
②存在,当点P在点D的左侧时存在.
如图3-1中,当点P在线段AD上时,设DE交PF于J.
∵PF∥AE, ∴∠PJD=∠AED=65°,
∵∠PJD=∠PFD+∠JDF,∠PFD=2∠EDF,
∴65°=3∠EDF, ∴∠EDF=()°, ∴∠PFD=()°.
如图3-2中,当点P在线段DA的延长线上时,设AE交DF于Q.
∵PF∥AE, ∴∠PFD=∠AQD,
∵∠AQD=∠AED+∠EDF,∠PFD=2∠EDF,
∴2∠EDF=65°+∠EDF, ∴∠EDF=65°, ∴∠PFD=130°,
综上所述,∠PFD=()°或130°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
七年级每日一题116——乘法公式的应用
班级 姓名 学号
116.若满足,求的值.
解:设,,
则,,
∴.
请仿照上面的方法求解下面问题:
(1)若满足,求的值;
(2)已知正方形的边长为,,分别是,上的点,且,,长方形的面积是35,分别以,为边作正方形和正方形,求阴影部分的面积.
七年级每日一题117——平行线的综合应用
班级 姓名 学号
117.已知,点在直线,之间,连接,,如图1,易得.
(1)若,请在如图1中画出的角平分线,的角平分线,,两线交于点,利用上述结论,求的度数;
(2)若平分,将线段沿平移至.
①如图2,若,平分,求的度数;
②如图3,若平分,请写出与的数量关系,并说明理由.
七年级每日一题118——平行线的综合应用
班级 姓名 学号
118.如图,直线AB、CD被DQ所截,AB∥CD,∠BDC=50°,点E是直线CD上的动点(点E与点D不重合),连结BE,作∠ABE的角平分线交直线CD于点F.
(1)如图1,点E在点D左侧,若∠DBE=20°,求∠EBF的度数.
①如图2,点E在点D左侧,BG是∠ABF的角平分线,求∠FBG的度数.
②若F'是BF反向延长线上的一点,求∠F'BG的度数.
七年级每日一题119——平行线的综合应用
班级 姓名 学号
119.如图,直线直线,一块三角板的顶点在直线上,边、分别交直线于、两点.,,.
(1)如图1,,则
①______°;
②若与的角平分线交于点,则______°.
(2)如图2,点在的平分线上,连,且,若,求的度数.
(3)如图3,若,,则______°(用含的式子表示).
七年级每日一题120——平行线的综合应用
班级 姓名 学号
120.如图1,在△ABC中,∠B=65°,∠BAC=75°,D为AC边上一点,分别过点A、D作BC、AB的平行线交于点E.
(1)求∠E的度数.
(2)点P为直线AC上的一个动点,过点P作PF∥AE,且PF=AE,连DF.
①如图2,当点P在点C的右侧,且∠PFD=25°时,判断DE与DF的位置关系,并说明理由.
②在整个运动中,是否存在点P,使得∠PFD=2∠EDF?若存在,请求出∠PFD的度数,若不存在,请说明理由.
七年级每日一题116——答案
解:(1)设x-2018=a,x-2021=b,
∴a2+b2=41,a-b=3,
∴-2(x-2018)(x-2021)=-2ab=(a-b)2-(a2+b2)=9-41=-32,
∴(x-2018)(x-2021)=16;
(2)∵正方形ABCD的边长为x,AE=1,CF=3,
∴FM=DE=x-1,DF=x-3,
∴(x-1) (x-3)=35,
∴(x-1)-(x-3)=2,
∴阴影部分的面积=FM2-DF2=(x-1)2-(x-3)2.
设(x-1)=a,(x-3)=b,则(x-1) (x-3)=ab=35,a-b=(x-1)-(x-3)=2,
∴(a+b)2=(a-b)2+4ab=4+140=144,
∵a>0,b>0,
∴a+b>0,
∴a+b=12,
∴(x-1)2-(x-3)2=a2-b2=(a+b) (a-b)=12×2=24.
即阴影部分的面积是24.
七年级每日一题117——答案
【详解】解:(1)如图所示,
过点M作MN∥AB,
∵AB//CD,
∴MN∥AB//CD,
∴∠BAM=∠AMN,∠DCM=∠CMN,
∵AP是∠BAE的角平分线,CQ是∠DCE的角平分线,
∴∠BAM=∠BAE,∠DCM=∠DCE,
即∠AMN=∠BAE,∠CMN=∠DCE,
∵AE⊥CE,
∴∠AEC=90°,
∵∠BAE+∠DCE=∠AEC=90°,
∴∠AMC=∠AMN+∠CMN=∠BAE+∠DCE=(BAE+∠DCE)= 45°;
(2)∵AH平分∠BAE,∴∠BAH=∠EAH,
①∵FH平分∠DFG,
∴设∠GFH=∠DFH=x,
又∵CE∥FG,
∴∠ECD=∠GFD=2x,
又∠AEC=∠BAE+∠DCE=80°,
∴∠BAH=∠EAH=40°-x,
如图,过点H作HI∥AB,
∴∠AHF=∠BAH+∠DFH =40°-x+x=40°;
②∠AHF=90°+∠AEC,理由如下:
设∠GFD=2m,∠BAH=∠EAH=n,
∵FH平分∠CFG,
∴∠GFH=∠CFH== 90°-m,
由(1)知∠AEC=∠BAE+∠DCE=2n+2m,即m+n=∠AEC,
如图,过点H作HJ∥AB,
∴∠AHF-∠AHJ +∠CFH=∠AHF-n +∠CFH= 180°,
即∠AHF-n +90°-m= 180°,
∴∠AHF=90°+(m+n),
∴∠AHF=90°+∠AEC.
七年级每日一题118——答案
【详解】(1)解:如图1,
因为∠BDC=50°,∠DBE=20°,∠BEC是三角形DBE的外角,
所以∠BEC=∠BDC+∠EBD=50°+20°=70°,
因为AB∥CD,
所以∠ABE=180°-70°=110°,
因为∠ABE的角平分线交直线CD于点F,
所以∠EBF=∠ABE=55°,
解:如图2,由(1)可得:∠EBF=∠ABF=55°,
因为BG是∠ABF的角平分线,
所以∠FBG=∠ABF=27.5°;
若F'是BF反向延长线上的一点,则∠F'BG和∠FBG互为邻补角,
所以∠F'BG =180°-∠FBG =180°-27.5°=152.5°.
七年级每日一题119——答案
解:(1)①∵FG//HK
∴∠HAC=∠CEF
∵∠HAC=∠HAB+∠BAC
∴∠HAC=∠CEF=100°
又∵∠FDB=∠CDE,∠CDE+∠C+∠CEF=180°,∠C=30°
∴∠FDB=180°-∠C-∠CEF=50°
② 由① 得∠HAC=100°,∠FDB=∠CDE=50°
∴∠CAK=180°-∠HAC=80°
∵∠CDE与∠CAK的角平分线交于点I
∴∠IDG=∠CDG=25°,∠IAK=∠CAK=40°
∵FG//HK
∴∠IAK=∠EGA=40°
∴∠IGD=180°-∠EGA=140°
∴∠I=180°-∠EGI-∠IDG=15°
(2)由(1)中的② 得∠CAK=80°
∴∠CAI+∠KAI=80°
∵∠CAI:∠KAI=1:3
∴∠KAI=60°
则由(1)中②可以得到∠IGD=120°
∴∠IDG=180°-∠IGD-∠I=25°
∵DI是∠CDG的角平分线
∴∠CDG=2∠IDG=50°
∴∠FDB=∠CDG=50°
(3)由(2)知∠CAI+∠KAI=80°,∠CAI:∠KAI=1: n
∴∠KAI=
∴∠IGD=
由(1)知∠CDE=50°,即∠CDI+∠GDI=50°
∵∠CDI:∠GDI=1: n
∴∠GDI=
∴∠I=180°-∠GDI -∠IGD=
七年级每日一题120——答案
【详解】解:(1)如图1中,
∵AB∥DE,AE∥BC,
∴∠ADE=∠BAC=75°,∠DAE=∠ACB,
∵∠ACB=180°-∠B-∠BAC=180°-65°-75°=40°,
∴∠DAE=∠ACB=40°,
∴∠E=180°-∠ADE-∠EAD=180°-40°-75°=65°.
(2)①如图2中,结论:DE⊥DF.
理由:过点D作DT∥AE.
∵AE∥PF,DT∥AE, ∴AE∥DT∥PF,
∴∠AED=∠TDE,∠TDF=∠DFP,
∴∠EDF=∠TDE+∠TDF=65°+25°=90°, ∴DE⊥DF.
②存在,当点P在点D的左侧时存在.
如图3-1中,当点P在线段AD上时,设DE交PF于J.
∵PF∥AE, ∴∠PJD=∠AED=65°,
∵∠PJD=∠PFD+∠JDF,∠PFD=2∠EDF,
∴65°=3∠EDF, ∴∠EDF=()°, ∴∠PFD=()°.
如图3-2中,当点P在线段DA的延长线上时,设AE交DF于Q.
∵PF∥AE, ∴∠PFD=∠AQD,
∵∠AQD=∠AED+∠EDF,∠PFD=2∠EDF,
∴2∠EDF=65°+∠EDF, ∴∠EDF=65°, ∴∠PFD=130°,
综上所述,∠PFD=()°或130°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
