2.3 解二元一次方程组(2)课件 (17张ppt)
文档属性
| 名称 | 2.3 解二元一次方程组(2)课件 (17张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 327.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 00:00:00 | ||
图片预览






文档简介
2.3 解二元一次方程组(2)
第2章 二元一次方程组
浙教版 七年级下册
课前复习
【2】主要步骤:
4.写解
3.求解
2.代入
把这个未知数的值代入③,求得另一个未知数的值.(并代回原方程进行检验)
写出方程组的解.
1.变形
选取一个方程,将它写成一个未知数表示另一个未知数,记作方程③
把③代入另一个方程,得到一个一元一次方程,解这个一元一次方程,得出一个未知数的值.
【1】基本思路:
二元
一元
用“代入消元法”解二元一次方程组
消元
新知探究
解方程组:
?2x+3y=210 ①
?
2x -3y=30 ②
新知探究
完成这个方程组的求解过程(填空):
解:将方程① ②的左右两边分别相加,得 __________.(依据什么?)
解得 x=_____. 把解得的x的值代入①,得_______________.
解得 y=_____.
所以原方程组的解是__________
4x=240
60
120+3y=210
30
【策略1】当两个方程中同一个未知数的系数互为相反数时,用相加消元.
解方程组:
?2x+3y=210 ①
?
2x -3y=30 ②
新知探究
完成这个方程组的求解过程(填空):
解:将方程① ②的左右两边分别相减,得 __________.(依据什么?)
解得 x=_____. 把解得的x的值代入①,得_______________.
解得 y=_____.
所以原方程组的解是__________
【策略2】当两个方程中同一个未知数的系数相同时,用相减消元.
解方程组:
?2x+3y=210 ①
?
2x -3y=30 ②
30
60
6y=180
2x+90=210
新知学习
【新知】加减消元法
当二元一次方程组的两个方程中同一未知数的系数是互为相反数或相同时,可以通过将两个方程的两边分别相加或相减来消元,从而转化为一元一次方程来求解. 这种解二元一次方程组的方法叫做加减消元法,简称加减法.
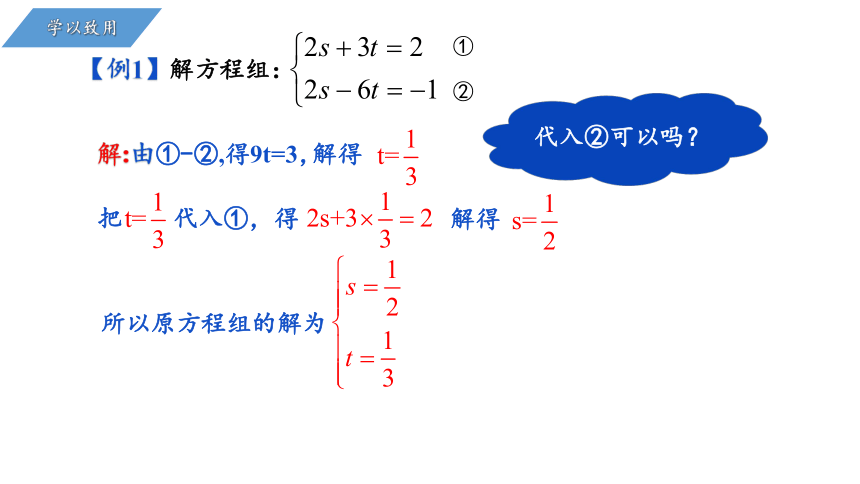
学以致用
①
②
解:由①-②,得9t=3,
【例1】解方程组:
解得
把 代入①,得
解得
所以原方程组的解为
代入②可以吗?
学以致用
解方程组
解:由①+②,得___________,
解得__________
把_____代入①,得__________,
解得__________
所以原方程组的解为__________
学以致用
解:①×___,得______________ ③
②×___,得 _____________ ④
,得_____________
∴__________
把_______代入①,得_____________,
解得y=2
【例2】解方程组
所以原方程组的解为___________
① ②
先消x如何变形?
归纳小结
加减
转化
通过加(减)消去这个未知数,得到一元一次方程
求解
加减消元法的一般步骤:
解这个一元一次方程,得到这个未知数的值
将其中一个未知数的系数化成相同(或是相反数)
代入
将此未知数的值代入原方程,求另一个未知数的值
写解
写出方程组的解(检验)
学以致用
解方程组:
学以致用
解方程组:
解:①× ,得 ____________ ③
②× ,得 ____________ ④
③ ④,得 ____________
∴ ________
把 ________代入①,得 ____________,
解得y=2
所以原方程组的解为 ____________
学以致用
解方程组:
学以致用
学以致用
课堂总结
加减
转化
通过加(减)消去这个未知数,得到一元一次方程
求解
加减消元法的一般步骤:
解这个一元一次方程,得到这个未知数的值
将其中一个未知数的系数化成相同(或是相反数)
代入
将此未知数的值代入原方程,求另一个未知数的值
写解
写出方程组的解(检验)
作业布置
1. 作业本2:2.3 解二元一次方程组(2)
2. 作业订正和自主练习.
第2章 二元一次方程组
浙教版 七年级下册
课前复习
【2】主要步骤:
4.写解
3.求解
2.代入
把这个未知数的值代入③,求得另一个未知数的值.(并代回原方程进行检验)
写出方程组的解.
1.变形
选取一个方程,将它写成一个未知数表示另一个未知数,记作方程③
把③代入另一个方程,得到一个一元一次方程,解这个一元一次方程,得出一个未知数的值.
【1】基本思路:
二元
一元
用“代入消元法”解二元一次方程组
消元
新知探究
解方程组:
?2x+3y=210 ①
?
2x -3y=30 ②
新知探究
完成这个方程组的求解过程(填空):
解:将方程① ②的左右两边分别相加,得 __________.(依据什么?)
解得 x=_____. 把解得的x的值代入①,得_______________.
解得 y=_____.
所以原方程组的解是__________
4x=240
60
120+3y=210
30
【策略1】当两个方程中同一个未知数的系数互为相反数时,用相加消元.
解方程组:
?2x+3y=210 ①
?
2x -3y=30 ②
新知探究
完成这个方程组的求解过程(填空):
解:将方程① ②的左右两边分别相减,得 __________.(依据什么?)
解得 x=_____. 把解得的x的值代入①,得_______________.
解得 y=_____.
所以原方程组的解是__________
【策略2】当两个方程中同一个未知数的系数相同时,用相减消元.
解方程组:
?2x+3y=210 ①
?
2x -3y=30 ②
30
60
6y=180
2x+90=210
新知学习
【新知】加减消元法
当二元一次方程组的两个方程中同一未知数的系数是互为相反数或相同时,可以通过将两个方程的两边分别相加或相减来消元,从而转化为一元一次方程来求解. 这种解二元一次方程组的方法叫做加减消元法,简称加减法.
学以致用
①
②
解:由①-②,得9t=3,
【例1】解方程组:
解得
把 代入①,得
解得
所以原方程组的解为
代入②可以吗?
学以致用
解方程组
解:由①+②,得___________,
解得__________
把_____代入①,得__________,
解得__________
所以原方程组的解为__________
学以致用
解:①×___,得______________ ③
②×___,得 _____________ ④
,得_____________
∴__________
把_______代入①,得_____________,
解得y=2
【例2】解方程组
所以原方程组的解为___________
① ②
先消x如何变形?
归纳小结
加减
转化
通过加(减)消去这个未知数,得到一元一次方程
求解
加减消元法的一般步骤:
解这个一元一次方程,得到这个未知数的值
将其中一个未知数的系数化成相同(或是相反数)
代入
将此未知数的值代入原方程,求另一个未知数的值
写解
写出方程组的解(检验)
学以致用
解方程组:
学以致用
解方程组:
解:①× ,得 ____________ ③
②× ,得 ____________ ④
③ ④,得 ____________
∴ ________
把 ________代入①,得 ____________,
解得y=2
所以原方程组的解为 ____________
学以致用
解方程组:
学以致用
学以致用
课堂总结
加减
转化
通过加(减)消去这个未知数,得到一元一次方程
求解
加减消元法的一般步骤:
解这个一元一次方程,得到这个未知数的值
将其中一个未知数的系数化成相同(或是相反数)
代入
将此未知数的值代入原方程,求另一个未知数的值
写解
写出方程组的解(检验)
作业布置
1. 作业本2:2.3 解二元一次方程组(2)
2. 作业订正和自主练习.
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
