1.1平行线 浙教版初中数学七年级下册专项练习(含解析)
文档属性
| 名称 | 1.1平行线 浙教版初中数学七年级下册专项练习(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-04 06:58:37 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙教版七年级下册数学1.1平行线 专项练习
(考试时间:60分钟 满分:100分)
选择题(本大题共10小题,每小题3分,共30分。下列各题的备选答案中,只有一项是最符合题意的,请选出。)
、为同一平面内的三条直线,若与不平行,与不平行,那么下列判断正确的是( )
与一定不平行
与一定平行
与一定互相垂直
与可能相交或平行
2、有下列说法:
①过一点有且只有一条直线与已知直线平行;
②过一点有且只有一条直线与已知直线垂直;
③在同一平面内的两直线位置关系只有两种:平行或相交;
④在同一平面内,两直线垂直是相交的一种特殊情况.
其中正确的个数是( )
A.1 B.2
C.3 D.4
3、下列语句中正确的个数是( )
①如果两条直线都和第三条直线垂直,那么这两条直线互相平行;
②在同一平面内,不相交的两条直线是平行线;
③在同一平面内,互相垂直的两条线段一定相交;
④在同一平面内,没有公共点的两条直线互相平行.
A.1 B.2 C.3 D.4
4.已知n条(n≥3,且n为整数)直线中只有两条直线平行,且任何三条直线都不交于同一个点。如图,当n=3时,共有2个交点,当n=4时,共有5个交点,当n=5时,共有9个交点….依此规律,当共有交点个数为27时,则n的值为( )
A.6 B.7 C.8 D.9
5.下列说法错误的是( )
A.对顶角相等
B.同角(等角)的余角相等
C.过一点有且只有一条直线与已知直线平行
D.过一点有且只有一条直线与已知直线垂直
6.下列说法不正确的是( )
A.平行于同一条直线的两直线平行
B.从直线外一点向直线所作的垂线段,叫做点到直线的距离
C.等角的补角相等
D.平面内,过一点有且只有一条直线与已知直线垂直
7.如图,已知A为直线l外一定点,B为直线l上一动点.则下列说法正确的是( ).
A.当点B自左向右移动时,A,B两点间的距离越来越小
B.连接AB,则线段AB的长度即为点A到直线l的距离
C.过点A有且只有一条直线与直线l平行
D.同一平面内,过点A有两条直线与直线l垂直
8.下面关于平行线的说法中,正确的个数是 ( )
①在同一平面内,不相交的两条直线必平行
②在同一平面内,不相交的两条线段必平行
③在同一平面内,不平行的两条直线必相交
④在同一平面内,不平行的两条线段必相交
A.0 B.2 C.3 D.4
9.两条平行线间的距离是指( )
A.其中一条直线上的一点到另一条直线的垂线
B.其中一条直线上的一点到另一条直线的垂线的长
C.其中一条直线上的一点到另一条直线的垂线段
D.其中一条直线上的一点到另一条直线的垂线段的长
10.以下说法中,①实数和数轴上的点一一对应;②过直线外一点有且只有一条直线与已知直线垂直;③如果两条直线都和第三条直线平行,那么这两条直线也互相平行;④若一个数的立方根与平方根相同,那么这个数只能是0.其中说法正确的是( )
A.1 B.2 C.3 D.4
填空题(本大题共5小题,每小题4分,共20分。)
11.如图是一个风车的示意图,当 CD 旋转到与地面EF 平行的位置时,AB (填“能”或“不能”)同时与地面 EF 平行。
理由是 。
已知直线a∥b,a与b之间的距离为5,a与b之间有一点P,点P到a的距离是2,则点P到b的距离是_____.
12.a、b、c是直线,且a∥b,b∥c,则________ .
13.如图,在直线外有一点,经过点可以画无数条直线,如果,那么过点的其它直线与直线一定不平行,理由是__________.
14.在∠AOB中,C,D分别为边OA,OB上的点(不与顶点O重合).对于任意锐角∠AOB,下面三个结论中,①作边OB的平行线与边OA相交,这样的平行线能作出无数条;②连接CD,存在∠ODC是直角;③点C到边OB的距离不超过线段CD的长.所有正确结论的序号是________.
15.现有下列说法:
①过一点有且只有一条直线与已知直线垂直;
②过一点有且只有一条直线与已知直线平行;
③若,,则;
④若,的两边与的两边分别平行,则或;
⑤若,,则.
其中正确的是_______(填写序号).
三、解答题(本大题共5小题,每小题10分,共50分。解答应写出文字说明、证明过程或演算步骤.)
16.如图,已知ABC 中,ZBAC=90°根据下列要求画图并回答问题
画BC边上的高AD,过点A画直线AE//BC(不要求写画法和结论)
在 (1)的图形中,如果 BC=a,点B到直线AC 的距离是3,点C到直线 AB 的距离是4,那么直线 AE 与BC 间的距离等于 (用含a的代数式表示)
17.如图,请使用三角板与直尺画图:
(1)过点Р作直线,交ON于点A;
(2)过点Р向OM作垂线,垂足为点C,交ON于点D;
18.已知,如图:
(1)过点B画直线BM∥AC;
(2)延长BC至点D,使CD=BC;
(3)过点A作BC的垂线AN,垂足为点N.
(说明(1)至(3)用直尺或三角板画图,不写画法.)
(4)在前面所作图中,若点N是BC的中点,CN=2cm,则BD的长为______cm
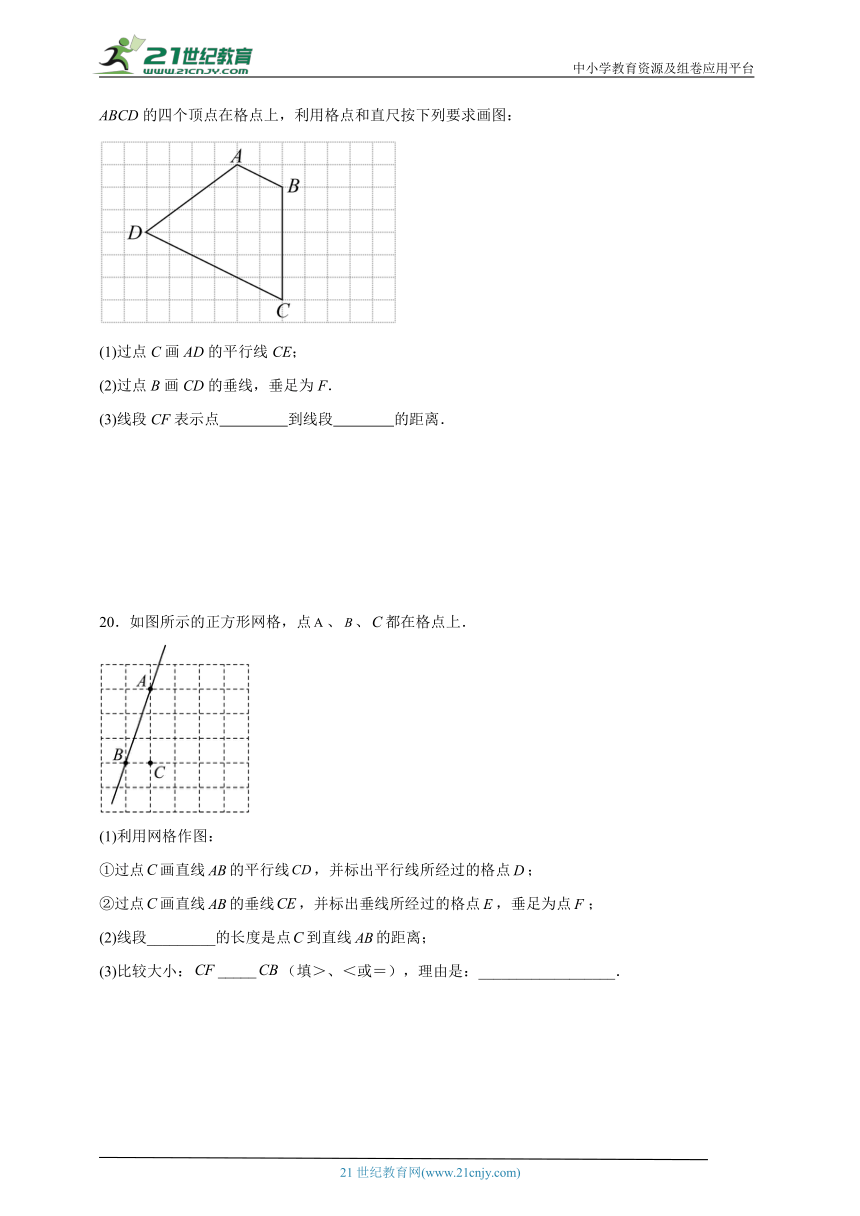
19.在如图所示的方格纸中,每个小正方形的顶点称为格点,每个小正方形的边长为1,已知四边形ABCD的四个顶点在格点上,利用格点和直尺按下列要求画图:
(1)过点C画AD的平行线CE;
(2)过点B画CD的垂线,垂足为F.
(3)线段CF表示点 到线段 的距离.
20.如图所示的正方形网格,点、、都在格点上.
(1)利用网格作图:
①过点画直线的平行线,并标出平行线所经过的格点;
②过点画直线的垂线,并标出垂线所经过的格点,垂足为点;
(2)线段_________的长度是点到直线的距离;
(3)比较大小:(填>、<或=),理由是:__________________.
选择题
1.【答案】 D
【解析】
由题意可得图形:
故选D
2.【答案】 B
3.【答案】 B
4.【答案】 C
【解析】
解:当n=3时,每增加一条直线,交点的个数就增加n-1. 即:
当n=3时,共有2个交点:
当n=4时,共有5个交点;
当n=5时,共有9个交点;
…
n条直线共有交点2+3+4+…+(n-1)= 个
解方程 =27,得n=8或-7(负值舍去).
5.【答案】C
【分析】分别根据对顶角以及平行公理和垂线的性质等知识,分别分析得出即可.
【详解】解:A、对顶角相等,原说法正确,故本选项不符合题意;
B、同角(等角)的余角相等,原说法正确,故本选项不符合题意;
C、过直线外一点有且只有一条直线与已知直线平行,原说法错误,故本选项符合题意;
D、过一点有且只有一条直线与已知直线垂直,原说法正确,故本选项不符合题意;
故选:C
6.【答案】B
【分析】根据平行公理的推论,点到直线的距离,补角的性质,垂线的性质逐一分析即可.
【详解】解:A.平行于同一条直线的两直线平行,正确,不符合题意;
B. 从直线外一点向直线所作的垂线段的长度,叫做点到直线的距离,错误,符合题意;
C. 等角的补角相等,正确,不符合题意;
D. 平面内,过一点有且只有一条直线与已知直线垂直,正确,不符合题意.
7.【答案】C
【分析】根据点到直线的距离,垂线及平行线的性质,依次判断即可.
【详解】解:A、当点B自左向右移动时,A,B两点间的距离先变小后变大,选项错误;
B、当AB⊥l时,线段AB的长度即为点A到直线l的距离,选项错误;
C、过点A有且只有一条直线与直线l平行,选项正确;
D、同一平面内,过点A有一条直线与直线l垂直,选项错误;
故选:C.
8.【答案】B
【分析】根据平面内直线和线段的位置关系判断.
【详解】在同一平面内,不相交的两条直线必平行,不平行的两条直线必相交,
线段则不一定,故①③正确。
故选B
9.【答案】D
【分析】根据平行线间的距离的定义直接进行选择即可.
【详解】解:平行线之间的距离:从一条平行线上的任意一点到另一条直线作垂线,垂线段的长度叫两条平行线之间的距离,
∴A、B、C错误,不符合题意,D正确,符合题意,
故选:D.
10.【答案】D
【分析】根据实数与数轴,垂直与平行,平方根和立方根的概念逐项分析即可.
【详解】①实数和数轴上的点一一对应,该说法正确;
②过直线外一点有且只有一条直线与已知直线垂直,该说法正确;
③如果两条直线都和第三条直线平行,那么这两条直线也互相平行,该说法正确;
④若一个数的立方根与平方根相同,那么这个数只能是0,该说法正确;
故说法正确的有4个.
故选:D.
填空题
11.【答案】 不能
过直线外一点,有且只有一条直线与它平行
12.【答案】3
【分析】根据平行线间的距离与点到直线的距离即可求出.
【详解】解:∵直线a∥b,a与b之间的距离为5,a与b之间有一点P,点P到a的距离是2,
∴点P到b的距离是5﹣2=3,
故答案为3.
13.【答案】a∥c
【分析】根据平行公理推论,即可求解.
【详解】∵a、b、c是直线,且a∥b,b∥c
∴a∥c
故答案为:a∥c
14.【答案】平行公理:经过直线外一点,有且只有一条直线与这条直线平行.
【分析】根据平行公理:经过直线外一点,有且只有一条直线与这条直线平行,解决即可.
【详解】在直线外有一点,经过点可以画无数条直线,但根据平行公理可知,过点P只有一条直线平行,既然如果,那么过点的其它直线与直线一定不平行.
故答案是:平行公理:经过直线外一点,有且只有一条直线与这条直线平行.
15.【答案】①②③
【分析】根据题中描述,作图判断即可得出答案.
【详解】解:①作边OB的平行线与边OA相交,因为OA为射线,所以这样的平行线能作出无数条,所以①正确;
②连接CD,∠ODC的大小不确定,但一定存在∠ODC是直角的情况,所以②正确;
③CD可看作是点C到射线OB上任意一点的连线,则点C到边OB的距离一定小于等于CD的长,所以③正确;
故答案为:①②③.
解答题
16.【答案】 (1)
(2)
【解析】
(2)∵△ABC 中∠BAC=90°,即AB⊥AC,
又点B到直线AC的距离是3,即 AB =3;
点C到直线 4B 的距离是4,即AC =4
又△ABC的面积AB × AC÷2=BC ×AD÷2 ,BC=a
∴AD=
∵AE//BC,AD⊥BC
∴直线AE与BC之间的距离等于
17.【答案】(1)作图见详解;
(2)作图将详解;
【分析】(1)先将三角尺的一直角边紧靠直线OM,边缘与OM重合,再将三角尺的另一条直角边紧贴直尺的一边,最后向上移动三角尺,画一条平行线.
(2)先将直尺与OM重合,再反向延长OM,再将三角板一直角边与直尺重合,再移动三角板使另一直角边过点P,最后过三角板的直角边画CM的垂线.
(1)
解:如图所示:
步骤:(1)将三角尺的一直角边紧靠直线OM,边缘与OM重合,
(2)将三角尺的另一条直角边紧贴直尺的一边,
(3)向下移动三角尺,再次画下一条平行线.
(2)
解:如图所示:
步骤:
(1)将直尺与OM重合,
(2)反向延长OM,
(3)将三角板一直角边与直尺重合,
(4)移动三角板使另一直角边过点P,
(5)过三角板的直角边画CM的垂线.
18.【答案】(1)见解析
(2)见解析
(3)见解析
(4)8
【分析】(1)根据平行线的定义画出图形即可;
(2)根据要求画出图形即可;
(3)根据垂线段的定义画出图形即可;
(4)根据线段中点的定义求解即可.
(1)
解:如图,直线BM即为所求;
(2)
解:如图,线段CD即为所求;
(3)
解:如图,线段AN即为所求;
(4)
解:∵点N是BC的中点,CN=2cm,
∴BN=CN=2cm,
∴BC=4cm,
∴CD=BC=4cm,
∴BD=BC+CD=8cm.
故答案为:8
19.【答案】(1)见解析
(2)见解析
(3)C,BF;
【分析】(1)根据平行线的判定画出图形即可;
(2)根据垂线的定义画出图形即可;
(3)根据点到直线的距离的定义,画出图形即可.
【详解】(1)解:如图,直线CE即为所求;
(2)解:如图,直线BF即为所求;
(3)解:线段CF的长表示点C到线段BF的距离.
故答案为:C,BF;
20.【答案】(1)详见解析
(2)
(3),垂线段最短
【分析】(1)根据平行线的定义及垂线定义,按要求作图即可.
(2)根据点到直线的距离的定义可得线段的长度是点到直线的距离.
(3)根据垂线段最短可以作出判断.
(1)
解:①的平行线如图所示;
②的垂线如图所示;
(2)
解:线段的长度是点到直线的距离,
故答案是:CF;
(3)
解:.理由是:垂线段最短.
故答案是:<,垂线段最短.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
浙教版七年级下册数学1.1平行线 专项练习
(考试时间:60分钟 满分:100分)
选择题(本大题共10小题,每小题3分,共30分。下列各题的备选答案中,只有一项是最符合题意的,请选出。)
、为同一平面内的三条直线,若与不平行,与不平行,那么下列判断正确的是( )
与一定不平行
与一定平行
与一定互相垂直
与可能相交或平行
2、有下列说法:
①过一点有且只有一条直线与已知直线平行;
②过一点有且只有一条直线与已知直线垂直;
③在同一平面内的两直线位置关系只有两种:平行或相交;
④在同一平面内,两直线垂直是相交的一种特殊情况.
其中正确的个数是( )
A.1 B.2
C.3 D.4
3、下列语句中正确的个数是( )
①如果两条直线都和第三条直线垂直,那么这两条直线互相平行;
②在同一平面内,不相交的两条直线是平行线;
③在同一平面内,互相垂直的两条线段一定相交;
④在同一平面内,没有公共点的两条直线互相平行.
A.1 B.2 C.3 D.4
4.已知n条(n≥3,且n为整数)直线中只有两条直线平行,且任何三条直线都不交于同一个点。如图,当n=3时,共有2个交点,当n=4时,共有5个交点,当n=5时,共有9个交点….依此规律,当共有交点个数为27时,则n的值为( )
A.6 B.7 C.8 D.9
5.下列说法错误的是( )
A.对顶角相等
B.同角(等角)的余角相等
C.过一点有且只有一条直线与已知直线平行
D.过一点有且只有一条直线与已知直线垂直
6.下列说法不正确的是( )
A.平行于同一条直线的两直线平行
B.从直线外一点向直线所作的垂线段,叫做点到直线的距离
C.等角的补角相等
D.平面内,过一点有且只有一条直线与已知直线垂直
7.如图,已知A为直线l外一定点,B为直线l上一动点.则下列说法正确的是( ).
A.当点B自左向右移动时,A,B两点间的距离越来越小
B.连接AB,则线段AB的长度即为点A到直线l的距离
C.过点A有且只有一条直线与直线l平行
D.同一平面内,过点A有两条直线与直线l垂直
8.下面关于平行线的说法中,正确的个数是 ( )
①在同一平面内,不相交的两条直线必平行
②在同一平面内,不相交的两条线段必平行
③在同一平面内,不平行的两条直线必相交
④在同一平面内,不平行的两条线段必相交
A.0 B.2 C.3 D.4
9.两条平行线间的距离是指( )
A.其中一条直线上的一点到另一条直线的垂线
B.其中一条直线上的一点到另一条直线的垂线的长
C.其中一条直线上的一点到另一条直线的垂线段
D.其中一条直线上的一点到另一条直线的垂线段的长
10.以下说法中,①实数和数轴上的点一一对应;②过直线外一点有且只有一条直线与已知直线垂直;③如果两条直线都和第三条直线平行,那么这两条直线也互相平行;④若一个数的立方根与平方根相同,那么这个数只能是0.其中说法正确的是( )
A.1 B.2 C.3 D.4
填空题(本大题共5小题,每小题4分,共20分。)
11.如图是一个风车的示意图,当 CD 旋转到与地面EF 平行的位置时,AB (填“能”或“不能”)同时与地面 EF 平行。
理由是 。
已知直线a∥b,a与b之间的距离为5,a与b之间有一点P,点P到a的距离是2,则点P到b的距离是_____.
12.a、b、c是直线,且a∥b,b∥c,则________ .
13.如图,在直线外有一点,经过点可以画无数条直线,如果,那么过点的其它直线与直线一定不平行,理由是__________.
14.在∠AOB中,C,D分别为边OA,OB上的点(不与顶点O重合).对于任意锐角∠AOB,下面三个结论中,①作边OB的平行线与边OA相交,这样的平行线能作出无数条;②连接CD,存在∠ODC是直角;③点C到边OB的距离不超过线段CD的长.所有正确结论的序号是________.
15.现有下列说法:
①过一点有且只有一条直线与已知直线垂直;
②过一点有且只有一条直线与已知直线平行;
③若,,则;
④若,的两边与的两边分别平行,则或;
⑤若,,则.
其中正确的是_______(填写序号).
三、解答题(本大题共5小题,每小题10分,共50分。解答应写出文字说明、证明过程或演算步骤.)
16.如图,已知ABC 中,ZBAC=90°根据下列要求画图并回答问题
画BC边上的高AD,过点A画直线AE//BC(不要求写画法和结论)
在 (1)的图形中,如果 BC=a,点B到直线AC 的距离是3,点C到直线 AB 的距离是4,那么直线 AE 与BC 间的距离等于 (用含a的代数式表示)
17.如图,请使用三角板与直尺画图:
(1)过点Р作直线,交ON于点A;
(2)过点Р向OM作垂线,垂足为点C,交ON于点D;
18.已知,如图:
(1)过点B画直线BM∥AC;
(2)延长BC至点D,使CD=BC;
(3)过点A作BC的垂线AN,垂足为点N.
(说明(1)至(3)用直尺或三角板画图,不写画法.)
(4)在前面所作图中,若点N是BC的中点,CN=2cm,则BD的长为______cm
19.在如图所示的方格纸中,每个小正方形的顶点称为格点,每个小正方形的边长为1,已知四边形ABCD的四个顶点在格点上,利用格点和直尺按下列要求画图:
(1)过点C画AD的平行线CE;
(2)过点B画CD的垂线,垂足为F.
(3)线段CF表示点 到线段 的距离.
20.如图所示的正方形网格,点、、都在格点上.
(1)利用网格作图:
①过点画直线的平行线,并标出平行线所经过的格点;
②过点画直线的垂线,并标出垂线所经过的格点,垂足为点;
(2)线段_________的长度是点到直线的距离;
(3)比较大小:(填>、<或=),理由是:__________________.
选择题
1.【答案】 D
【解析】
由题意可得图形:
故选D
2.【答案】 B
3.【答案】 B
4.【答案】 C
【解析】
解:当n=3时,每增加一条直线,交点的个数就增加n-1. 即:
当n=3时,共有2个交点:
当n=4时,共有5个交点;
当n=5时,共有9个交点;
…
n条直线共有交点2+3+4+…+(n-1)= 个
解方程 =27,得n=8或-7(负值舍去).
5.【答案】C
【分析】分别根据对顶角以及平行公理和垂线的性质等知识,分别分析得出即可.
【详解】解:A、对顶角相等,原说法正确,故本选项不符合题意;
B、同角(等角)的余角相等,原说法正确,故本选项不符合题意;
C、过直线外一点有且只有一条直线与已知直线平行,原说法错误,故本选项符合题意;
D、过一点有且只有一条直线与已知直线垂直,原说法正确,故本选项不符合题意;
故选:C
6.【答案】B
【分析】根据平行公理的推论,点到直线的距离,补角的性质,垂线的性质逐一分析即可.
【详解】解:A.平行于同一条直线的两直线平行,正确,不符合题意;
B. 从直线外一点向直线所作的垂线段的长度,叫做点到直线的距离,错误,符合题意;
C. 等角的补角相等,正确,不符合题意;
D. 平面内,过一点有且只有一条直线与已知直线垂直,正确,不符合题意.
7.【答案】C
【分析】根据点到直线的距离,垂线及平行线的性质,依次判断即可.
【详解】解:A、当点B自左向右移动时,A,B两点间的距离先变小后变大,选项错误;
B、当AB⊥l时,线段AB的长度即为点A到直线l的距离,选项错误;
C、过点A有且只有一条直线与直线l平行,选项正确;
D、同一平面内,过点A有一条直线与直线l垂直,选项错误;
故选:C.
8.【答案】B
【分析】根据平面内直线和线段的位置关系判断.
【详解】在同一平面内,不相交的两条直线必平行,不平行的两条直线必相交,
线段则不一定,故①③正确。
故选B
9.【答案】D
【分析】根据平行线间的距离的定义直接进行选择即可.
【详解】解:平行线之间的距离:从一条平行线上的任意一点到另一条直线作垂线,垂线段的长度叫两条平行线之间的距离,
∴A、B、C错误,不符合题意,D正确,符合题意,
故选:D.
10.【答案】D
【分析】根据实数与数轴,垂直与平行,平方根和立方根的概念逐项分析即可.
【详解】①实数和数轴上的点一一对应,该说法正确;
②过直线外一点有且只有一条直线与已知直线垂直,该说法正确;
③如果两条直线都和第三条直线平行,那么这两条直线也互相平行,该说法正确;
④若一个数的立方根与平方根相同,那么这个数只能是0,该说法正确;
故说法正确的有4个.
故选:D.
填空题
11.【答案】 不能
过直线外一点,有且只有一条直线与它平行
12.【答案】3
【分析】根据平行线间的距离与点到直线的距离即可求出.
【详解】解:∵直线a∥b,a与b之间的距离为5,a与b之间有一点P,点P到a的距离是2,
∴点P到b的距离是5﹣2=3,
故答案为3.
13.【答案】a∥c
【分析】根据平行公理推论,即可求解.
【详解】∵a、b、c是直线,且a∥b,b∥c
∴a∥c
故答案为:a∥c
14.【答案】平行公理:经过直线外一点,有且只有一条直线与这条直线平行.
【分析】根据平行公理:经过直线外一点,有且只有一条直线与这条直线平行,解决即可.
【详解】在直线外有一点,经过点可以画无数条直线,但根据平行公理可知,过点P只有一条直线平行,既然如果,那么过点的其它直线与直线一定不平行.
故答案是:平行公理:经过直线外一点,有且只有一条直线与这条直线平行.
15.【答案】①②③
【分析】根据题中描述,作图判断即可得出答案.
【详解】解:①作边OB的平行线与边OA相交,因为OA为射线,所以这样的平行线能作出无数条,所以①正确;
②连接CD,∠ODC的大小不确定,但一定存在∠ODC是直角的情况,所以②正确;
③CD可看作是点C到射线OB上任意一点的连线,则点C到边OB的距离一定小于等于CD的长,所以③正确;
故答案为:①②③.
解答题
16.【答案】 (1)
(2)
【解析】
(2)∵△ABC 中∠BAC=90°,即AB⊥AC,
又点B到直线AC的距离是3,即 AB =3;
点C到直线 4B 的距离是4,即AC =4
又△ABC的面积AB × AC÷2=BC ×AD÷2 ,BC=a
∴AD=
∵AE//BC,AD⊥BC
∴直线AE与BC之间的距离等于
17.【答案】(1)作图见详解;
(2)作图将详解;
【分析】(1)先将三角尺的一直角边紧靠直线OM,边缘与OM重合,再将三角尺的另一条直角边紧贴直尺的一边,最后向上移动三角尺,画一条平行线.
(2)先将直尺与OM重合,再反向延长OM,再将三角板一直角边与直尺重合,再移动三角板使另一直角边过点P,最后过三角板的直角边画CM的垂线.
(1)
解:如图所示:
步骤:(1)将三角尺的一直角边紧靠直线OM,边缘与OM重合,
(2)将三角尺的另一条直角边紧贴直尺的一边,
(3)向下移动三角尺,再次画下一条平行线.
(2)
解:如图所示:
步骤:
(1)将直尺与OM重合,
(2)反向延长OM,
(3)将三角板一直角边与直尺重合,
(4)移动三角板使另一直角边过点P,
(5)过三角板的直角边画CM的垂线.
18.【答案】(1)见解析
(2)见解析
(3)见解析
(4)8
【分析】(1)根据平行线的定义画出图形即可;
(2)根据要求画出图形即可;
(3)根据垂线段的定义画出图形即可;
(4)根据线段中点的定义求解即可.
(1)
解:如图,直线BM即为所求;
(2)
解:如图,线段CD即为所求;
(3)
解:如图,线段AN即为所求;
(4)
解:∵点N是BC的中点,CN=2cm,
∴BN=CN=2cm,
∴BC=4cm,
∴CD=BC=4cm,
∴BD=BC+CD=8cm.
故答案为:8
19.【答案】(1)见解析
(2)见解析
(3)C,BF;
【分析】(1)根据平行线的判定画出图形即可;
(2)根据垂线的定义画出图形即可;
(3)根据点到直线的距离的定义,画出图形即可.
【详解】(1)解:如图,直线CE即为所求;
(2)解:如图,直线BF即为所求;
(3)解:线段CF的长表示点C到线段BF的距离.
故答案为:C,BF;
20.【答案】(1)详见解析
(2)
(3),垂线段最短
【分析】(1)根据平行线的定义及垂线定义,按要求作图即可.
(2)根据点到直线的距离的定义可得线段的长度是点到直线的距离.
(3)根据垂线段最短可以作出判断.
(1)
解:①的平行线如图所示;
②的垂线如图所示;
(2)
解:线段的长度是点到直线的距离,
故答案是:CF;
(3)
解:.理由是:垂线段最短.
故答案是:<,垂线段最短.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
