浙教版七下专题1.3 图形的平移-重难点题型(含解析)
文档属性
| 名称 | 浙教版七下专题1.3 图形的平移-重难点题型(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-05 07:59:23 | ||
图片预览


文档简介
图形的平移6大题型
【知识点1 平移的定义】
1.图形的平移必须具备两个要素:平移的方向与平移的距离.其中,平移的方向是平移前图形上的某一点到其对应点所指的方向;平移的距离是平移前图形上的某一点到其对应点之间的距离.
2.平移只改变位置,形状与大小都不改变。
【题型1 平移的定义】
【例1】(2023春 扬州期末)下列图形中哪一个图形不能由平移得到( )
A. B. C. D.
【变式1-1】(2023春 临西县期末)下列各组图形可以通过平移互相得到的是( )
A. B.
C. D.
【变式1-2】(2023春 包河区期末)下列几种运动中属于平移的有( )
①水平运输带上砖的运动;
②笔直的铁路上行驶的动车(忽略车轮的转动);
③升降机上下做机械运动;
④足球场上足球的运动.
A.4种 B.3种 C.2种 D.1种
【变式1-3】(2023春 龙岗区期末)在以下现象中:①用打气筒打气时,气筒里活塞的运动;②传送带上,瓶装饮料的移动;③在笔直的公路上行驶的汽车;④温度计中,液柱的上升或下降;⑤钟摆的摆动.属于平移的是( )
A.① B.①② C.①②③ D.①②③④
【知识点2 平移的性质】
(1)平移得到的图形与原图形中的对应线段平行(或在同一条直线上)且相等;对应角相等;对应点的连线平行(或共线)且相等;
(2)“将一个图形沿某一个方向移动一定的距离”意味着“图形上的每一个点都沿同一方向移动了相同的距离”。
【题型2 利用平移的性质解长度问题】
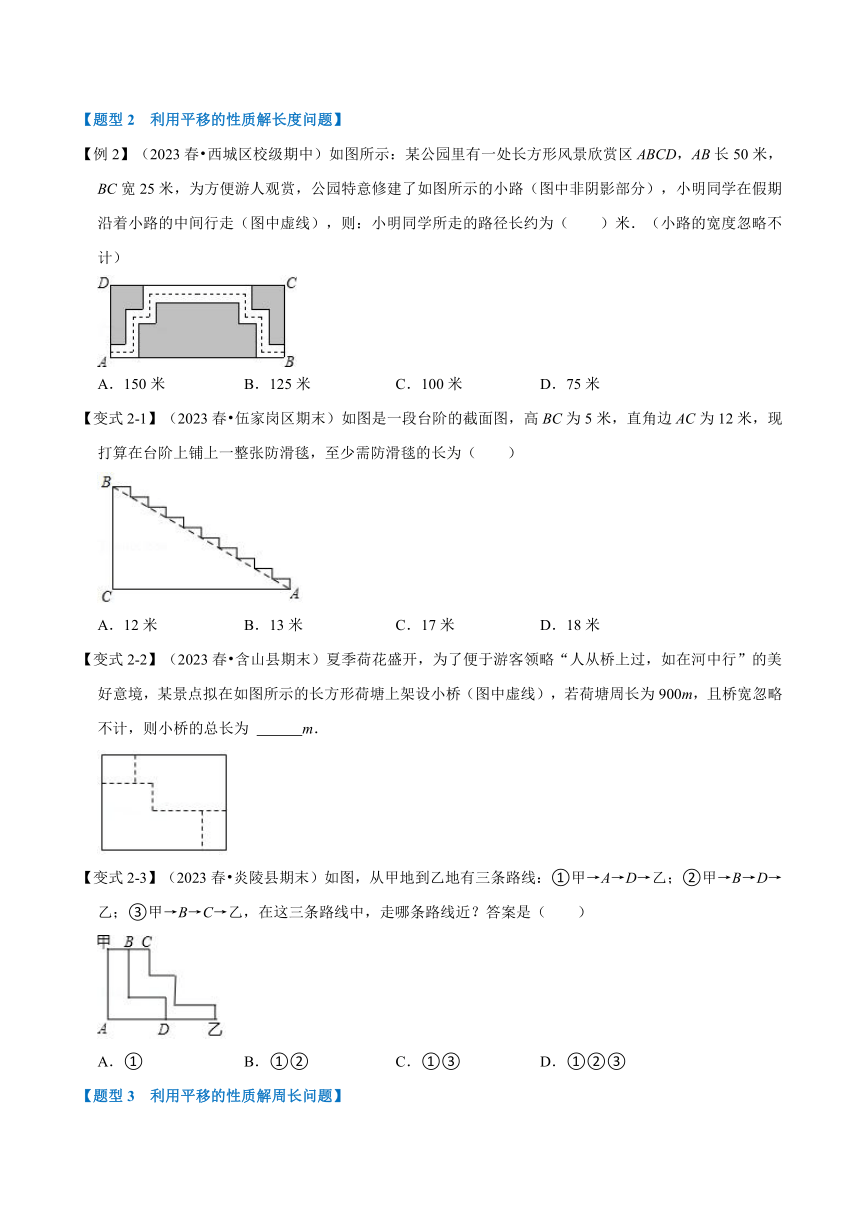
【例2】(2023春 西城区校级期中)如图所示:某公园里有一处长方形风景欣赏区ABCD,AB长50米,BC宽25米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小明同学在假期沿着小路的中间行走(图中虚线),则:小明同学所走的路径长约为( )米.(小路的宽度忽略不计)
A.150米 B.125米 C.100米 D.75米
【变式2-1】(2023春 伍家岗区期末)如图是一段台阶的截面图,高BC为5米,直角边AC为12米,现打算在台阶上铺上一整张防滑毯,至少需防滑毯的长为( )
A.12米 B.13米 C.17米 D.18米
【变式2-2】(2023春 含山县期末)夏季荷花盛开,为了便于游客领略“人从桥上过,如在河中行”的美好意境,某景点拟在如图所示的长方形荷塘上架设小桥(图中虚线),若荷塘周长为900m,且桥宽忽略不计,则小桥的总长为 m.
【变式2-3】(2023春 炎陵县期末)如图,从甲地到乙地有三条路线:①甲→A→D→乙;②甲→B→D→乙;③甲→B→C→乙,在这三条路线中,走哪条路线近?答案是( )
A.① B.①② C.①③ D.①②③
【题型3 利用平移的性质解周长问题】
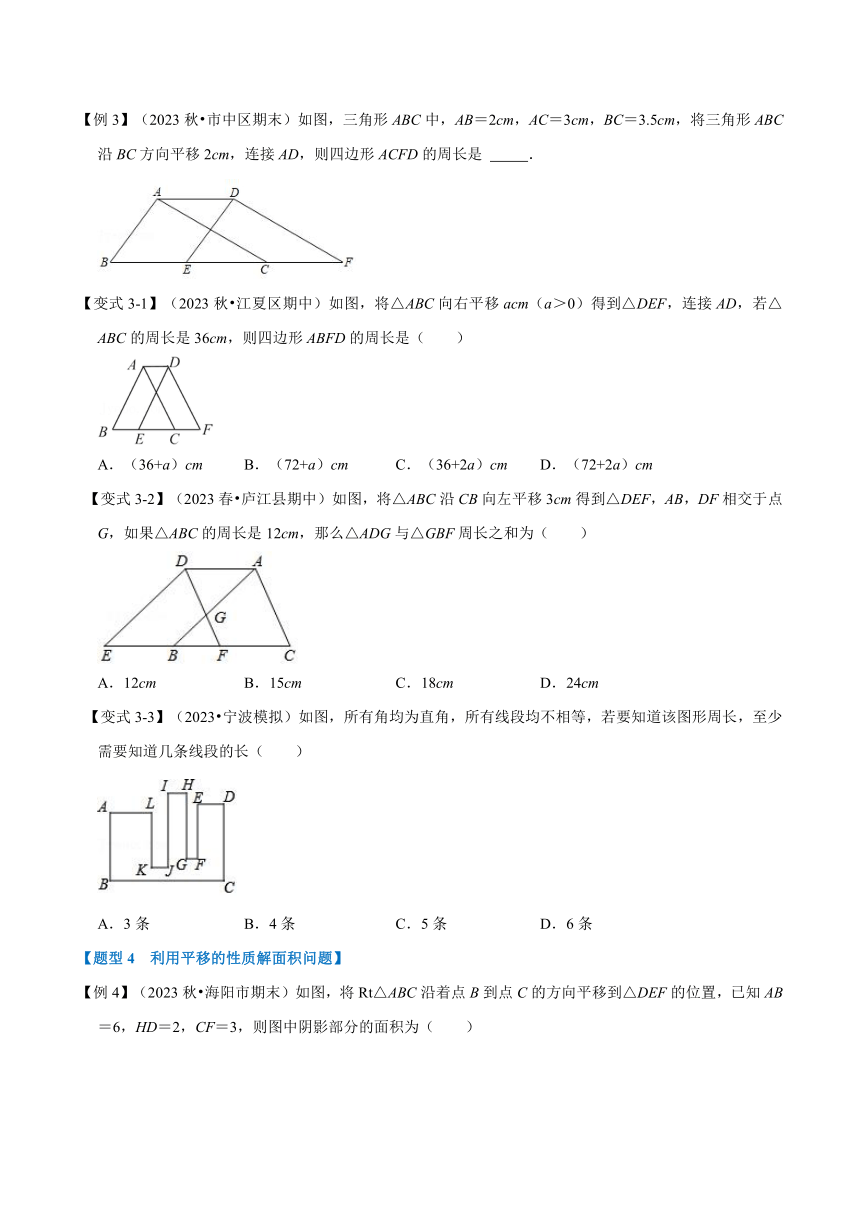
【例3】(2023秋 市中区期末)如图,三角形ABC中,AB=2cm,AC=3cm,BC=3.5cm,将三角形ABC沿BC方向平移2cm,连接AD,则四边形ACFD的周长是 .
【变式3-1】(2023秋 江夏区期中)如图,将△ABC向右平移acm(a>0)得到△DEF,连接AD,若△ABC的周长是36cm,则四边形ABFD的周长是( )
A.(36+a)cm B.(72+a)cm C.(36+2a)cm D.(72+2a)cm
【变式3-2】(2023春 庐江县期中)如图,将△ABC沿CB向左平移3cm得到△DEF,AB,DF相交于点G,如果△ABC的周长是12cm,那么△ADG与△GBF周长之和为( )
A.12cm B.15cm C.18cm D.24cm
【变式3-3】(2023 宁波模拟)如图,所有角均为直角,所有线段均不相等,若要知道该图形周长,至少需要知道几条线段的长( )
A.3条 B.4条 C.5条 D.6条
【题型4 利用平移的性质解面积问题】
【例4】(2023秋 海阳市期末)如图,将Rt△ABC沿着点B到点C的方向平移到△DEF的位置,已知AB=6,HD=2,CF=3,则图中阴影部分的面积为( )
A.12 B.15 C.18 D.24
【变式4-1】(2023春 市中区期末)如图,在△ABC中,∠B=90°,AB=10.将△ABC沿着BC的方向平移至△DEF,若平移的距离是5,则图中阴影部分的面积为( )
A.25 B.50 C.35 D.70
【变式4-2】(2023春 和平区校级月考)如图,一块形状为长方形ABCD的场地,长AB=98米,宽AD=46米,A、B两处入口E小路宽都为1米,两小路汇合处路口宽2米,其余部分种植草坪,那么草坪的面积为( )
A.4320平方米 B.4410平方米 C.4416平方米 D.4508平方米
【变式4-3】(2023春 洪洞县期末)如图,将△ABC沿射线BC方向移动,使点B移动到点C,得到△DCE,连接AE,若△ABC的面积为2,则△ACE的面积为( )
A.2 B.4 C.8 D.16
【题型5 利用平移作图】
【例5】(2023春 高邮市期中)如图,在边长为1个单位的正方形网格中,△ABC经过平移后得到△A′B′C′,图中标出了点B的对应点B′.根据下列条件,利用网格点和无刻度的直尺画图并解答相关的问题(保留画图痕迹):
(1)画出△A′B′C′;
(2)连接AA′、CC′,那么AA′与CC′的关系是 ;
(3)△ABC的面积是 .
【变式5-1】(2023春 江都区期中)如图,在方格纸中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点就是小正方形的格点,将△ABC向右平移3个单位长度再向下平移1个单位长度,得到△A′B′C′.
(1)在格中画出平移后的△A′B′C′;
(2)若连接AA′,CC′,则这两段线段的关系是 ;
(3)用直尺作出平移后△A′B′C′高线A′D′;
(4)△ABC的面积是 .
【变式5-2】(2023春 江都区月考)在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,将△ABC先向右平移5格,再向上平移2格得△A1B1C1.
(1)画出平移后的△A1B1C1;
(2)画出△ABC的高BH(借助格点,留下作图痕迹);
(3)图中AC与A1C1的关系是 ;
(4)平移中线段AC扫过部分的面积是 .
【变式5-3】(2023春 兴化市期末)如图,方格纸中每个小正方形的边长都是1,△ABC是格点三角形(三个顶点都在格点上).△ABC经过平移后得到△A'B'C',点B恰好落在点B'处,
(1)请画出平移后的△A'B'C';
(2)△A'B'C'的面积等于 ;
(3)在线段PQ上是否存在格点M,使得△MA'C'的面积是△MA'B'面积的2倍?若存在,请画出所有这样的格点M1,M2,…,若不存在,请说明理由.
【题型6 平移中几何综合问题】
【例6】(2023秋 吉林期末)如图,点C、M、N在射线DQ上,点B在射线AP上,且AP∥DQ,∠D=∠ABC=80°,∠1=∠2,AN平分∠DAM.
(1)试说明AD∥BC的理由;
(2)试求∠CAN的度数;
(3)平移线段BC.
①试问∠AMD:∠ACD的值是否发生变化?若不会,请求出这个比值;若会,请找出相应变化规律;
②若在平移过程中存在某种位置,使得∠AND=∠ACB,试求此时∠ACB的度数.
【变式6-1】(2023春 吉林月考)如图,AM∥BN,线段CD的两个端点C,D分别在射线BN,AM上,且∠A=∠BCD=108°,E是线段AD上一点(不与点A、D重合),BD平分∠EBC.
(1)求∠ABC的度数;
(2)请在图中找出与∠ABC相等的角,并说明理由;
(3)若平行移动CD,那么∠ADB与∠AEB的度数之比是否随着CD位置的变化而发生变化?若变化,找出变化规律;若不变,求出这个比值.
【变式6-2】如图,已知直线AB∥CD,∠A=∠C=100°,E、F在CD上,且满足∠DBF=∠ABD,BE平分∠CBF.
(1)求∠DBE的度数.
(2)若平行移动AD,那么∠BFC:∠BDC的比值是否随之发生变化?若变化,找出变化规律;若不变,求出这个比值.
(3)在平行移动AD的过程中,是否存在某种情况,使∠BEC=∠ADB?若存在,求出其度数;若不存在,请说明理由.
【变式6-3】(2023春 奉化区校级期末)如图,AB∥CD,点C在点D的右侧,∠ABC,∠ADC的平分线交于点E(不与B,D点重合),∠ADC=70°.设∠BED=n°.
(1)若点B在点A的左侧,求∠ABC的度数;(用含n的代数式表示)
(2)将(1)中的线段BC沿DC方向平移,当点B移动到点A右侧时,请画出图形并判断∠ABC的度数是否改变.若改变,请求出∠ABC的度数(用含n的代数式表示);若不变,请说明理由.
图形的平移-重难点题型
【知识点1 平移的定义】
1.图形的平移必须具备两个要素:平移的方向与平移的距离.其中,平移的方向是平移前图形上的某一点到其对应点所指的方向;平移的距离是平移前图形上的某一点到其对应点之间的距离.
2.平移只改变位置,形状与大小都不改变。
【题型1 平移的定义】
【例1】(2023春 扬州期末)下列图形中哪一个图形不能由平移得到( )
A. B. C. D.
【分析】根据平移概念,将图形上的所有点都按照某一个方向做相同距离的移动叫平移,可以直接得出答案.
【解答】解;根据平移的概念;A,B.D,都是平移,只有C是旋转,
故选:C.
【变式1-1】(2023春 临西县期末)下列各组图形可以通过平移互相得到的是( )
A. B.
C. D.
【分析】根据平移不改变图形的形状和大小,将题中所示的图案通过平移后可以得到的图案是C.
【解答】解:观察图形可知图案C通过平移后可以得到.
故选:C.
【变式1-2】(2023春 包河区期末)下列几种运动中属于平移的有( )
①水平运输带上砖的运动;
②笔直的铁路上行驶的动车(忽略车轮的转动);
③升降机上下做机械运动;
④足球场上足球的运动.
A.4种 B.3种 C.2种 D.1种
【分析】根据平移的性质,对各小题进行分析判断即可求解.
【解答】解:①水平运输带上砖的运动,是平移变换;
②笔直的铁路上行驶的动车(忽略车轮的转动),是平移变换;
③升降机上下做机械运动,是平移变换;
④足球场上足球的运动,是旋转运动.
所以属于平移的有①②③共3种.
故选:B.
【变式1-3】(2023春 龙岗区期末)在以下现象中:①用打气筒打气时,气筒里活塞的运动;②传送带上,瓶装饮料的移动;③在笔直的公路上行驶的汽车;④温度计中,液柱的上升或下降;⑤钟摆的摆动.属于平移的是( )
A.① B.①② C.①②③ D.①②③④
【分析】根据平移的性质,对题中的现象进行一一分析,选出正确答案.
【解答】解:①用打气筒打气时,气筒里活塞沿直线运动,符合平移的性质,故属平移;
②传送带上,瓶装饮料的移动沿直线运动,符合平移的性质,故属平移;
③在笔直的公路上行驶的汽车沿直线运动,符合平移的性质,故属平移;
④随温度计中,液柱的上升或下降时,体积要发生变化,不符合平移的性质;
⑤钟摆的摆动,在运动的过程中改变图形的方向,不符合平移的性质.
故选:C.
【知识点2 平移的性质】
(1)平移得到的图形与原图形中的对应线段平行(或在同一条直线上)且相等;对应角相等;对应点的连线平行(或共线)且相等;
(2)“将一个图形沿某一个方向移动一定的距离”意味着“图形上的每一个点都沿同一方向移动了相同的距离”。
【题型2 利用平移的性质解长度问题】
【例2】(2023春 西城区校级期中)如图所示:某公园里有一处长方形风景欣赏区ABCD,AB长50米,BC宽25米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小明同学在假期沿着小路的中间行走(图中虚线),则:小明同学所走的路径长约为( )米.(小路的宽度忽略不计)
A.150米 B.125米 C.100米 D.75米
【分析】由于路的宽度忽略不计,因此行走的路线的长AD+AB+BC,代入计算即可.
【解答】解:由平移的性质可知,由于小路的宽度忽略不计,因此说行走的路程为AD+AB+BC=25+50+25=100(米),
故选:C.
【变式2-1】(2023春 伍家岗区期末)如图是一段台阶的截面图,高BC为5米,直角边AC为12米,现打算在台阶上铺上一整张防滑毯,至少需防滑毯的长为( )
A.12米 B.13米 C.17米 D.18米
【分析】根据平移可知防滑毯的长度等于横向与纵向的长度之和即可求出地毯的长度.
【解答】解:防滑毯的长度为:5+12=17(米);
故选:C.
【变式2-2】(2023春 含山县期末)夏季荷花盛开,为了便于游客领略“人从桥上过,如在河中行”的美好意境,某景点拟在如图所示的长方形荷塘上架设小桥(图中虚线),若荷塘周长为900m,且桥宽忽略不计,则小桥的总长为 450 m.
【分析】根据图形得出荷塘中小桥的总长为矩形的长与宽的和,进而得出答案.
【解答】解:∵荷塘周长为900m,
∴小桥总长为:900÷2=450(m).
故答案为:450.
【变式2-3】(2023春 炎陵县期末)如图,从甲地到乙地有三条路线:①甲→A→D→乙;②甲→B→D→乙;③甲→B→C→乙,在这三条路线中,走哪条路线近?答案是( )
A.① B.①② C.①③ D.①②③
【分析】将三条路线分别平移,可知这三条路线的长度都是长方形周长的一半.
【解答】解:如图所示:
三条路线的长度都等于大长方形周长的一半.
故选:D.
【题型3 利用平移的性质解周长问题】
【例3】(2023秋 市中区期末)如图,三角形ABC中,AB=2cm,AC=3cm,BC=3.5cm,将三角形ABC沿BC方向平移2cm,连接AD,则四边形ACFD的周长是 10cm .
【分析】先利用平移的性质得到AD=CF=2cm,DF=AC=3cm,然后计算四边形ACFD的周长.
【解答】解:∵三角形ABC沿BCA方向平移2cm得到△DEF,
∴AD=CF=2cm,DF=AC=3cm,
∴四边形ACFD的周长=2+3+2+3=10(cm).
故答案为10cm.
【变式3-1】(2023秋 江夏区期中)如图,将△ABC向右平移acm(a>0)得到△DEF,连接AD,若△ABC的周长是36cm,则四边形ABFD的周长是( )
A.(36+a)cm B.(72+a)cm C.(36+2a)cm D.(72+2a)cm
【分析】先根据平移的性质得出AD=a,BF=BC+CF=BC+a,DF=AC,再根据四边形ABFD的周长=AD+AB+BF+DF即可得出结论.
【解答】解:∵将周长为36cm的△ABC沿边BC向右平移a个单位得到△DEF,
∴AD=a,BF=BC+CF=BC+a,DF=AC,
又∵AB+BC+AC=36cm,
∴四边形ABFD的周长=AD+AB+BF+DF=a+AB+BC+a+AC=(36+2a)(cm).
故选:C.
【变式3-2】(2023春 庐江县期中)如图,将△ABC沿CB向左平移3cm得到△DEF,AB,DF相交于点G,如果△ABC的周长是12cm,那么△ADG与△GBF周长之和为( )
A.12cm B.15cm C.18cm D.24cm
【分析】根据平移的性质可得AD=EB,然后判断出△ADG与△BGF的周长之和=AD+DG+GF+AG+BG+BF=EF+AB+DF,然后代入数据计算即可得解.
【解答】解:∵将△ABC向左平移3cm得到△DEF,
∴AD=EB,
∴△ADG与△GBF的周长之和=AD+DG+GF+AG+BG+BF=EF+AB+DF=BC+AB+AC=12(cm),
故选:A.
【变式3-3】(2023 宁波模拟)如图,所有角均为直角,所有线段均不相等,若要知道该图形周长,至少需要知道几条线段的长( )
A.3条 B.4条 C.5条 D.6条
【分析】根据题意,结合图形,通过平移构成矩形,据此判断即可.
【解答】解:如图:
若要知道该图形周长,至少需要知道4条线段的长:BC、AB,IJ,EF,
∵BC=AL+KJ+IH+GF+DE,AB=LK+KK′=LK+CC′,IJ=HG+GG′=HG+C′D′,EF=DD′,
∴只要知道BC、AB,IJ,EF4条线段的长,就能知道该图形周长.
故选:B.
【题型4 利用平移的性质解面积问题】
【例4】(2023秋 海阳市期末)如图,将Rt△ABC沿着点B到点C的方向平移到△DEF的位置,已知AB=6,HD=2,CF=3,则图中阴影部分的面积为( )
A.12 B.15 C.18 D.24
【分析】先判断出阴影部分面积等于梯形ABEH的面积,再根据平移变化只改变图形的位置不改变图形的形状可得DE=AB,然后求出HE,根据平移的距离求出BE=CF=3,然后利用梯形的面积公式列式计算即可得解.
【解答】解:∵△ABC沿着点B到点C的方向平移到△DEF的位置,
∴△ABC的面积=△DEF的面积,
∴阴影部分面积等于梯形ABEH的面积,
由平移的性质得,DE=AB=6,BE=CF=3,
∵AB=6,DH=2,
∴HE=DE﹣DH=6﹣2=4,
∴阴影部分的面积(4+6)×3=15.
故选:B.
【变式4-1】(2023春 市中区期末)如图,在△ABC中,∠B=90°,AB=10.将△ABC沿着BC的方向平移至△DEF,若平移的距离是5,则图中阴影部分的面积为( )
A.25 B.50 C.35 D.70
【分析】先根据平移的性质得AC=DF,AD=CF=5,于是可判断四边形ACFD为平行四边形,然后根据平行四边形的面积公式计算即可.
【解答】解:∵直角△ABC沿BC边平移5个单位得到直角△DEF,
∴AC=DF,AD=CF=5,
∴四边形ACFD为平行四边形,
∴S平行四边形ACFD=CF AB=5×10=50,
即阴影部分的面积为50,
故选:B.
【变式4-2】(2023春 和平区校级月考)如图,一块形状为长方形ABCD的场地,长AB=98米,宽AD=46米,A、B两处入口E小路宽都为1米,两小路汇合处路口宽2米,其余部分种植草坪,那么草坪的面积为( )
A.4320平方米 B.4410平方米 C.4416平方米 D.4508平方米
【分析】本题要看图解答.从图中可以看出剩余部分的草坪正好可以拼成一个长方形,然后根据题意求出长和宽,最后可求出面积.
【解答】解:由图可知:矩形ABCD中去掉小路后,草坪正好可以拼成一个新的矩形,
且它的长为:98﹣2=96,宽为46﹣1=45,
所以草坪的面积是:长×宽=96×45=4320(米2).
故选:A.
【变式4-3】(2023春 洪洞县期末)如图,将△ABC沿射线BC方向移动,使点B移动到点C,得到△DCE,连接AE,若△ABC的面积为2,则△ACE的面积为( )
A.2 B.4 C.8 D.16
【分析】首先根据平移的性质,可得BC=CE;然后根据两个三角形的高相等时,面积和底成正比,可得△ACE的面积等于△ABC的面积,据此解答即可.
【解答】解:∵将△ABC沿射线BC方向移动,使点B移动到点C,得到△DCE,
∴BC=CE,
∵△ACE和△ABC底边和高都相等,
∴△ACE的面积等于△ABC的面积,
又∵△ABC的面积为2,
∴△ACE的面积为2.
故选:A.
【题型5 利用平移作图】
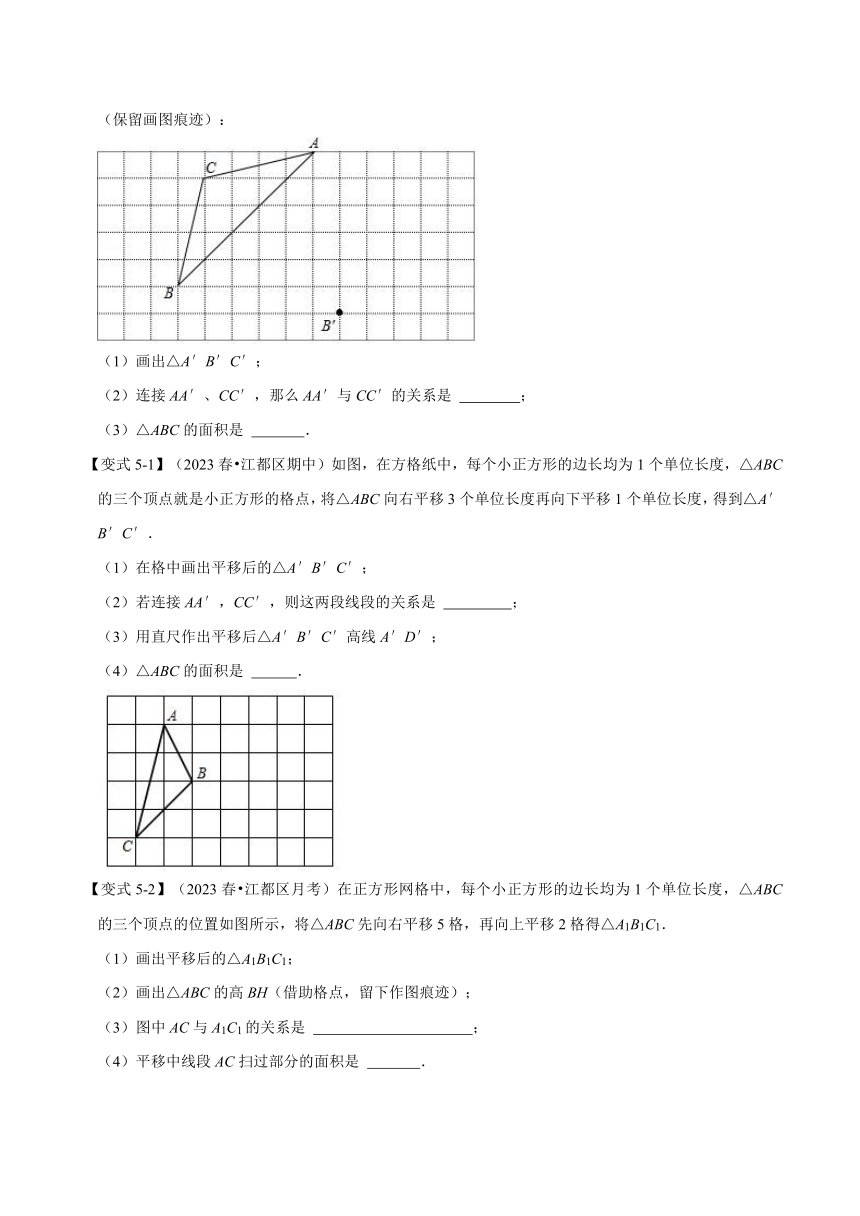
【例5】(2023春 高邮市期中)如图,在边长为1个单位的正方形网格中,△ABC经过平移后得到△A′B′C′,图中标出了点B的对应点B′.根据下列条件,利用网格点和无刻度的直尺画图并解答相关的问题(保留画图痕迹):
(1)画出△A′B′C′;
(2)连接AA′、CC′,那么AA′与CC′的关系是 平行且相等 ;
(3)△ABC的面积是 7.5 .
【分析】(1)利用网格特点和平移的性质,画出A、B、C的对应点即可;
(2)根据平移的性质进行判断;
(3)用一个矩形的面积分别减去三个直角三角形的面积和一个小正方形的面积去计算△ABC的面积.
【解答】解:(1)如图,△A′B′C′为所求;
(2)如图,AA′=CC′,AA′∥CC′;
故答案为平行且相等;
(3)△ABC的面积=5×54×14×1﹣15×5=7.5.
故答案为7.5.
【变式5-1】(2023春 江都区期中)如图,在方格纸中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点就是小正方形的格点,将△ABC向右平移3个单位长度再向下平移1个单位长度,得到△A′B′C′.
(1)在格中画出平移后的△A′B′C′;
(2)若连接AA′,CC′,则这两段线段的关系是 平行且相等. ;
(3)用直尺作出平移后△A′B′C′高线A′D′;
(4)△ABC的面积是 3 .
【分析】(1)利用平移变换的性质分别作出A,B,C的对应点A′,B′,C′即可.
(2)利用平移变换的性质判断即可.
(3)根据三角形的高的定义作出图形即可.
(4)利用分割法把三角形面积看成矩形面积截取周围三个三角形面积即可.
【解答】解:(1)如图,△A′B′C′即为所求.
(2)如图,AA′∥CC′.
故答案为:平行且相等.
(3)如图,线段A′D′即为所求.
(4)△ABC的面积=2×41×41×22×2=3,
故答案为:3.
【变式5-2】(2023春 江都区月考)在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,将△ABC先向右平移5格,再向上平移2格得△A1B1C1.
(1)画出平移后的△A1B1C1;
(2)画出△ABC的高BH(借助格点,留下作图痕迹);
(3)图中AC与A1C1的关系是 AC=A1C1,AC∥A1C1 ;
(4)平移中线段AC扫过部分的面积是 28 .
【分析】(1)利用平移变换的性质分别作出A,B,C的对应点A1,B1,C1即可.
(2)根据三角形的高的定义,画出图形即可.
(3)利用平移变换的性质判断即可.
(4)平移中线段AC扫过部分的面积是两个平行四边形的面积之和.
【解答】解:(1)如图,△A1B1C1即为所求.
(2)如图,线段BH即为所求.
(3)图中AC与A1C1的关系是AC=A1C1,AC∥A1C1.
故答案为:AC=A1C1,AC∥A1C1.
(4)平移中线段AC扫过部分的面积是 5×4+2×4=28.
【变式5-3】(2023春 兴化市期末)如图,方格纸中每个小正方形的边长都是1,△ABC是格点三角形(三个顶点都在格点上).△ABC经过平移后得到△A'B'C',点B恰好落在点B'处,
(1)请画出平移后的△A'B'C';
(2)△A'B'C'的面积等于 ;
(3)在线段PQ上是否存在格点M,使得△MA'C'的面积是△MA'B'面积的2倍?若存在,请画出所有这样的格点M1,M2,…,若不存在,请说明理由.
【分析】(1)将三个顶点分别向左平移5个单位、向上平移2个单位得到其对应点,再首尾顺次连接即可;
(2)利用割补法,用长为2、宽为6的矩形面积减去四周的三个三角形的面积即可;
(3)根据三个三角形的高相同,要使△MA'C'的面积是△MA'B'面积的2倍只需使对应底边的长度满足2倍的关系即可.
【解答】解:(1)画出平移后的△A'B'C';
(2)△A'B'C'的面积等于3×63×32×31×6,
故答案为:;
(3)如图所示,点M1、M2即为所求.
【题型6 平移中几何综合问题】
【例6】(2023秋 吉林期末)如图,点C、M、N在射线DQ上,点B在射线AP上,且AP∥DQ,∠D=∠ABC=80°,∠1=∠2,AN平分∠DAM.
(1)试说明AD∥BC的理由;
(2)试求∠CAN的度数;
(3)平移线段BC.
①试问∠AMD:∠ACD的值是否发生变化?若不会,请求出这个比值;若会,请找出相应变化规律;
②若在平移过程中存在某种位置,使得∠AND=∠ACB,试求此时∠ACB的度数.
【分析】(1)根据平行线的性质和判定解答即可;
(2)根据角平分线的定义解答即可;
(3)根据平移的性质和平行线的性质解答即可.
【解答】解:(1)∵AP∥DQ,
∴∠D+∠DAB=180°.
∵∠D=80°,
∴∠DAB=100°.
∵∠ABC=80°,
∴∠DAB+∠ABC=180°,
∴AD∥BC;
(2)∵AN平分∠DAM,
∴∠NAM=∠NAD∠DAM.
∵∠1=∠2,
∴∠CAM∠BAM.
∴∠NAM+∠CAM∠DAM∠BAM,
即:∠CAN∠DAB
∵∠DAB=100°,
∴∠CAN=50°,
(3)①不会.
∵AP∥DQ,
∴∠AMD=∠MAB=2∠1,∠ACD=∠1,
∴∠AMD:∠ACD=2,
②∵AP∥DQ,AD∥BC,
∴∠AND=∠NAB,∠ACB=∠DAC,
∵∠AND=∠ACB,
∴∠NAB=∠DAC,
∴∠NAB﹣∠NAC=∠DAC﹣∠NAC,
即:∠1=∠DAN.
∴∠1=∠2=∠DAN=∠MAN=25°,
∴∠ACB=∠DAC=75°.
【变式6-1】(2023春 吉林月考)如图,AM∥BN,线段CD的两个端点C,D分别在射线BN,AM上,且∠A=∠BCD=108°,E是线段AD上一点(不与点A、D重合),BD平分∠EBC.
(1)求∠ABC的度数;
(2)请在图中找出与∠ABC相等的角,并说明理由;
(3)若平行移动CD,那么∠ADB与∠AEB的度数之比是否随着CD位置的变化而发生变化?若变化,找出变化规律;若不变,求出这个比值.
【分析】(1)由“两直线平行,同旁内角互补”求得∠ABC的度数;
(2)与∠ABC相等的角:∠ADC,∠DCN.根据平行线的性质进行证明即可;
(3)由平行线的性质和角平分线的定义推知.
【解答】解:(1)∵AM∥BN,
∴∠A+∠ABC=180°,
∴∠ABC=180°﹣∠A=180108°=72°;
(2)与∠ABC相等的角:∠ADC,∠DCN.
理由:∵AM∥BN,
∠ADC=∠DCN,∠ADC+∠BCD=180°,
∴∠ADC=180°﹣∠BCD=72°,
∴∠DCN=72°,
∴∠ADC=∠DCN=∠ABC;
(3)不发生变化.
∵AM∥BN,
∴∠AEB=∠EBC,∠ADB=∠DBC.
∵BD平分∠EBC,
∴∠DBC∠EBC,
∴∠ADB∠AEB,
∴.
【变式6-2】如图,已知直线AB∥CD,∠A=∠C=100°,E、F在CD上,且满足∠DBF=∠ABD,BE平分∠CBF.
(1)求∠DBE的度数.
(2)若平行移动AD,那么∠BFC:∠BDC的比值是否随之发生变化?若变化,找出变化规律;若不变,求出这个比值.
(3)在平行移动AD的过程中,是否存在某种情况,使∠BEC=∠ADB?若存在,求出其度数;若不存在,请说明理由.
【分析】(1)由直线AB∥CD,根据两直线平行,同旁内角互补,即可求得∠ABC的度数,又由∠DBE∠ABC,即可求得∠DBE的度数.
(2)由直线AB∥CD,根据两直线平行,内错角相等,即可求得∠BFC=∠ABF=2∠ABD,∠ABD=∠BDC,继而可求得∠BFC:∠BDC的比值;
(3)首先设∠ABD=∠DBF=∠BDC=x°,由直线AB∥CD,根据两直线平行,同旁内角互补与两直线平行,内错角相等,可求得∠BEC与∠ADB的度数,又由∠BEC=∠ADB,即可得方程:x°+40°=80°﹣x°,解此方程即可求得答案.
【解答】解:(1)∵AB∥CD,
∴∠ABC=180°﹣∠C=80°,
∵∠DBF=∠ABD,BE平分∠CBF,
∴∠DBE∠ABF∠CBF∠ABC=40°;
(2)不变.
理由∵AB∥CD,
∴∠BFC=∠ABF=2∠ABD,∠ABD=∠BDC,
∴∠BFC=2∠BDC,
∴∠BFC:∠BDC=2:1;
(3)存在.
设∠ABD=∠DBF=∠BDC=x°.
∵AB∥CD,
∴∠BEC=∠ABE=x°+40°;
∵AB∥CD,
∴∠ADC=180°﹣∠A=80°,
∴∠ADB=80°﹣x°.
若∠BEC=∠ADB,
则x°+40°=80°﹣x°,
得x°=20°.
∴存在∠BEC=∠ADB=60°.
【变式6-3】(2023春 奉化区校级期末)如图,AB∥CD,点C在点D的右侧,∠ABC,∠ADC的平分线交于点E(不与B,D点重合),∠ADC=70°.设∠BED=n°.
(1)若点B在点A的左侧,求∠ABC的度数;(用含n的代数式表示)
(2)将(1)中的线段BC沿DC方向平移,当点B移动到点A右侧时,请画出图形并判断∠ABC的度数是否改变.若改变,请求出∠ABC的度数(用含n的代数式表示);若不变,请说明理由.
【分析】根据平行线的性质即可求解.
【解答】解:(1)如图1,过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠ABE=∠BEF,∠CDE=∠DEF,
∵BE平分∠ABC,DE平分∠ADC,∠ADC=70°,
∴∠ABC=2∠ABE=2∠BEF,,
∵∠BED=n°,
∴∠BEF=(n﹣35)°,
∴∠ABC=2∠BEF=2(n﹣35)°=(2n﹣70)°;
(2)∠ABC的度数改变,
画出的图形如图2,过点E作EF∥AB,
∵BE平分∠ABC,DE平分∠ADC,∠ADC=70°,
∴∠ABC=2∠ABE,,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠ABE+∠BEF=180°,∠CDE=∠DEF=35°,
∵∠BED=n°,
∴∠BEF=(n﹣35)°,
∴∠ABE=180°﹣∠BEF=180°﹣(n﹣35)°=180°﹣n°+35°=(215﹣n)°,
∴∠ABC=2∠ABE=2(215﹣n)°=(430﹣2n)°.
【知识点1 平移的定义】
1.图形的平移必须具备两个要素:平移的方向与平移的距离.其中,平移的方向是平移前图形上的某一点到其对应点所指的方向;平移的距离是平移前图形上的某一点到其对应点之间的距离.
2.平移只改变位置,形状与大小都不改变。
【题型1 平移的定义】
【例1】(2023春 扬州期末)下列图形中哪一个图形不能由平移得到( )
A. B. C. D.
【变式1-1】(2023春 临西县期末)下列各组图形可以通过平移互相得到的是( )
A. B.
C. D.
【变式1-2】(2023春 包河区期末)下列几种运动中属于平移的有( )
①水平运输带上砖的运动;
②笔直的铁路上行驶的动车(忽略车轮的转动);
③升降机上下做机械运动;
④足球场上足球的运动.
A.4种 B.3种 C.2种 D.1种
【变式1-3】(2023春 龙岗区期末)在以下现象中:①用打气筒打气时,气筒里活塞的运动;②传送带上,瓶装饮料的移动;③在笔直的公路上行驶的汽车;④温度计中,液柱的上升或下降;⑤钟摆的摆动.属于平移的是( )
A.① B.①② C.①②③ D.①②③④
【知识点2 平移的性质】
(1)平移得到的图形与原图形中的对应线段平行(或在同一条直线上)且相等;对应角相等;对应点的连线平行(或共线)且相等;
(2)“将一个图形沿某一个方向移动一定的距离”意味着“图形上的每一个点都沿同一方向移动了相同的距离”。
【题型2 利用平移的性质解长度问题】
【例2】(2023春 西城区校级期中)如图所示:某公园里有一处长方形风景欣赏区ABCD,AB长50米,BC宽25米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小明同学在假期沿着小路的中间行走(图中虚线),则:小明同学所走的路径长约为( )米.(小路的宽度忽略不计)
A.150米 B.125米 C.100米 D.75米
【变式2-1】(2023春 伍家岗区期末)如图是一段台阶的截面图,高BC为5米,直角边AC为12米,现打算在台阶上铺上一整张防滑毯,至少需防滑毯的长为( )
A.12米 B.13米 C.17米 D.18米
【变式2-2】(2023春 含山县期末)夏季荷花盛开,为了便于游客领略“人从桥上过,如在河中行”的美好意境,某景点拟在如图所示的长方形荷塘上架设小桥(图中虚线),若荷塘周长为900m,且桥宽忽略不计,则小桥的总长为 m.
【变式2-3】(2023春 炎陵县期末)如图,从甲地到乙地有三条路线:①甲→A→D→乙;②甲→B→D→乙;③甲→B→C→乙,在这三条路线中,走哪条路线近?答案是( )
A.① B.①② C.①③ D.①②③
【题型3 利用平移的性质解周长问题】
【例3】(2023秋 市中区期末)如图,三角形ABC中,AB=2cm,AC=3cm,BC=3.5cm,将三角形ABC沿BC方向平移2cm,连接AD,则四边形ACFD的周长是 .
【变式3-1】(2023秋 江夏区期中)如图,将△ABC向右平移acm(a>0)得到△DEF,连接AD,若△ABC的周长是36cm,则四边形ABFD的周长是( )
A.(36+a)cm B.(72+a)cm C.(36+2a)cm D.(72+2a)cm
【变式3-2】(2023春 庐江县期中)如图,将△ABC沿CB向左平移3cm得到△DEF,AB,DF相交于点G,如果△ABC的周长是12cm,那么△ADG与△GBF周长之和为( )
A.12cm B.15cm C.18cm D.24cm
【变式3-3】(2023 宁波模拟)如图,所有角均为直角,所有线段均不相等,若要知道该图形周长,至少需要知道几条线段的长( )
A.3条 B.4条 C.5条 D.6条
【题型4 利用平移的性质解面积问题】
【例4】(2023秋 海阳市期末)如图,将Rt△ABC沿着点B到点C的方向平移到△DEF的位置,已知AB=6,HD=2,CF=3,则图中阴影部分的面积为( )
A.12 B.15 C.18 D.24
【变式4-1】(2023春 市中区期末)如图,在△ABC中,∠B=90°,AB=10.将△ABC沿着BC的方向平移至△DEF,若平移的距离是5,则图中阴影部分的面积为( )
A.25 B.50 C.35 D.70
【变式4-2】(2023春 和平区校级月考)如图,一块形状为长方形ABCD的场地,长AB=98米,宽AD=46米,A、B两处入口E小路宽都为1米,两小路汇合处路口宽2米,其余部分种植草坪,那么草坪的面积为( )
A.4320平方米 B.4410平方米 C.4416平方米 D.4508平方米
【变式4-3】(2023春 洪洞县期末)如图,将△ABC沿射线BC方向移动,使点B移动到点C,得到△DCE,连接AE,若△ABC的面积为2,则△ACE的面积为( )
A.2 B.4 C.8 D.16
【题型5 利用平移作图】
【例5】(2023春 高邮市期中)如图,在边长为1个单位的正方形网格中,△ABC经过平移后得到△A′B′C′,图中标出了点B的对应点B′.根据下列条件,利用网格点和无刻度的直尺画图并解答相关的问题(保留画图痕迹):
(1)画出△A′B′C′;
(2)连接AA′、CC′,那么AA′与CC′的关系是 ;
(3)△ABC的面积是 .
【变式5-1】(2023春 江都区期中)如图,在方格纸中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点就是小正方形的格点,将△ABC向右平移3个单位长度再向下平移1个单位长度,得到△A′B′C′.
(1)在格中画出平移后的△A′B′C′;
(2)若连接AA′,CC′,则这两段线段的关系是 ;
(3)用直尺作出平移后△A′B′C′高线A′D′;
(4)△ABC的面积是 .
【变式5-2】(2023春 江都区月考)在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,将△ABC先向右平移5格,再向上平移2格得△A1B1C1.
(1)画出平移后的△A1B1C1;
(2)画出△ABC的高BH(借助格点,留下作图痕迹);
(3)图中AC与A1C1的关系是 ;
(4)平移中线段AC扫过部分的面积是 .
【变式5-3】(2023春 兴化市期末)如图,方格纸中每个小正方形的边长都是1,△ABC是格点三角形(三个顶点都在格点上).△ABC经过平移后得到△A'B'C',点B恰好落在点B'处,
(1)请画出平移后的△A'B'C';
(2)△A'B'C'的面积等于 ;
(3)在线段PQ上是否存在格点M,使得△MA'C'的面积是△MA'B'面积的2倍?若存在,请画出所有这样的格点M1,M2,…,若不存在,请说明理由.
【题型6 平移中几何综合问题】
【例6】(2023秋 吉林期末)如图,点C、M、N在射线DQ上,点B在射线AP上,且AP∥DQ,∠D=∠ABC=80°,∠1=∠2,AN平分∠DAM.
(1)试说明AD∥BC的理由;
(2)试求∠CAN的度数;
(3)平移线段BC.
①试问∠AMD:∠ACD的值是否发生变化?若不会,请求出这个比值;若会,请找出相应变化规律;
②若在平移过程中存在某种位置,使得∠AND=∠ACB,试求此时∠ACB的度数.
【变式6-1】(2023春 吉林月考)如图,AM∥BN,线段CD的两个端点C,D分别在射线BN,AM上,且∠A=∠BCD=108°,E是线段AD上一点(不与点A、D重合),BD平分∠EBC.
(1)求∠ABC的度数;
(2)请在图中找出与∠ABC相等的角,并说明理由;
(3)若平行移动CD,那么∠ADB与∠AEB的度数之比是否随着CD位置的变化而发生变化?若变化,找出变化规律;若不变,求出这个比值.
【变式6-2】如图,已知直线AB∥CD,∠A=∠C=100°,E、F在CD上,且满足∠DBF=∠ABD,BE平分∠CBF.
(1)求∠DBE的度数.
(2)若平行移动AD,那么∠BFC:∠BDC的比值是否随之发生变化?若变化,找出变化规律;若不变,求出这个比值.
(3)在平行移动AD的过程中,是否存在某种情况,使∠BEC=∠ADB?若存在,求出其度数;若不存在,请说明理由.
【变式6-3】(2023春 奉化区校级期末)如图,AB∥CD,点C在点D的右侧,∠ABC,∠ADC的平分线交于点E(不与B,D点重合),∠ADC=70°.设∠BED=n°.
(1)若点B在点A的左侧,求∠ABC的度数;(用含n的代数式表示)
(2)将(1)中的线段BC沿DC方向平移,当点B移动到点A右侧时,请画出图形并判断∠ABC的度数是否改变.若改变,请求出∠ABC的度数(用含n的代数式表示);若不变,请说明理由.
图形的平移-重难点题型
【知识点1 平移的定义】
1.图形的平移必须具备两个要素:平移的方向与平移的距离.其中,平移的方向是平移前图形上的某一点到其对应点所指的方向;平移的距离是平移前图形上的某一点到其对应点之间的距离.
2.平移只改变位置,形状与大小都不改变。
【题型1 平移的定义】
【例1】(2023春 扬州期末)下列图形中哪一个图形不能由平移得到( )
A. B. C. D.
【分析】根据平移概念,将图形上的所有点都按照某一个方向做相同距离的移动叫平移,可以直接得出答案.
【解答】解;根据平移的概念;A,B.D,都是平移,只有C是旋转,
故选:C.
【变式1-1】(2023春 临西县期末)下列各组图形可以通过平移互相得到的是( )
A. B.
C. D.
【分析】根据平移不改变图形的形状和大小,将题中所示的图案通过平移后可以得到的图案是C.
【解答】解:观察图形可知图案C通过平移后可以得到.
故选:C.
【变式1-2】(2023春 包河区期末)下列几种运动中属于平移的有( )
①水平运输带上砖的运动;
②笔直的铁路上行驶的动车(忽略车轮的转动);
③升降机上下做机械运动;
④足球场上足球的运动.
A.4种 B.3种 C.2种 D.1种
【分析】根据平移的性质,对各小题进行分析判断即可求解.
【解答】解:①水平运输带上砖的运动,是平移变换;
②笔直的铁路上行驶的动车(忽略车轮的转动),是平移变换;
③升降机上下做机械运动,是平移变换;
④足球场上足球的运动,是旋转运动.
所以属于平移的有①②③共3种.
故选:B.
【变式1-3】(2023春 龙岗区期末)在以下现象中:①用打气筒打气时,气筒里活塞的运动;②传送带上,瓶装饮料的移动;③在笔直的公路上行驶的汽车;④温度计中,液柱的上升或下降;⑤钟摆的摆动.属于平移的是( )
A.① B.①② C.①②③ D.①②③④
【分析】根据平移的性质,对题中的现象进行一一分析,选出正确答案.
【解答】解:①用打气筒打气时,气筒里活塞沿直线运动,符合平移的性质,故属平移;
②传送带上,瓶装饮料的移动沿直线运动,符合平移的性质,故属平移;
③在笔直的公路上行驶的汽车沿直线运动,符合平移的性质,故属平移;
④随温度计中,液柱的上升或下降时,体积要发生变化,不符合平移的性质;
⑤钟摆的摆动,在运动的过程中改变图形的方向,不符合平移的性质.
故选:C.
【知识点2 平移的性质】
(1)平移得到的图形与原图形中的对应线段平行(或在同一条直线上)且相等;对应角相等;对应点的连线平行(或共线)且相等;
(2)“将一个图形沿某一个方向移动一定的距离”意味着“图形上的每一个点都沿同一方向移动了相同的距离”。
【题型2 利用平移的性质解长度问题】
【例2】(2023春 西城区校级期中)如图所示:某公园里有一处长方形风景欣赏区ABCD,AB长50米,BC宽25米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小明同学在假期沿着小路的中间行走(图中虚线),则:小明同学所走的路径长约为( )米.(小路的宽度忽略不计)
A.150米 B.125米 C.100米 D.75米
【分析】由于路的宽度忽略不计,因此行走的路线的长AD+AB+BC,代入计算即可.
【解答】解:由平移的性质可知,由于小路的宽度忽略不计,因此说行走的路程为AD+AB+BC=25+50+25=100(米),
故选:C.
【变式2-1】(2023春 伍家岗区期末)如图是一段台阶的截面图,高BC为5米,直角边AC为12米,现打算在台阶上铺上一整张防滑毯,至少需防滑毯的长为( )
A.12米 B.13米 C.17米 D.18米
【分析】根据平移可知防滑毯的长度等于横向与纵向的长度之和即可求出地毯的长度.
【解答】解:防滑毯的长度为:5+12=17(米);
故选:C.
【变式2-2】(2023春 含山县期末)夏季荷花盛开,为了便于游客领略“人从桥上过,如在河中行”的美好意境,某景点拟在如图所示的长方形荷塘上架设小桥(图中虚线),若荷塘周长为900m,且桥宽忽略不计,则小桥的总长为 450 m.
【分析】根据图形得出荷塘中小桥的总长为矩形的长与宽的和,进而得出答案.
【解答】解:∵荷塘周长为900m,
∴小桥总长为:900÷2=450(m).
故答案为:450.
【变式2-3】(2023春 炎陵县期末)如图,从甲地到乙地有三条路线:①甲→A→D→乙;②甲→B→D→乙;③甲→B→C→乙,在这三条路线中,走哪条路线近?答案是( )
A.① B.①② C.①③ D.①②③
【分析】将三条路线分别平移,可知这三条路线的长度都是长方形周长的一半.
【解答】解:如图所示:
三条路线的长度都等于大长方形周长的一半.
故选:D.
【题型3 利用平移的性质解周长问题】
【例3】(2023秋 市中区期末)如图,三角形ABC中,AB=2cm,AC=3cm,BC=3.5cm,将三角形ABC沿BC方向平移2cm,连接AD,则四边形ACFD的周长是 10cm .
【分析】先利用平移的性质得到AD=CF=2cm,DF=AC=3cm,然后计算四边形ACFD的周长.
【解答】解:∵三角形ABC沿BCA方向平移2cm得到△DEF,
∴AD=CF=2cm,DF=AC=3cm,
∴四边形ACFD的周长=2+3+2+3=10(cm).
故答案为10cm.
【变式3-1】(2023秋 江夏区期中)如图,将△ABC向右平移acm(a>0)得到△DEF,连接AD,若△ABC的周长是36cm,则四边形ABFD的周长是( )
A.(36+a)cm B.(72+a)cm C.(36+2a)cm D.(72+2a)cm
【分析】先根据平移的性质得出AD=a,BF=BC+CF=BC+a,DF=AC,再根据四边形ABFD的周长=AD+AB+BF+DF即可得出结论.
【解答】解:∵将周长为36cm的△ABC沿边BC向右平移a个单位得到△DEF,
∴AD=a,BF=BC+CF=BC+a,DF=AC,
又∵AB+BC+AC=36cm,
∴四边形ABFD的周长=AD+AB+BF+DF=a+AB+BC+a+AC=(36+2a)(cm).
故选:C.
【变式3-2】(2023春 庐江县期中)如图,将△ABC沿CB向左平移3cm得到△DEF,AB,DF相交于点G,如果△ABC的周长是12cm,那么△ADG与△GBF周长之和为( )
A.12cm B.15cm C.18cm D.24cm
【分析】根据平移的性质可得AD=EB,然后判断出△ADG与△BGF的周长之和=AD+DG+GF+AG+BG+BF=EF+AB+DF,然后代入数据计算即可得解.
【解答】解:∵将△ABC向左平移3cm得到△DEF,
∴AD=EB,
∴△ADG与△GBF的周长之和=AD+DG+GF+AG+BG+BF=EF+AB+DF=BC+AB+AC=12(cm),
故选:A.
【变式3-3】(2023 宁波模拟)如图,所有角均为直角,所有线段均不相等,若要知道该图形周长,至少需要知道几条线段的长( )
A.3条 B.4条 C.5条 D.6条
【分析】根据题意,结合图形,通过平移构成矩形,据此判断即可.
【解答】解:如图:
若要知道该图形周长,至少需要知道4条线段的长:BC、AB,IJ,EF,
∵BC=AL+KJ+IH+GF+DE,AB=LK+KK′=LK+CC′,IJ=HG+GG′=HG+C′D′,EF=DD′,
∴只要知道BC、AB,IJ,EF4条线段的长,就能知道该图形周长.
故选:B.
【题型4 利用平移的性质解面积问题】
【例4】(2023秋 海阳市期末)如图,将Rt△ABC沿着点B到点C的方向平移到△DEF的位置,已知AB=6,HD=2,CF=3,则图中阴影部分的面积为( )
A.12 B.15 C.18 D.24
【分析】先判断出阴影部分面积等于梯形ABEH的面积,再根据平移变化只改变图形的位置不改变图形的形状可得DE=AB,然后求出HE,根据平移的距离求出BE=CF=3,然后利用梯形的面积公式列式计算即可得解.
【解答】解:∵△ABC沿着点B到点C的方向平移到△DEF的位置,
∴△ABC的面积=△DEF的面积,
∴阴影部分面积等于梯形ABEH的面积,
由平移的性质得,DE=AB=6,BE=CF=3,
∵AB=6,DH=2,
∴HE=DE﹣DH=6﹣2=4,
∴阴影部分的面积(4+6)×3=15.
故选:B.
【变式4-1】(2023春 市中区期末)如图,在△ABC中,∠B=90°,AB=10.将△ABC沿着BC的方向平移至△DEF,若平移的距离是5,则图中阴影部分的面积为( )
A.25 B.50 C.35 D.70
【分析】先根据平移的性质得AC=DF,AD=CF=5,于是可判断四边形ACFD为平行四边形,然后根据平行四边形的面积公式计算即可.
【解答】解:∵直角△ABC沿BC边平移5个单位得到直角△DEF,
∴AC=DF,AD=CF=5,
∴四边形ACFD为平行四边形,
∴S平行四边形ACFD=CF AB=5×10=50,
即阴影部分的面积为50,
故选:B.
【变式4-2】(2023春 和平区校级月考)如图,一块形状为长方形ABCD的场地,长AB=98米,宽AD=46米,A、B两处入口E小路宽都为1米,两小路汇合处路口宽2米,其余部分种植草坪,那么草坪的面积为( )
A.4320平方米 B.4410平方米 C.4416平方米 D.4508平方米
【分析】本题要看图解答.从图中可以看出剩余部分的草坪正好可以拼成一个长方形,然后根据题意求出长和宽,最后可求出面积.
【解答】解:由图可知:矩形ABCD中去掉小路后,草坪正好可以拼成一个新的矩形,
且它的长为:98﹣2=96,宽为46﹣1=45,
所以草坪的面积是:长×宽=96×45=4320(米2).
故选:A.
【变式4-3】(2023春 洪洞县期末)如图,将△ABC沿射线BC方向移动,使点B移动到点C,得到△DCE,连接AE,若△ABC的面积为2,则△ACE的面积为( )
A.2 B.4 C.8 D.16
【分析】首先根据平移的性质,可得BC=CE;然后根据两个三角形的高相等时,面积和底成正比,可得△ACE的面积等于△ABC的面积,据此解答即可.
【解答】解:∵将△ABC沿射线BC方向移动,使点B移动到点C,得到△DCE,
∴BC=CE,
∵△ACE和△ABC底边和高都相等,
∴△ACE的面积等于△ABC的面积,
又∵△ABC的面积为2,
∴△ACE的面积为2.
故选:A.
【题型5 利用平移作图】
【例5】(2023春 高邮市期中)如图,在边长为1个单位的正方形网格中,△ABC经过平移后得到△A′B′C′,图中标出了点B的对应点B′.根据下列条件,利用网格点和无刻度的直尺画图并解答相关的问题(保留画图痕迹):
(1)画出△A′B′C′;
(2)连接AA′、CC′,那么AA′与CC′的关系是 平行且相等 ;
(3)△ABC的面积是 7.5 .
【分析】(1)利用网格特点和平移的性质,画出A、B、C的对应点即可;
(2)根据平移的性质进行判断;
(3)用一个矩形的面积分别减去三个直角三角形的面积和一个小正方形的面积去计算△ABC的面积.
【解答】解:(1)如图,△A′B′C′为所求;
(2)如图,AA′=CC′,AA′∥CC′;
故答案为平行且相等;
(3)△ABC的面积=5×54×14×1﹣15×5=7.5.
故答案为7.5.
【变式5-1】(2023春 江都区期中)如图,在方格纸中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点就是小正方形的格点,将△ABC向右平移3个单位长度再向下平移1个单位长度,得到△A′B′C′.
(1)在格中画出平移后的△A′B′C′;
(2)若连接AA′,CC′,则这两段线段的关系是 平行且相等. ;
(3)用直尺作出平移后△A′B′C′高线A′D′;
(4)△ABC的面积是 3 .
【分析】(1)利用平移变换的性质分别作出A,B,C的对应点A′,B′,C′即可.
(2)利用平移变换的性质判断即可.
(3)根据三角形的高的定义作出图形即可.
(4)利用分割法把三角形面积看成矩形面积截取周围三个三角形面积即可.
【解答】解:(1)如图,△A′B′C′即为所求.
(2)如图,AA′∥CC′.
故答案为:平行且相等.
(3)如图,线段A′D′即为所求.
(4)△ABC的面积=2×41×41×22×2=3,
故答案为:3.
【变式5-2】(2023春 江都区月考)在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,将△ABC先向右平移5格,再向上平移2格得△A1B1C1.
(1)画出平移后的△A1B1C1;
(2)画出△ABC的高BH(借助格点,留下作图痕迹);
(3)图中AC与A1C1的关系是 AC=A1C1,AC∥A1C1 ;
(4)平移中线段AC扫过部分的面积是 28 .
【分析】(1)利用平移变换的性质分别作出A,B,C的对应点A1,B1,C1即可.
(2)根据三角形的高的定义,画出图形即可.
(3)利用平移变换的性质判断即可.
(4)平移中线段AC扫过部分的面积是两个平行四边形的面积之和.
【解答】解:(1)如图,△A1B1C1即为所求.
(2)如图,线段BH即为所求.
(3)图中AC与A1C1的关系是AC=A1C1,AC∥A1C1.
故答案为:AC=A1C1,AC∥A1C1.
(4)平移中线段AC扫过部分的面积是 5×4+2×4=28.
【变式5-3】(2023春 兴化市期末)如图,方格纸中每个小正方形的边长都是1,△ABC是格点三角形(三个顶点都在格点上).△ABC经过平移后得到△A'B'C',点B恰好落在点B'处,
(1)请画出平移后的△A'B'C';
(2)△A'B'C'的面积等于 ;
(3)在线段PQ上是否存在格点M,使得△MA'C'的面积是△MA'B'面积的2倍?若存在,请画出所有这样的格点M1,M2,…,若不存在,请说明理由.
【分析】(1)将三个顶点分别向左平移5个单位、向上平移2个单位得到其对应点,再首尾顺次连接即可;
(2)利用割补法,用长为2、宽为6的矩形面积减去四周的三个三角形的面积即可;
(3)根据三个三角形的高相同,要使△MA'C'的面积是△MA'B'面积的2倍只需使对应底边的长度满足2倍的关系即可.
【解答】解:(1)画出平移后的△A'B'C';
(2)△A'B'C'的面积等于3×63×32×31×6,
故答案为:;
(3)如图所示,点M1、M2即为所求.
【题型6 平移中几何综合问题】
【例6】(2023秋 吉林期末)如图,点C、M、N在射线DQ上,点B在射线AP上,且AP∥DQ,∠D=∠ABC=80°,∠1=∠2,AN平分∠DAM.
(1)试说明AD∥BC的理由;
(2)试求∠CAN的度数;
(3)平移线段BC.
①试问∠AMD:∠ACD的值是否发生变化?若不会,请求出这个比值;若会,请找出相应变化规律;
②若在平移过程中存在某种位置,使得∠AND=∠ACB,试求此时∠ACB的度数.
【分析】(1)根据平行线的性质和判定解答即可;
(2)根据角平分线的定义解答即可;
(3)根据平移的性质和平行线的性质解答即可.
【解答】解:(1)∵AP∥DQ,
∴∠D+∠DAB=180°.
∵∠D=80°,
∴∠DAB=100°.
∵∠ABC=80°,
∴∠DAB+∠ABC=180°,
∴AD∥BC;
(2)∵AN平分∠DAM,
∴∠NAM=∠NAD∠DAM.
∵∠1=∠2,
∴∠CAM∠BAM.
∴∠NAM+∠CAM∠DAM∠BAM,
即:∠CAN∠DAB
∵∠DAB=100°,
∴∠CAN=50°,
(3)①不会.
∵AP∥DQ,
∴∠AMD=∠MAB=2∠1,∠ACD=∠1,
∴∠AMD:∠ACD=2,
②∵AP∥DQ,AD∥BC,
∴∠AND=∠NAB,∠ACB=∠DAC,
∵∠AND=∠ACB,
∴∠NAB=∠DAC,
∴∠NAB﹣∠NAC=∠DAC﹣∠NAC,
即:∠1=∠DAN.
∴∠1=∠2=∠DAN=∠MAN=25°,
∴∠ACB=∠DAC=75°.
【变式6-1】(2023春 吉林月考)如图,AM∥BN,线段CD的两个端点C,D分别在射线BN,AM上,且∠A=∠BCD=108°,E是线段AD上一点(不与点A、D重合),BD平分∠EBC.
(1)求∠ABC的度数;
(2)请在图中找出与∠ABC相等的角,并说明理由;
(3)若平行移动CD,那么∠ADB与∠AEB的度数之比是否随着CD位置的变化而发生变化?若变化,找出变化规律;若不变,求出这个比值.
【分析】(1)由“两直线平行,同旁内角互补”求得∠ABC的度数;
(2)与∠ABC相等的角:∠ADC,∠DCN.根据平行线的性质进行证明即可;
(3)由平行线的性质和角平分线的定义推知.
【解答】解:(1)∵AM∥BN,
∴∠A+∠ABC=180°,
∴∠ABC=180°﹣∠A=180108°=72°;
(2)与∠ABC相等的角:∠ADC,∠DCN.
理由:∵AM∥BN,
∠ADC=∠DCN,∠ADC+∠BCD=180°,
∴∠ADC=180°﹣∠BCD=72°,
∴∠DCN=72°,
∴∠ADC=∠DCN=∠ABC;
(3)不发生变化.
∵AM∥BN,
∴∠AEB=∠EBC,∠ADB=∠DBC.
∵BD平分∠EBC,
∴∠DBC∠EBC,
∴∠ADB∠AEB,
∴.
【变式6-2】如图,已知直线AB∥CD,∠A=∠C=100°,E、F在CD上,且满足∠DBF=∠ABD,BE平分∠CBF.
(1)求∠DBE的度数.
(2)若平行移动AD,那么∠BFC:∠BDC的比值是否随之发生变化?若变化,找出变化规律;若不变,求出这个比值.
(3)在平行移动AD的过程中,是否存在某种情况,使∠BEC=∠ADB?若存在,求出其度数;若不存在,请说明理由.
【分析】(1)由直线AB∥CD,根据两直线平行,同旁内角互补,即可求得∠ABC的度数,又由∠DBE∠ABC,即可求得∠DBE的度数.
(2)由直线AB∥CD,根据两直线平行,内错角相等,即可求得∠BFC=∠ABF=2∠ABD,∠ABD=∠BDC,继而可求得∠BFC:∠BDC的比值;
(3)首先设∠ABD=∠DBF=∠BDC=x°,由直线AB∥CD,根据两直线平行,同旁内角互补与两直线平行,内错角相等,可求得∠BEC与∠ADB的度数,又由∠BEC=∠ADB,即可得方程:x°+40°=80°﹣x°,解此方程即可求得答案.
【解答】解:(1)∵AB∥CD,
∴∠ABC=180°﹣∠C=80°,
∵∠DBF=∠ABD,BE平分∠CBF,
∴∠DBE∠ABF∠CBF∠ABC=40°;
(2)不变.
理由∵AB∥CD,
∴∠BFC=∠ABF=2∠ABD,∠ABD=∠BDC,
∴∠BFC=2∠BDC,
∴∠BFC:∠BDC=2:1;
(3)存在.
设∠ABD=∠DBF=∠BDC=x°.
∵AB∥CD,
∴∠BEC=∠ABE=x°+40°;
∵AB∥CD,
∴∠ADC=180°﹣∠A=80°,
∴∠ADB=80°﹣x°.
若∠BEC=∠ADB,
则x°+40°=80°﹣x°,
得x°=20°.
∴存在∠BEC=∠ADB=60°.
【变式6-3】(2023春 奉化区校级期末)如图,AB∥CD,点C在点D的右侧,∠ABC,∠ADC的平分线交于点E(不与B,D点重合),∠ADC=70°.设∠BED=n°.
(1)若点B在点A的左侧,求∠ABC的度数;(用含n的代数式表示)
(2)将(1)中的线段BC沿DC方向平移,当点B移动到点A右侧时,请画出图形并判断∠ABC的度数是否改变.若改变,请求出∠ABC的度数(用含n的代数式表示);若不变,请说明理由.
【分析】根据平行线的性质即可求解.
【解答】解:(1)如图1,过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠ABE=∠BEF,∠CDE=∠DEF,
∵BE平分∠ABC,DE平分∠ADC,∠ADC=70°,
∴∠ABC=2∠ABE=2∠BEF,,
∵∠BED=n°,
∴∠BEF=(n﹣35)°,
∴∠ABC=2∠BEF=2(n﹣35)°=(2n﹣70)°;
(2)∠ABC的度数改变,
画出的图形如图2,过点E作EF∥AB,
∵BE平分∠ABC,DE平分∠ADC,∠ADC=70°,
∴∠ABC=2∠ABE,,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠ABE+∠BEF=180°,∠CDE=∠DEF=35°,
∵∠BED=n°,
∴∠BEF=(n﹣35)°,
∴∠ABE=180°﹣∠BEF=180°﹣(n﹣35)°=180°﹣n°+35°=(215﹣n)°,
∴∠ABC=2∠ABE=2(215﹣n)°=(430﹣2n)°.
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
