浙教版2023-2024学年七年级下册 平行线的性质与判定综合运用 解答题推理填空专项训练(无答案)
文档属性
| 名称 | 浙教版2023-2024学年七年级下册 平行线的性质与判定综合运用 解答题推理填空专项训练(无答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-05 10:07:39 | ||
图片预览


文档简介
浙教版2023-2024学年七年级下册《平行线的性质与判定综合运用》
解答题推理填空专项训练
1.请为下面的推理填上依据:
如图,因为∥
所以∠2=∠3( )
又∠3+∠1=,
所以∠1+∠2=( )
2.如图,已知∠1=∠3,CD∥EF,试说明∠1=∠4.请将过程填写完整.
解:∵∠1=∠3,
又∠2=∠3(_______),
∴∠1=____,
∴______∥______(_______),
又∵CD∥EF,
∴AB∥_____,
∴∠1=∠4(两直线平行,同位角相等).
3.已知:如图,AB∥CD,∠A=∠D
求证:AF∥ED
请你将证明过程补充完整
证明:∵AB∥CD,
∴______=______(______),
∵∠A=∠D,
∴______=______(______),
∴AF∥ED(______).
4.已知:如图,AB∥DE,∠1=∠2,则AE与DC平行吗?完成下列推理,并把每一步的依据填写在后面的括号内
解:∵AB∥DE (已知)
∴∠1=∠AED ( )
∵∠1=∠2 (已知)
∴∠ =∠ ( )
∴AE∥DC ( )
5.如图,填写证明过程和理由
∵ ∠1 +∠2=180° (已知)
∴_____∥_______( )
∵∠3=∠4(已知)
∴_____∥_______( )
∴a∥c( )
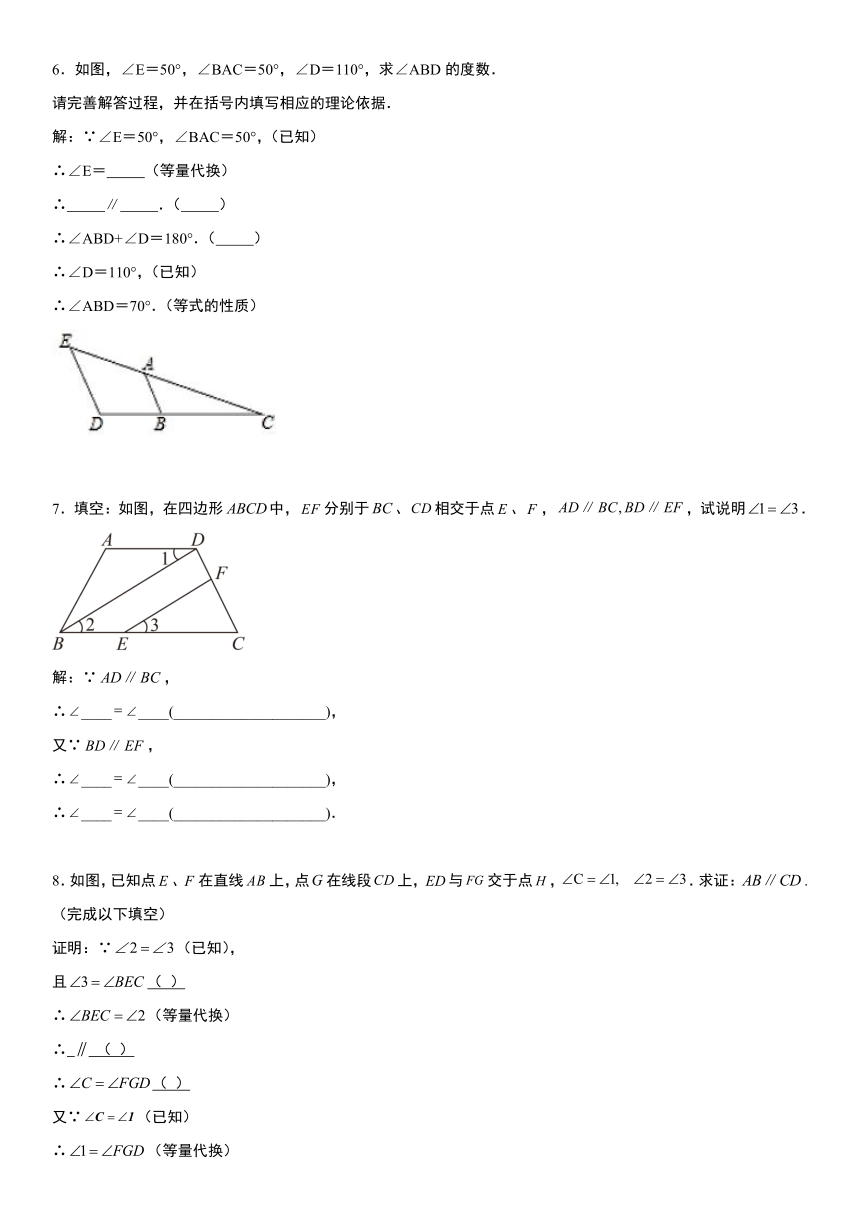
6.如图,∠E=50°,∠BAC=50°,∠D=110°,求∠ABD的度数.
请完善解答过程,并在括号内填写相应的理论依据.
解:∵∠E=50°,∠BAC=50°,(已知)
∴∠E= (等量代换)
∴ ∥ .( )
∴∠ABD+∠D=180°.( )
∴∠D=110°,(已知)
∴∠ABD=70°.(等式的性质)
7.填空:如图,在四边形中,分别于、相交于点、,,试说明.
解:∵,
∴________(____________________),
又∵,
∴________(____________________),
∴________(____________________).
8.如图,已知点、在直线上,点在线段上,与交于点,.求证:.
(完成以下填空)
证明:∵(已知),
且( )
∴(等量代换)
∴ ( )
∴( )
又∵(已知)
∴(等量代换)
∴( )
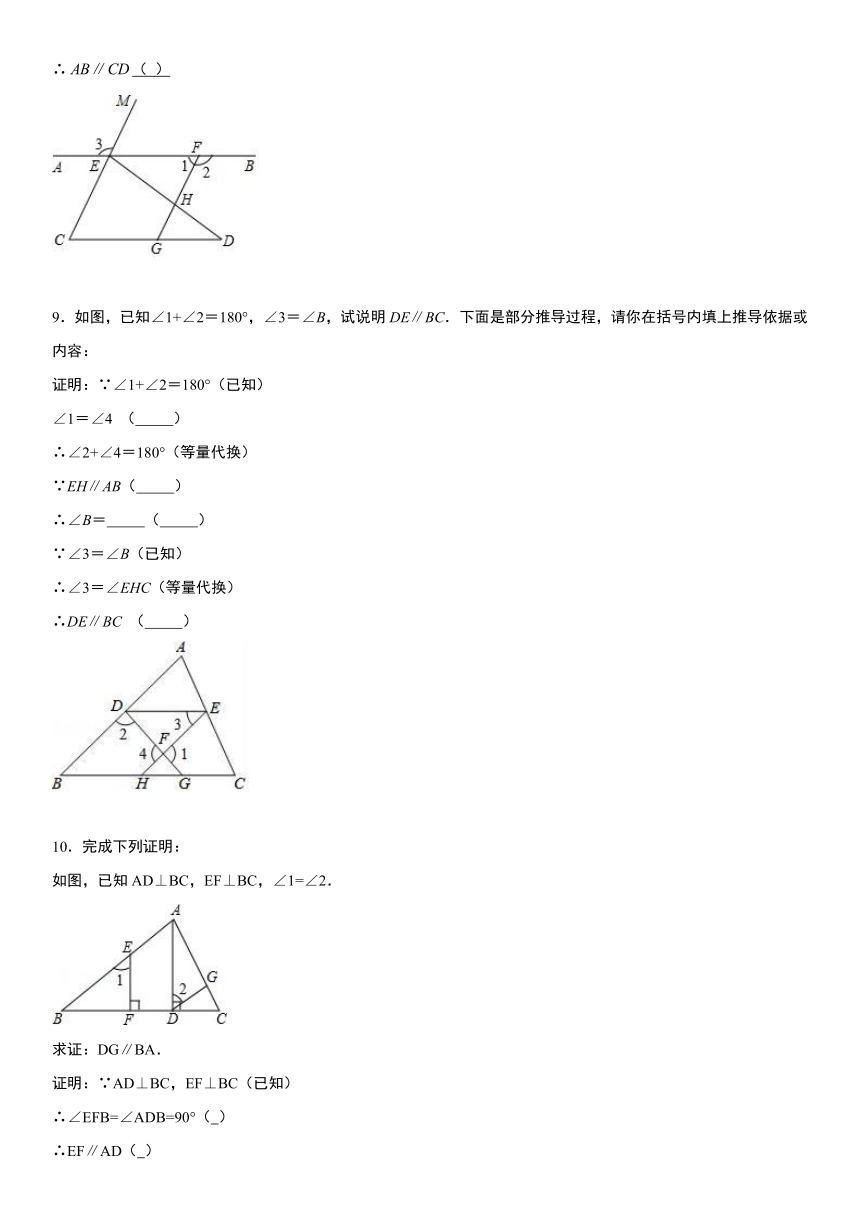
9.如图,已知∠1+∠2=180°,∠3=∠B,试说明DE∥BC.下面是部分推导过程,请你在括号内填上推导依据或内容:
证明:∵∠1+∠2=180°(已知)
∠1=∠4 ( )
∴∠2+∠4=180°(等量代换)
∵EH∥AB( )
∴∠B= ( )
∵∠3=∠B(已知)
∴∠3=∠EHC(等量代换)
∴DE∥BC ( )
10.完成下列证明:
如图,已知AD⊥BC,EF⊥BC,∠1=∠2.
求证:DG∥BA.
证明:∵AD⊥BC,EF⊥BC(已知)
∴∠EFB=∠ADB=90°( )
∴EF∥AD( )
∴∠1=∠BAD( )
又∵∠1=∠2(已知)
∴ (等量代换)
∴DG∥BA.( )
11.如图.,.
(1)试说明:;
∵,(已知)
∴∠___________( )
又∵,(已知)
∴___________(等量代换)
∴( )
(2)与的位置关系如何?为什么?
与的位置关系是:___________理由如下:
∵,(已知)
∴___________(两直线平行,内错角相等)
又∵,(已知)
∴___________(等量代换)
∴___________.( )
12.在下面的括号内,填上推理的依据.
已知:如图,,.求证:.
证明:∵( ),
又∵(_________),
∴( ).
∴( ).
∴( ).
又∵(已知),
∴( ).
∴( ).
∴∠A=∠F( ).
13.如图,已知,,,求证:
证明:(已知)
________( )
(已知)
________(等量代换)
又(已知)
(等式性质)
即________________
________( )
( )
14.如图,已知,,,试说明:.完善下面的解答过程,并填写理由或数学式:
解:∵(已知)
∴_________(_________)
∴(_________)
∵(已知)
∴_________(_________)
∴(_________)
∴(_________)
即
∴(已知)
∴
即_________
∴(_________).
15.如图,平分,,,则也是的平分线,完成下列推理过程.
证明:是的平分线(已知),
( ).
(已知),
( ).
( ).
又(已知),
( ).
( ).
( ).
16.完成下面的证明.
如图:,平分,平分,求证:.
证明:因为,所以__________,
因为平分,平分,
所以__________,__________,
所以____________________,
所以( )
17.请把证明的过程补充完整,并在括号内写上依据.
如图,,,.请把证明的过程补充完整,并在括号内写上依据.
证明:∵,
∴ ( )
∵,
∴
即∠ =∠ .
∵,
∴
∴ ( ).
18.完成下面推理过程,并在括号内填上推理依据.
如图,四边形中,,,的平分线交边于点E,并与延长线交点F,求证:.
证明:∵(已知),
∴(______),
∴______(两直线平行,同位角相等),
∵,(已知),
∴,
∴______ (同旁内角互补,两直线平行),
∴(______)
∵平分(已知),
∴(角平分线定义),
∴______,
∴.
解答题推理填空专项训练
1.请为下面的推理填上依据:
如图,因为∥
所以∠2=∠3( )
又∠3+∠1=,
所以∠1+∠2=( )
2.如图,已知∠1=∠3,CD∥EF,试说明∠1=∠4.请将过程填写完整.
解:∵∠1=∠3,
又∠2=∠3(_______),
∴∠1=____,
∴______∥______(_______),
又∵CD∥EF,
∴AB∥_____,
∴∠1=∠4(两直线平行,同位角相等).
3.已知:如图,AB∥CD,∠A=∠D
求证:AF∥ED
请你将证明过程补充完整
证明:∵AB∥CD,
∴______=______(______),
∵∠A=∠D,
∴______=______(______),
∴AF∥ED(______).
4.已知:如图,AB∥DE,∠1=∠2,则AE与DC平行吗?完成下列推理,并把每一步的依据填写在后面的括号内
解:∵AB∥DE (已知)
∴∠1=∠AED ( )
∵∠1=∠2 (已知)
∴∠ =∠ ( )
∴AE∥DC ( )
5.如图,填写证明过程和理由
∵ ∠1 +∠2=180° (已知)
∴_____∥_______( )
∵∠3=∠4(已知)
∴_____∥_______( )
∴a∥c( )
6.如图,∠E=50°,∠BAC=50°,∠D=110°,求∠ABD的度数.
请完善解答过程,并在括号内填写相应的理论依据.
解:∵∠E=50°,∠BAC=50°,(已知)
∴∠E= (等量代换)
∴ ∥ .( )
∴∠ABD+∠D=180°.( )
∴∠D=110°,(已知)
∴∠ABD=70°.(等式的性质)
7.填空:如图,在四边形中,分别于、相交于点、,,试说明.
解:∵,
∴________(____________________),
又∵,
∴________(____________________),
∴________(____________________).
8.如图,已知点、在直线上,点在线段上,与交于点,.求证:.
(完成以下填空)
证明:∵(已知),
且( )
∴(等量代换)
∴ ( )
∴( )
又∵(已知)
∴(等量代换)
∴( )
9.如图,已知∠1+∠2=180°,∠3=∠B,试说明DE∥BC.下面是部分推导过程,请你在括号内填上推导依据或内容:
证明:∵∠1+∠2=180°(已知)
∠1=∠4 ( )
∴∠2+∠4=180°(等量代换)
∵EH∥AB( )
∴∠B= ( )
∵∠3=∠B(已知)
∴∠3=∠EHC(等量代换)
∴DE∥BC ( )
10.完成下列证明:
如图,已知AD⊥BC,EF⊥BC,∠1=∠2.
求证:DG∥BA.
证明:∵AD⊥BC,EF⊥BC(已知)
∴∠EFB=∠ADB=90°( )
∴EF∥AD( )
∴∠1=∠BAD( )
又∵∠1=∠2(已知)
∴ (等量代换)
∴DG∥BA.( )
11.如图.,.
(1)试说明:;
∵,(已知)
∴∠___________( )
又∵,(已知)
∴___________(等量代换)
∴( )
(2)与的位置关系如何?为什么?
与的位置关系是:___________理由如下:
∵,(已知)
∴___________(两直线平行,内错角相等)
又∵,(已知)
∴___________(等量代换)
∴___________.( )
12.在下面的括号内,填上推理的依据.
已知:如图,,.求证:.
证明:∵( ),
又∵(_________),
∴( ).
∴( ).
∴( ).
又∵(已知),
∴( ).
∴( ).
∴∠A=∠F( ).
13.如图,已知,,,求证:
证明:(已知)
________( )
(已知)
________(等量代换)
又(已知)
(等式性质)
即________________
________( )
( )
14.如图,已知,,,试说明:.完善下面的解答过程,并填写理由或数学式:
解:∵(已知)
∴_________(_________)
∴(_________)
∵(已知)
∴_________(_________)
∴(_________)
∴(_________)
即
∴(已知)
∴
即_________
∴(_________).
15.如图,平分,,,则也是的平分线,完成下列推理过程.
证明:是的平分线(已知),
( ).
(已知),
( ).
( ).
又(已知),
( ).
( ).
( ).
16.完成下面的证明.
如图:,平分,平分,求证:.
证明:因为,所以__________,
因为平分,平分,
所以__________,__________,
所以____________________,
所以( )
17.请把证明的过程补充完整,并在括号内写上依据.
如图,,,.请把证明的过程补充完整,并在括号内写上依据.
证明:∵,
∴ ( )
∵,
∴
即∠ =∠ .
∵,
∴
∴ ( ).
18.完成下面推理过程,并在括号内填上推理依据.
如图,四边形中,,,的平分线交边于点E,并与延长线交点F,求证:.
证明:∵(已知),
∴(______),
∴______(两直线平行,同位角相等),
∵,(已知),
∴,
∴______ (同旁内角互补,两直线平行),
∴(______)
∵平分(已知),
∴(角平分线定义),
∴______,
∴.
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
