3.3多项式的乘法(1) 课件(共17张PPT)
文档属性
| 名称 | 3.3多项式的乘法(1) 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 326.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-13 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
3.3 多项式的乘法(1)
第3章 整式的乘除
浙教版 七年级下册
课前复习
积的乘方等于各因数乘方的积.
(3)积的乘方法则:
(ab)n = anbn (n为正整数)
幂的乘方,底数不变,指数相乘.
(am)n=(an)m=amn (m、n都是正整数)
同底数幂相乘,底数不变,指数相加.
am · an =am+n (m、n都是正整数)
(2)同底数幂的乘法法则:
(1)幂的乘方法则:
课前复习
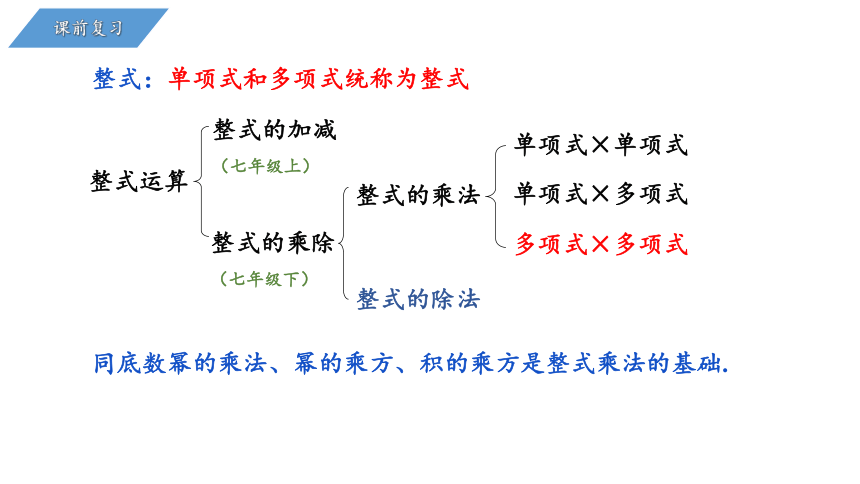
整式:单项式和多项式统称为整式
整式运算
整式的加减
(七年级上)
整式的乘除
(七年级下)
整式的乘法
同底数幂的乘法、幂的乘方、积的乘方是整式乘法的基础.
单项式×单项式
单项式×多项式
多项式×多项式
整式的除法
课前练习
【练习】 计算
新知探究
【探究】 计算:
【猜想】由以上计算猜想以下多项式乘以多项式的结果.
新知探究
证明(分配律):设 x=b+m,则
(a+n)(b+m) = (a+n)x
= a(b+m)+n(b+m)
= ab+am+nb+nm
证明:(a+n)(b+m) = ab+am+nb+nm
即(a+n)(b+m)
=ab+am+nb+nm
= ax+nx
新知探究
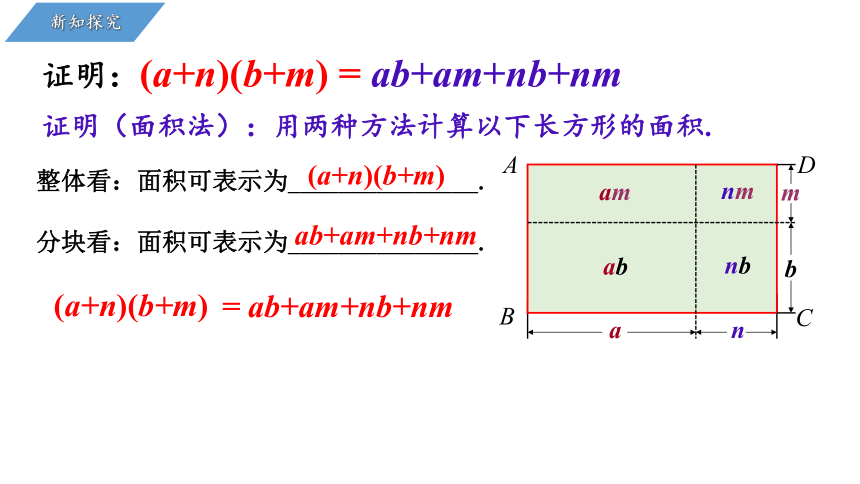
证明(面积法):用两种方法计算以下长方形的面积.
证明:(a+n)(b+m) = ab+am+nb+nm
(a+n)(b+m)
= ab+am+nb+nm
整体看:面积可表示为_______________.
分块看:面积可表示为_______________.
(a+n)(b+m)
ab+am+nb+nm
a
n
b
m
ab
am
nm
nb
A
B
D
C
新知探究
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
(a+n)(b+m)
ab
+
am
+
nb
+
nm
ax+ay+az
+bx+by+bz
【新知】多项式与多项式相乘的法则:
【例1】 计算
例题讲解
(2)(3a 1)( a+3)
=3x2
-6xy
+xy
-2y2
=3x2-5xy-2y2
=3a2
=3a2+8a-3
+9a
-a
-3
(1)(3x + y)(x 2y)
【思考】式子展开后的项数与原来两个多项式的项数有什么关系?
在合并同类项之前,展开式的项数恰好等于两个多项式的项数的积.
(3)(3x + y)(x 2y+2)
学以致用
【练习】 计算:
(2a 3)(3a + 1) 6a(a 4),其中a =
【例2】先化简,再求值:
例题讲解
【变式】化简:(2a 3)(3a + 1) (6 a)(a 4)
学以致用
【练习】 化简:
解:(1)原式
(1) (2x 1)( 3x) (1 3x)(1+2x)
(2) 2(x 8)(x 5) (2x 1)(x+2)
解:(2)原式
学以致用
例题讲解
学以致用
我们已经知道,根据几何图形的面积关系可以说明(a+n)(b+m)=ab+am+nb+mn.实际上还有一些等式也可以用这种方式加以说明,例如:(2a+b)(a+b)=2a2+3ab+b2,就可以用图1的面积关系来说明.
(1)根据图2写出一个等式: _______________________________.
(2)已知等式:(x+1)(x+3)=x2+4x+3,请你画出一个相应的几何图形加以说明(仿照图1或图2画出图形即可).
(2a+b)(a+2b)=2a2+5ab+2b2
解:(2)画出相应的几何图形如答图.
课堂总结
1.多项式与多项式相乘的法则
3. 数学思想:数形结合、整体思想、化归思想.
2.法则应用的注意事项:
(1)要有序地逐项相乘,不要漏乘;
(2)去括号时注意符号;
(3)化简结果要最简(即不含有同类项).
作业布置
1. 作业本1:3.3单项式的乘法(1)
2. 作业订正和自主练习.
3.3 多项式的乘法(1)
第3章 整式的乘除
浙教版 七年级下册
课前复习
积的乘方等于各因数乘方的积.
(3)积的乘方法则:
(ab)n = anbn (n为正整数)
幂的乘方,底数不变,指数相乘.
(am)n=(an)m=amn (m、n都是正整数)
同底数幂相乘,底数不变,指数相加.
am · an =am+n (m、n都是正整数)
(2)同底数幂的乘法法则:
(1)幂的乘方法则:
课前复习
整式:单项式和多项式统称为整式
整式运算
整式的加减
(七年级上)
整式的乘除
(七年级下)
整式的乘法
同底数幂的乘法、幂的乘方、积的乘方是整式乘法的基础.
单项式×单项式
单项式×多项式
多项式×多项式
整式的除法
课前练习
【练习】 计算
新知探究
【探究】 计算:
【猜想】由以上计算猜想以下多项式乘以多项式的结果.
新知探究
证明(分配律):设 x=b+m,则
(a+n)(b+m) = (a+n)x
= a(b+m)+n(b+m)
= ab+am+nb+nm
证明:(a+n)(b+m) = ab+am+nb+nm
即(a+n)(b+m)
=ab+am+nb+nm
= ax+nx
新知探究
证明(面积法):用两种方法计算以下长方形的面积.
证明:(a+n)(b+m) = ab+am+nb+nm
(a+n)(b+m)
= ab+am+nb+nm
整体看:面积可表示为_______________.
分块看:面积可表示为_______________.
(a+n)(b+m)
ab+am+nb+nm
a
n
b
m
ab
am
nm
nb
A
B
D
C
新知探究
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
(a+n)(b+m)
ab
+
am
+
nb
+
nm
ax+ay+az
+bx+by+bz
【新知】多项式与多项式相乘的法则:
【例1】 计算
例题讲解
(2)(3a 1)( a+3)
=3x2
-6xy
+xy
-2y2
=3x2-5xy-2y2
=3a2
=3a2+8a-3
+9a
-a
-3
(1)(3x + y)(x 2y)
【思考】式子展开后的项数与原来两个多项式的项数有什么关系?
在合并同类项之前,展开式的项数恰好等于两个多项式的项数的积.
(3)(3x + y)(x 2y+2)
学以致用
【练习】 计算:
(2a 3)(3a + 1) 6a(a 4),其中a =
【例2】先化简,再求值:
例题讲解
【变式】化简:(2a 3)(3a + 1) (6 a)(a 4)
学以致用
【练习】 化简:
解:(1)原式
(1) (2x 1)( 3x) (1 3x)(1+2x)
(2) 2(x 8)(x 5) (2x 1)(x+2)
解:(2)原式
学以致用
例题讲解
学以致用
我们已经知道,根据几何图形的面积关系可以说明(a+n)(b+m)=ab+am+nb+mn.实际上还有一些等式也可以用这种方式加以说明,例如:(2a+b)(a+b)=2a2+3ab+b2,就可以用图1的面积关系来说明.
(1)根据图2写出一个等式: _______________________________.
(2)已知等式:(x+1)(x+3)=x2+4x+3,请你画出一个相应的几何图形加以说明(仿照图1或图2画出图形即可).
(2a+b)(a+2b)=2a2+5ab+2b2
解:(2)画出相应的几何图形如答图.
课堂总结
1.多项式与多项式相乘的法则
3. 数学思想:数形结合、整体思想、化归思想.
2.法则应用的注意事项:
(1)要有序地逐项相乘,不要漏乘;
(2)去括号时注意符号;
(3)化简结果要最简(即不含有同类项).
作业布置
1. 作业本1:3.3单项式的乘法(1)
2. 作业订正和自主练习.
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
