3.4 乘法公式(第1课时) 课件(共14张PPT)
文档属性
| 名称 | 3.4 乘法公式(第1课时) 课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 638.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-18 00:00:00 | ||
图片预览






文档简介
(共14张PPT)
浙教版数学 七年级下
3.4 乘法公式
第1课时
学习目标
1. 掌握平方差公式,会利用平方差公式计算;
2.能运用平方差公式进行简便计算.
回顾:多项式的乘法法则
多项式与多项式相乘, 先用一个多项式的每一项乘以另一个多项式的每一项, 再把所得的积相加.
=
ab
1
2
3
4
+am
+nb
+mn
1
2
3
4
(a+n)(b+m)
思考:两项乘两项的结果
一定是四项吗?
算一算:计算下列各题:
(a+2)(a-2)=_____________
(3-x)(3+x)=_____________
(a+b)(a-b )=_____________
(4) (2m+n)(2m-n)=__________
议一议:比较等号两边的代数式,它们在系数和字母方面各有什么特点 你发现了什么规律?
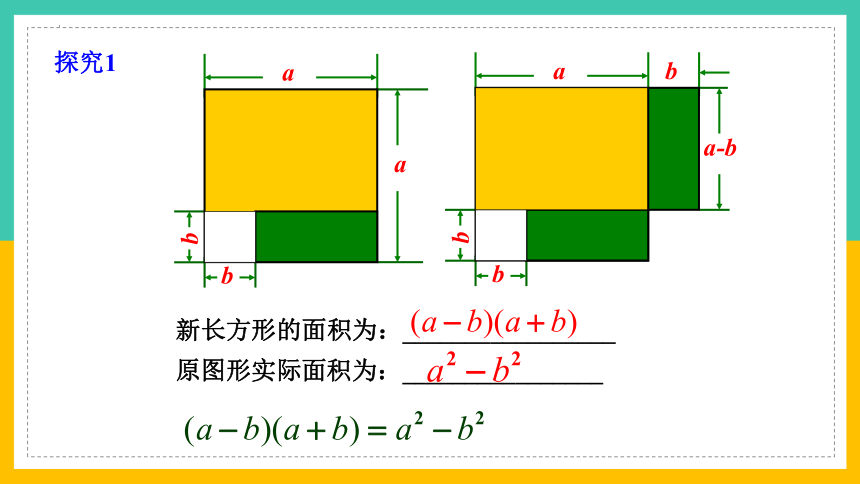
探究1
原图形实际面积为:________________
新长方形的面积为:_________________
b
a
a
b
a-b
b
b
a
b
做一做
1、下列两个多项式相乘,哪些可以用平方差公式?
哪些不能?
例题讲解
例1 运用平方差公式计算:
解:
例2 用平方差公式计算:
解:
做一做,作业题1,3,5,7
1、计算:
(1) 102×98;
(2) (y+2) (y-2) – (y-1) (y+5) .
解: (1)102×98
=(100+2)(100-2)
= 1002-22
=10000 – 4
= 9996.
(2)(y+2)(y-2)- (y-1)(y+5)
= y2-22-(y2+4y-5)
= y2-4-y2-4y+5
= - 4y + 1.
平方差公式:
(a+b)(a- b) =
a2- b2.
即两数和与这两数差的积等于这两个数的平方差.
注:这里的两数可以是数字、字母、单项式也可以是两个多项式等.
左边:是两个二项式相乘,并且有一项完全相同;另一项互为相反数。
右边:是乘式中两项的平方差,即:
(相同项)2-(相反项)2
达标测评
1.下列各式中能用平方差公式是( )
A.(x+y)(y+x)
B.(x+y)(y﹣x)
C.(x+y)(﹣y﹣x)
D.(﹣x+y)(y﹣x)
B
2.下列各式中,与(1﹣a)(﹣a﹣1)相等的是( )
A.a2﹣1 B.a2﹣2a+1
C.a2﹣2a﹣1 D.a2+1
A
3.先化简(a+1)(a﹣1)+a(1﹣a)﹣a,再根据化简结果,你发现该代数式的值与a的取值有什么关系?
解:原式=a2﹣1+a﹣a2﹣a=﹣1.
该代数式与a的取值没有关系.
小结
通过本节课的内容,你有哪些收获?
1.试用语言表述平方差公式 (a+b)(a b)=a2 b2
两数和与这两数差的积,等于它们的平方差.
2.步骤:找出相等的“项”和符号相反的“项”,然后应用公式.
浙教版数学 七年级下
3.4 乘法公式
第1课时
学习目标
1. 掌握平方差公式,会利用平方差公式计算;
2.能运用平方差公式进行简便计算.
回顾:多项式的乘法法则
多项式与多项式相乘, 先用一个多项式的每一项乘以另一个多项式的每一项, 再把所得的积相加.
=
ab
1
2
3
4
+am
+nb
+mn
1
2
3
4
(a+n)(b+m)
思考:两项乘两项的结果
一定是四项吗?
算一算:计算下列各题:
(a+2)(a-2)=_____________
(3-x)(3+x)=_____________
(a+b)(a-b )=_____________
(4) (2m+n)(2m-n)=__________
议一议:比较等号两边的代数式,它们在系数和字母方面各有什么特点 你发现了什么规律?
探究1
原图形实际面积为:________________
新长方形的面积为:_________________
b
a
a
b
a-b
b
b
a
b
做一做
1、下列两个多项式相乘,哪些可以用平方差公式?
哪些不能?
例题讲解
例1 运用平方差公式计算:
解:
例2 用平方差公式计算:
解:
做一做,作业题1,3,5,7
1、计算:
(1) 102×98;
(2) (y+2) (y-2) – (y-1) (y+5) .
解: (1)102×98
=(100+2)(100-2)
= 1002-22
=10000 – 4
= 9996.
(2)(y+2)(y-2)- (y-1)(y+5)
= y2-22-(y2+4y-5)
= y2-4-y2-4y+5
= - 4y + 1.
平方差公式:
(a+b)(a- b) =
a2- b2.
即两数和与这两数差的积等于这两个数的平方差.
注:这里的两数可以是数字、字母、单项式也可以是两个多项式等.
左边:是两个二项式相乘,并且有一项完全相同;另一项互为相反数。
右边:是乘式中两项的平方差,即:
(相同项)2-(相反项)2
达标测评
1.下列各式中能用平方差公式是( )
A.(x+y)(y+x)
B.(x+y)(y﹣x)
C.(x+y)(﹣y﹣x)
D.(﹣x+y)(y﹣x)
B
2.下列各式中,与(1﹣a)(﹣a﹣1)相等的是( )
A.a2﹣1 B.a2﹣2a+1
C.a2﹣2a﹣1 D.a2+1
A
3.先化简(a+1)(a﹣1)+a(1﹣a)﹣a,再根据化简结果,你发现该代数式的值与a的取值有什么关系?
解:原式=a2﹣1+a﹣a2﹣a=﹣1.
该代数式与a的取值没有关系.
小结
通过本节课的内容,你有哪些收获?
1.试用语言表述平方差公式 (a+b)(a b)=a2 b2
两数和与这两数差的积,等于它们的平方差.
2.步骤:找出相等的“项”和符号相反的“项”,然后应用公式.
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
