5.4乘法公式1-平方差公式(浙江省温州市)
文档属性
| 名称 | 5.4乘法公式1-平方差公式(浙江省温州市) |  | |
| 格式 | rar | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-05-14 13:27:00 | ||
图片预览




文档简介
课件24张PPT。5.4乘法公式(1)仔细观察2组题目,你们能发现它们之间的不同之处吗赛一赛(男女分组比赛看哪组算的快又准)
男生组 女生组
① (x-1)(x-2) ① (x-1)(x+1)
②(a+1)(a+2) ②(a+2)(a-2)
③ (x-3)(x+2) ③ (x-5)(x+5)
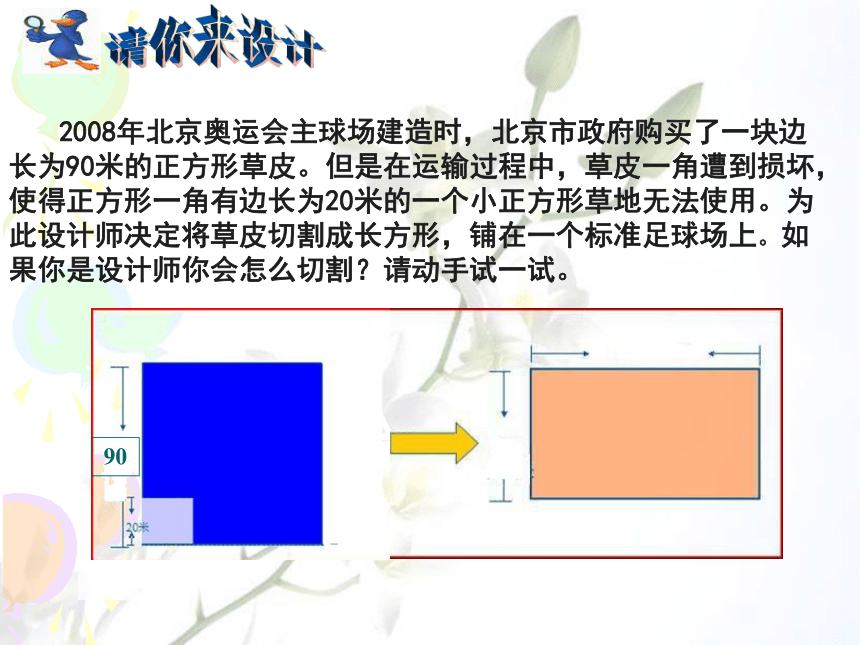
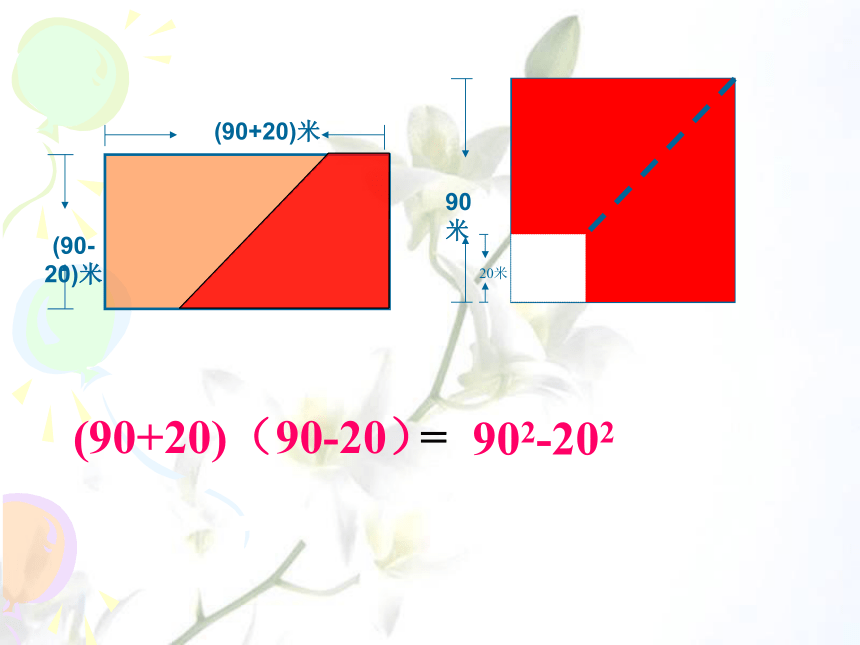
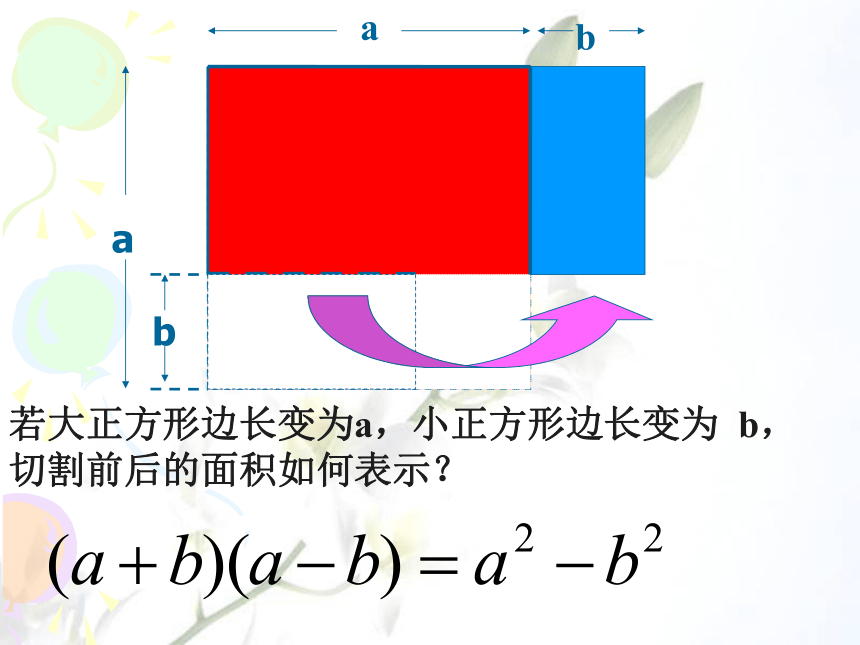
2008年北京奥运会主球场建造时,北京市政府购买了一块边长为90米的正方形草皮。但是在运输过程中,草皮一角遭到损坏,使得正方形一角有边长为20米的一个小正方形草地无法使用。为此设计师决定将草皮切割成长方形,铺在一个标准足球场上。如果你是设计师你会怎么切割?请动手试一试。请你来设计90902-202(90+20)(90-20)=若大正方形边长变为a,小正方形边长变为 b,切割前后的面积如何表示?探究:是否(a+b)(a-b)=a2-b2一定成立?你可以用你已学过的多项式乘法知识来验证吗?多项式乘多项式法则合并同类项(a+b)(a-b)=a2-ab+ab-b2=a2-b2结论:通过图形和多项式乘多项式知识, 我们都证明了这个式子的成立。
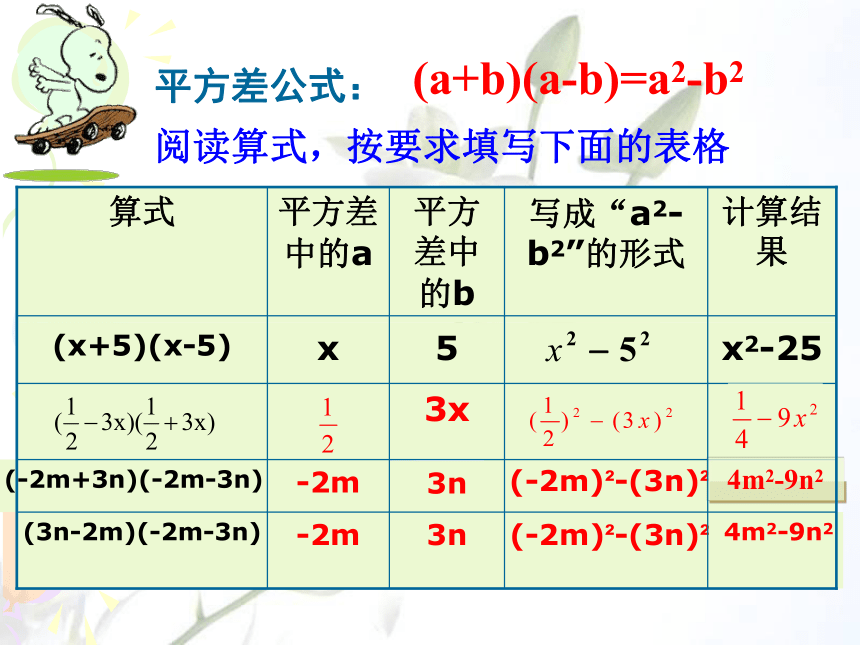
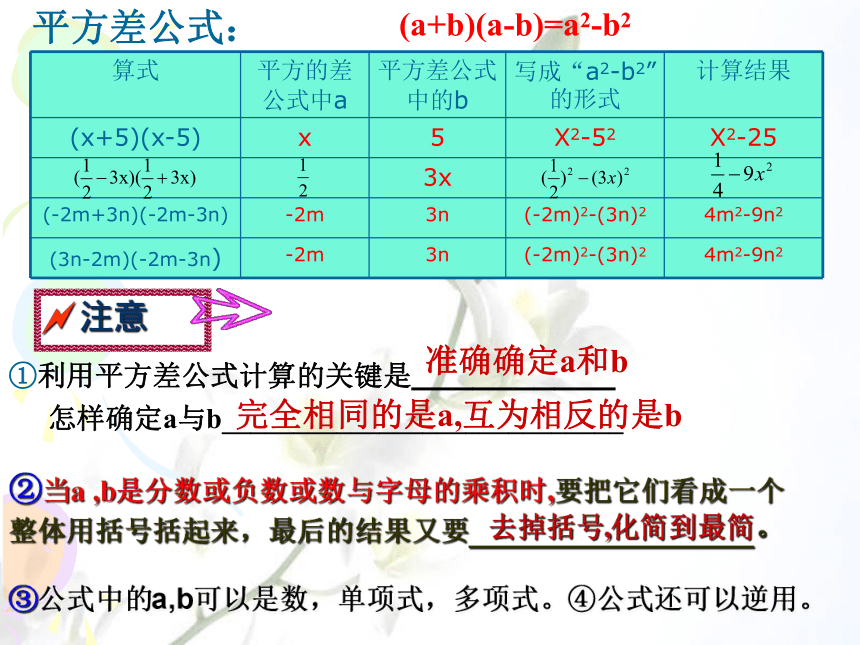
推得公式:(a+b)(a?b)=a2?b2两数和与这两数差的积这两数的平方差.等于平方差公式:左边是两个项数相同的多项式相乘,并且有一部分完全相同,另一部分互相相反。(3n-2m)(-2m-3n)(-2m)2-(3n)23n-2m(-2m+3n)(-2m-3n)3xx2-255x(x+5)(x-5)计算结果写成“a2-b2”的形式平方差中的b平方差中的a算式4m2-9n2阅读算式,按要求填写下面的表格4m2-9n2
(-2m)2-(3n)23n-2m(a+b)(a-b)=a2-b2平方差公式:②当a ,b是分数或负数或数与字母的乘积时,要把它们看成一个整体用括号括起来,最后的结果又要_________________①利用平方差公式计算的关键是__________
准确确定a和b怎样确定a与b____________________________完全相同的是a,互为相反的是b③公式中的a,b可以是数,单项式,多项式。④公式还可以逆用。去掉括号,化简到最简。平方差公式:(a+b)(a-b)=a2-b2例题精讲例1.运用平方差公式进行计算:判断并改错:
(1)(5y+2)(5y-2)=5y2-4 ( )
改正:
(2) (1- 4xy)(-1- 4xy)=1-16x2y2 ( )
改正:
(3)(-ab+3c)(-3c-ab)=a2b2-9c2 ( )
改正:
(4) (-m+7)(7-m)=m2-49 ( )
改正:(5)(x+3)(y-3)=xy-9改正:×××√原式=(- 4xy+1)(- 4xy-1)=16x2y2-1(-m+7)(7-m)=(7-m)(7-m)=49-7m-7m+m2=49-14m+m2(x+3)(y-3)=xy-3x+3y-9 ( ) :等号左边必须是有相同的项a和相反的项b,等号右边必须是(相同项)2-(相反项)2。(5y+2)(5y-2)=25y2-4×判断依据例2、你能用简便方法计算吗?
103×97 (2)59.8×60.2=x4-1(x-1)(x+1)(x2+1) (a2+b2)(a2-b2)=1-36a2b2(-6ab+1)(6ab+1)(?0.1x+4y)(?0.1x?4y)=0.01x2-16y2本节课你学到了什么?两数和与这两数差的积,等于它们的平方差。变成公式标准形式后,再用公式。要利用加法交换律,作业提示:作业本(1) (6)如果A=1234567892,B=123456788×123456790,试比较A
与 B的大小。(计算器可帮不了你哟)(4) 课外拓展:(选做)看看你能挑战到第几级!加油!!(2)(m+n+p)(m+n-p)二级挑战题:(3) (x-y)2-(x+y)2终级挑战题:(7)(2+1)(22+1)(24+1)(28+1)+1一级挑战题:(8)(3+1)(32+1)(34+1)(38+1)+1(5)12-22+32-42+52-62+...-982+992-1002+1012 从前有一个狡猾的地主,他把一块长为a米的正方形的土地租给张老汉种植,有一天,他对张老汉说:“ 我把这块地的一边减少b米,另一边增加b米,继续租给你,你也没有吃亏,你看如何?” 张老汉一听觉得没有吃亏,就答应了 ,回到家中,他把这件事对邻居讲了,邻居一听,说:“张老汉你吃亏了!”,张老汉非常吃惊。
同学们,你能告诉张老汉这是为什么吗?小故事再见让我想想我能行利用平方差公式计算:
(2+1)(22+1)(24+1)(28+1)+1=(2-1)(2+1)(22+1)(24+1)(28+1)+1=(22-1)(22+1)(24+1)(28+1)+1=216
男生组 女生组
① (x-1)(x-2) ① (x-1)(x+1)
②(a+1)(a+2) ②(a+2)(a-2)
③ (x-3)(x+2) ③ (x-5)(x+5)
2008年北京奥运会主球场建造时,北京市政府购买了一块边长为90米的正方形草皮。但是在运输过程中,草皮一角遭到损坏,使得正方形一角有边长为20米的一个小正方形草地无法使用。为此设计师决定将草皮切割成长方形,铺在一个标准足球场上。如果你是设计师你会怎么切割?请动手试一试。请你来设计90902-202(90+20)(90-20)=若大正方形边长变为a,小正方形边长变为 b,切割前后的面积如何表示?探究:是否(a+b)(a-b)=a2-b2一定成立?你可以用你已学过的多项式乘法知识来验证吗?多项式乘多项式法则合并同类项(a+b)(a-b)=a2-ab+ab-b2=a2-b2结论:通过图形和多项式乘多项式知识, 我们都证明了这个式子的成立。
推得公式:(a+b)(a?b)=a2?b2两数和与这两数差的积这两数的平方差.等于平方差公式:左边是两个项数相同的多项式相乘,并且有一部分完全相同,另一部分互相相反。(3n-2m)(-2m-3n)(-2m)2-(3n)23n-2m(-2m+3n)(-2m-3n)3xx2-255x(x+5)(x-5)计算结果写成“a2-b2”的形式平方差中的b平方差中的a算式4m2-9n2阅读算式,按要求填写下面的表格4m2-9n2
(-2m)2-(3n)23n-2m(a+b)(a-b)=a2-b2平方差公式:②当a ,b是分数或负数或数与字母的乘积时,要把它们看成一个整体用括号括起来,最后的结果又要_________________①利用平方差公式计算的关键是__________
准确确定a和b怎样确定a与b____________________________完全相同的是a,互为相反的是b③公式中的a,b可以是数,单项式,多项式。④公式还可以逆用。去掉括号,化简到最简。平方差公式:(a+b)(a-b)=a2-b2例题精讲例1.运用平方差公式进行计算:判断并改错:
(1)(5y+2)(5y-2)=5y2-4 ( )
改正:
(2) (1- 4xy)(-1- 4xy)=1-16x2y2 ( )
改正:
(3)(-ab+3c)(-3c-ab)=a2b2-9c2 ( )
改正:
(4) (-m+7)(7-m)=m2-49 ( )
改正:(5)(x+3)(y-3)=xy-9改正:×××√原式=(- 4xy+1)(- 4xy-1)=16x2y2-1(-m+7)(7-m)=(7-m)(7-m)=49-7m-7m+m2=49-14m+m2(x+3)(y-3)=xy-3x+3y-9 ( ) :等号左边必须是有相同的项a和相反的项b,等号右边必须是(相同项)2-(相反项)2。(5y+2)(5y-2)=25y2-4×判断依据例2、你能用简便方法计算吗?
103×97 (2)59.8×60.2=x4-1(x-1)(x+1)(x2+1) (a2+b2)(a2-b2)=1-36a2b2(-6ab+1)(6ab+1)(?0.1x+4y)(?0.1x?4y)=0.01x2-16y2本节课你学到了什么?两数和与这两数差的积,等于它们的平方差。变成公式标准形式后,再用公式。要利用加法交换律,作业提示:作业本(1) (6)如果A=1234567892,B=123456788×123456790,试比较A
与 B的大小。(计算器可帮不了你哟)(4) 课外拓展:(选做)看看你能挑战到第几级!加油!!(2)(m+n+p)(m+n-p)二级挑战题:(3) (x-y)2-(x+y)2终级挑战题:(7)(2+1)(22+1)(24+1)(28+1)+1一级挑战题:(8)(3+1)(32+1)(34+1)(38+1)+1(5)12-22+32-42+52-62+...-982+992-1002+1012 从前有一个狡猾的地主,他把一块长为a米的正方形的土地租给张老汉种植,有一天,他对张老汉说:“ 我把这块地的一边减少b米,另一边增加b米,继续租给你,你也没有吃亏,你看如何?” 张老汉一听觉得没有吃亏,就答应了 ,回到家中,他把这件事对邻居讲了,邻居一听,说:“张老汉你吃亏了!”,张老汉非常吃惊。
同学们,你能告诉张老汉这是为什么吗?小故事再见让我想想我能行利用平方差公式计算:
(2+1)(22+1)(24+1)(28+1)+1=(2-1)(2+1)(22+1)(24+1)(28+1)+1=(22-1)(22+1)(24+1)(28+1)+1=216
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
