浙教版七年级下册第一、二章综合复习(含解析)
文档属性
| 名称 | 浙教版七年级下册第一、二章综合复习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 403.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-31 19:53:53 | ||
图片预览



文档简介
浙教版七下第一、二章复习
一、选择题
1.下列现象中,不属于平移的是( )
A.铝合金窗户左右移动 B.钟摆的摆动
C.大楼中直上直下的电梯 D.火车在笔直的铁轨上飞驰而过
2.如图,直线a,b被直线c 所截,则∠1的同位角是 ( )
A.∠2 B.∠3 C.∠4 D.∠5
3.如果 是关于 x,y的二元一次方程,那么 ( )
A. B. C. D.
4. 如图,把一块含有30°角的三角尺的两个顶点放在直尺的对边上,如果∠1=22°,那么∠2的度数是( )
A.22° B.32° C.38° D.44°
5. 在关于x,y的二元一次方程组中,若2x+3y=2,则a的值为( )
A.2 B.3 C.4 D.-3
6.光线在不同介质中的传播速度是不同的,因此当光线从水中射向空气时,要发生折射,由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图,的度数为( )
A. B. C. D.
7.若关于x,y的二元一次方程组 的解为则方程组的解为 ( )
A. B. C. D.
8.《孙子算经》是中国古代重要的数学著作,成书大约在一千五百年前,其中一道题,原文是:“今三人共车,两车空;二人共车,九人步。问人与车各几何 ”意思是:现有若干人和车,若每辆车乘坐3人,则空余两辆车;若每辆车乘坐2人,则有9人步行,问人与车各多少?设有x人,y辆车,可列方程组为( )
A. B.
C. D.
9.我市为了方便市民绿色出行,推出了共享单车服务.图①是某品牌共享单车放在水平地面的实物图,图②是其示意图,其中AB,CD都与地面l平行,∠BCD=60°,∠BAC=50°,当∠MAC为( )度时,AM∥BE.
A.15 B.65 C.70 D.115
10.如图,已知,,点是射线上一动点(与点不重合),、分别平分和,分别交射线于点、,下列结论:①;②;③当时,;④当点运动时,的数量关系不变.其中正确结论有( )个.
A.1 B.2 C.3 D.4
二、填空题
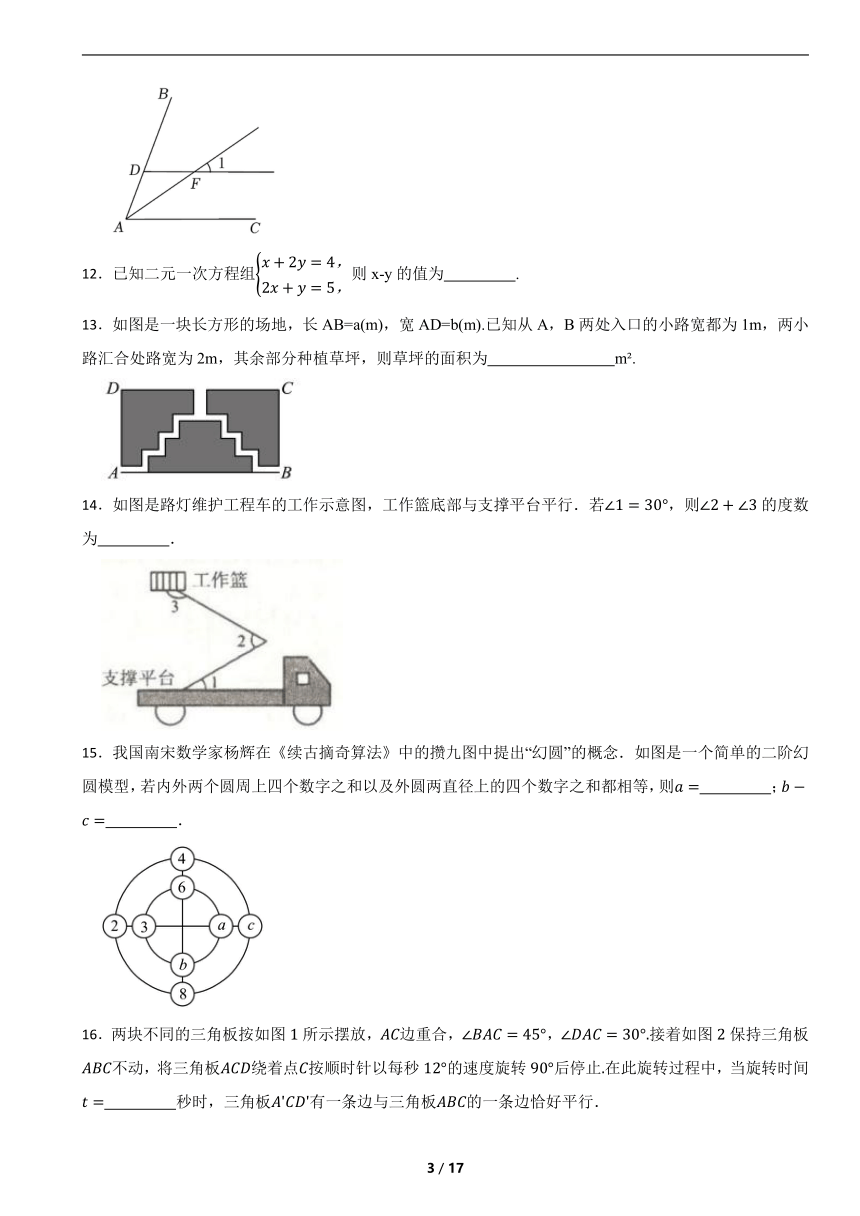
11.如图,AF是∠BAC的平分线,DF∥AC,若∠1=35°,则∠BAF的度数为 .
12.已知二元一次方程组则x-y的值为 .
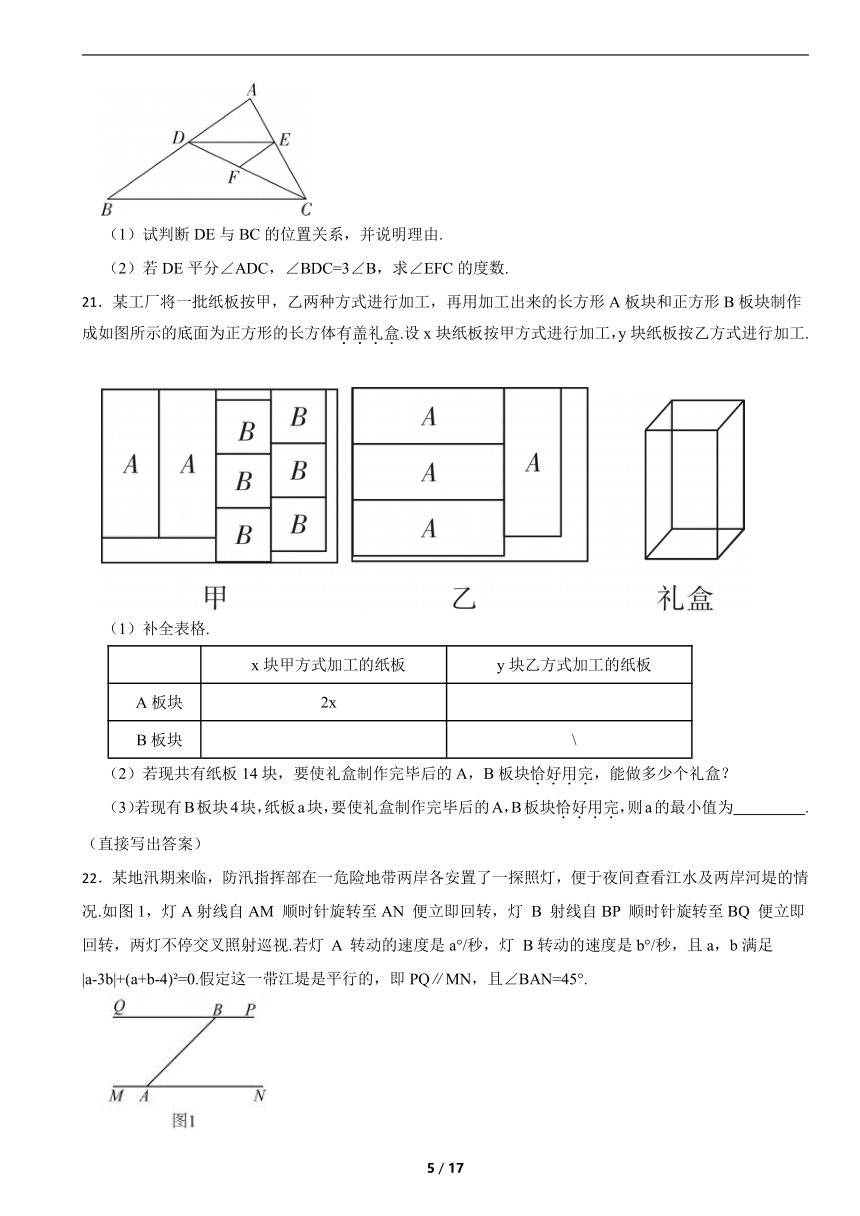
13.如图是一块长方形的场地,长AB=a(m),宽AD=b(m).已知从A,B两处入口的小路宽都为1m,两小路汇合处路宽为2m,其余部分种植草坪,则草坪的面积为 m .
14.如图是路灯维护工程车的工作示意图,工作篮底部与支撑平台平行.若,则的度数为 .
15.我国南宋数学家杨辉在《续古摘奇算法》中的攒九图中提出“幻圆”的概念.如图是一个简单的二阶幻圆模型,若内外两个圆周上四个数字之和以及外圆两直径上的四个数字之和都相等,则 ; .
16.两块不同的三角板按如图所示摆放,边重合,,接着如图保持三角板不动,将三角板绕着点按顺时针以每秒的速度旋转后停止在此旋转过程中,当旋转时间 秒时,三角板有一条边与三角板的一条边恰好平行.
三、解答题
17.解方程:
(1);
(2).
18.完成下面推理过程:
如图,已知:,、分别平分、.
求证:
证明:∵(已知)
∴ ▲ ( )
∵、分别平分、,(已知)
∴ ▲ , ▲ (角平分线定义)
∴( )
∴ ▲ ( )
∴( )
19.甲、乙两人共同解关于x,y的方程组 甲正确地解得乙看错了方程②中的系数c,解得 求 的值.
20.如图,已知∠EFC+∠BDC=180°,∠DEF=∠B.
(1)试判断DE与BC的位置关系,并说明理由.
(2)若DE平分∠ADC,∠BDC=3∠B,求∠EFC的度数.
21.某工厂将一批纸板按甲,乙两种方式进行加工,再用加工出来的长方形A板块和正方形B板块制作成如图所示的底面为正方形的长方体有盖礼盒.设x块纸板按甲方式进行加工,y块纸板按乙方式进行加工.
(1)补全表格.
x块甲方式加工的纸板 y块乙方式加工的纸板
A板块 2x
B板块
\
(2)若现共有纸板14块,要使礼盒制作完毕后的A,B板块恰好用完,能做多少个礼盒?
(3)若现有B板块4块,纸板a块,要使礼盒制作完毕后的A,B板块恰好用完,则a的最小值为 .(直接写出答案)
22.某地汛期来临,防汛指挥部在一危险地带两岸各安置了一探照灯,便于夜间查看江水及两岸河堤的情况.如图1,灯A射线自AM 顺时针旋转至AN 便立即回转,灯 B 射线自BP 顺时针旋转至BQ 便立即回转,两灯不停交叉照射巡视.若灯 A 转动的速度是a°/秒,灯 B转动的速度是b°/秒,且a,b满足|a-3b|+(a+b-4) =0.假定这一带江堤是平行的,即PQ∥MN,且∠BAN=45°.
(1)求a,b的值.
(2)若灯 B射线先转动30秒,灯A 射线才开始转动,在灯 B射线到达BQ 之前,灯 A 转动几秒,两灯的光束互相平行
(3)如图2,两灯同时转动,在灯 A 射线到达AN 之前,若两灯射出的光束相交于点C,过点C作CD⊥AC,交 PQ 于点 D,则在转动过程中,∠BCD:∠BAC的值是否发生变化 若不变,请求出该值;若改变,请求出其取值范围.
答案解析部分
1.【答案】B
【解析】【解答】解:A、铝合金窗户左右移动为平移现象,则本项不符合题意;
B、钟摆的摆动不为平移现象,则本项符合题意;
C、大楼中直上直下的电梯为平移现象,则本项不符合题意;
D、火车在笔直的铁轨上飞驰而过为平移现象,则本项不符合题意.
故答案为:B.
【分析】根据平移是不改变图形的形状、大小和方向,据此逐项分析即可.
2.【答案】D
【解析】【解答】解:由题意,∠1的同位角是∠5.
故答案为:D.
【分析】本题考查了同位角的定义.同位角的定义:两条直线a、b被第三条直线c所截,在截线c的同旁,且在被截两直线a、b的同一侧的一对角为同位角,根据同位角的定义进行判断即可.
3.【答案】C
【解析】【解答】解:∵是关于 x,y的二元一次方程,
∴
解得:
故答案为:C.
【分析】根据二元一次方程的定义:如果一个方程含有两个未知数,并且所含未知项都为1次方,那么这个整式方程就叫作二元一次方程,得到:即可求解.
4.【答案】C
【解析】【解答】解:如图所示:
由题可知:∠ABC=60°,,
,∠1=22°,
∠CBE=∠1=22°,
∠2=∠ABC-∠CBE=60°-22°=38°.
故答案为:C.
【分析】根据平行线的性质可得∠CBE=∠1=22°,再根据角的和差计算即可.
5.【答案】B
【解析】【解答】解:由得,
①-②×2得,2x+3y-2(x-2y)=2-2,
y=0,
把y=0代入②得,x=1,
把x=1,y=0代入3x+y=a得,
a=3.
故答案为:B.
【分析】把不含字母a的两个方程组成新的二元一次方程组,解出x,y的值,再把x,y的值代入关于a的方程,解方程即可.
6.【答案】B
【解析】【解答】解:如图所示:
根据题意得:,,
∴,,
∵,
∴.
故答案为:B
【分析】根据平行线的性质结合题意即可求解。
7.【答案】B
【解析】【解答】解: 化简得:,
∵二元一次方程组 的解为,
∴
∴
解得:,
故答案为:B.
【分析】将已知方程组化简得到,再结合已知方程组的解得到,进而即可求解.
8.【答案】C
【解析】【解答】解:设有x人,y辆车,依题意有:
,
故答案为:D.【分析】根据“每辆车乘坐3人,则空余两辆车;若每辆车乘坐2人,则有9人步行”,可得出两个等量关系式,由此可得出关于x,y的二元一次方程组,即可解答.
9.【答案】C
【解析】【解答】解:AB∥L,CD∥L,
AB∥CD,
∠BCD=∠ABC=60°,
∠BAC=50°,
∠ACB=180°-∠BAC-∠ABC=70°,
当∠MAC=∠ACB=70°时,AM∥BE.
故答案为:C.
【分析】根据平行线的性质可得∠BCD=∠ABC=60°,再利用三角形的内角和定理求得∠ACB=70°,最后根据两直线平行的判定定理即可求解.
10.【答案】D
【解析】【解答】解:∵,
∴,
故①符合题意;
∵,,
∴,
∵、分别平分和,
∴,,
∴,
故②符合题意;
∵,
∴,
又,
∴,
∴,
又,,
∴,
故③符合题意;
∵,
∴,,
又,
∴,
∴,
故④符合题意.
故答案为:D.
【分析】利用平行线的判定方法、平行线的性质及角的运算逐项判断即可。
11.【答案】35°
12.【答案】1
【解析】【解答】解:,
由①得③,
把③代入②得:,
解得:,
,
∴
故答案为:1.
【分析】利用代入消元法,解二元一次方程组,进而得出的值.
13.【答案】(ab-a-2b+2)
【解析】【解答】解:由图片可看出,种植草坪的面积正好可以拼成一个长方形,且这个长方形的长为(a-2)m,这个长方形的宽为(b-10)m,
∴草坪的面积为:(a-2)(b-1)=(ab-a-2b+2)m2.
故答案为:(ab-a-2b+2).
【分析】从图中可以看出,利用平移的方法,种植草坪的面积正好可以拼成一个长方形,然后根据题意求出长和宽,最后可求出面积.
14.【答案】
【解析】【解答】解:过顶点作直线l//支撑平台,
所以l//支撑平台//工作篮底部,
所以
所以
因为
所以
故答案为:.
【分析】过顶点作直线l//支撑平台,直线l将分成两个角,根据平行的性质即可求解。
15.【答案】;
【解析】【解答】解:由题意得:
化简得:
由②得:9+a=18
∴a=9
把a=9代入①得:14+c=18+b
∴b-c=14-18=-4
故答案为:9;-4.
【分析】由题意列出三元一次方程组并化简,观察第二个方程就可以求出a;把a代入第一个方程就可以求出b-c的值.
16.【答案】
【解析】【解答】解:由题意可知①当AB∥A'C时如图②,∠ACA’=45°,
∵△ACD绕着点C按顺时针方向以每秒12°的速度旋转,
∴t==,
∴此时t=
②当A'D∥AC时如图②,∠ACA'=30°,
∵△ACD绕着点C按顺时针方向以每秒12°的速度旋转,
∴t== ,
∴t=,
③如图
当A'D∥AB时,∠CEA'+∠ABC=180°,
∵∠ABC=90°,
∴∠CEA'=90°,
又∵∠CA'D=30°,
∴∠A'CE=60°,
∵∠ACB=45°,∠BCE=180°,
∴∠ACA'=75°,
∵△ACD绕着点C按顺时针方向以每秒12°的速度旋转,
∴ t = =,
∴此时 t=,
④如图
当AB∥CD'时,∠ABC=∠BCD'=90°,
∵∠ACD'=90°,
∵∠ACB=45°,
∴∠ACA'=135°,
∵△ACD绕着点C按顺时针方向以每秒12°的速度旋转,
∴ t==,
故答案为:、、或 .
【分析】此题分四种情况讨论:①当AB∥A'C时;②当A'D'∥AC时;③当A'D'∥AB;④AB∥CD时分别求出∠ACA'的度数,再除以每秒12°即可.
17.【答案】(1)解:,
①代入②得,
解得:,
把代入①,得;
解得:,
故方程组的解为:;
(2)解:,
方程组整理,得,
①②,得:,
解得:,
把代入①,得:,
解得:,
故方程组的解为:.
【解析】【分析】(1)将 ①代入 ②解得x的值,再将x的值代入任意式子即可解得y值,进而写出方程组的解;
(2)先将原式整理,然后利用加减消元解得y值,再将y值代入整理后的任意式子即可解得x值,进而写出原方程组的解.
18.【答案】ABC,两直线平行,同位角相等;ADE,ABC;等量代换;BE,同位角相等,两直线平行;两直线平行,内错角相等.
【解析】【解答】证明:∵(已知)
∴(两直线平行,同位角相等)
∵、分别平分、,
∴,(角平分线定义)
∴(等量代换)
∴(同位角相等,两直线平行)
∴(两直线平行,内错角相等).
故答案为:ABC,两直线平行,同位角相等;ADE,ABC;等量代换;BE,同位角相等,两直线平行;两直线平行,内错角相等.
【分析】由两直线平行,同位角相等,得∠ADE=∠ABC,由角平分线的定义及等量代换可得∠ADF=∠ABE,从而根据同位角相等,两直线平行可得DF∥BE,最后根据两直线平行,内错角相等,得出结论.
19.【答案】解:将与都代入方程组中的①方程,
得,
解得;
将代入方程组中的②方程,
得6-c=2,
解得c=4,
∴(a+b+c)2=(2-1+4)2=25.
【解析】【分析】将与都代入方程组中的①方程,可得关于字母a、b的方程组,求解得出a、b的值;再将代入方程组中的②方程,可求出c的值,最后将a、b、c的值代入待求式子按含乘方的有理数的混合运算的运算顺序计算即可.
20.【答案】(1)解:DE∥BC,理由如下:
∵∠EFC+∠DFE=180°,∠EFC+∠BDC=180°,
∴∠BDC=∠DFE,
∴AB∥EF,
∴∠DEF=∠ADE,
∵∠DEF=∠B,
∴∠B=∠ADE,
∴DE∥BC;
(2)解:∵DE∥BC,
∴∠ADE=∠B,
∵DE平分∠ADC,
∴∠ADC=2∠ADE=2∠B,
∵∠BDC=3∠B,∠BDC+∠ADC=180°,
∴5∠B=180°,
∴∠B=36°,
∴∠BDC=3∠B=108°,
∵ ∠EFC+∠BDC=180° ,
∴∠EFC=180°-∠BDC=72°.
【解析】【分析】(1)DE∥BC,理由如下:由邻补角和已知,根据同角的补角相等得∠BDC=∠DFE,由内错角相等,两直线平行,可得AB∥EF,再由二直线平行,内错角相等,得∠DEF=∠ADE,结合∠DEF=∠B,推出∠B=∠ADE,进而根据同位角相等,两直线平行可得DE∥BC;
(2)由二直线平行,同位角相等得∠ADE=∠B,由角平分线的定义得∠ADC=2∠ADE=2∠B,进而根据已知及平角定义可求出∠B=36°,∠BDC=3∠B=108°,∠EFC=180°-∠BDC=72°.
21.【答案】(1)解:
x块甲方式加工的纸板 y块乙方式加工的纸板
A板块
B板块 \
(2)解:由题意得, ,解得
礼盒: (个)
答:要使礼盒制作完毕后的A,B板块恰好用完,能做12个礼盒
(3)9
【解析】【解答】解:(1) 设x块甲方式加工的纸板, y块乙方式加工的纸板,
由甲图,按甲方式加工A板块2x快,B板块6x快;
由乙图,按甲方式加工A板块4y快;
故答案为:4y,6x.
(3)
解之:
∵x,a均为正整数,
∴
∴a的最小值为
故答案为:9.
【分析】(1)观察甲乙两图,由甲乙两种加工方式所裁剪的A,B板块的数量,可得答案.
(2)抓住关键已知条件:现共有纸板14块,要使礼盒制作完毕后的A,B板块恰好用完,可得到关于x,y的方程组,解方程组求出x,y的值,然后求出能做礼盒的数量.
(3)抓住关键已知条件:现有B板块4块,纸板a块,要使礼盒制作完毕后的A,B板块恰好用完;列出关于x,y,a的方程组,解方程组,用含a的代数式表示出x,y;根据x,a均为正整数,可得到a的最小值.
22.【答案】(1)解:∵
∴
∴
(2)解:设灯A转动t秒,两灯的光束互相平行,
①当时,
解得:
②当时,
解得:
③当时,
解得:,则舍去,
综上所述,灯A转动15秒或82.5秒时, 两灯的光束互相平
(3)解:不变,
设灯A转动t秒,
∵
∴
∵
∴
∵
∴
∴.
【解析】【分析】(1)根据非负数之和为0,则两个非负数均为0,据此即可求解;
(2)设灯A转动t秒,两灯的光束互相平行,分三种情况讨论,①当时,②当时,③当时,分别列出方程即可求解;
(3)设灯A转动t秒,用含t的式子表示出∠BAC和∠BCD,进而即可求解.
1 / 1
一、选择题
1.下列现象中,不属于平移的是( )
A.铝合金窗户左右移动 B.钟摆的摆动
C.大楼中直上直下的电梯 D.火车在笔直的铁轨上飞驰而过
2.如图,直线a,b被直线c 所截,则∠1的同位角是 ( )
A.∠2 B.∠3 C.∠4 D.∠5
3.如果 是关于 x,y的二元一次方程,那么 ( )
A. B. C. D.
4. 如图,把一块含有30°角的三角尺的两个顶点放在直尺的对边上,如果∠1=22°,那么∠2的度数是( )
A.22° B.32° C.38° D.44°
5. 在关于x,y的二元一次方程组中,若2x+3y=2,则a的值为( )
A.2 B.3 C.4 D.-3
6.光线在不同介质中的传播速度是不同的,因此当光线从水中射向空气时,要发生折射,由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图,的度数为( )
A. B. C. D.
7.若关于x,y的二元一次方程组 的解为则方程组的解为 ( )
A. B. C. D.
8.《孙子算经》是中国古代重要的数学著作,成书大约在一千五百年前,其中一道题,原文是:“今三人共车,两车空;二人共车,九人步。问人与车各几何 ”意思是:现有若干人和车,若每辆车乘坐3人,则空余两辆车;若每辆车乘坐2人,则有9人步行,问人与车各多少?设有x人,y辆车,可列方程组为( )
A. B.
C. D.
9.我市为了方便市民绿色出行,推出了共享单车服务.图①是某品牌共享单车放在水平地面的实物图,图②是其示意图,其中AB,CD都与地面l平行,∠BCD=60°,∠BAC=50°,当∠MAC为( )度时,AM∥BE.
A.15 B.65 C.70 D.115
10.如图,已知,,点是射线上一动点(与点不重合),、分别平分和,分别交射线于点、,下列结论:①;②;③当时,;④当点运动时,的数量关系不变.其中正确结论有( )个.
A.1 B.2 C.3 D.4
二、填空题
11.如图,AF是∠BAC的平分线,DF∥AC,若∠1=35°,则∠BAF的度数为 .
12.已知二元一次方程组则x-y的值为 .
13.如图是一块长方形的场地,长AB=a(m),宽AD=b(m).已知从A,B两处入口的小路宽都为1m,两小路汇合处路宽为2m,其余部分种植草坪,则草坪的面积为 m .
14.如图是路灯维护工程车的工作示意图,工作篮底部与支撑平台平行.若,则的度数为 .
15.我国南宋数学家杨辉在《续古摘奇算法》中的攒九图中提出“幻圆”的概念.如图是一个简单的二阶幻圆模型,若内外两个圆周上四个数字之和以及外圆两直径上的四个数字之和都相等,则 ; .
16.两块不同的三角板按如图所示摆放,边重合,,接着如图保持三角板不动,将三角板绕着点按顺时针以每秒的速度旋转后停止在此旋转过程中,当旋转时间 秒时,三角板有一条边与三角板的一条边恰好平行.
三、解答题
17.解方程:
(1);
(2).
18.完成下面推理过程:
如图,已知:,、分别平分、.
求证:
证明:∵(已知)
∴ ▲ ( )
∵、分别平分、,(已知)
∴ ▲ , ▲ (角平分线定义)
∴( )
∴ ▲ ( )
∴( )
19.甲、乙两人共同解关于x,y的方程组 甲正确地解得乙看错了方程②中的系数c,解得 求 的值.
20.如图,已知∠EFC+∠BDC=180°,∠DEF=∠B.
(1)试判断DE与BC的位置关系,并说明理由.
(2)若DE平分∠ADC,∠BDC=3∠B,求∠EFC的度数.
21.某工厂将一批纸板按甲,乙两种方式进行加工,再用加工出来的长方形A板块和正方形B板块制作成如图所示的底面为正方形的长方体有盖礼盒.设x块纸板按甲方式进行加工,y块纸板按乙方式进行加工.
(1)补全表格.
x块甲方式加工的纸板 y块乙方式加工的纸板
A板块 2x
B板块
\
(2)若现共有纸板14块,要使礼盒制作完毕后的A,B板块恰好用完,能做多少个礼盒?
(3)若现有B板块4块,纸板a块,要使礼盒制作完毕后的A,B板块恰好用完,则a的最小值为 .(直接写出答案)
22.某地汛期来临,防汛指挥部在一危险地带两岸各安置了一探照灯,便于夜间查看江水及两岸河堤的情况.如图1,灯A射线自AM 顺时针旋转至AN 便立即回转,灯 B 射线自BP 顺时针旋转至BQ 便立即回转,两灯不停交叉照射巡视.若灯 A 转动的速度是a°/秒,灯 B转动的速度是b°/秒,且a,b满足|a-3b|+(a+b-4) =0.假定这一带江堤是平行的,即PQ∥MN,且∠BAN=45°.
(1)求a,b的值.
(2)若灯 B射线先转动30秒,灯A 射线才开始转动,在灯 B射线到达BQ 之前,灯 A 转动几秒,两灯的光束互相平行
(3)如图2,两灯同时转动,在灯 A 射线到达AN 之前,若两灯射出的光束相交于点C,过点C作CD⊥AC,交 PQ 于点 D,则在转动过程中,∠BCD:∠BAC的值是否发生变化 若不变,请求出该值;若改变,请求出其取值范围.
答案解析部分
1.【答案】B
【解析】【解答】解:A、铝合金窗户左右移动为平移现象,则本项不符合题意;
B、钟摆的摆动不为平移现象,则本项符合题意;
C、大楼中直上直下的电梯为平移现象,则本项不符合题意;
D、火车在笔直的铁轨上飞驰而过为平移现象,则本项不符合题意.
故答案为:B.
【分析】根据平移是不改变图形的形状、大小和方向,据此逐项分析即可.
2.【答案】D
【解析】【解答】解:由题意,∠1的同位角是∠5.
故答案为:D.
【分析】本题考查了同位角的定义.同位角的定义:两条直线a、b被第三条直线c所截,在截线c的同旁,且在被截两直线a、b的同一侧的一对角为同位角,根据同位角的定义进行判断即可.
3.【答案】C
【解析】【解答】解:∵是关于 x,y的二元一次方程,
∴
解得:
故答案为:C.
【分析】根据二元一次方程的定义:如果一个方程含有两个未知数,并且所含未知项都为1次方,那么这个整式方程就叫作二元一次方程,得到:即可求解.
4.【答案】C
【解析】【解答】解:如图所示:
由题可知:∠ABC=60°,,
,∠1=22°,
∠CBE=∠1=22°,
∠2=∠ABC-∠CBE=60°-22°=38°.
故答案为:C.
【分析】根据平行线的性质可得∠CBE=∠1=22°,再根据角的和差计算即可.
5.【答案】B
【解析】【解答】解:由得,
①-②×2得,2x+3y-2(x-2y)=2-2,
y=0,
把y=0代入②得,x=1,
把x=1,y=0代入3x+y=a得,
a=3.
故答案为:B.
【分析】把不含字母a的两个方程组成新的二元一次方程组,解出x,y的值,再把x,y的值代入关于a的方程,解方程即可.
6.【答案】B
【解析】【解答】解:如图所示:
根据题意得:,,
∴,,
∵,
∴.
故答案为:B
【分析】根据平行线的性质结合题意即可求解。
7.【答案】B
【解析】【解答】解: 化简得:,
∵二元一次方程组 的解为,
∴
∴
解得:,
故答案为:B.
【分析】将已知方程组化简得到,再结合已知方程组的解得到,进而即可求解.
8.【答案】C
【解析】【解答】解:设有x人,y辆车,依题意有:
,
故答案为:D.【分析】根据“每辆车乘坐3人,则空余两辆车;若每辆车乘坐2人,则有9人步行”,可得出两个等量关系式,由此可得出关于x,y的二元一次方程组,即可解答.
9.【答案】C
【解析】【解答】解:AB∥L,CD∥L,
AB∥CD,
∠BCD=∠ABC=60°,
∠BAC=50°,
∠ACB=180°-∠BAC-∠ABC=70°,
当∠MAC=∠ACB=70°时,AM∥BE.
故答案为:C.
【分析】根据平行线的性质可得∠BCD=∠ABC=60°,再利用三角形的内角和定理求得∠ACB=70°,最后根据两直线平行的判定定理即可求解.
10.【答案】D
【解析】【解答】解:∵,
∴,
故①符合题意;
∵,,
∴,
∵、分别平分和,
∴,,
∴,
故②符合题意;
∵,
∴,
又,
∴,
∴,
又,,
∴,
故③符合题意;
∵,
∴,,
又,
∴,
∴,
故④符合题意.
故答案为:D.
【分析】利用平行线的判定方法、平行线的性质及角的运算逐项判断即可。
11.【答案】35°
12.【答案】1
【解析】【解答】解:,
由①得③,
把③代入②得:,
解得:,
,
∴
故答案为:1.
【分析】利用代入消元法,解二元一次方程组,进而得出的值.
13.【答案】(ab-a-2b+2)
【解析】【解答】解:由图片可看出,种植草坪的面积正好可以拼成一个长方形,且这个长方形的长为(a-2)m,这个长方形的宽为(b-10)m,
∴草坪的面积为:(a-2)(b-1)=(ab-a-2b+2)m2.
故答案为:(ab-a-2b+2).
【分析】从图中可以看出,利用平移的方法,种植草坪的面积正好可以拼成一个长方形,然后根据题意求出长和宽,最后可求出面积.
14.【答案】
【解析】【解答】解:过顶点作直线l//支撑平台,
所以l//支撑平台//工作篮底部,
所以
所以
因为
所以
故答案为:.
【分析】过顶点作直线l//支撑平台,直线l将分成两个角,根据平行的性质即可求解。
15.【答案】;
【解析】【解答】解:由题意得:
化简得:
由②得:9+a=18
∴a=9
把a=9代入①得:14+c=18+b
∴b-c=14-18=-4
故答案为:9;-4.
【分析】由题意列出三元一次方程组并化简,观察第二个方程就可以求出a;把a代入第一个方程就可以求出b-c的值.
16.【答案】
【解析】【解答】解:由题意可知①当AB∥A'C时如图②,∠ACA’=45°,
∵△ACD绕着点C按顺时针方向以每秒12°的速度旋转,
∴t==,
∴此时t=
②当A'D∥AC时如图②,∠ACA'=30°,
∵△ACD绕着点C按顺时针方向以每秒12°的速度旋转,
∴t== ,
∴t=,
③如图
当A'D∥AB时,∠CEA'+∠ABC=180°,
∵∠ABC=90°,
∴∠CEA'=90°,
又∵∠CA'D=30°,
∴∠A'CE=60°,
∵∠ACB=45°,∠BCE=180°,
∴∠ACA'=75°,
∵△ACD绕着点C按顺时针方向以每秒12°的速度旋转,
∴ t = =,
∴此时 t=,
④如图
当AB∥CD'时,∠ABC=∠BCD'=90°,
∵∠ACD'=90°,
∵∠ACB=45°,
∴∠ACA'=135°,
∵△ACD绕着点C按顺时针方向以每秒12°的速度旋转,
∴ t==,
故答案为:、、或 .
【分析】此题分四种情况讨论:①当AB∥A'C时;②当A'D'∥AC时;③当A'D'∥AB;④AB∥CD时分别求出∠ACA'的度数,再除以每秒12°即可.
17.【答案】(1)解:,
①代入②得,
解得:,
把代入①,得;
解得:,
故方程组的解为:;
(2)解:,
方程组整理,得,
①②,得:,
解得:,
把代入①,得:,
解得:,
故方程组的解为:.
【解析】【分析】(1)将 ①代入 ②解得x的值,再将x的值代入任意式子即可解得y值,进而写出方程组的解;
(2)先将原式整理,然后利用加减消元解得y值,再将y值代入整理后的任意式子即可解得x值,进而写出原方程组的解.
18.【答案】ABC,两直线平行,同位角相等;ADE,ABC;等量代换;BE,同位角相等,两直线平行;两直线平行,内错角相等.
【解析】【解答】证明:∵(已知)
∴(两直线平行,同位角相等)
∵、分别平分、,
∴,(角平分线定义)
∴(等量代换)
∴(同位角相等,两直线平行)
∴(两直线平行,内错角相等).
故答案为:ABC,两直线平行,同位角相等;ADE,ABC;等量代换;BE,同位角相等,两直线平行;两直线平行,内错角相等.
【分析】由两直线平行,同位角相等,得∠ADE=∠ABC,由角平分线的定义及等量代换可得∠ADF=∠ABE,从而根据同位角相等,两直线平行可得DF∥BE,最后根据两直线平行,内错角相等,得出结论.
19.【答案】解:将与都代入方程组中的①方程,
得,
解得;
将代入方程组中的②方程,
得6-c=2,
解得c=4,
∴(a+b+c)2=(2-1+4)2=25.
【解析】【分析】将与都代入方程组中的①方程,可得关于字母a、b的方程组,求解得出a、b的值;再将代入方程组中的②方程,可求出c的值,最后将a、b、c的值代入待求式子按含乘方的有理数的混合运算的运算顺序计算即可.
20.【答案】(1)解:DE∥BC,理由如下:
∵∠EFC+∠DFE=180°,∠EFC+∠BDC=180°,
∴∠BDC=∠DFE,
∴AB∥EF,
∴∠DEF=∠ADE,
∵∠DEF=∠B,
∴∠B=∠ADE,
∴DE∥BC;
(2)解:∵DE∥BC,
∴∠ADE=∠B,
∵DE平分∠ADC,
∴∠ADC=2∠ADE=2∠B,
∵∠BDC=3∠B,∠BDC+∠ADC=180°,
∴5∠B=180°,
∴∠B=36°,
∴∠BDC=3∠B=108°,
∵ ∠EFC+∠BDC=180° ,
∴∠EFC=180°-∠BDC=72°.
【解析】【分析】(1)DE∥BC,理由如下:由邻补角和已知,根据同角的补角相等得∠BDC=∠DFE,由内错角相等,两直线平行,可得AB∥EF,再由二直线平行,内错角相等,得∠DEF=∠ADE,结合∠DEF=∠B,推出∠B=∠ADE,进而根据同位角相等,两直线平行可得DE∥BC;
(2)由二直线平行,同位角相等得∠ADE=∠B,由角平分线的定义得∠ADC=2∠ADE=2∠B,进而根据已知及平角定义可求出∠B=36°,∠BDC=3∠B=108°,∠EFC=180°-∠BDC=72°.
21.【答案】(1)解:
x块甲方式加工的纸板 y块乙方式加工的纸板
A板块
B板块 \
(2)解:由题意得, ,解得
礼盒: (个)
答:要使礼盒制作完毕后的A,B板块恰好用完,能做12个礼盒
(3)9
【解析】【解答】解:(1) 设x块甲方式加工的纸板, y块乙方式加工的纸板,
由甲图,按甲方式加工A板块2x快,B板块6x快;
由乙图,按甲方式加工A板块4y快;
故答案为:4y,6x.
(3)
解之:
∵x,a均为正整数,
∴
∴a的最小值为
故答案为:9.
【分析】(1)观察甲乙两图,由甲乙两种加工方式所裁剪的A,B板块的数量,可得答案.
(2)抓住关键已知条件:现共有纸板14块,要使礼盒制作完毕后的A,B板块恰好用完,可得到关于x,y的方程组,解方程组求出x,y的值,然后求出能做礼盒的数量.
(3)抓住关键已知条件:现有B板块4块,纸板a块,要使礼盒制作完毕后的A,B板块恰好用完;列出关于x,y,a的方程组,解方程组,用含a的代数式表示出x,y;根据x,a均为正整数,可得到a的最小值.
22.【答案】(1)解:∵
∴
∴
(2)解:设灯A转动t秒,两灯的光束互相平行,
①当时,
解得:
②当时,
解得:
③当时,
解得:,则舍去,
综上所述,灯A转动15秒或82.5秒时, 两灯的光束互相平
(3)解:不变,
设灯A转动t秒,
∵
∴
∵
∴
∵
∴
∴.
【解析】【分析】(1)根据非负数之和为0,则两个非负数均为0,据此即可求解;
(2)设灯A转动t秒,两灯的光束互相平行,分三种情况讨论,①当时,②当时,③当时,分别列出方程即可求解;
(3)设灯A转动t秒,用含t的式子表示出∠BAC和∠BCD,进而即可求解.
1 / 1
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
