浙教版七年级下册第三章 整式的乘除 单元检测卷(含解析)
文档属性
| 名称 | 浙教版七年级下册第三章 整式的乘除 单元检测卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 67.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-31 23:10:20 | ||
图片预览




文档简介
浙教版第三章整式的乘除单元检测卷
一、选择题
1. 下列运算正确的是( )
A. B. C. D.
2.已知,则的值是( )
A.1 B.2 C.3 D.4
3.下列计算正确的是( )
A. B.
C. D.
4.下列各式中,不能使用平方差公式计算的是( )
A.(2a+3b)(2a-3b) B.(-2a+3b)(3b-2a)
C.(-2a+3b)(-2a-3b) D.(2a-3b)(-2a-3b)
5.如果长方形的长为(4a2-2a+1),宽为(2a+1),则这个长方形的面积为( )
A.8a3-4a2+2a-1 B.8a3+4a2-2a-1
C.8a3-1 D.8a3+1
6.如图,从边长为的正方形纸片中剪去一个边长为的正方形,剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙),则该矩形的面积是( )
A. B. C. D.
7.如图为2024年某月日历,现用一个正方形方框框住部分(阴影部分)9个位置上的数,若最小的数与最大的数的积记为n,中间位置上的数记为m.下列所给的数据中,n不可能是( )
A.377 B.420 C.465 D.512
8.如图,把一块面积为100的大长方形木板被分割成2个大小一样的大正方形①,1个小正方形②和2个大小一样的长方形③后,如图摆放,且每个小长方形③的面积为16,则标号为②的正方形的面积是( )
A.16 B.14 C.12 D.10
9.(2+1)(22+1)(24+1)…(216+1)的结果为( )
A.232-1 B.232+1 C.232 D.216
10.我国宋代数学家杨辉发现了(,1,2,3,…)展开式系数的规律:
以上系数三角表称为“杨辉三角”,根据上述规律,展开式的系数和是( )
A.64 B.128 C.256 D.612
二、填空题
11.计算: .
12.已知,,则 .
13.若满足,则整数的值为 .
14.已知的展开式中不含和项,则 .
15.若,则 .
16.如图,把三个大小相同的正方形甲,乙,丙放在边长为9的大正方形中,甲与丙的重叠部分面积记为S1,乙与丙的重叠部分面积记为S2,且均为正方形,正方形甲、乙一组邻边的延长线构成的正方形面积记为S3,若S1-S2=2S3,且S3=1,则图中阴影部分的面积为 .
三、解答题
17.规定,求:
(1)求;
(2)若,求x的值.
18.先化简后求值:,其中a,b满足.
19.小马和小虎两人共同计算一道整式乘法题:,由于小马抄错了的符号,得到的结果为;由于小虎漏抄了第一个多项式中的系数,得到的结果为.
(1)求出,的值;
(2)请你计算出这道整式乘法题的正确结果.
20.图1是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀剪下全等的四块小长方形,然后按图2拼成一个正方形.
图1 图2
(1)直接写出图2中阴影部分的正方形的边长为
(2)观察图2,请直接写出下列三个代数式(m+n) 2,(m- n) 2,mn之间的等量关系是
(3)根据(2)中的等量关系,解决如下问题:
①若 p+q=9,pq=7,求(p- q) 2的值:
②若(2021- a) 2+( a - 2022) 2=7,求(2021- a) ( a- 2022)的值.
21.若x满足(9-x)(x-4)=4,求的值.
解:设9-x=a,x-4=b,则(9-x)(x-4)=ab=4,a+b=(9-x)+(x-4)=5,
请仿照上面的方法解答下面的问题:
(1)若x满足(x-10)(x-20)=15,求的值.
(2)若x满足(求(x-2023)(x-2024)的值.
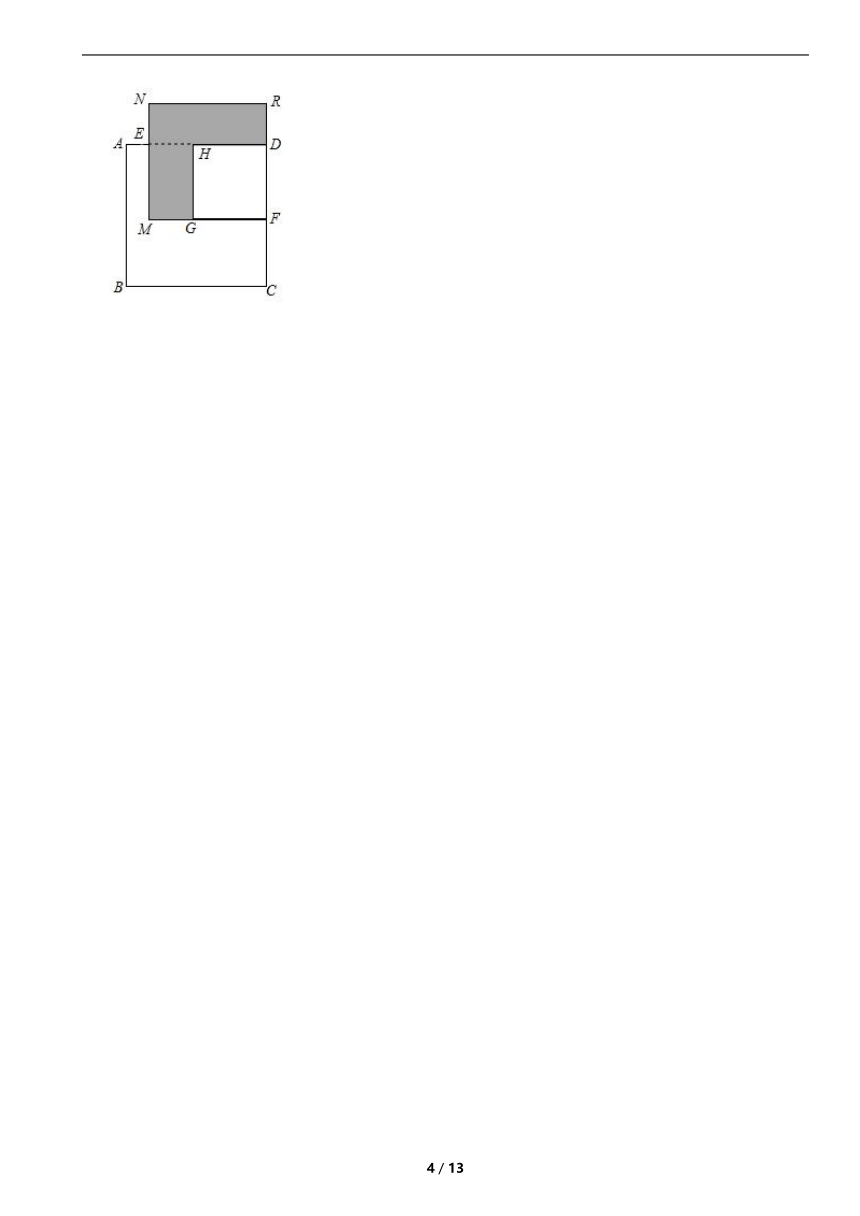
(3)如图,已知正方形ABCD的边长为x,E,F分别是AD,DC上的点,且AE=1,CF=3,长方形EMFD的面积是48,分别以MF,DF为边长作正方形MFRN和正方形GFDH,求阴影部分的面积.
答案解析部分
1.【答案】C
【解析】【解答】解:A.与a不是同类项,不能合并,A不符合题意;
B.同底数幂相乘,底数不变,指数相加,,B不符合题意;
C.,C符合题意;
D.同底数幂相除,底数不变,指数相减,,D不符合题意;
故答案为:C.
【分析】根据同底数幂乘除法、积的乘方,同类项相加结合题意对选项逐一分析即可求解。
2.【答案】C
3.【答案】D
【解析】【解答】解:A、,A不符合题意;
B、,B不符合题意;
C、,C不符合题意;
D、,D符合题意;
故答案为:D
【分析】根据完全平方公式、平方差公式结合题意对选项逐一分析即可求解。
4.【答案】B
【解析】【解答】解:A、 (2a+3b)(2a-3b) ,符合平方差公式的结构特点,能用平方差公式计算,故此选项不符合题意;
B、 (-2a+3b)(3b-2a) =(-2a+3b)(-2a+3b) ,不符合平方差公式的结构特点,不能用平方差公式计算,故此选项符合题意;
C、 (-2a+3b)(-2a-3b) ,符合平方差公式的结构特点,能用平方差公式计算,故此选项不符合题意;
D、 (2a-3b)(-2a-3b)=(-3b+2a)(-3b-2a) ,符合平方差公式的结构特点,能用平方差公式计算,故此选项不符合题意.
故答案为:B.
【分析】两个二项式相乘,如果这两个二项式中满足:有一项完全相同,另一项只有符号不同,那么这样的两个二项式相乘,就可以使用平方差公式进行计算,据此逐项判断得出答案.
5.【答案】D
【解析】【解答】解:这个长方形的面积为 (4a2-2a+1)(2a+1)=4a2·(2a+1)-2a(2a+1)+2a+1
= 8a3+1 .
故答案为:D.
【分析】根据长方形的面积=长×宽先列式,再计算即可.
6.【答案】C
7.【答案】D
【解析】【解答】解:最大和最小的两个数是m+8和m-8,
∴n=(m-8)(m+8)=m2-64,
即m2=64+n;
A、当n=377时, 64+377=441=212 ,结果是一个平方数,所以n可能是377,A不符合题意;
B、当n=420时,420+64=484=222,结果是一个平方数,所以n可能是420,B不符合题意;
C、当n=465时,465+64=529=232,结果是一个平方数,所以n可能是465,C不符合题意;
D、当n=512时,512+64=576=242,最小的数是24-8=16,最大的数是24+8=32,不符合实际,D符合题意;
故答案为:D.
【分析】先用含有m的式子表示出最大和最小的两个数,结合题意可得m2=64+n,逐项将n的值代入,判断是否是平方数,注意结合实际,即可判断得出答案.
8.【答案】C
【解析】【解答】解:设正方形①的边长为a,正方形②的边长为b,
∴长方形③的长=a+b,宽=a-b,
∵长方形③的面积为16,
∴(a+b)(a-b)=16,
∴a2-b2=16(1)
∵大长方形的长=2a+b,大长方形的宽=2a-b,
∵大长方形的面积为100,
∴(2a+b)(2a-b)=100,
∴4a2-b2=100(2)
由(2)-(1)×4,得:3b2=36,
∴b2=12,
∴正方形②的面积=b2=12.
故答案为:C.
【分析】设正方形①边长为a,正方形②边长为b,表示出长方形③长=a+b,宽=a-b,由长方形③面积为16,可得(a+b)(a-b)=16,整理得a2-b2=16(1);大长方形长=2a+b,大长方形宽=2a-b,由大长方形面积为100,可得(2a+b)(2a-b)=100,整理得4a2-b2=100(2),再由(2)-(1)×4,得3b2=36,解得b2=12,即可正方形②的面积.
9.【答案】A
【解析】【解答】解:原式=(2-1)(2+1)(22+1)(24+1)…(216+1)
=(22-1)(22+1)(24+1)…(216+1)
=(24-1)(24+1)…(216+1)
=(28-1)…(216+1)
=232-1,
故答案为:A.
【分析】将原式变形为(2-1)(2+1)(22+1)(24+1)…(216+1),然后利用平方差公式计算即可.
10.【答案】C
【解析】【解答】解:由“杨辉三角”的规律可知,
展开式中所有项的系数和为1,
展开式中所有项的系数和为2,
展开式中所有项的系数和为4,
展开式中所有项的系数和为8,
……
展开式中所有项的系数和为,
展开式中所有项的系数和为.
故答案为:C.
【分析】先计算n=0,1,2,3,时,展开式中所有项的系数和,从中得出规律为展开式中所有项的系数和为,再把n=8代入计算即可。
11.【答案】
【解析】【解答】解:原式=,
故答案为:
【分析】根据积的乘方法则,幂的乘方法则,同底数幂的除法法则计算即可.
12.【答案】-1
13.【答案】 或 3 或 1
【解析】【解答】解:由题意得:
①x+1=0,
解得:x=﹣1;
②x﹣2=1,
解得:x=3;
③x﹣2=﹣1,x+1为偶数,
解得:x=1,
故答案为:﹣1或3或1.
【分析】由 知,要分三种情况讨论,即:根据零指数幂可得x+1=0,根据有理数的乘方可得x﹣2=1;x﹣2=﹣1,x+1为偶数,再解方程即可解答.
14.【答案】10
【解析】【解答】解:
∴m-3=0,2-3m+n=0
∴m=3,n=7
∴m+n=10
故答案为:10.
【分析】本题考查整式乘法的计算方法,熟知整式乘法中多项式乘以多项式计算法则是解题关键,根据多项式乘以多项式计算法则展开合并,结合展开式中不含,可得m-3=0,2-3m+n=0解得m,n的值,即可得出答案.
15.【答案】或
【解析】【解答】解:∵a3+3a2+a=a(a2+3a+1)=0,
∴a=0或a2+3a+1=0,
当a=0时,;
当a2+3a+1=0时,,
∴,
∴,
∴,
∴,
综上,的值为0或.
故答案为:0或.
【分析】先将已知方程的左边利用提取公因式法分解因式,进而根据两个因式的乘积等于零,则至少有一个因式为零,从而得出a=0或a2+3a+1=0,从而分两种情况求值;当a=0时易得所求式子的 值为零;当a2+3a+1=0时,等式的两边同时除以a得,再将该式两边同时平方得,进而可求出待求式子的倒数,即可解决此题.
16.【答案】
【解析】【解答】解:设正方形甲、乙、丙的边长为a,
∵正方形甲、乙一组邻边的延长线构成的正方形面积记为S3,且S3=1,大正方形边长为9,
∴2a+1=9,
∴a=4,
设正方形S1,S2的边长分别为x,y,
∴x+y+1=4,即x+y=3①,
又∵S1-S2=2S3,
∴x2-y2=2,即(x+y)(x-y)=2,
∴(x-y)=②,
由①得:x2+2xy+y2=9,
由②得:x2-2xy+y2=,
∴4xy=,
∴xy=,
∴S阴影=(x+1)(y+1)-S3=xy+x+y+1-1,
∴S阴影=+3=.
故答案为:.
【分析】设正方形甲、乙、丙的边长为a,由正方形甲、乙一组邻边延长线构成的正方形面积记为S3,且S3=1,大正方形边长为9,推出2a+1=9,解得a=4,设正方形S1,S2的边长分别为x,y,从而得到x+y+1=4,即x+y=3①,再由S1-S2=2S3,得x2-y2=2,利用平方差公式可求得(x-y)=②,再利用完全平方公式得x2+2xy+y2=9,x2-2xy+y2=,则4xy=,即得xy=,最后根据阴影部分正方形的面积(x+1)(y+1)-S3=xy+x+y+1-1,代入数据计算即可求解.
17.【答案】(1)解:由题意得:;
(2)解:∵,
∴,
∴,
∴,
∴
【解析】【分析】(1)根据新运算,结合同底数幂的乘法即可求出答案.
(2)根据新运算,结合同底数幂的乘法即可求出答案.
18.【答案】解:
,
,
,,
,,
,,
原式.
【解析】【分析】先利用整式的混合运算化简,再利用非负数之和为0的性质求出a、b的值,最后将a、b的值代入计算即可.
19.【答案】(1)解:
由于小马抄错了的符号,得到的结果为:
;
①,
小虎漏抄了第一个多项式中的系数,
得到的结果为,
②,
由①②解得;
故,;
(2)解:由(1)得
;
故这道整式乘法题的正确结果为.
【解析】【分析】(1)根据 小马抄错了的符号,可以进行: ,得出结果为 :,进而可得出 ①;然后再根据小虎漏抄了第一个多项式中的系数,得到的结果为 ,可得出 ②, 联立①②,解方程组,即可得出 ,;
(2)把,代入原式,然后再正确进行计算即可。
20.【答案】(1)m-n
(2)故答案为:(m- n) 2 =(m+n) 2- 4mn;
(3)解:①由(2)可知,
(p - q) 2 = (p +q) 2–4pq
= 81-28
= 53;
②设x=2021-a,y=a-2022,则x+y=-1,x2+y2=7,
∵(x+y) 2= 1
∴x2 + 2xy+y2= 1
2xy= -6
xy= -3
∴(2021- a)(a - 2022)的值为-3.
【解析】【解答】解:(1)图2中的阴影部分的正方形的边长等于.
故答案为:,
(2)由题意得:小正方形面积等于大正方形的面积减去4个长方形的面积,即,阴影部分正方形的面积为,
所以,
故答案为:(m- n) 2 =(m+n) 2- 4mn;
【分析】(1)观察得到阴影部分的正方形的边长等与长为m,宽为n的长方形的长宽之差;
(2)小正方形面积等于大正方形的面积减去4个长方形的面积,即,阴影部分正方形的面积为,根据等面积法即可求解.
(3)①根据(2)的等量关系进行计算即可求解;
②设x=2021-a,y=a-2022,则x+y=-1,x2+y2=7,可推出xy= -3,即可得解.
21.【答案】(1)解:设x-10=a,x-20=b,
则 (x-10)(x-20)=ab=15, (x-10)-(x-20)=a-b=10,
∴(x-10)2+(x-20)2=a2+b2=(a-b)2+2ab=102+2×15=130.
(2)解:设x-2023=a,x-2024=b,
则 (x-2023)2+(x-2024)2=a2+b2=33, (x-2023)-(x-2024)=a-b=1,
∴(a-b)2=12,
∴a2-2ab+b2=1,
∴33-2ab=1,解得:ab=16,
故(x-2023)(x-2024)=ab=16.
(3)解:∵正方形的边长为x,AE=1,CF=3,
∴FM=DE=x-1,DF=x-3,
∴(x-1)(x-3)=48,
∴(x-1)-(x-3)=2,
∴阴影部分的面积=FM2-DF2=(x-1)2-(x-3)2,
设x-1=a,x-3=b,则(x-1)(x-3)=ab=48,a-b=(x-1)-(x-3)=2,
∴(a+b)2=(a-b)2+4ab=4+192=196,
∵a>0,b>0,
∴a+b>0,
∴a+b=14,
∴(x-1)2-(x-3)2
=a2-b2
=(a+b)(a-b)
=14×2=28.
即阴影部分的面积为28.
【解析】【分析】(1)设x-2023=a,x-2024=b,由已知条件得ab=1,a-b=10,根据a2+b2=(a-b)2+2ab即可求解;
(2)设x-2023=a,x-2024=b,结合已知可得a2+b2=33,a-b=2,将a-b=2两边分别平方,然后整体代换即可求解;
(3)观察图形,根据线段的构成将FM=DE,DF用含x的代数式表示出来,根据阴影部分的面积=FM2-DF2=(x-1)2-(x-3)2,根据(2)的方法计算即可求解.
1 / 1
一、选择题
1. 下列运算正确的是( )
A. B. C. D.
2.已知,则的值是( )
A.1 B.2 C.3 D.4
3.下列计算正确的是( )
A. B.
C. D.
4.下列各式中,不能使用平方差公式计算的是( )
A.(2a+3b)(2a-3b) B.(-2a+3b)(3b-2a)
C.(-2a+3b)(-2a-3b) D.(2a-3b)(-2a-3b)
5.如果长方形的长为(4a2-2a+1),宽为(2a+1),则这个长方形的面积为( )
A.8a3-4a2+2a-1 B.8a3+4a2-2a-1
C.8a3-1 D.8a3+1
6.如图,从边长为的正方形纸片中剪去一个边长为的正方形,剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙),则该矩形的面积是( )
A. B. C. D.
7.如图为2024年某月日历,现用一个正方形方框框住部分(阴影部分)9个位置上的数,若最小的数与最大的数的积记为n,中间位置上的数记为m.下列所给的数据中,n不可能是( )
A.377 B.420 C.465 D.512
8.如图,把一块面积为100的大长方形木板被分割成2个大小一样的大正方形①,1个小正方形②和2个大小一样的长方形③后,如图摆放,且每个小长方形③的面积为16,则标号为②的正方形的面积是( )
A.16 B.14 C.12 D.10
9.(2+1)(22+1)(24+1)…(216+1)的结果为( )
A.232-1 B.232+1 C.232 D.216
10.我国宋代数学家杨辉发现了(,1,2,3,…)展开式系数的规律:
以上系数三角表称为“杨辉三角”,根据上述规律,展开式的系数和是( )
A.64 B.128 C.256 D.612
二、填空题
11.计算: .
12.已知,,则 .
13.若满足,则整数的值为 .
14.已知的展开式中不含和项,则 .
15.若,则 .
16.如图,把三个大小相同的正方形甲,乙,丙放在边长为9的大正方形中,甲与丙的重叠部分面积记为S1,乙与丙的重叠部分面积记为S2,且均为正方形,正方形甲、乙一组邻边的延长线构成的正方形面积记为S3,若S1-S2=2S3,且S3=1,则图中阴影部分的面积为 .
三、解答题
17.规定,求:
(1)求;
(2)若,求x的值.
18.先化简后求值:,其中a,b满足.
19.小马和小虎两人共同计算一道整式乘法题:,由于小马抄错了的符号,得到的结果为;由于小虎漏抄了第一个多项式中的系数,得到的结果为.
(1)求出,的值;
(2)请你计算出这道整式乘法题的正确结果.
20.图1是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀剪下全等的四块小长方形,然后按图2拼成一个正方形.
图1 图2
(1)直接写出图2中阴影部分的正方形的边长为
(2)观察图2,请直接写出下列三个代数式(m+n) 2,(m- n) 2,mn之间的等量关系是
(3)根据(2)中的等量关系,解决如下问题:
①若 p+q=9,pq=7,求(p- q) 2的值:
②若(2021- a) 2+( a - 2022) 2=7,求(2021- a) ( a- 2022)的值.
21.若x满足(9-x)(x-4)=4,求的值.
解:设9-x=a,x-4=b,则(9-x)(x-4)=ab=4,a+b=(9-x)+(x-4)=5,
请仿照上面的方法解答下面的问题:
(1)若x满足(x-10)(x-20)=15,求的值.
(2)若x满足(求(x-2023)(x-2024)的值.
(3)如图,已知正方形ABCD的边长为x,E,F分别是AD,DC上的点,且AE=1,CF=3,长方形EMFD的面积是48,分别以MF,DF为边长作正方形MFRN和正方形GFDH,求阴影部分的面积.
答案解析部分
1.【答案】C
【解析】【解答】解:A.与a不是同类项,不能合并,A不符合题意;
B.同底数幂相乘,底数不变,指数相加,,B不符合题意;
C.,C符合题意;
D.同底数幂相除,底数不变,指数相减,,D不符合题意;
故答案为:C.
【分析】根据同底数幂乘除法、积的乘方,同类项相加结合题意对选项逐一分析即可求解。
2.【答案】C
3.【答案】D
【解析】【解答】解:A、,A不符合题意;
B、,B不符合题意;
C、,C不符合题意;
D、,D符合题意;
故答案为:D
【分析】根据完全平方公式、平方差公式结合题意对选项逐一分析即可求解。
4.【答案】B
【解析】【解答】解:A、 (2a+3b)(2a-3b) ,符合平方差公式的结构特点,能用平方差公式计算,故此选项不符合题意;
B、 (-2a+3b)(3b-2a) =(-2a+3b)(-2a+3b) ,不符合平方差公式的结构特点,不能用平方差公式计算,故此选项符合题意;
C、 (-2a+3b)(-2a-3b) ,符合平方差公式的结构特点,能用平方差公式计算,故此选项不符合题意;
D、 (2a-3b)(-2a-3b)=(-3b+2a)(-3b-2a) ,符合平方差公式的结构特点,能用平方差公式计算,故此选项不符合题意.
故答案为:B.
【分析】两个二项式相乘,如果这两个二项式中满足:有一项完全相同,另一项只有符号不同,那么这样的两个二项式相乘,就可以使用平方差公式进行计算,据此逐项判断得出答案.
5.【答案】D
【解析】【解答】解:这个长方形的面积为 (4a2-2a+1)(2a+1)=4a2·(2a+1)-2a(2a+1)+2a+1
= 8a3+1 .
故答案为:D.
【分析】根据长方形的面积=长×宽先列式,再计算即可.
6.【答案】C
7.【答案】D
【解析】【解答】解:最大和最小的两个数是m+8和m-8,
∴n=(m-8)(m+8)=m2-64,
即m2=64+n;
A、当n=377时, 64+377=441=212 ,结果是一个平方数,所以n可能是377,A不符合题意;
B、当n=420时,420+64=484=222,结果是一个平方数,所以n可能是420,B不符合题意;
C、当n=465时,465+64=529=232,结果是一个平方数,所以n可能是465,C不符合题意;
D、当n=512时,512+64=576=242,最小的数是24-8=16,最大的数是24+8=32,不符合实际,D符合题意;
故答案为:D.
【分析】先用含有m的式子表示出最大和最小的两个数,结合题意可得m2=64+n,逐项将n的值代入,判断是否是平方数,注意结合实际,即可判断得出答案.
8.【答案】C
【解析】【解答】解:设正方形①的边长为a,正方形②的边长为b,
∴长方形③的长=a+b,宽=a-b,
∵长方形③的面积为16,
∴(a+b)(a-b)=16,
∴a2-b2=16(1)
∵大长方形的长=2a+b,大长方形的宽=2a-b,
∵大长方形的面积为100,
∴(2a+b)(2a-b)=100,
∴4a2-b2=100(2)
由(2)-(1)×4,得:3b2=36,
∴b2=12,
∴正方形②的面积=b2=12.
故答案为:C.
【分析】设正方形①边长为a,正方形②边长为b,表示出长方形③长=a+b,宽=a-b,由长方形③面积为16,可得(a+b)(a-b)=16,整理得a2-b2=16(1);大长方形长=2a+b,大长方形宽=2a-b,由大长方形面积为100,可得(2a+b)(2a-b)=100,整理得4a2-b2=100(2),再由(2)-(1)×4,得3b2=36,解得b2=12,即可正方形②的面积.
9.【答案】A
【解析】【解答】解:原式=(2-1)(2+1)(22+1)(24+1)…(216+1)
=(22-1)(22+1)(24+1)…(216+1)
=(24-1)(24+1)…(216+1)
=(28-1)…(216+1)
=232-1,
故答案为:A.
【分析】将原式变形为(2-1)(2+1)(22+1)(24+1)…(216+1),然后利用平方差公式计算即可.
10.【答案】C
【解析】【解答】解:由“杨辉三角”的规律可知,
展开式中所有项的系数和为1,
展开式中所有项的系数和为2,
展开式中所有项的系数和为4,
展开式中所有项的系数和为8,
……
展开式中所有项的系数和为,
展开式中所有项的系数和为.
故答案为:C.
【分析】先计算n=0,1,2,3,时,展开式中所有项的系数和,从中得出规律为展开式中所有项的系数和为,再把n=8代入计算即可。
11.【答案】
【解析】【解答】解:原式=,
故答案为:
【分析】根据积的乘方法则,幂的乘方法则,同底数幂的除法法则计算即可.
12.【答案】-1
13.【答案】 或 3 或 1
【解析】【解答】解:由题意得:
①x+1=0,
解得:x=﹣1;
②x﹣2=1,
解得:x=3;
③x﹣2=﹣1,x+1为偶数,
解得:x=1,
故答案为:﹣1或3或1.
【分析】由 知,要分三种情况讨论,即:根据零指数幂可得x+1=0,根据有理数的乘方可得x﹣2=1;x﹣2=﹣1,x+1为偶数,再解方程即可解答.
14.【答案】10
【解析】【解答】解:
∴m-3=0,2-3m+n=0
∴m=3,n=7
∴m+n=10
故答案为:10.
【分析】本题考查整式乘法的计算方法,熟知整式乘法中多项式乘以多项式计算法则是解题关键,根据多项式乘以多项式计算法则展开合并,结合展开式中不含,可得m-3=0,2-3m+n=0解得m,n的值,即可得出答案.
15.【答案】或
【解析】【解答】解:∵a3+3a2+a=a(a2+3a+1)=0,
∴a=0或a2+3a+1=0,
当a=0时,;
当a2+3a+1=0时,,
∴,
∴,
∴,
∴,
综上,的值为0或.
故答案为:0或.
【分析】先将已知方程的左边利用提取公因式法分解因式,进而根据两个因式的乘积等于零,则至少有一个因式为零,从而得出a=0或a2+3a+1=0,从而分两种情况求值;当a=0时易得所求式子的 值为零;当a2+3a+1=0时,等式的两边同时除以a得,再将该式两边同时平方得,进而可求出待求式子的倒数,即可解决此题.
16.【答案】
【解析】【解答】解:设正方形甲、乙、丙的边长为a,
∵正方形甲、乙一组邻边的延长线构成的正方形面积记为S3,且S3=1,大正方形边长为9,
∴2a+1=9,
∴a=4,
设正方形S1,S2的边长分别为x,y,
∴x+y+1=4,即x+y=3①,
又∵S1-S2=2S3,
∴x2-y2=2,即(x+y)(x-y)=2,
∴(x-y)=②,
由①得:x2+2xy+y2=9,
由②得:x2-2xy+y2=,
∴4xy=,
∴xy=,
∴S阴影=(x+1)(y+1)-S3=xy+x+y+1-1,
∴S阴影=+3=.
故答案为:.
【分析】设正方形甲、乙、丙的边长为a,由正方形甲、乙一组邻边延长线构成的正方形面积记为S3,且S3=1,大正方形边长为9,推出2a+1=9,解得a=4,设正方形S1,S2的边长分别为x,y,从而得到x+y+1=4,即x+y=3①,再由S1-S2=2S3,得x2-y2=2,利用平方差公式可求得(x-y)=②,再利用完全平方公式得x2+2xy+y2=9,x2-2xy+y2=,则4xy=,即得xy=,最后根据阴影部分正方形的面积(x+1)(y+1)-S3=xy+x+y+1-1,代入数据计算即可求解.
17.【答案】(1)解:由题意得:;
(2)解:∵,
∴,
∴,
∴,
∴
【解析】【分析】(1)根据新运算,结合同底数幂的乘法即可求出答案.
(2)根据新运算,结合同底数幂的乘法即可求出答案.
18.【答案】解:
,
,
,,
,,
,,
原式.
【解析】【分析】先利用整式的混合运算化简,再利用非负数之和为0的性质求出a、b的值,最后将a、b的值代入计算即可.
19.【答案】(1)解:
由于小马抄错了的符号,得到的结果为:
;
①,
小虎漏抄了第一个多项式中的系数,
得到的结果为,
②,
由①②解得;
故,;
(2)解:由(1)得
;
故这道整式乘法题的正确结果为.
【解析】【分析】(1)根据 小马抄错了的符号,可以进行: ,得出结果为 :,进而可得出 ①;然后再根据小虎漏抄了第一个多项式中的系数,得到的结果为 ,可得出 ②, 联立①②,解方程组,即可得出 ,;
(2)把,代入原式,然后再正确进行计算即可。
20.【答案】(1)m-n
(2)故答案为:(m- n) 2 =(m+n) 2- 4mn;
(3)解:①由(2)可知,
(p - q) 2 = (p +q) 2–4pq
= 81-28
= 53;
②设x=2021-a,y=a-2022,则x+y=-1,x2+y2=7,
∵(x+y) 2= 1
∴x2 + 2xy+y2= 1
2xy= -6
xy= -3
∴(2021- a)(a - 2022)的值为-3.
【解析】【解答】解:(1)图2中的阴影部分的正方形的边长等于.
故答案为:,
(2)由题意得:小正方形面积等于大正方形的面积减去4个长方形的面积,即,阴影部分正方形的面积为,
所以,
故答案为:(m- n) 2 =(m+n) 2- 4mn;
【分析】(1)观察得到阴影部分的正方形的边长等与长为m,宽为n的长方形的长宽之差;
(2)小正方形面积等于大正方形的面积减去4个长方形的面积,即,阴影部分正方形的面积为,根据等面积法即可求解.
(3)①根据(2)的等量关系进行计算即可求解;
②设x=2021-a,y=a-2022,则x+y=-1,x2+y2=7,可推出xy= -3,即可得解.
21.【答案】(1)解:设x-10=a,x-20=b,
则 (x-10)(x-20)=ab=15, (x-10)-(x-20)=a-b=10,
∴(x-10)2+(x-20)2=a2+b2=(a-b)2+2ab=102+2×15=130.
(2)解:设x-2023=a,x-2024=b,
则 (x-2023)2+(x-2024)2=a2+b2=33, (x-2023)-(x-2024)=a-b=1,
∴(a-b)2=12,
∴a2-2ab+b2=1,
∴33-2ab=1,解得:ab=16,
故(x-2023)(x-2024)=ab=16.
(3)解:∵正方形的边长为x,AE=1,CF=3,
∴FM=DE=x-1,DF=x-3,
∴(x-1)(x-3)=48,
∴(x-1)-(x-3)=2,
∴阴影部分的面积=FM2-DF2=(x-1)2-(x-3)2,
设x-1=a,x-3=b,则(x-1)(x-3)=ab=48,a-b=(x-1)-(x-3)=2,
∴(a+b)2=(a-b)2+4ab=4+192=196,
∵a>0,b>0,
∴a+b>0,
∴a+b=14,
∴(x-1)2-(x-3)2
=a2-b2
=(a+b)(a-b)
=14×2=28.
即阴影部分的面积为28.
【解析】【分析】(1)设x-2023=a,x-2024=b,由已知条件得ab=1,a-b=10,根据a2+b2=(a-b)2+2ab即可求解;
(2)设x-2023=a,x-2024=b,结合已知可得a2+b2=33,a-b=2,将a-b=2两边分别平方,然后整体代换即可求解;
(3)观察图形,根据线段的构成将FM=DE,DF用含x的代数式表示出来,根据阴影部分的面积=FM2-DF2=(x-1)2-(x-3)2,根据(2)的方法计算即可求解.
1 / 1
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
