浙教七年级下册第1章 平行线 小结 教学设计(表格式)
文档属性
| 名称 | 浙教七年级下册第1章 平行线 小结 教学设计(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 271.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-05 07:31:20 | ||
图片预览

文档简介
教学设计
课程基本信息
学科 初中数学 年级 七年级 学期 春季
课题 第一章平行线复习
教学目标
1.使学生认识平面内两条直线的位置关系,在研究平行线时,能通过有关的角来判断直线平行和反映平行线的性质,理解平移的性质,能利用平移设计图案。 2.使学生能够熟练掌握平行线的判定及性质,并学会简单推理过程,培养学生的归纳能力,分析问题能力和推理能力。
教学内容
教学重点: 1.进一步体会三线八角模型,熟练掌握平行线的性质与判定。 2.初步感受添加辅助线解决几何问题的思路。 教学难点: 1.平行的性质和判定的综合应用,遇到复杂问题的分析过程和书写推理过程。
2.运用一题多解,多种添辅助线的方法,通过综合应用进一步加深对该知识的理解。
教学过程
一、知识梳理 经历对本章所学知识回顾与思考的过程,将本章内容条理化,系统化,梳理本章的知识结构,并画出本章的知识结构系统思维导图。
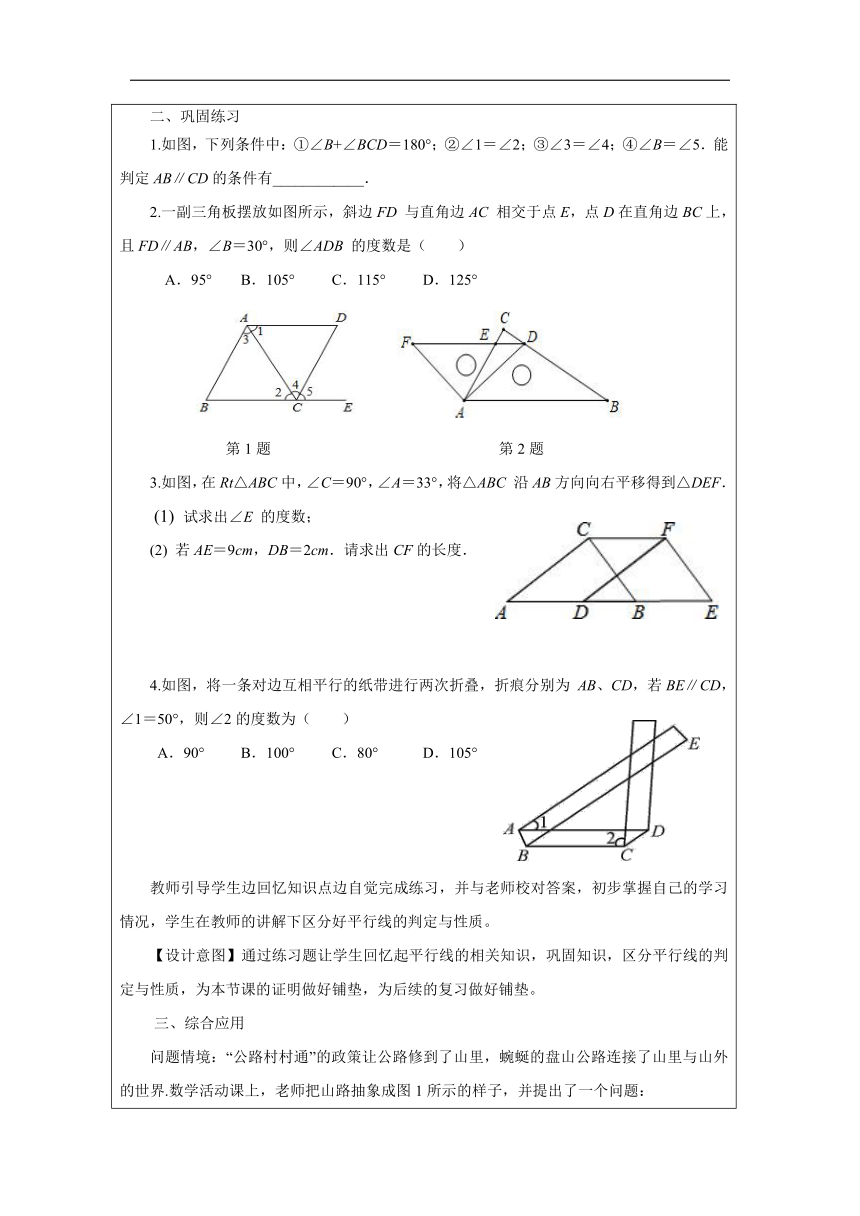
二、巩固练习 1.如图,下列条件中:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5.能判定AB∥CD的条件有____________. 2.一副三角板摆放如图所示,斜边FD 与直角边AC 相交于点E,点D在直角边BC上,且FD∥AB,∠B=30°,则∠ADB 的度数是( ) A.95° B.105° C.115° D.125° 第1题 第2题 3.如图,在Rt△ABC中,∠C=90°,∠A=33°,将△ABC 沿AB方向向右平移得到△DEF. (1) 试求出∠E 的度数; (2) 若AE=9cm,DB=2cm.请求出CF的长度. 4.如图,将一条对边互相平行的纸带进行两次折叠,折痕分别为 AB、CD,若BE∥CD, ∠1=50°,则∠2的度数为( ) A.90° B.100° C.80° D.105° 教师引导学生边回忆知识点边自觉完成练习,并与老师校对答案,初步掌握自己的学习情况,学生在教师的讲解下区分好平行线的判定与性质。 【设计意图】通过练习题让学生回忆起平行线的相关知识,巩固知识,区分平行线的判定与性质,为本节课的证明做好铺垫,为后续的复习做好铺垫。 三、综合应用 问题情境:“公路村村通”的政策让公路修到了山里,蜿蜒的盘山公路连接了山里与山外的世界.数学活动课上,老师把山路抽象成图1所示的样子,并提出了一个问题: AB//CD,∠B=125°,∠C=25°,求 ∠BPC的度数。 请问同学们本题还有其他的解题方法吗? 聪明的小明在图1的基础上,将图1改变为图2,其中 AB//CD,∠B=125°,∠PQC=65°,∠C=145° ,求∠BPQ的度数。 图1 图2 解:如图1,过点P作PQ//AB, ∵AB//CD, ∴PQ//CD(平行于同一条直线的两条直线互相平行). ∵AB//PQ, ∴∠B+∠BPQ=180°(两条直线平行,同旁内角互补). ∵∠B=125°, ∴∠BPQ=55°. ∵PQ//CD, ∠C=25°,∴∠C=∠CPD=25°. ∴∠BPC=∠BPQ+∠CPD=55°+25°=80°. 解:延长BP交CD于点E, ∵AB//CD, ∴∠B+∠BEC=180°. ∵ ∠B=125°, ∴∠BEC=55°. ∵∠C=25°, ∴∠CPE=180°-55°-25°=100°. ∴∠BPC+∠CPE=180°,∴∠BPC=180°-∠CPE=180°-100°=80°. 解题小结: 在解决平行线间的拐角问题时,当无法直接得到角的关系时,通常借助辅助线来帮助解答,如何作辅助线需根据已知条件确定,辅助线的添加既可以产生新的条件,又能将题目中原有的条件联系在一起。 常见辅助线的作法:(1)过“拐点”作平行线;(2)过“拐点”加截线(连接两点或延长线段)。 (3)解:过点P作PN//AB,过点Q作QM//AB, ∵AB//CD, ∴AB//PN//QM//CD. ∴∠B+∠1=180°,∠2=∠3,∠4+∠C=180°. ∵ ∠B=125°, ∠C=145°, ∴∠1=180°-∠B=180°-125°=55°.∠4=180°-∠C=180°-145°=35°. ∵ ∠PQC=65°,∴∠3=∠PQC-∠4=65°-35°=30°. ∴∠2=∠3=30°. ∴∠BPQ=∠1+∠2 =55°+30°=85°. 【设计意图】本题运用一题多解,多种添辅助线的方法让学生在熟知并区分了平行线的判定与性质后,通过综合应用进一步加深对该知识的理解。本题通过作辅助线构造基本图形,把问题转化为平行线的性质和判定的问题,从而建立起角之间的关系。 教师强调拐点问题的重要性,并说明辅助线的做法,展示题目解答过程.学生能注意到教师强调的内容,对拐点问题有了初步的了解。 四、配套练习,助力提升 1.如图,在三角形 ABC中,点D, E,F分别在 AB,AC, BC上,DE//BC , ∠C=∠EDF,则下列结论错误的是( ) A. ∠ADE=∠B B. DF//AC C. ∠BFD=∠AED D.∠B+∠CED=180 2.有一条长方形纸带,按如图所示沿AB折叠时,当∠1=30°,时求纸带重叠部分中∠CAB的度数为_________. 第1题 第2题 3.已知 AM∥CN,点B在直线AM、CN之间,∠ABC=88°. (1)如图1,请直接写出∠A和∠C之间的数量关系:____________. (2)如图2,∠A和∠C满足怎样的数量关系?请说明理由. (3)如图3,AE平分∠MAB,CH平分∠NCB,AE与CH交于点G,求∠AGH的度数. 五、课堂小结 1.解决平行线问题的常用方法是什么? 2.添加辅助线的常用方法是什么?具体如何操作? 六、布置作业 作业编制:你能将综合应用题中“平行线间的拐角问题”进行修改,编制出一道过拐点添辅助线的方法解决的实际问题吗?
课程基本信息
学科 初中数学 年级 七年级 学期 春季
课题 第一章平行线复习
教学目标
1.使学生认识平面内两条直线的位置关系,在研究平行线时,能通过有关的角来判断直线平行和反映平行线的性质,理解平移的性质,能利用平移设计图案。 2.使学生能够熟练掌握平行线的判定及性质,并学会简单推理过程,培养学生的归纳能力,分析问题能力和推理能力。
教学内容
教学重点: 1.进一步体会三线八角模型,熟练掌握平行线的性质与判定。 2.初步感受添加辅助线解决几何问题的思路。 教学难点: 1.平行的性质和判定的综合应用,遇到复杂问题的分析过程和书写推理过程。
2.运用一题多解,多种添辅助线的方法,通过综合应用进一步加深对该知识的理解。
教学过程
一、知识梳理 经历对本章所学知识回顾与思考的过程,将本章内容条理化,系统化,梳理本章的知识结构,并画出本章的知识结构系统思维导图。
二、巩固练习 1.如图,下列条件中:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5.能判定AB∥CD的条件有____________. 2.一副三角板摆放如图所示,斜边FD 与直角边AC 相交于点E,点D在直角边BC上,且FD∥AB,∠B=30°,则∠ADB 的度数是( ) A.95° B.105° C.115° D.125° 第1题 第2题 3.如图,在Rt△ABC中,∠C=90°,∠A=33°,将△ABC 沿AB方向向右平移得到△DEF. (1) 试求出∠E 的度数; (2) 若AE=9cm,DB=2cm.请求出CF的长度. 4.如图,将一条对边互相平行的纸带进行两次折叠,折痕分别为 AB、CD,若BE∥CD, ∠1=50°,则∠2的度数为( ) A.90° B.100° C.80° D.105° 教师引导学生边回忆知识点边自觉完成练习,并与老师校对答案,初步掌握自己的学习情况,学生在教师的讲解下区分好平行线的判定与性质。 【设计意图】通过练习题让学生回忆起平行线的相关知识,巩固知识,区分平行线的判定与性质,为本节课的证明做好铺垫,为后续的复习做好铺垫。 三、综合应用 问题情境:“公路村村通”的政策让公路修到了山里,蜿蜒的盘山公路连接了山里与山外的世界.数学活动课上,老师把山路抽象成图1所示的样子,并提出了一个问题: AB//CD,∠B=125°,∠C=25°,求 ∠BPC的度数。 请问同学们本题还有其他的解题方法吗? 聪明的小明在图1的基础上,将图1改变为图2,其中 AB//CD,∠B=125°,∠PQC=65°,∠C=145° ,求∠BPQ的度数。 图1 图2 解:如图1,过点P作PQ//AB, ∵AB//CD, ∴PQ//CD(平行于同一条直线的两条直线互相平行). ∵AB//PQ, ∴∠B+∠BPQ=180°(两条直线平行,同旁内角互补). ∵∠B=125°, ∴∠BPQ=55°. ∵PQ//CD, ∠C=25°,∴∠C=∠CPD=25°. ∴∠BPC=∠BPQ+∠CPD=55°+25°=80°. 解:延长BP交CD于点E, ∵AB//CD, ∴∠B+∠BEC=180°. ∵ ∠B=125°, ∴∠BEC=55°. ∵∠C=25°, ∴∠CPE=180°-55°-25°=100°. ∴∠BPC+∠CPE=180°,∴∠BPC=180°-∠CPE=180°-100°=80°. 解题小结: 在解决平行线间的拐角问题时,当无法直接得到角的关系时,通常借助辅助线来帮助解答,如何作辅助线需根据已知条件确定,辅助线的添加既可以产生新的条件,又能将题目中原有的条件联系在一起。 常见辅助线的作法:(1)过“拐点”作平行线;(2)过“拐点”加截线(连接两点或延长线段)。 (3)解:过点P作PN//AB,过点Q作QM//AB, ∵AB//CD, ∴AB//PN//QM//CD. ∴∠B+∠1=180°,∠2=∠3,∠4+∠C=180°. ∵ ∠B=125°, ∠C=145°, ∴∠1=180°-∠B=180°-125°=55°.∠4=180°-∠C=180°-145°=35°. ∵ ∠PQC=65°,∴∠3=∠PQC-∠4=65°-35°=30°. ∴∠2=∠3=30°. ∴∠BPQ=∠1+∠2 =55°+30°=85°. 【设计意图】本题运用一题多解,多种添辅助线的方法让学生在熟知并区分了平行线的判定与性质后,通过综合应用进一步加深对该知识的理解。本题通过作辅助线构造基本图形,把问题转化为平行线的性质和判定的问题,从而建立起角之间的关系。 教师强调拐点问题的重要性,并说明辅助线的做法,展示题目解答过程.学生能注意到教师强调的内容,对拐点问题有了初步的了解。 四、配套练习,助力提升 1.如图,在三角形 ABC中,点D, E,F分别在 AB,AC, BC上,DE//BC , ∠C=∠EDF,则下列结论错误的是( ) A. ∠ADE=∠B B. DF//AC C. ∠BFD=∠AED D.∠B+∠CED=180 2.有一条长方形纸带,按如图所示沿AB折叠时,当∠1=30°,时求纸带重叠部分中∠CAB的度数为_________. 第1题 第2题 3.已知 AM∥CN,点B在直线AM、CN之间,∠ABC=88°. (1)如图1,请直接写出∠A和∠C之间的数量关系:____________. (2)如图2,∠A和∠C满足怎样的数量关系?请说明理由. (3)如图3,AE平分∠MAB,CH平分∠NCB,AE与CH交于点G,求∠AGH的度数. 五、课堂小结 1.解决平行线问题的常用方法是什么? 2.添加辅助线的常用方法是什么?具体如何操作? 六、布置作业 作业编制:你能将综合应用题中“平行线间的拐角问题”进行修改,编制出一道过拐点添辅助线的方法解决的实际问题吗?
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
