浙教版七年级下册第2章 二元一次方程组 复习小结 教学设计(表格式)
文档属性
| 名称 | 浙教版七年级下册第2章 二元一次方程组 复习小结 教学设计(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 161.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-05 07:32:25 | ||
图片预览


文档简介
教学设计
课程基本信息
学科 数学 年级 七年级 学期 (秋季)
课题 二元一次方程组复习
教学目标
1.通过本节课的学习使同学进一步理解并掌握二元一次方程(组)的相关概念,能够选择合适的方法解二元一次方程组. 2.通过本节课对二元一次方程组的总结和复习,使学生能够利用二元一次方程(组)的知识, 解决一些综合问题. 3.通过对一些题目的探索和运用,培养同学的获取信息、分析问题的方法,促进解题能力的提升. 4.通过对一元二次方程组单元的复习,培养学生整体认识能力,建立知识方法的框架结构.
教学内容
教学重点: 熟练选择消元的方法解二元一次方程组.
教学难点: 学习分析综合问题的方法.
教学过程
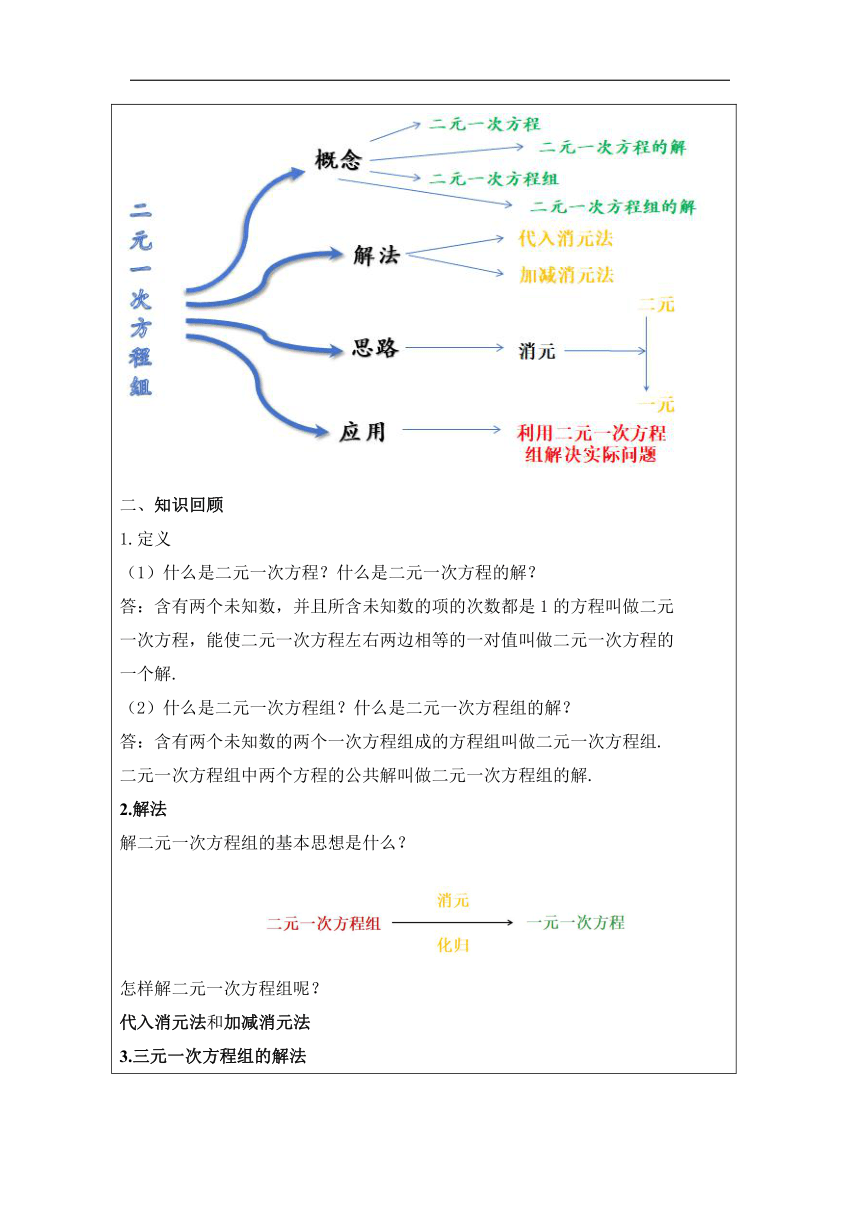
一、知识脉络 二、知识回顾 1.定义 (1)什么是二元一次方程?什么是二元一次方程的解? 答:含有两个未知数,并且所含未知数的项的次数都是1的方程叫做二元 一次方程,能使二元一次方程左右两边相等的一对值叫做二元一次方程的 一个解. (2)什么是二元一次方程组?什么是二元一次方程组的解? 答:含有两个未知数的两个一次方程组成的方程组叫做二元一次方程组. 二元一次方程组中两个方程的公共解叫做二元一次方程组的解. 2.解法 解二元一次方程组的基本思想是什么? 怎样解二元一次方程组呢? 代入消元法和加减消元法 3.三元一次方程组的解法 4.二元一次方程组的应用 三、典例精解 例1 解方程组: (1) (2) 解:(1)把①代入②,得x+x+1=5 解得x=2 把x=2代入①,得y=3 所以方程组的解为 (2)①+②,得4x=8 解得x=2 把x=2代入①,得2+2y=9 解得y= 所以方程组的解为 点评:方程组(1)中有一个方程是用一个字母表示另一个字母形式,可用代入法解;方程组(2)中有一个字母的系数互为相反数,可用加减法解. 例2 解方程组: (1) (2) 解:由②,得3x+2y=15③, 由①,得y=5-4x, 把y=5-4x代入③, 得3x+2(5-4x)=15 解得x=-1, 把x=-1代入y=5-4x,得y=9 所以方程组的解为 (2)由①,得2x-3y=9 ③ , 由②,得2x-y=3④, ③-④ ,得-2y=6,即y=-3, 把y=-3代入④ ,得2x-(-3)=3, 解得x=0, 所以方程组的解为 点评:对于含有分母或括号的方程组,可先分别化简方程组中的各个方程,再选择适当的方法求解. 例3 解方程组: 解:由②-①,得3(x-y)=6 ,解得x-y=2③, 把x-y=2代入①,得x+y=④, 得新方程组解得: 所以方程组的解为 点评:运用整体思想求解. 例4 解方程组: 解:由①-②,得-2b=4,解得b=-2 , 把b=-2分别代入① ,③得 解得a=1,c=-3 所以方程组的解为 点评:三元一次方程组化为二元一次方程组,二元一次方程组再化为一元一次方程求解. 例5 端午临仲夏,时清日复长.“临近端午节,一网红门店接 到一份粽子订单,立即决定由甲、乙两组加工完成.已知甲、 乙两组加工一天共生产350袋粽子,甲组加工2天比乙组加工1 天多生产250袋粽子.
(1)求甲、乙两组平均每天各能加工多少袋粽子?
(2)已知这份粽子订单为1700袋,若甲、乙两组共用10天加 工完成,则甲组需要加工多少天? 解:(1)设甲组平均每天能加 工x袋粽子,乙组平均每天能加 工y袋粽子, 由题意得: 解得:. 答:甲组平均每天能加工200袋粽子,乙组平均每天能加工150袋粽子. (2)设甲组需要加工m天,则乙组加工(10-m)天, 由题意得:200m+150(10-m)=1700, 解得:m=4, 答:甲组需要加工4天. 点评:利用二元一次方程组解决实际应用,关键是找准等量关系. 三、小试牛刀 1.下列方程中是二元一次方程的是( ) A.x=2y B.x+2y=z C.xy+1=0 D. 2.下列方程组属于二元一次方程组的是( ) A. B. C. D. 3.若方程xm+2+4y3n-2=4是关于x,y的二元一次方程,则(m+n)2023= . 4.若是方程ax+by=3的解,则2a+4b+5= . 5.若方程组的解为,则a+b的值为 .
6.解方程组: (1) (2) (3) (4) 参考答案 1.A 2.D 3.-1 4.11 5.1 6. (1)(2)(3)(4)
课程基本信息
学科 数学 年级 七年级 学期 (秋季)
课题 二元一次方程组复习
教学目标
1.通过本节课的学习使同学进一步理解并掌握二元一次方程(组)的相关概念,能够选择合适的方法解二元一次方程组. 2.通过本节课对二元一次方程组的总结和复习,使学生能够利用二元一次方程(组)的知识, 解决一些综合问题. 3.通过对一些题目的探索和运用,培养同学的获取信息、分析问题的方法,促进解题能力的提升. 4.通过对一元二次方程组单元的复习,培养学生整体认识能力,建立知识方法的框架结构.
教学内容
教学重点: 熟练选择消元的方法解二元一次方程组.
教学难点: 学习分析综合问题的方法.
教学过程
一、知识脉络 二、知识回顾 1.定义 (1)什么是二元一次方程?什么是二元一次方程的解? 答:含有两个未知数,并且所含未知数的项的次数都是1的方程叫做二元 一次方程,能使二元一次方程左右两边相等的一对值叫做二元一次方程的 一个解. (2)什么是二元一次方程组?什么是二元一次方程组的解? 答:含有两个未知数的两个一次方程组成的方程组叫做二元一次方程组. 二元一次方程组中两个方程的公共解叫做二元一次方程组的解. 2.解法 解二元一次方程组的基本思想是什么? 怎样解二元一次方程组呢? 代入消元法和加减消元法 3.三元一次方程组的解法 4.二元一次方程组的应用 三、典例精解 例1 解方程组: (1) (2) 解:(1)把①代入②,得x+x+1=5 解得x=2 把x=2代入①,得y=3 所以方程组的解为 (2)①+②,得4x=8 解得x=2 把x=2代入①,得2+2y=9 解得y= 所以方程组的解为 点评:方程组(1)中有一个方程是用一个字母表示另一个字母形式,可用代入法解;方程组(2)中有一个字母的系数互为相反数,可用加减法解. 例2 解方程组: (1) (2) 解:由②,得3x+2y=15③, 由①,得y=5-4x, 把y=5-4x代入③, 得3x+2(5-4x)=15 解得x=-1, 把x=-1代入y=5-4x,得y=9 所以方程组的解为 (2)由①,得2x-3y=9 ③ , 由②,得2x-y=3④, ③-④ ,得-2y=6,即y=-3, 把y=-3代入④ ,得2x-(-3)=3, 解得x=0, 所以方程组的解为 点评:对于含有分母或括号的方程组,可先分别化简方程组中的各个方程,再选择适当的方法求解. 例3 解方程组: 解:由②-①,得3(x-y)=6 ,解得x-y=2③, 把x-y=2代入①,得x+y=④, 得新方程组解得: 所以方程组的解为 点评:运用整体思想求解. 例4 解方程组: 解:由①-②,得-2b=4,解得b=-2 , 把b=-2分别代入① ,③得 解得a=1,c=-3 所以方程组的解为 点评:三元一次方程组化为二元一次方程组,二元一次方程组再化为一元一次方程求解. 例5 端午临仲夏,时清日复长.“临近端午节,一网红门店接 到一份粽子订单,立即决定由甲、乙两组加工完成.已知甲、 乙两组加工一天共生产350袋粽子,甲组加工2天比乙组加工1 天多生产250袋粽子.
(1)求甲、乙两组平均每天各能加工多少袋粽子?
(2)已知这份粽子订单为1700袋,若甲、乙两组共用10天加 工完成,则甲组需要加工多少天? 解:(1)设甲组平均每天能加 工x袋粽子,乙组平均每天能加 工y袋粽子, 由题意得: 解得:. 答:甲组平均每天能加工200袋粽子,乙组平均每天能加工150袋粽子. (2)设甲组需要加工m天,则乙组加工(10-m)天, 由题意得:200m+150(10-m)=1700, 解得:m=4, 答:甲组需要加工4天. 点评:利用二元一次方程组解决实际应用,关键是找准等量关系. 三、小试牛刀 1.下列方程中是二元一次方程的是( ) A.x=2y B.x+2y=z C.xy+1=0 D. 2.下列方程组属于二元一次方程组的是( ) A. B. C. D. 3.若方程xm+2+4y3n-2=4是关于x,y的二元一次方程,则(m+n)2023= . 4.若是方程ax+by=3的解,则2a+4b+5= . 5.若方程组的解为,则a+b的值为 .
6.解方程组: (1) (2) (3) (4) 参考答案 1.A 2.D 3.-1 4.11 5.1 6. (1)(2)(3)(4)
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
