浙教版七年级下册第三章 整式的乘除单元检测 含解析
文档属性
| 名称 | 浙教版七年级下册第三章 整式的乘除单元检测 含解析 |  | |
| 格式 | docx | ||
| 文件大小 | 145.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-14 20:59:50 | ||
图片预览




文档简介
浙教版七年级下册第三章整式的乘除单元检测
一、选择题(每题3分,共30分)
1.即空气中的细颗粒物,它的直径不超过0.0025毫米,以下用科学记数法表示数字0.0025正确的是( )
A. B. C. D.
2.下列运算正确的是( )
A. B. C. D.
3.下列整式中,属于完全平方式的是( )
A. B. C. D.
4.若,.则等于( )
A. B. C. D.0
5.如果m2+m=5,那么代数式 的值为( )
A.14 B.9 C.1 D.6
6.计算(-6x-5y)(5y-6x)的结果是( ).
A. B.
C. D.
7.若,则,的值分别是( )
A., B.,
C., D.,
8.如图①,在边长为a的正方形中剪去一个边长为b(bA.a2+b2=(a+b)(a-b) B.(a-b)2=a2-2ab+b2
C.(a+b)2=a2+2ab+b2 D.a2-b2=(a+b)(a-b)
9.若A=(2+1)(22+1)(24+1)(28+1)+1,则A的末位数字是( )
A.2 B.4 C.6 D.8
10.关于的多项式:,其中为正整数,若各项系数各不相同且均不为0,我们称这样的多项式为“亲缘多项式”.
①是“亲缘多项式”.
②若多项式和均为“亲缘多项式”,则也是“亲缘多项式”.
③多项式是“亲缘多项式”且.
④关于的多项式,若,,为正整数,则为“亲缘多项式”.
以上说法中正确的个数是( )
A.1 B.2 C.3 D.4
二、填空题(每题4分,共24分)
11.若 ,则 。
12.若 的乘积中不含 的一次项,则常数 .
13.若x2﹣mx+16是一个完全平方式,则m= .
14.如图,边长为6的正方形ABCD中放置两个长和宽分别为a,b的长方形,若长方形的周长为 16,面积为 15.75,则图中阴影部分的面积S = .
15.已知甲、乙两个长方形,它们的边长如图所示(为正整数),甲、乙的面积分别为,.
(1)与的大小关系为: (填“>”“=”或“<”);
(2)若满足的整数有且只有2个,则的值是 .
16.如果一个三位自然数的各数位上的数字互不相等且均不为0,满足,那么称这个三位数为“中庸数”.将“中庸数”的百位、个位数字交换位置,得到另一个“中庸数”,记.例如:.,.计算 ;若“中庸数”满足,其中为自然数1,2,3……,则该“中庸数”是 .
三、解答题(共8题,共66分)
17.已知.
(1)化简A;
(2)若,求A的值.
18.设 n 为正整数,且求 '的值。
19.小马和小睿两人共同计算--道整式乘法题:(3x+a)(2x+b),由于小马抄错了a的符号,得到的结果为6x2-17x+12;由于小睿漏抄了第二个多项式中x的系数,得到的结果为3x2-5x-12.
(1)求出a,b的值.
(2)请你计算出这道整式乘法题的正确结果.
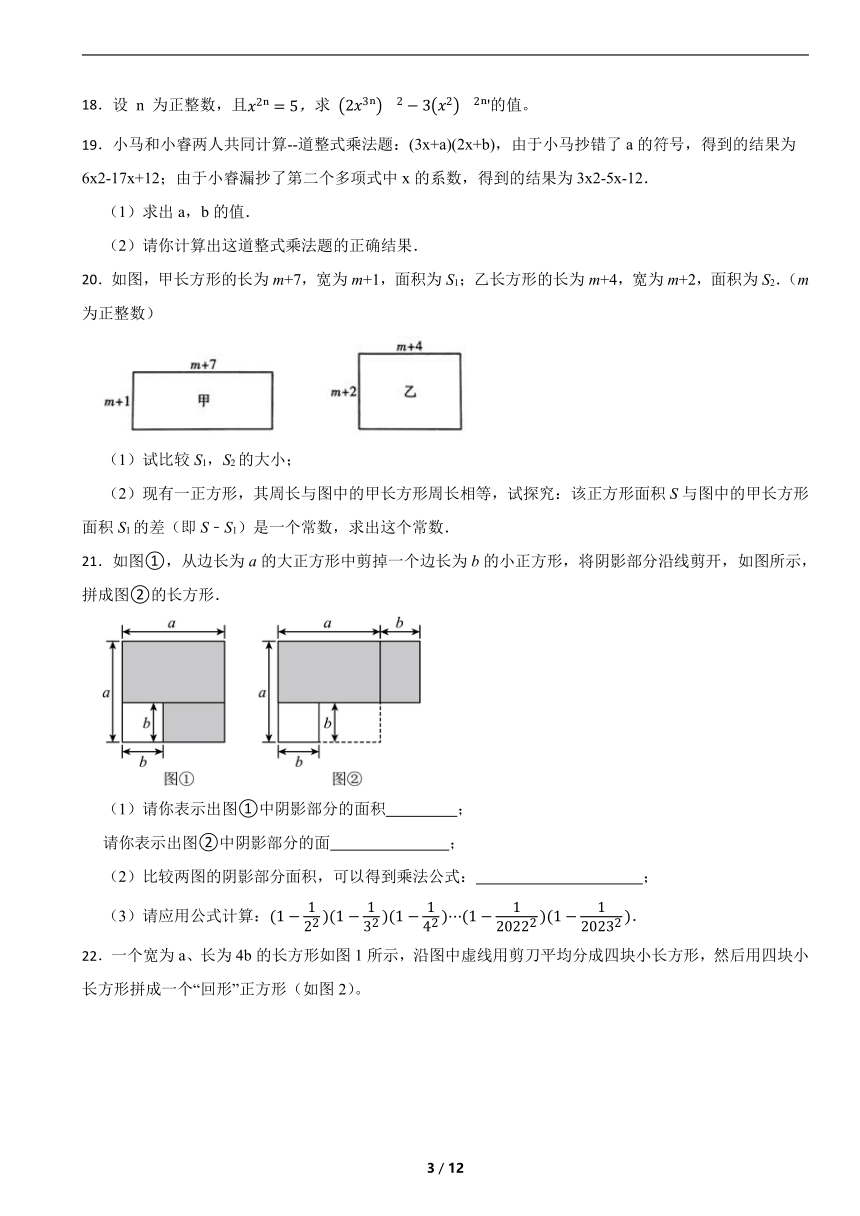
20.如图,甲长方形的长为m+7,宽为m+1,面积为S1;乙长方形的长为m+4,宽为m+2,面积为S2.(m为正整数)
(1)试比较S1,S2的大小;
(2)现有一正方形,其周长与图中的甲长方形周长相等,试探究:该正方形面积S与图中的甲长方形面积S1的差(即S﹣S1)是一个常数,求出这个常数.
21.如图①,从边长为a的大正方形中剪掉一个边长为b的小正方形,将阴影部分沿线剪开,如图所示,拼成图②的长方形.
(1)请你表示出图①中阴影部分的面积 ;
请你表示出图②中阴影部分的面 ;
(2)比较两图的阴影部分面积,可以得到乘法公式: ;
(3)请应用公式计算:.
22.一个宽为a、长为4b的长方形如图1所示,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成一个“回形”正方形(如图2)。
(1)观察图2,请你用等式表示(a+b)2,(a-b)2,
ab之间的数量关系: 。
(2)根据(1)中的结论,如果x+y=5,xy=,求代数式(x-y)2的值。
(3)如果(2019-m)2+(m-2020)2=7。
求(2019-m)(m-2020)的值。
答案解析部分
1.【答案】D
【解析】【解答】解:0.0025用科学记数法表示为,故D正确.
故答案为:D.
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正整数;当原数的绝对值<1时,n是负整数,据此判断即可.
2.【答案】B
【解析】【解答】A. ,不符合题意;
B. ,符合题意;
C. ,不符合题意;
D. ,不符合题意
故答案为:B
【分析】根据同底幂乘、除法,乘方运算以及加减运算规则分别求解判断.
3.【答案】D
4.【答案】C
【解析】【解答】解: ∵,.
∴=a3m÷a2n=(am)3÷(an)2=33÷22=.
故答案为:C.
【分析】利用同底数幂的除法、幂的乘方将原式化为(am)3÷(an)2,再代入计算即可.
5.【答案】A
【解析】【解答】
∵m2+m=5,
∴原式 ,
故答案为:A.
【分析】先化简代数式,再将m2+m=5代入求解即可。
6.【答案】A
【解析】【解答】解: (-6x-5y)(5y-6x)
= -(5y+6x)(5y-6x)
=-[(5y)2-(6x)2]
=-(25y2-36x2)
=36x2-25y2.
故答案为:A.
【分析】从第一个因式中提出一个负号并将括号内的项交换位置变形成平方差公式的标准形式,进而利用平方差公式计算,最后去括号即可得出答案.
7.【答案】A
【解析】【解答】∵,,
∴,,
故答案为:A.
【分析】先利用多项式乘多项式的计算方法展开,再利用待定系数法求出a、b的值即可。
8.【答案】D
【解析】【解答】解:∵左图中阴影部分的面积是a2-b2,右图中梯形的面积是 (2a+2b)(a-b)=(a+b)(a-b),
∴a2-b2=(a+b)(a-b).
故答案为:D.
【分析】根据左图中阴影部分的面积是a2-b2,右图中梯形的面积是 (2a+2b)(a-b)=(a+b)(a-b),利用面积相等即可解答.
9.【答案】C
【解析】【解答】解:∵A=(2+1)(22+1)(24+1)(28+1)+1,
∴A=(2-1)(2+1)(22+1)(24+1)(28+1)+1,
=(22-1)(22+1)(24+1)(28+1)+1,
=(24-1)(24+1)(28+1)+1,
=(28-1)(28+1)+1,
=216-1+1,
=216.
∵21=2,22=4,23=8,24=16,25=32,
∴末位数字以4为周期,
∴16=4×4,
∴216的末位数字是6,
∴原式末位数字是6.
故答案为:C.
【分析】将原式转化成A=(2-1)(2+1)(22+1)(24+1)(28+1)+1,利用平方差公式计算即可得A=216,再以2的幂的末位数字以4为周期,由16=4×4得原式末位数字.
10.【答案】B
【解析】【解答】解:①=4x2-4x+1,且各项系数各不相同且均不为0,
∴是" 亲缘多项式 ",故①正确;
② 原式,无法确定各项系数各不相同且均不为0 ,
∴原式不是" 亲缘多项式 ",故②不正确;
③∵是"亲缘多项式",
∴b4=16,b2=24,b0=1
∴b4+b2+b0=41,故③正确;
④当a=1,b=-1时,n=4时,
(x-1)4=x4-4x3+6x2-4x+1,其中三次项系数与一次项系数相同,
∴(x-1)4不是" 亲缘多项式 ",故④不正确;
∴ 正确的个数是2个;
故答案为:B.
【分析】①利用完全平方公式将展开,根据" 亲缘多项式 "的定义判断即可;
②先合并同类项,再根据" 亲缘多项式 "的定义判断即可;
③将(2x-1)4展开,根据" 亲缘多项式 "的定义判断即可;
④用特殊值法进行判断即可.
11.【答案】3或1.
【解析】【解答】解 :① : 得:t-3=0,解得t=3,
② ;t-2=1,t=3;
③t-2=-1,t=1;
故答案为:3或1.
【分析】此题分三类讨论,①根据零指数的意义得出t-3=0,解得t=3,②根据1的任何次幂=1得出t-2=1,t=3;③根据-1的偶次幂等于1得出t-2=-1,t=1;综上所述从而得出答案。
12.【答案】6
【解析】【解答】∵ 的乘积中不含 的一次项,
∴ = 中
∴
故答案为:6.
【分析】直接利用多项式乘法去括号,进而得出一次项系数为0,求解即可.
13.【答案】
【解析】【解答】解:∵ x2﹣mx+16是一个完全平方式
∴x2﹣mx+16=(x±4)2
∴x2﹣mx+16=x2±8x+16
∴m=±8
故答案为:±8
【分析】根据完全平方公式的结构特点,可知x2﹣mx+16=(x±4)2,将等式右边的括号展开,就可得到m的值。注意:完全平方公式有两个。
14.【答案】12.5
【解析】【解答】解:由题可得:
即
故答案为:12.5.
【分析】根据长方形的周长为16,面积为15.75,得到结合图形用含a,b的式子表示S1,S2,S3,利用完全平方公式计算出的值,从而求解.
15.【答案】(1)
(2)1011
【解析】【解答】解:(1)根据图示知:S1=(m+4)(m+2)=m2+6m+8,S2=(m+7)(m+1)=m2+8m+7,
∴S1-S2=(m2+6m+8)-(m2+8m+7)=-2m+1,
∵m为正整数,
∴m≥1,
∴-2m≤-2,
∴-2m+1≤-2+1,
∴-2m+1<0,
∴S1-S2<0,
∴S1<S2;
故答案为:<;
(2)由(1)知:丨S2-S1丨=丨-2m+1丨=2m-1,
∵丨S2-S1丨<n≤2023的整数n只有两个,
∴整数n为:2022,2023,
∴丨S2-S1丨=2021,
∴2m-1=2021,
∴m=1011,
故答案为:1011.
【分析】(1)首先根据长方形的面积计算公式求得S1=m2+6m+8和S2=m2+8m+7,然后计算S1-S2=-2m+1,根据m为正整数,可判断S1-S2<0,进而得出S1<S2的结论;
(2)由(1)知,-2m+1<0,可得丨S2-S1丨=2m-1,根据S2-S1丨<n≤2023的整数n只有两个,可得整数n为:2022,2023,故而得出丨S2-S1丨=2021,即2m-1=2021,解方程,即可求出m的值。
16.【答案】2;121或484或583
【解析】【解答】解:由题意得:,
因为,,
,
均为完全平方数,
即,为完全平方数,且为偶数,可能为4、16、36、64、100等,
则,可能为0、2、8、18、50等,
因为,,
所以,只可能为0,2,8,
可得当时,或;当时,,
所以或或,,
可得或484或583.
故答案为:2;121或484或583
【分析】先根据题意结合整式的混合运算得到,均为完全平方数,进而结合题意即可得到,可能为0、2、8、18、50等,从而即可求出或或,,再计算m即可求解。
17.【答案】(1)解:;
(2)解:∵,
∴,
∴
.
18.【答案】解:∵
∴
【解析】【分析】根据积的乘方进行化简,并整体代入计算即可.
19.【答案】(1)解:∵小马抄错了a的符号,得到的结果为6x2-17x+12,
∴
即;
∵小睿漏抄了第二个多项式中x的系数,得到的结果为3x2-5x-12,
∴(3x+a)(x+b)=3x2-5x-12,
即a+3b=-5,
故可得,
解得.
(2)解:∵a=4,b=-3,
∴.
【解析】【分析】(1)分别根据多项式与多项式相乘的法则:多项式与多项式相乘,先用一个多项式的每一项乘另外一个多项式的每一项,再把所得的积相加求得,a+3b=-5,联立方程,解二元一次方程组,即可求出a与b的值;
(2)将a和b的值代入,根据多项式与多项式相乘的法则:多项式与多项式相乘,先用一个多项式的每一项乘另外一个多项式的每一项,再把所得的积相加进行计算即可求解.
20.【答案】(1)解:
所以
因为 为正整数
所以
所以
(2)解:图中甲长方形的周长为
所以该正方形的边长为
∴S-S1=(m+4)2-(m2+8m+7)=m2+8m+16-m2-8m-7=9.
所以所以这个常数为9.
【解析】【分析】(1)利用长方形的面积等于长乘以宽,分别列式求出S1和S2,再求出S1-S2,由m为正整数,可得到S1和S2的大小.
(2)求出甲图形中的长方形的周长,根据一正方形的周长和甲长方形的周长相等,可求出该正方形的边长,然后求出S-S1,即可得到这个常数.
21.【答案】(1);
(2)(a+b)(a-b)=a2-b2
(3)解:应用乘法公式得:
.
【解析】【解答】解:(1)图①中:大正方形的边长为a,小正方形的边长为b,
;
图②中:大正方形的边长为a,小正方形的边长为b,
阴影部分长方形的长为(a+b),宽为(a-b),
.
故答案为:;;
(2)由图可知,两图的阴影部分面积相等,故(a+b)(a-b)=a2-b2.
故答案为:(a+b)(a-b)=a2-b2;
【分析】(1)利用割补法可知,图①阴影部分面积可看成是大正方形面积减去小正方形面积,再利用正方形的面积公式表示出阴影部分面积;图②阴影部分面积可看出一个长方形,先求得长方形的长与宽,再表示出长方形的面积;
(2)图②的阴影部分面积是由图①的两个小长方形拼接而成的,故两图的阴影部分面积相等,据此可得乘法公式
(3)先利用平方差公式对括号内的整式进行因式分解,再进行有理数的混合运算即可得出答案.
22.【答案】(1)(a+b)2=(a-b)2+4ab
(2)解:由(a+b)2=(a-b)2+4ab,得(x-y)2=(x+y)2-4xy
=25-9
=16
(3)解:∵a2+b2=(a+b)2-2ab,
∴(2019-m)2+(m-2020)2
[(2019-m)+(m-2020)]2-2(2019-m)(m-2020)
=(-1)2-2(2019-m)(m-2020)
又∵(2019-m)2+(m-2020)2=7
∴7=1-2(2019-m)(m-2020)
(2019-m)(m-2020)=-3.
【解析】【解答】解:(1)由图2可知,大正方形的边长为(a+b),小正方形的边长为(a-b),大正方形的面积可以表示为(a+b)2或(a-b)2+4ab,因此有(a+b)2=(a-b)2+4ab
故答案为(a+b)2=(a-b)2+4ab
【分析】(1)由大面积=小面积之和,可以得出结果。
(2)利用(1)的等式(a+b)2=(a-b)2+4ab,可以得出结果。
(3)容易观察出隐含条件 (2019-m)+(m-2020)=-1,再利用完全平方公式,得出结果。
1 / 1
一、选择题(每题3分,共30分)
1.即空气中的细颗粒物,它的直径不超过0.0025毫米,以下用科学记数法表示数字0.0025正确的是( )
A. B. C. D.
2.下列运算正确的是( )
A. B. C. D.
3.下列整式中,属于完全平方式的是( )
A. B. C. D.
4.若,.则等于( )
A. B. C. D.0
5.如果m2+m=5,那么代数式 的值为( )
A.14 B.9 C.1 D.6
6.计算(-6x-5y)(5y-6x)的结果是( ).
A. B.
C. D.
7.若,则,的值分别是( )
A., B.,
C., D.,
8.如图①,在边长为a的正方形中剪去一个边长为b(b
C.(a+b)2=a2+2ab+b2 D.a2-b2=(a+b)(a-b)
9.若A=(2+1)(22+1)(24+1)(28+1)+1,则A的末位数字是( )
A.2 B.4 C.6 D.8
10.关于的多项式:,其中为正整数,若各项系数各不相同且均不为0,我们称这样的多项式为“亲缘多项式”.
①是“亲缘多项式”.
②若多项式和均为“亲缘多项式”,则也是“亲缘多项式”.
③多项式是“亲缘多项式”且.
④关于的多项式,若,,为正整数,则为“亲缘多项式”.
以上说法中正确的个数是( )
A.1 B.2 C.3 D.4
二、填空题(每题4分,共24分)
11.若 ,则 。
12.若 的乘积中不含 的一次项,则常数 .
13.若x2﹣mx+16是一个完全平方式,则m= .
14.如图,边长为6的正方形ABCD中放置两个长和宽分别为a,b的长方形,若长方形的周长为 16,面积为 15.75,则图中阴影部分的面积S = .
15.已知甲、乙两个长方形,它们的边长如图所示(为正整数),甲、乙的面积分别为,.
(1)与的大小关系为: (填“>”“=”或“<”);
(2)若满足的整数有且只有2个,则的值是 .
16.如果一个三位自然数的各数位上的数字互不相等且均不为0,满足,那么称这个三位数为“中庸数”.将“中庸数”的百位、个位数字交换位置,得到另一个“中庸数”,记.例如:.,.计算 ;若“中庸数”满足,其中为自然数1,2,3……,则该“中庸数”是 .
三、解答题(共8题,共66分)
17.已知.
(1)化简A;
(2)若,求A的值.
18.设 n 为正整数,且求 '的值。
19.小马和小睿两人共同计算--道整式乘法题:(3x+a)(2x+b),由于小马抄错了a的符号,得到的结果为6x2-17x+12;由于小睿漏抄了第二个多项式中x的系数,得到的结果为3x2-5x-12.
(1)求出a,b的值.
(2)请你计算出这道整式乘法题的正确结果.
20.如图,甲长方形的长为m+7,宽为m+1,面积为S1;乙长方形的长为m+4,宽为m+2,面积为S2.(m为正整数)
(1)试比较S1,S2的大小;
(2)现有一正方形,其周长与图中的甲长方形周长相等,试探究:该正方形面积S与图中的甲长方形面积S1的差(即S﹣S1)是一个常数,求出这个常数.
21.如图①,从边长为a的大正方形中剪掉一个边长为b的小正方形,将阴影部分沿线剪开,如图所示,拼成图②的长方形.
(1)请你表示出图①中阴影部分的面积 ;
请你表示出图②中阴影部分的面 ;
(2)比较两图的阴影部分面积,可以得到乘法公式: ;
(3)请应用公式计算:.
22.一个宽为a、长为4b的长方形如图1所示,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成一个“回形”正方形(如图2)。
(1)观察图2,请你用等式表示(a+b)2,(a-b)2,
ab之间的数量关系: 。
(2)根据(1)中的结论,如果x+y=5,xy=,求代数式(x-y)2的值。
(3)如果(2019-m)2+(m-2020)2=7。
求(2019-m)(m-2020)的值。
答案解析部分
1.【答案】D
【解析】【解答】解:0.0025用科学记数法表示为,故D正确.
故答案为:D.
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正整数;当原数的绝对值<1时,n是负整数,据此判断即可.
2.【答案】B
【解析】【解答】A. ,不符合题意;
B. ,符合题意;
C. ,不符合题意;
D. ,不符合题意
故答案为:B
【分析】根据同底幂乘、除法,乘方运算以及加减运算规则分别求解判断.
3.【答案】D
4.【答案】C
【解析】【解答】解: ∵,.
∴=a3m÷a2n=(am)3÷(an)2=33÷22=.
故答案为:C.
【分析】利用同底数幂的除法、幂的乘方将原式化为(am)3÷(an)2,再代入计算即可.
5.【答案】A
【解析】【解答】
∵m2+m=5,
∴原式 ,
故答案为:A.
【分析】先化简代数式,再将m2+m=5代入求解即可。
6.【答案】A
【解析】【解答】解: (-6x-5y)(5y-6x)
= -(5y+6x)(5y-6x)
=-[(5y)2-(6x)2]
=-(25y2-36x2)
=36x2-25y2.
故答案为:A.
【分析】从第一个因式中提出一个负号并将括号内的项交换位置变形成平方差公式的标准形式,进而利用平方差公式计算,最后去括号即可得出答案.
7.【答案】A
【解析】【解答】∵,,
∴,,
故答案为:A.
【分析】先利用多项式乘多项式的计算方法展开,再利用待定系数法求出a、b的值即可。
8.【答案】D
【解析】【解答】解:∵左图中阴影部分的面积是a2-b2,右图中梯形的面积是 (2a+2b)(a-b)=(a+b)(a-b),
∴a2-b2=(a+b)(a-b).
故答案为:D.
【分析】根据左图中阴影部分的面积是a2-b2,右图中梯形的面积是 (2a+2b)(a-b)=(a+b)(a-b),利用面积相等即可解答.
9.【答案】C
【解析】【解答】解:∵A=(2+1)(22+1)(24+1)(28+1)+1,
∴A=(2-1)(2+1)(22+1)(24+1)(28+1)+1,
=(22-1)(22+1)(24+1)(28+1)+1,
=(24-1)(24+1)(28+1)+1,
=(28-1)(28+1)+1,
=216-1+1,
=216.
∵21=2,22=4,23=8,24=16,25=32,
∴末位数字以4为周期,
∴16=4×4,
∴216的末位数字是6,
∴原式末位数字是6.
故答案为:C.
【分析】将原式转化成A=(2-1)(2+1)(22+1)(24+1)(28+1)+1,利用平方差公式计算即可得A=216,再以2的幂的末位数字以4为周期,由16=4×4得原式末位数字.
10.【答案】B
【解析】【解答】解:①=4x2-4x+1,且各项系数各不相同且均不为0,
∴是" 亲缘多项式 ",故①正确;
② 原式,无法确定各项系数各不相同且均不为0 ,
∴原式不是" 亲缘多项式 ",故②不正确;
③∵是"亲缘多项式",
∴b4=16,b2=24,b0=1
∴b4+b2+b0=41,故③正确;
④当a=1,b=-1时,n=4时,
(x-1)4=x4-4x3+6x2-4x+1,其中三次项系数与一次项系数相同,
∴(x-1)4不是" 亲缘多项式 ",故④不正确;
∴ 正确的个数是2个;
故答案为:B.
【分析】①利用完全平方公式将展开,根据" 亲缘多项式 "的定义判断即可;
②先合并同类项,再根据" 亲缘多项式 "的定义判断即可;
③将(2x-1)4展开,根据" 亲缘多项式 "的定义判断即可;
④用特殊值法进行判断即可.
11.【答案】3或1.
【解析】【解答】解 :① : 得:t-3=0,解得t=3,
② ;t-2=1,t=3;
③t-2=-1,t=1;
故答案为:3或1.
【分析】此题分三类讨论,①根据零指数的意义得出t-3=0,解得t=3,②根据1的任何次幂=1得出t-2=1,t=3;③根据-1的偶次幂等于1得出t-2=-1,t=1;综上所述从而得出答案。
12.【答案】6
【解析】【解答】∵ 的乘积中不含 的一次项,
∴ = 中
∴
故答案为:6.
【分析】直接利用多项式乘法去括号,进而得出一次项系数为0,求解即可.
13.【答案】
【解析】【解答】解:∵ x2﹣mx+16是一个完全平方式
∴x2﹣mx+16=(x±4)2
∴x2﹣mx+16=x2±8x+16
∴m=±8
故答案为:±8
【分析】根据完全平方公式的结构特点,可知x2﹣mx+16=(x±4)2,将等式右边的括号展开,就可得到m的值。注意:完全平方公式有两个。
14.【答案】12.5
【解析】【解答】解:由题可得:
即
故答案为:12.5.
【分析】根据长方形的周长为16,面积为15.75,得到结合图形用含a,b的式子表示S1,S2,S3,利用完全平方公式计算出的值,从而求解.
15.【答案】(1)
(2)1011
【解析】【解答】解:(1)根据图示知:S1=(m+4)(m+2)=m2+6m+8,S2=(m+7)(m+1)=m2+8m+7,
∴S1-S2=(m2+6m+8)-(m2+8m+7)=-2m+1,
∵m为正整数,
∴m≥1,
∴-2m≤-2,
∴-2m+1≤-2+1,
∴-2m+1<0,
∴S1-S2<0,
∴S1<S2;
故答案为:<;
(2)由(1)知:丨S2-S1丨=丨-2m+1丨=2m-1,
∵丨S2-S1丨<n≤2023的整数n只有两个,
∴整数n为:2022,2023,
∴丨S2-S1丨=2021,
∴2m-1=2021,
∴m=1011,
故答案为:1011.
【分析】(1)首先根据长方形的面积计算公式求得S1=m2+6m+8和S2=m2+8m+7,然后计算S1-S2=-2m+1,根据m为正整数,可判断S1-S2<0,进而得出S1<S2的结论;
(2)由(1)知,-2m+1<0,可得丨S2-S1丨=2m-1,根据S2-S1丨<n≤2023的整数n只有两个,可得整数n为:2022,2023,故而得出丨S2-S1丨=2021,即2m-1=2021,解方程,即可求出m的值。
16.【答案】2;121或484或583
【解析】【解答】解:由题意得:,
因为,,
,
均为完全平方数,
即,为完全平方数,且为偶数,可能为4、16、36、64、100等,
则,可能为0、2、8、18、50等,
因为,,
所以,只可能为0,2,8,
可得当时,或;当时,,
所以或或,,
可得或484或583.
故答案为:2;121或484或583
【分析】先根据题意结合整式的混合运算得到,均为完全平方数,进而结合题意即可得到,可能为0、2、8、18、50等,从而即可求出或或,,再计算m即可求解。
17.【答案】(1)解:;
(2)解:∵,
∴,
∴
.
18.【答案】解:∵
∴
【解析】【分析】根据积的乘方进行化简,并整体代入计算即可.
19.【答案】(1)解:∵小马抄错了a的符号,得到的结果为6x2-17x+12,
∴
即;
∵小睿漏抄了第二个多项式中x的系数,得到的结果为3x2-5x-12,
∴(3x+a)(x+b)=3x2-5x-12,
即a+3b=-5,
故可得,
解得.
(2)解:∵a=4,b=-3,
∴.
【解析】【分析】(1)分别根据多项式与多项式相乘的法则:多项式与多项式相乘,先用一个多项式的每一项乘另外一个多项式的每一项,再把所得的积相加求得,a+3b=-5,联立方程,解二元一次方程组,即可求出a与b的值;
(2)将a和b的值代入,根据多项式与多项式相乘的法则:多项式与多项式相乘,先用一个多项式的每一项乘另外一个多项式的每一项,再把所得的积相加进行计算即可求解.
20.【答案】(1)解:
所以
因为 为正整数
所以
所以
(2)解:图中甲长方形的周长为
所以该正方形的边长为
∴S-S1=(m+4)2-(m2+8m+7)=m2+8m+16-m2-8m-7=9.
所以所以这个常数为9.
【解析】【分析】(1)利用长方形的面积等于长乘以宽,分别列式求出S1和S2,再求出S1-S2,由m为正整数,可得到S1和S2的大小.
(2)求出甲图形中的长方形的周长,根据一正方形的周长和甲长方形的周长相等,可求出该正方形的边长,然后求出S-S1,即可得到这个常数.
21.【答案】(1);
(2)(a+b)(a-b)=a2-b2
(3)解:应用乘法公式得:
.
【解析】【解答】解:(1)图①中:大正方形的边长为a,小正方形的边长为b,
;
图②中:大正方形的边长为a,小正方形的边长为b,
阴影部分长方形的长为(a+b),宽为(a-b),
.
故答案为:;;
(2)由图可知,两图的阴影部分面积相等,故(a+b)(a-b)=a2-b2.
故答案为:(a+b)(a-b)=a2-b2;
【分析】(1)利用割补法可知,图①阴影部分面积可看成是大正方形面积减去小正方形面积,再利用正方形的面积公式表示出阴影部分面积;图②阴影部分面积可看出一个长方形,先求得长方形的长与宽,再表示出长方形的面积;
(2)图②的阴影部分面积是由图①的两个小长方形拼接而成的,故两图的阴影部分面积相等,据此可得乘法公式
(3)先利用平方差公式对括号内的整式进行因式分解,再进行有理数的混合运算即可得出答案.
22.【答案】(1)(a+b)2=(a-b)2+4ab
(2)解:由(a+b)2=(a-b)2+4ab,得(x-y)2=(x+y)2-4xy
=25-9
=16
(3)解:∵a2+b2=(a+b)2-2ab,
∴(2019-m)2+(m-2020)2
[(2019-m)+(m-2020)]2-2(2019-m)(m-2020)
=(-1)2-2(2019-m)(m-2020)
又∵(2019-m)2+(m-2020)2=7
∴7=1-2(2019-m)(m-2020)
(2019-m)(m-2020)=-3.
【解析】【解答】解:(1)由图2可知,大正方形的边长为(a+b),小正方形的边长为(a-b),大正方形的面积可以表示为(a+b)2或(a-b)2+4ab,因此有(a+b)2=(a-b)2+4ab
故答案为(a+b)2=(a-b)2+4ab
【分析】(1)由大面积=小面积之和,可以得出结果。
(2)利用(1)的等式(a+b)2=(a-b)2+4ab,可以得出结果。
(3)容易观察出隐含条件 (2019-m)+(m-2020)=-1,再利用完全平方公式,得出结果。
1 / 1
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
