5.5分式方程(2) 课件(共11张PPT)浙教版七年级数学下册
文档属性
| 名称 | 5.5分式方程(2) 课件(共11张PPT)浙教版七年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 289.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-18 17:54:10 | ||
图片预览




文档简介
(共11张PPT)
5.5 分式方程(2)
第5章 分式
浙教版 七年级下册
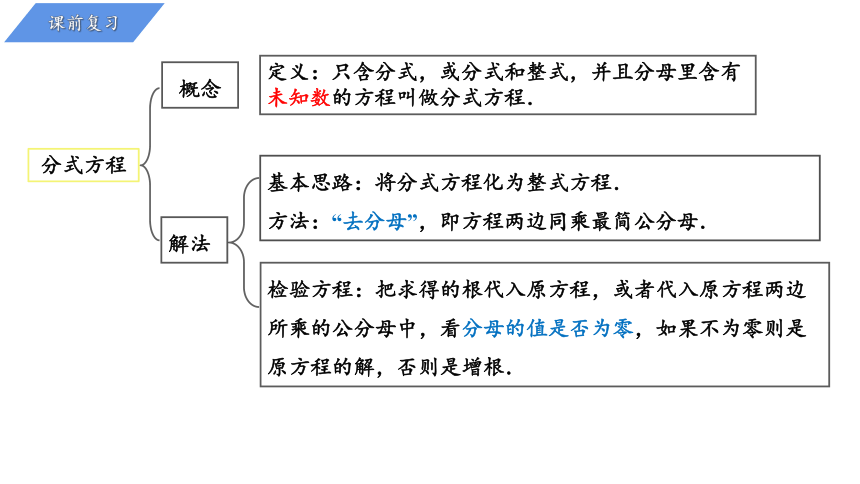
课前复习
分式方程
概念
解法
定义:只含分式,或分式和整式,并且分母里含有未知数的方程叫做分式方程.
基本思路:将分式方程化为整式方程.
方法:“去分母”,即方程两边同乘最简公分母.
检验方程:把求得的根代入原方程,或者代入原方程两边所乘的公分母中,看分母的值是否为零,如果不为零则是原方程的解,否则是增根.
课前复习
(1)若方程有增根,且增根为x=1,求m的值.
(2)若方程有增根,求m的值.
(3)若方程无解,求m的值.
解:方程两边同乘____________,得_____________________.
去括号,得_______________________.
移项,得______________________.
合并同类项,得________________.
新知探究
【例1】某地水稻种植基地在A,B两个面积相同的试验田里种植不同品种的水稻,分别收获16.8吨和13.2吨。已知A试验田的水稻比B试验田的水稻每公顷多收获3吨,分别求A、B两个试验田的水稻产量.
解:设A试验田产量为每公顷x吨,则B试验田产量为每公顷(x-3)吨.
由题意,得
解这个方程,得x=14
经检验,x=14是所列方程的根,且符合题意.
所以B试验田产量为每公顷为14-3=11(吨)
答:A试验田的产量是每公顷14吨,B试验田的产量是每公顷11吨.
新知探究
列分式方程解应用题的一般步骤
(1)审:分析题意,找出数量关系和相等关系.
(2)设:选择恰当的未知数,注意单位和语言完整.
(3)列:根据数量和相等关系,正确列出代数式和方程.
(4)解:求出所列方程的解.
(5)验:要二次检验.
二次检验是:
(1)是不是所列方程的解;
(2)是否满足实际意义.
(6)答:注意单位和语言完整.且答案要生活化.
【例2】甲、乙两人每小时共能做35个零件。甲、乙两人同时开始工作,当甲做了90个零件时,乙做了120个.问甲、乙每小时各做多少个零件?
解:设甲每时能做x个零件,则乙每时能做 个零件.
(35-x)
由题意,得
90
x
120
35-x
=
解得 x=15
经检验, x=15是所列方程的根,且符合题意
所以乙每小时能做35-x=35-15=20
答:甲每时能做15个,乙每时能做20个.
例题讲解
【例3】甲,乙二人同时从张庄出发,步行15千米到李庄,甲比乙每小时多走1千米,结果比乙早到半小时,二人每小时各走几千米?
解:设乙每小时走x千米,则甲每小时走(x+1)千米.
例题讲解
例题讲解
【例4】照相机成像应用了一个重要原理,即 (v≠f ),问在 f、v已知的情况下,怎样确定物体到镜头的距离u?
【分析】本题就是把f、v看成已知数,u看成未知数,解关于u的分式方程.
例题讲解
例题讲解
【例6】
课堂总结
列分式方程解应用题的一般步骤
(1)审:分析题意,找出数量关系和相等关系.
(2)设:选择恰当的未知数,注意单位和语言完整.
(3)列:根据数量和相等关系,正确列出代数式和方程.
(4)解:求出所列方程的解.
(5)验:要二次检验.
二次检验是:
(1)是不是所列方程的解;
(2)是否满足实际意义.
(6)答:注意单位和语言完整.且答案要生活化.
5.5 分式方程(2)
第5章 分式
浙教版 七年级下册
课前复习
分式方程
概念
解法
定义:只含分式,或分式和整式,并且分母里含有未知数的方程叫做分式方程.
基本思路:将分式方程化为整式方程.
方法:“去分母”,即方程两边同乘最简公分母.
检验方程:把求得的根代入原方程,或者代入原方程两边所乘的公分母中,看分母的值是否为零,如果不为零则是原方程的解,否则是增根.
课前复习
(1)若方程有增根,且增根为x=1,求m的值.
(2)若方程有增根,求m的值.
(3)若方程无解,求m的值.
解:方程两边同乘____________,得_____________________.
去括号,得_______________________.
移项,得______________________.
合并同类项,得________________.
新知探究
【例1】某地水稻种植基地在A,B两个面积相同的试验田里种植不同品种的水稻,分别收获16.8吨和13.2吨。已知A试验田的水稻比B试验田的水稻每公顷多收获3吨,分别求A、B两个试验田的水稻产量.
解:设A试验田产量为每公顷x吨,则B试验田产量为每公顷(x-3)吨.
由题意,得
解这个方程,得x=14
经检验,x=14是所列方程的根,且符合题意.
所以B试验田产量为每公顷为14-3=11(吨)
答:A试验田的产量是每公顷14吨,B试验田的产量是每公顷11吨.
新知探究
列分式方程解应用题的一般步骤
(1)审:分析题意,找出数量关系和相等关系.
(2)设:选择恰当的未知数,注意单位和语言完整.
(3)列:根据数量和相等关系,正确列出代数式和方程.
(4)解:求出所列方程的解.
(5)验:要二次检验.
二次检验是:
(1)是不是所列方程的解;
(2)是否满足实际意义.
(6)答:注意单位和语言完整.且答案要生活化.
【例2】甲、乙两人每小时共能做35个零件。甲、乙两人同时开始工作,当甲做了90个零件时,乙做了120个.问甲、乙每小时各做多少个零件?
解:设甲每时能做x个零件,则乙每时能做 个零件.
(35-x)
由题意,得
90
x
120
35-x
=
解得 x=15
经检验, x=15是所列方程的根,且符合题意
所以乙每小时能做35-x=35-15=20
答:甲每时能做15个,乙每时能做20个.
例题讲解
【例3】甲,乙二人同时从张庄出发,步行15千米到李庄,甲比乙每小时多走1千米,结果比乙早到半小时,二人每小时各走几千米?
解:设乙每小时走x千米,则甲每小时走(x+1)千米.
例题讲解
例题讲解
【例4】照相机成像应用了一个重要原理,即 (v≠f ),问在 f、v已知的情况下,怎样确定物体到镜头的距离u?
【分析】本题就是把f、v看成已知数,u看成未知数,解关于u的分式方程.
例题讲解
例题讲解
【例6】
课堂总结
列分式方程解应用题的一般步骤
(1)审:分析题意,找出数量关系和相等关系.
(2)设:选择恰当的未知数,注意单位和语言完整.
(3)列:根据数量和相等关系,正确列出代数式和方程.
(4)解:求出所列方程的解.
(5)验:要二次检验.
二次检验是:
(1)是不是所列方程的解;
(2)是否满足实际意义.
(6)答:注意单位和语言完整.且答案要生活化.
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
