浙教版七年级下册1.4 平行线的性质 课件(21张PPT)
文档属性
| 名称 | 浙教版七年级下册1.4 平行线的性质 课件(21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 08:32:54 | ||
图片预览





文档简介
(共21张PPT)
1.4平行线的性质(第1课时)
单击此处添加副标题
目录
01
4平行线的性质(第1课时)
单击此处添加文本具体内容
02
复习旧知,厘清学路
单击此处添加文本具体内容
03
动手操作,探究性质
单击此处添加文本具体内容
04
单击此处添加文本具体内容
学程导航
05
问题解决,学以致用
单击此处添加文本具体内容
06
单击此处添加文本具体内容
学程回顾,盘点收获
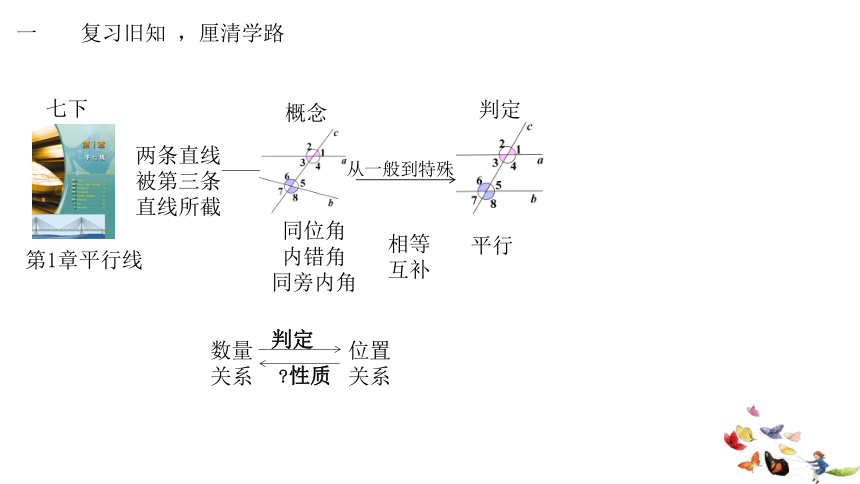
一 复习旧知 ,厘清学路
概念
邻补角
对顶角
性质
互补
相等
从一般到特殊
特例
垂直
数量
关系
位置
关系
判定
性质
两条直线
相交
6.9直线的相交
七上
一 复习旧知 ,厘清学路
概念
同位角
内错角
同旁内角
从一般到特殊
相等
互补
平行
判定
数量
关系
位置
关系
判定
性质
两条直线
被第三条
直线所截
七下
第1章平行线
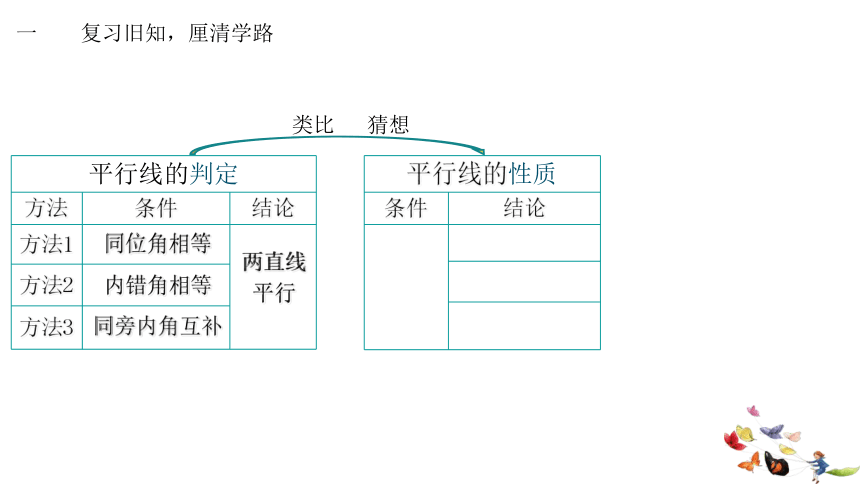
一 复习旧知,厘清学路
平行线的判定 方法 条件 结论
方法1
方法2 方法3 平行线的性质 条件 结论
类比 猜想
同位角相等
内错角相等
同旁内角互补
两直线
平行
同位角相等
内错角相等
同旁内角互补
两直线
平行
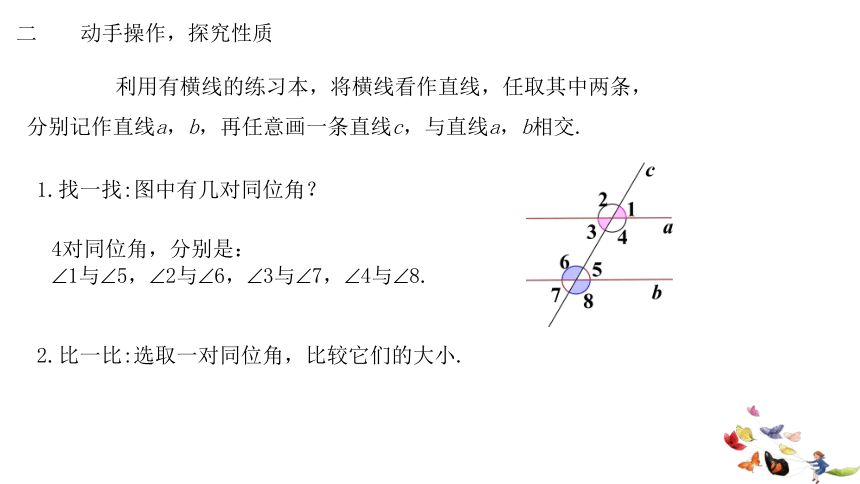
二 动手操作,探究性质
利用有横线的练习本,将横线看作直线,任取其中两条,
分别记作直线a,b,再任意画一条直线c,与直线a,b相交.
1.找一找:图中有几对同位角?
4对同位角,分别是:
1与 5, 2与 6, 3与 7, 4与 8.
2.比一比:选取一对同位角,比较它们的大小.
二 动手操作,探究性质
方法2:叠合法
1= 5
a∥b
∠1=65°
∠5=65°
方法1:度量法
(量角器)
(透明塑料板、折叠尺等)
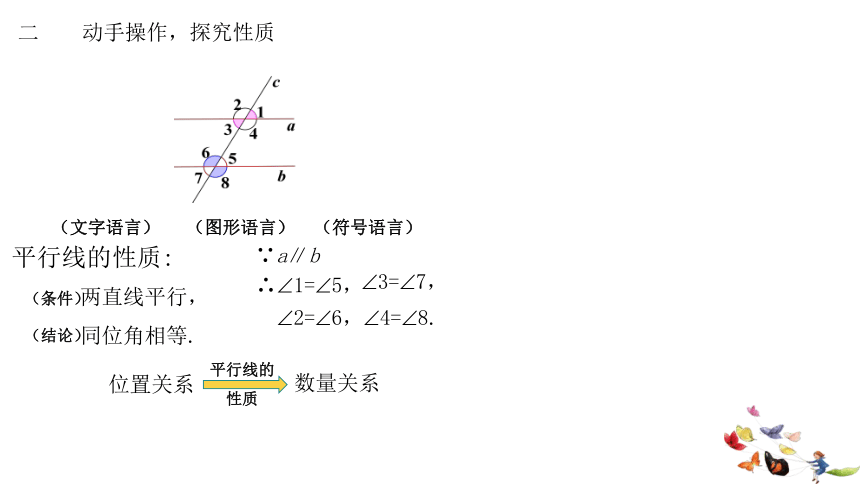
二 动手操作,探究性质
3.变一变:改变直线c的位置,上述结论还成立吗
4.验一验:几何画板验证.
利用有横线的练习本,将横线看作直线,任取其中两条,
分别记作直线a,b,再任意画一条直线c,与直线a,b相交.
(条件)
(结论)
(文字语言)
(图形语言)
(符号语言)
∴ 1= 5,
∵a∥b
平行线的性质:
两直线平行,
同位角相等.
数量关系
位置关系
平行线的 性质
2= 6,
3= 7,
4= 8.
二 动手操作,探究性质
1
2
A
B
C
D
例1.如图,梯子的各条横档互相平行, 1=100°,求 2的度数.
3
解:∵AB//CD
∴ 3= 1=100°
∴ 2=100° 3
=180° 100°
=80°
(两直线平行,同位角相等)
(由因寻果)
实物图
A
B
C
D
1
2
几何图
综合法
三 问题解决,学以致用
AB//CD
平行线的性质
3= 1=100°
平角的意义
2=100° 3
已知,如图,
AB//CD, 1=100°
求 2的度数.
2
(执果索因)
分析法
实物图
2
例1.如图,梯子的各条横档互相平行, 1=100°,求 2的度数.
四 问题解决,学以致用
1(已知)
平行线的性质
3
平角的意义
4
平行线的性质
1(已知)
平角的意义
1
2
A
B
C
D
1
2
几何图
3
4
已知,如图,
AB//CD, 1=100°,
求 2的度数.
实物图
几何图
明确求什么?可转化什么来求?
关键是转化
转化依据:基本事实 定义 定理等
分析
【解题小结】
四 问题解决,学以致用
AB//CD
平行线的性质
3= 1=100°
平角的意义
2=100° 3
1(已知)
2
3
平行线的性质
平角的意义
4
1(已知)
平行线的性质
平角的意义
2
1
2
A
B
C
D
1
2
3
4
三线八角
角的
转化
平行线
的性质
例2.如图,已知 1= 2.若直线b⊥m,则直线a⊥m.请说明理由.
1= 2
b⊥m
(已知),
∴ 4= 3=90°
(已知),
(同位角相等,两直线平行).
(两直线平行,同位角相等).
∵ 1= 2
∴a∥b
解:∵b⊥m
∴ 3=90°
(垂直的意义).
∴a⊥m
(垂直的定义).
a⊥m
3=90°
垂直的定义
a∥b
平行线的判定
4=90°
垂直的意义
平行线的性质
四 问题解决,学以致用
a
b
m
n
1
2
4
3
分析法、综合法交替使用
练习.已知:如图,AB∥DE, B= E,试说明BC∥EF.
AB∥DE
B= 1
B= E
1= E
平行线的判定
等量代换
1
BC∥EF
平行线的性质
(已知),
(同位角相等,两直线平行).
(两直线平行,同位角相等).
∵ B= E
∴ 1= E
解:∵AB∥DE
(已知),
∴ B= 1
∴BC∥EF
(等量代换),
A
E
B
F
C
D
G
四 问题解决,学以致用
变式1.已知:如图,AB∥DE,BC∥EF,试说明 B= E.
B= E
等量代换
1
(两直线平行,同位角相等)
∴ B= E
解:∵AB∥DE,BC∥EF
∴ B= 1, 1= E
A
E
B
F
C
D
G
AB∥DE
BC∥EF
B= 1
1= E
平行线的性质
平行线的性质
四 问题解决,学以致用
变式2.已知:如图,AB∥DE,BC∥EF, B与 E还相等吗?
(两直线平行,同位角相等)
∴ B= DEF
∵AB∥DE,BC∥EF
∴ B= DGC, DGC= DEF
A
B
C
E
F
D
解: B= E.理由如下:
延长DE交BC于点G
G
E
F
D
A
B
C
E
F
D
A
B
C
四 问题解决,学以致用
A
B
C
E
F
D
G
E
F
D
A
B
C
E
F
D
A
B
C
四 问题解决,学以致用
三线八角
角的
转化
添截线或平行
平行线
的性质
变式3.已知:如图,AB∥DE,BC∥EF, B与 E还相等吗?
(两直线平行,同位角相等)
∴ B= E
∵AB∥DE,BC∥EF
∴ B= 1, E= 2
A
B
C
E
F
D
解: B= E.理由如下:
四 问题解决,学以致用
1
2
∵ 1= 2
A
B
C
E
F
D
四 问题解决,学以致用
E
F
D
A
B
C
A
E
B
F
C
D
G
变化中探寻不变,揭露问题的本质
六 学程回顾 ,盘点收获
概念
特例
从一般到特殊
性质
从一般到特殊
平行线的判定
判定1:同位角相等,两直线平行
判定2:内错角相等,两直线平行
判定3:同旁内角互补,两直线平行
类比学行线的性质
类比
探究过程
性质1:两直线平行,同位角相等
?
位置关系
数量关系
判定
思想
方法
类比
转化
猜想
验证
归纳
应用
基于本节课的学习历程,你认为下一节课 我们要研究什么内容呢?又将按照怎样的顺序或思路展开研究呢?不妨试着写一写.
作业:详见作业单 .
七 课后作业,及时巩固
1.4平行线的性质(第1课时)
单击此处添加副标题
目录
01
4平行线的性质(第1课时)
单击此处添加文本具体内容
02
复习旧知,厘清学路
单击此处添加文本具体内容
03
动手操作,探究性质
单击此处添加文本具体内容
04
单击此处添加文本具体内容
学程导航
05
问题解决,学以致用
单击此处添加文本具体内容
06
单击此处添加文本具体内容
学程回顾,盘点收获
一 复习旧知 ,厘清学路
概念
邻补角
对顶角
性质
互补
相等
从一般到特殊
特例
垂直
数量
关系
位置
关系
判定
性质
两条直线
相交
6.9直线的相交
七上
一 复习旧知 ,厘清学路
概念
同位角
内错角
同旁内角
从一般到特殊
相等
互补
平行
判定
数量
关系
位置
关系
判定
性质
两条直线
被第三条
直线所截
七下
第1章平行线
一 复习旧知,厘清学路
平行线的判定 方法 条件 结论
方法1
方法2 方法3 平行线的性质 条件 结论
类比 猜想
同位角相等
内错角相等
同旁内角互补
两直线
平行
同位角相等
内错角相等
同旁内角互补
两直线
平行
二 动手操作,探究性质
利用有横线的练习本,将横线看作直线,任取其中两条,
分别记作直线a,b,再任意画一条直线c,与直线a,b相交.
1.找一找:图中有几对同位角?
4对同位角,分别是:
1与 5, 2与 6, 3与 7, 4与 8.
2.比一比:选取一对同位角,比较它们的大小.
二 动手操作,探究性质
方法2:叠合法
1= 5
a∥b
∠1=65°
∠5=65°
方法1:度量法
(量角器)
(透明塑料板、折叠尺等)
二 动手操作,探究性质
3.变一变:改变直线c的位置,上述结论还成立吗
4.验一验:几何画板验证.
利用有横线的练习本,将横线看作直线,任取其中两条,
分别记作直线a,b,再任意画一条直线c,与直线a,b相交.
(条件)
(结论)
(文字语言)
(图形语言)
(符号语言)
∴ 1= 5,
∵a∥b
平行线的性质:
两直线平行,
同位角相等.
数量关系
位置关系
平行线的 性质
2= 6,
3= 7,
4= 8.
二 动手操作,探究性质
1
2
A
B
C
D
例1.如图,梯子的各条横档互相平行, 1=100°,求 2的度数.
3
解:∵AB//CD
∴ 3= 1=100°
∴ 2=100° 3
=180° 100°
=80°
(两直线平行,同位角相等)
(由因寻果)
实物图
A
B
C
D
1
2
几何图
综合法
三 问题解决,学以致用
AB//CD
平行线的性质
3= 1=100°
平角的意义
2=100° 3
已知,如图,
AB//CD, 1=100°
求 2的度数.
2
(执果索因)
分析法
实物图
2
例1.如图,梯子的各条横档互相平行, 1=100°,求 2的度数.
四 问题解决,学以致用
1(已知)
平行线的性质
3
平角的意义
4
平行线的性质
1(已知)
平角的意义
1
2
A
B
C
D
1
2
几何图
3
4
已知,如图,
AB//CD, 1=100°,
求 2的度数.
实物图
几何图
明确求什么?可转化什么来求?
关键是转化
转化依据:基本事实 定义 定理等
分析
【解题小结】
四 问题解决,学以致用
AB//CD
平行线的性质
3= 1=100°
平角的意义
2=100° 3
1(已知)
2
3
平行线的性质
平角的意义
4
1(已知)
平行线的性质
平角的意义
2
1
2
A
B
C
D
1
2
3
4
三线八角
角的
转化
平行线
的性质
例2.如图,已知 1= 2.若直线b⊥m,则直线a⊥m.请说明理由.
1= 2
b⊥m
(已知),
∴ 4= 3=90°
(已知),
(同位角相等,两直线平行).
(两直线平行,同位角相等).
∵ 1= 2
∴a∥b
解:∵b⊥m
∴ 3=90°
(垂直的意义).
∴a⊥m
(垂直的定义).
a⊥m
3=90°
垂直的定义
a∥b
平行线的判定
4=90°
垂直的意义
平行线的性质
四 问题解决,学以致用
a
b
m
n
1
2
4
3
分析法、综合法交替使用
练习.已知:如图,AB∥DE, B= E,试说明BC∥EF.
AB∥DE
B= 1
B= E
1= E
平行线的判定
等量代换
1
BC∥EF
平行线的性质
(已知),
(同位角相等,两直线平行).
(两直线平行,同位角相等).
∵ B= E
∴ 1= E
解:∵AB∥DE
(已知),
∴ B= 1
∴BC∥EF
(等量代换),
A
E
B
F
C
D
G
四 问题解决,学以致用
变式1.已知:如图,AB∥DE,BC∥EF,试说明 B= E.
B= E
等量代换
1
(两直线平行,同位角相等)
∴ B= E
解:∵AB∥DE,BC∥EF
∴ B= 1, 1= E
A
E
B
F
C
D
G
AB∥DE
BC∥EF
B= 1
1= E
平行线的性质
平行线的性质
四 问题解决,学以致用
变式2.已知:如图,AB∥DE,BC∥EF, B与 E还相等吗?
(两直线平行,同位角相等)
∴ B= DEF
∵AB∥DE,BC∥EF
∴ B= DGC, DGC= DEF
A
B
C
E
F
D
解: B= E.理由如下:
延长DE交BC于点G
G
E
F
D
A
B
C
E
F
D
A
B
C
四 问题解决,学以致用
A
B
C
E
F
D
G
E
F
D
A
B
C
E
F
D
A
B
C
四 问题解决,学以致用
三线八角
角的
转化
添截线或平行
平行线
的性质
变式3.已知:如图,AB∥DE,BC∥EF, B与 E还相等吗?
(两直线平行,同位角相等)
∴ B= E
∵AB∥DE,BC∥EF
∴ B= 1, E= 2
A
B
C
E
F
D
解: B= E.理由如下:
四 问题解决,学以致用
1
2
∵ 1= 2
A
B
C
E
F
D
四 问题解决,学以致用
E
F
D
A
B
C
A
E
B
F
C
D
G
变化中探寻不变,揭露问题的本质
六 学程回顾 ,盘点收获
概念
特例
从一般到特殊
性质
从一般到特殊
平行线的判定
判定1:同位角相等,两直线平行
判定2:内错角相等,两直线平行
判定3:同旁内角互补,两直线平行
类比学行线的性质
类比
探究过程
性质1:两直线平行,同位角相等
?
位置关系
数量关系
判定
思想
方法
类比
转化
猜想
验证
归纳
应用
基于本节课的学习历程,你认为下一节课 我们要研究什么内容呢?又将按照怎样的顺序或思路展开研究呢?不妨试着写一写.
作业:详见作业单 .
七 课后作业,及时巩固
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
