初中数学浙教版七年级下册第二章 二元一次方程组 小结课件(16张PPT)
文档属性
| 名称 | 初中数学浙教版七年级下册第二章 二元一次方程组 小结课件(16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 258.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 08:51:47 | ||
图片预览






文档简介
(共16张PPT)
二元一次方程组(复习)
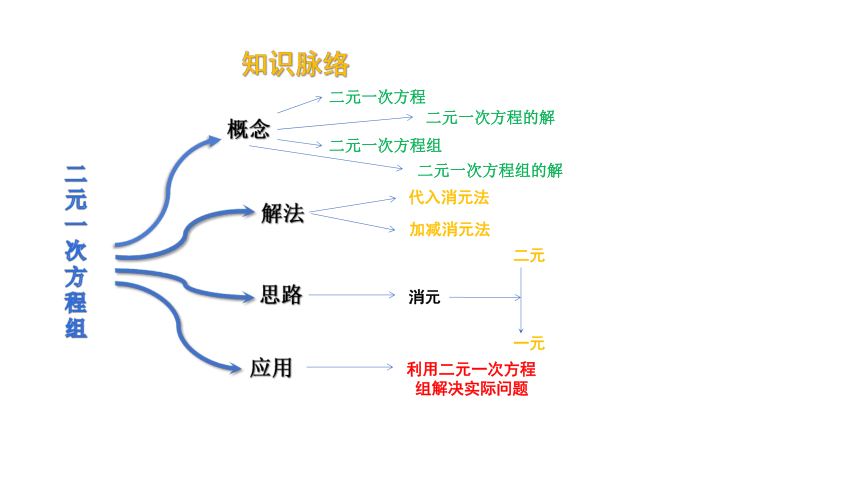
知识脉络
二
元
一
次
方
程
组
概念
二元一次方程
二元一次方程的解
二元一次方程组
二元一次方程组的解
解法
代入消元法
加减消元法
思路
消元
二元
一元
应用
利用二元一次方程
组解决实际问题
知识回顾
1.概念
(1)什么是二元一次方程?什么是二元一次方程的解?
答:含有两个未知数,并且所含未知数的项的次数都是
1的方程叫做二元一次方程,能使二元一次方程左右两边
相等的一对值叫做二元一次方程的一个解.
(2)什么是二元一次方程组?什么是二元一次方程组的解?
答:含有两个未知数的两个一次方程组成的方程组叫做二
元一次方程组.二元一次方程组中两个方程的公共解叫做二
元一次方程组的解.
小试牛刀
下列方程中是二元一次方程的是( )
A.x=2y B.x+2y=z C.xy+1=0 D.
2.下列方程组属于二元一次方程组的是( )
A. B.
C. D.
A
D
3.若方程xm+2+4y3n-2=4是关于x,y的二元一次方程,
则(2m+n)2023= .
4.若 是方程ax+by=3的解,则2a+4b+5= .
5. 若方程组 的解为 , 则a+b的
值为 .
m+2=1
3n-2=1
解得
m=-1
n=1
2m+n=-1
代入
(2m+n)2023 =-1
-1
a+2b=3
代入
2a+4b=6
×2
2a+4b+5=11
+5
11
代入
解得
a+b =2-1=1
代入
1
知识回顾
2.解法
解二元一次方程组的基本思想是什么?
二元一次方程组
一元一次方程
消元
化归
怎样解二元一次方程组呢?
代入消元法和加减消元法
典例精解
例1 解方程组:
(1) (2)
解:把①代入②,得x+x+1=5
解得x=2
把x=2代入①,得y=3
所以方程组的解为
解:①+②,得4x=8
解得x=2
把x=2代入①,得2+2y=9
解得y=
所以方程组的解为
典例精解
例2 解方程组:
(1) (2)
解:由②,得3x+2y=15③,
由①,得y=5-4x,
把y=5-4x代入③,
得3x+2(5-4x)=15
解得x=-1,
把x=-1代入y=5-4x,得y=9
所以方程组的解为
解:由①,得2x-3y=9 ③ ,
由②,得2x-y=3④,
③-④ ,得-2y=6,即y=-3,
把y=-3代入④ ,得2x-(-3)=3,
解得x=0,
所以方程组的解为
典例精解
例3 解方程组:
解:由②-①,得3(x-y)=6 ,解得x-y=2③,
得新方程组
解得:
所以方程组的解为
把x-y=2代入①,得x+y= ④,
小试牛刀
6.解方程组:
(1) (2)
(3) (4)
请按暂停,用5~10分钟时间解完上述题目,再继续.
小试牛刀
6.解方程组:
(1) (2)
(3) (4)
你解对了吗?如果解错了,请找一找错在哪里.
知识回顾
3.三元一次方程组的解法
三元一次方程组
一元一次方程
消元
化归
二元一次方程组
消元
化归
典例精解
例4 解方程组:
解:由①-②,得-2b=4,解得b=-2 ,
把b=-2分别代入① ,③得
解得a=1,c=-3
所以方程组的解为
知识回顾
4.二元一次方程组的应用
典例精解
例5 端午临仲夏,时清日复长.“临近端午节,一网红门店接
到一份粽子订单,立即决定由甲、乙两组加工完成.已知甲、
乙两组加工一天共生产350袋粽子,甲组加工2天比乙组加工1
天多生产250袋粽子.
(1)求甲、乙两组平均每天各能加工多少袋粽子?
(2)已知这份粽子订单为1700袋,若甲、乙两组共用10天加
工完成,则甲组需要加工多少天?
解:(1)设甲组平均每天能加
工x袋粽子,乙组平均每天能加
工y袋粽子,
(2)设甲组需要加工m天,则乙组加工(10-m)天,
答:甲组平均每天能加工200袋粽子,乙组平均每天能加工150袋粽子.
由题意得:
解得:
由题意得:200m+150(10-m)=1700,
解得:m=4,
答:甲组需要加工4天.
谢谢您的聆听!
二元一次方程组(复习)
知识脉络
二
元
一
次
方
程
组
概念
二元一次方程
二元一次方程的解
二元一次方程组
二元一次方程组的解
解法
代入消元法
加减消元法
思路
消元
二元
一元
应用
利用二元一次方程
组解决实际问题
知识回顾
1.概念
(1)什么是二元一次方程?什么是二元一次方程的解?
答:含有两个未知数,并且所含未知数的项的次数都是
1的方程叫做二元一次方程,能使二元一次方程左右两边
相等的一对值叫做二元一次方程的一个解.
(2)什么是二元一次方程组?什么是二元一次方程组的解?
答:含有两个未知数的两个一次方程组成的方程组叫做二
元一次方程组.二元一次方程组中两个方程的公共解叫做二
元一次方程组的解.
小试牛刀
下列方程中是二元一次方程的是( )
A.x=2y B.x+2y=z C.xy+1=0 D.
2.下列方程组属于二元一次方程组的是( )
A. B.
C. D.
A
D
3.若方程xm+2+4y3n-2=4是关于x,y的二元一次方程,
则(2m+n)2023= .
4.若 是方程ax+by=3的解,则2a+4b+5= .
5. 若方程组 的解为 , 则a+b的
值为 .
m+2=1
3n-2=1
解得
m=-1
n=1
2m+n=-1
代入
(2m+n)2023 =-1
-1
a+2b=3
代入
2a+4b=6
×2
2a+4b+5=11
+5
11
代入
解得
a+b =2-1=1
代入
1
知识回顾
2.解法
解二元一次方程组的基本思想是什么?
二元一次方程组
一元一次方程
消元
化归
怎样解二元一次方程组呢?
代入消元法和加减消元法
典例精解
例1 解方程组:
(1) (2)
解:把①代入②,得x+x+1=5
解得x=2
把x=2代入①,得y=3
所以方程组的解为
解:①+②,得4x=8
解得x=2
把x=2代入①,得2+2y=9
解得y=
所以方程组的解为
典例精解
例2 解方程组:
(1) (2)
解:由②,得3x+2y=15③,
由①,得y=5-4x,
把y=5-4x代入③,
得3x+2(5-4x)=15
解得x=-1,
把x=-1代入y=5-4x,得y=9
所以方程组的解为
解:由①,得2x-3y=9 ③ ,
由②,得2x-y=3④,
③-④ ,得-2y=6,即y=-3,
把y=-3代入④ ,得2x-(-3)=3,
解得x=0,
所以方程组的解为
典例精解
例3 解方程组:
解:由②-①,得3(x-y)=6 ,解得x-y=2③,
得新方程组
解得:
所以方程组的解为
把x-y=2代入①,得x+y= ④,
小试牛刀
6.解方程组:
(1) (2)
(3) (4)
请按暂停,用5~10分钟时间解完上述题目,再继续.
小试牛刀
6.解方程组:
(1) (2)
(3) (4)
你解对了吗?如果解错了,请找一找错在哪里.
知识回顾
3.三元一次方程组的解法
三元一次方程组
一元一次方程
消元
化归
二元一次方程组
消元
化归
典例精解
例4 解方程组:
解:由①-②,得-2b=4,解得b=-2 ,
把b=-2分别代入① ,③得
解得a=1,c=-3
所以方程组的解为
知识回顾
4.二元一次方程组的应用
典例精解
例5 端午临仲夏,时清日复长.“临近端午节,一网红门店接
到一份粽子订单,立即决定由甲、乙两组加工完成.已知甲、
乙两组加工一天共生产350袋粽子,甲组加工2天比乙组加工1
天多生产250袋粽子.
(1)求甲、乙两组平均每天各能加工多少袋粽子?
(2)已知这份粽子订单为1700袋,若甲、乙两组共用10天加
工完成,则甲组需要加工多少天?
解:(1)设甲组平均每天能加
工x袋粽子,乙组平均每天能加
工y袋粽子,
(2)设甲组需要加工m天,则乙组加工(10-m)天,
答:甲组平均每天能加工200袋粽子,乙组平均每天能加工150袋粽子.
由题意得:
解得:
由题意得:200m+150(10-m)=1700,
解得:m=4,
答:甲组需要加工4天.
谢谢您的聆听!
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
