初中数学浙教版七年级下册第一章 平行线小结课件（20张PPT）

(共20张PPT)
第一章 平行线复习
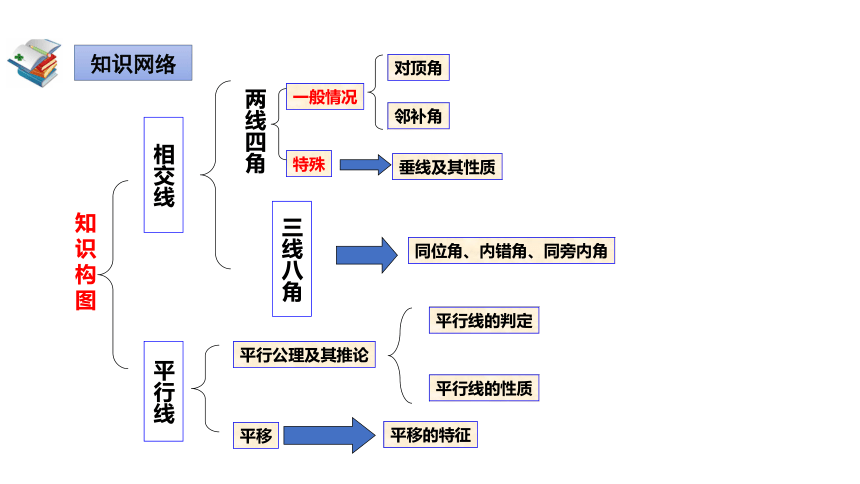
知识网络
相交线
一般情况
对顶角
邻补角
特殊
垂线及其性质
同位角、内错角、同旁内角
平行线
平行公理及其推论
平行线的判定
平行线的性质
平移
平移的特征
知识构图
两线四角
三线八角
知识点1 平行线
知识梳理
①在同一平面内
1.定义：在同一平面内不相交的两条直线叫做平行线.
②不相交
a
b
表示：
a∥b
读作：a平行于b 　
D
B
A
C
·
·
·
·
或AB∥CD
同一平面内，不重合的两条直线有两种位置关系：
相交或平行
·
A
B
C
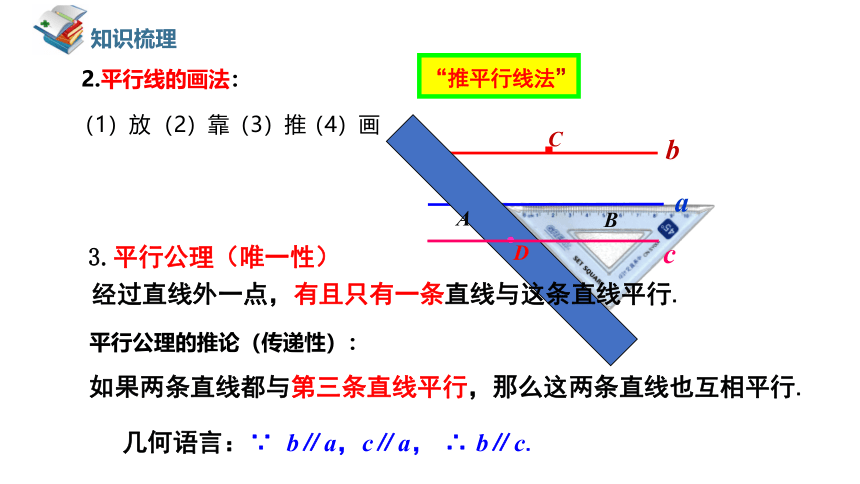
经过直线外一点，有且只有一条直线与这条直线平行.
b
a
·
D
3.平行公理（唯一性）
c
平行公理的推论（传递性）：
如果两条直线都与第三条直线平行，那么这两条直线也互相平行.
几何语言：∵ b∥a，c∥a， ∴ b∥c.
（1）放
（2）靠
（3）推
（4）画
“推平行线法”
2.平行线的画法：
知识梳理
同位角、内错角、同旁内角的结构特征:
同位角 “F”型
内错角 “Z”型
同旁内角 “U”型
三线八角
知识点2 同位角、内错角与同旁内角
知识梳理
4.平行线的判定定理
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定
知识点3 平行线的判定与性质
知识梳理
1.平行线的定义：在同一平面内不相交的两条直线叫做平行线.
2.平行公理：经过直线外一点，有且只有一条直线与这条直线平行.
3.如果两条直线都平行于第三条直线，那么这两条直线平行（平行线的传递性）.
平行线的性质定理
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定
平行线的性质
知识点3 平行线的判定与性质
知识梳理
∵　∠3＝∠2
∴　AB∥CD（同位角相等，两直线平行）
文字
图形
符号
∵　∠1＝∠2
∴　AB∥CD（内错角相等，两直线平行）
几何符号语言：
∵AB∥CD
∴∠3=∠2（两直线平行，同位角相等））
∵ AB∥CD
∴∠1＝∠2（两直线平行，内错角相等）
∵　∠4＋∠2＝180°
∴　AB∥CD（同旁内角互补，两直线平行）
∵AB∥CD1
∴∠4＋∠2＝180°（两直线平行，同旁内角互补）
巩固练习
1.如图，下列条件中：①∠B+∠BCD＝180°；②∠1＝∠2；③∠3＝∠4；④∠B＝∠5．能判定AB∥CD的条件有 　 　．
①
2.一副三角板摆放如图所示，斜边FD 与直角边AC 相交于点E，点D在直角边BC上，且FD∥AB，∠B＝30°，则∠ADB 的度数是（　　）
A．95° B．105° C．115° D．125°
B
③
④
A
B
C
E
F
D
知识点4 图形的平移
知识梳理
1.平移的概念：一个图形沿某个方向移动，在移动的过程中，原图形上所有的点都沿同一个方向移动相等的距离，这样的图形运动叫做图形的平移.
2.平移的性质：
(1)平移不改变图形的形状和大小;
(2)一个图形和它经过平移所得的图形中，两组对应点的连线平行(或在同一条直线上)且相等.
3.如图，在Rt△ABC中，∠C＝90°，∠A＝33°，将△ABC 沿AB方向向右平移得到△DEF．（温馨提示：三角形三个内角的和等于180°）
（1）试求出∠E 的度数；
（2）若AE＝9cm，DB＝2cm．请求出CF 的长度．
解：
（1）∵在Rt△ABC中，∠C＝90°，∠A＝33°，
∴∠CBA＝180°- 90°﹣33°＝57°，
由平移性质得，∠E＝∠CBA＝57°；
（2）由平移性质得，AD＝BE＝CF，
∵AE＝9cm，DB＝2cm，
∴CF＝3.5cm．
巩固练习
∴AD＝BE＝1/2×（9﹣2）＝3.5cm，
4.如图，将一条对边互相平行的纸带进行两次折叠，折痕分别为 , .
若 ， ，则∠2的度数为 ( )
C
A. B. C. D.
F
G
3
4
5
6
巩固练习
问题情境：“公路村村通”的政策让公路修到了山里，蜿蜒的盘山公路连接了山里与山外的世界.数学活动课上，老师把山路抽象成图1所示的样子，并提出了一个问题：
（1） ， ， ，求 的度数.
综合应用
图1
分析
从条件看：
1.有平行线，但没有截线；
2.有角，但不构成等角的同位角、内错角.
探究：需要添加辅助线转化条件，让平行线的性质
或判定发挥作用.
（1） ， ， ，求 的度数.
综合应用
图1
∵∠B＝125°, ∴∠BPQ=55°.
∵PQ//CD, ∠C＝25°，∴∠CPQ＝∠C＝25°.
∴∠BPC＝∠BPQ+∠CPQ=55°+25°＝80°.
小康同学的解法：
解：如图1，过点P作PQ//AB，
∵AB//CD，
∴PQ//CD(平行于同一条直线的两条直线互相平行)
∵AB//PQ，
∴∠B+∠BPQ=180°(两直线平行,同旁内角互补).
（1） ， ， ，求 的度数.
综合应用
Q
R
图1
， ， ，求 的度数.请问同学们本题还有其他的解题方法吗？
E
(2)解：延长BP交CD于点E,
∴∠BPC＝180°-∠CPE=180°-100°＝80°.
∵AB//CD,
∴∠B+∠BEC=180°.
∵ ∠B＝125°, ∴∠BEC＝55°.
∵∠C＝25°, ∴∠CPE＝180°-55°-25°＝100°.
∵∠BPC+∠CPE=180°,
图1
综合应用
在解决平行线间的拐角问题时，当无法直接得到角的关系时，通常借助辅助线来帮助解答，如何作辅助线需根据已知条件确定，辅助线的添加既可以产生新的条件，又能将题目中原有的条件联系在一起.
E
F
R
（2）过“拐点”加截线(连接两点或延长线段)
（1）过“拐点”作平行线
常见辅助线的作法：
Q
G
H
添平行线
添截线
（3）聪明的小明在图1的基础上，将图1改变为图2，其中 ，
， ， ，求 的度数.
M
N
(3)解：过点P 作PN//AB，过点Q作QM//AB，
∠4＝180°-∠C=180°-145°＝35°.
∵AB//CD， ∴AB//PN//QM//CD.
∴∠B+∠1=180°,∠2=∠3,
∠4+∠C=180°.
∵ ∠B＝125°, ∠C＝145°,
∴∠1＝180°-∠B=180°-125°＝55°.
∴∠BPQ=∠1+∠2 =55°+30°＝85°.
∴∠2＝∠3＝30°.
∴∠3＝∠PQC-∠4=65°-35°＝30°.
∵ ∠PQC＝65°，
图1 图2
1
2
3
4
3.已知 AM∥CN，点B在直线AM、CN之间，∠ABC=88°．
(1)如图1，请直接写出∠A和∠C之间的数量关系：____________．
(2)如图2，∠A和∠C满足怎样的数量关系？请说明理由．
(3)如图3，AE平分∠MAB，CH平分∠NCB，AE与CH交于点G，求∠AGH的度数．
2.有一条长方形纸带，按如图所示沿AB折叠时，当∠1=30°，时求纸带重叠部分中∠CAB的度数为_________．
A
B
C
1
2
3
E
F
1.如图，在三角形 中，点 ， ， 分别在 ， ， 上， ， ，则下列结论错误的是( )
A. B.
C. D.
D
75°
∠A+∠C ＝88°
配套练习，助力提升
添平行线
添截线
画平行线、截线， 连结，延长等
平行线的问题
补全三线八角模型
补上第三 条平行线
课堂小结
1.解决平行线问题的常用方法是什么？
2.添加辅助线的常用方法是什么？具体如何操作？
常用方法
具体操作
同学们，再见