浙教版初中数学七年级下册第六单元《数据与统计图表 》单元测试卷(较易)(含详细答案解析)
文档属性
| 名称 | 浙教版初中数学七年级下册第六单元《数据与统计图表 》单元测试卷(较易)(含详细答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 698.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-11 12:48:06 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
浙教版初中数学七年级下册第六单元《数据与统计图表》单元测试卷
考试范围:第六章;考试时间:120分钟;总分:120分
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
1.为了考察库存只灯泡的使用寿命,从中任意抽取只灯泡进行实验,在这个问题中.下列说法正确的是( )
A. 总体是只灯泡 B. 样本是抽取的只灯泡
C. 个体是每只灯泡的使用寿命 D. 个体是只灯泡的使用寿命
2.要调查安顺市中学生了解禁毒知识的情况,下列抽样调查最适合的是( )
A. 在某中学抽取名女生 B. 在安顺市中学生中抽取名学生
C. 在某中学抽取名学生 D. 在安顺市中学生中抽取名男生
3.某校举办了一次“交通安全知识”测试,王老师从全校学生的答卷中随机抽取了名学生的答卷,并将测试成绩分为,,,四个等级,绘制出如图所示的条形统计图若该校学生共有名,则估计该校成绩为的学生人数为( )
A. B. C. D.
4.某校举办了一次“交通安全知识”测试,王老师从全校学生的答卷中随机抽取了名学生的答卷,并将测试成绩分为,,,四个等级,绘制出如图所示的条形统计图.若该校学生共有名,则估计该校成绩为的学生人数为
( )
A. B. C. D.
5.如图是一个还没画完整的扇形统计图,整个圆表示某班参加体育活动的总人数,其中参加立定跳远的人数占总人数的,则图中表示立定跳远人数的扇形是( )
A. B. C. D. .
6.下图所示的两个统计图中,女生人数多的学校是( )
A. 甲校 B. 乙校
C. 甲、乙两校女生人数一样多 D. 无法确定
7.如图是年中国新能源汽车购买用户地区分布图,由图可知下列说法错误的是( )
A. 一线城市购买新能源汽车的用户最多
B. 二线城市购买新能源汽车用户达
C. 三四线城市购买新能源汽车用户达到万
D. 四线城市以下购买新能源汽车用户最少
8.已知一个样本如下:,,,,,,,,,,对这些数据进行分组,其中这一组的频数是( )
A. B. C. D.
9.已知一组数据有个,把它分成组,第一组到第四组的频数分别是,,,,第组的频率为,则第组的频率是( )
A. B. C. D.
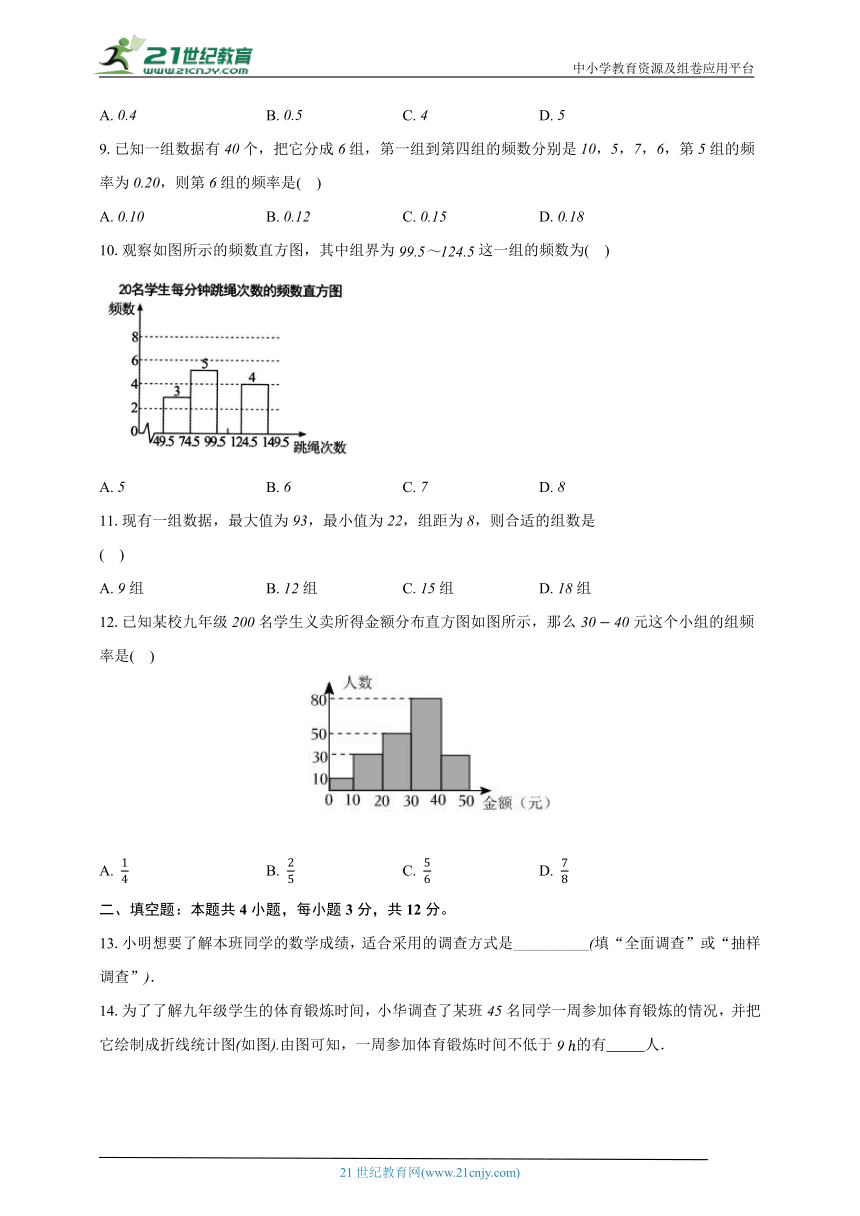
10.观察如图所示的频数直方图,其中组界为这一组的频数为( )
A. B. C. D.
11.现有一组数据,最大值为,最小值为,组距为,则合适的组数是
( )
A. 组 B. 组 C. 组 D. 组
12.已知某校九年级名学生义卖所得金额分布直方图如图所示,那么元这个小组的组频率是( )
A. B. C. D.
二、填空题:本题共4小题,每小题3分,共12分。
13.小明想要了解本班同学的数学成绩,适合采用的调查方式是__________填“全面调查”或“抽样调查”.
14.为了了解九年级学生的体育锻炼时间,小华调查了某班名同学一周参加体育锻炼的情况,并把它绘制成折线统计图如图由图可知,一周参加体育锻炼时间不低于的有 人.
15.如图,用整个圆表示某班同学参加四个兴趣小组的总人数,如果扇形代表人,那么扇形代表__________人.
16.赵老师想了解本校“生活中的数学知识”大赛的成绩分布情况,随机抽取了份试卷的成绩满分为分,成绩为整数,绘制成如图所示的统计图.由图可知,成绩不低于分的共有 人.
三、解答题:本题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
为了了解学生对学校伙食的满意程度,小红访问了名女生;小聪访问了名男生;小明访问了名男生和名女生,其中七年级、八年级和九年级各个年级的男生和女生各名.你认为小红、小聪、小明三人的抽样方法哪一种比较好?为什么?
18.本小题分
一厂家在某市三个经销该厂产品的商场进行调查,发现该厂产品的销售量占这三个商场同类产品销售量的,于是该厂声称,他们的产品占国内同类产品销售量的你认为这个说法可信吗?为什么?
19.本小题分
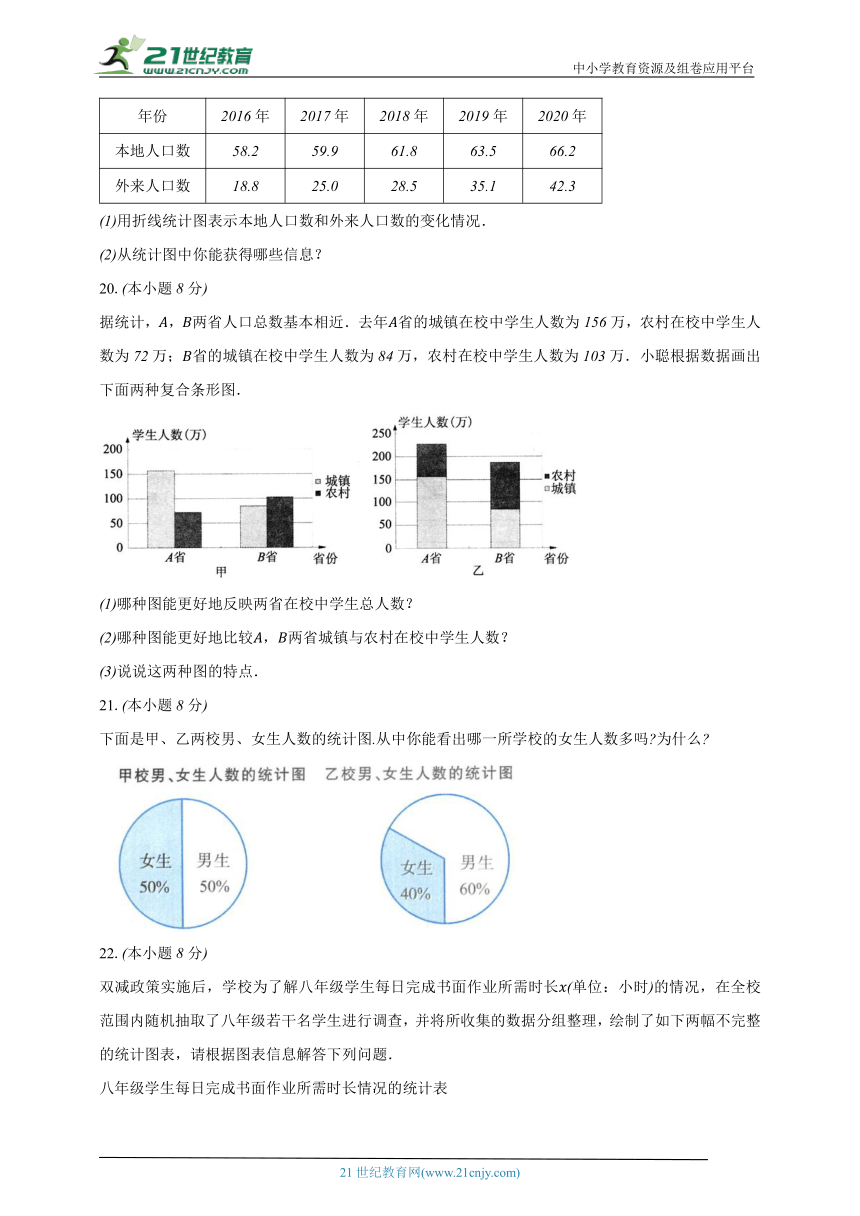
下面是年某市本地人口数和外来人口数统计表单位:万人.
年份 年 年 年 年 年
本地人口数
外来人口数
用折线统计图表示本地人口数和外来人口数的变化情况.
从统计图中你能获得哪些信息?
20.本小题分
据统计,,两省人口总数基本相近.去年省的城镇在校中学生人数为万,农村在校中学生人数为万;省的城镇在校中学生人数为万,农村在校中学生人数为万.小聪根据数据画出下面两种复合条形图.
哪种图能更好地反映两省在校中学生总人数?
哪种图能更好地比较,两省城镇与农村在校中学生人数?
说说这两种图的特点.
21.本小题分
下面是甲、乙两校男、女生人数的统计图从中你能看出哪一所学校的女生人数多吗为什么
22.本小题分
双减政策实施后,学校为了解八年级学生每日完成书面作业所需时长单位:小时的情况,在全校范围内随机抽取了八年级若干名学生进行调查,并将所收集的数据分组整理,绘制了如下两幅不完整的统计图表,请根据图表信息解答下列问题.
八年级学生每日完成书面作业所需时长情况的统计表
组别 所需时长小时 学生人数人
求统计表中,的值.
已知该校八年级学生有人,试估计该校八年级学生中每日完成书面作业所需时长满足的共有多少人.
23.本小题分
在某项针对岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为,规定:当时为级,当时为级,当时为级.现随机抽取个符合年龄条件的青年人开展每人“日均发微博条数”的调查,所抽青年人的“日均发微博条数”的数据如下:
求样本数据中为级的频率.
试估计个岁的青年人中“日均发微博条数”为级的人数.
24.本小题分
小李调查了两个班名男生最喜欢的足球运动员,结果如下分别代表四位足球运动员
,,,,,,,,,,,,,,,,,
,,,,,,,,,,,,,,,,,
,,,,,,,,,,,,,,,.
根据上述信息完成下面的频数表谁是这名男生最喜欢的足球运动员
名男生最喜欢的足球运动员的频数表
组别 划记 频数
25.本小题分
小明调查了七年级某班学生的身高后,制作了如下频数表未完成
七年级某班学生身高的频数表
组别 划记 频数
正
正正正
正
完成上面的频数表.
数据分组时的组距是多少
该班共有多少名学生身高在哪一个组的人数最多身高在哪一个组的人数最少
答案和解析
1.【答案】
【解析】解:、这只灯泡的使用寿命是总体,故本选项不合题意;
B、抽取的个灯泡的使用寿命是样本,故本选项不合题意;
C、每个灯泡的使用寿命是个体,故本选项符合题意;
D、个体是每只灯泡的使用寿命,故本选项不合题意.
故选:.
总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象.从而找出总体、个体.再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量.
本题考查了总体、个体、样本、样本容量的定义,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.
2.【答案】
【解析】解:、在某中学抽取名女生,抽样具有局限性,不合题意;
B、在安顺市中学生中抽取名学生,具有代表性,符合题意;
C、在某中学抽取名学生,抽样具有局限性,不合题意;
D、在安顺市中学生中抽取名男生,抽样具有局限性,不合题意;
故选:.
直接利用抽样调查中抽取的样本是否具有代表性,进而分析得出答案.
此题主要考查了抽样调查的意义,正确理解抽样调查是解题关键.
3.【答案】
【解析】略
4.【答案】
【解析】解:人,
即该校成绩为的学生人数估计为人,
故选:.
根据题目中的数据和统计图中的数据,可以计算出该校成绩为的学生人数.
本题考查条形统计图、用样本估计总体,解答本题的关键是明确题意,利用数形结合的思想解答.
5.【答案】
【解析】【分析】
本题考查对于扇形统计图的应用,属于容易题在扇形统计图中,每部分占总部分的百分比等于该部分所对应的扇形圆心角的度数与的比.
先求出的圆心角,再观察图形,即可作出选择.
【解答】
解:因为,再观察题干图形,只有所表示的扇形是钝角为直角,、为锐角.
6.【答案】
【解析】解答:
解:根据题意,因不知道甲乙两校学生的总人数,只知道两校女生占的比例,
故无法比较两校女生的人数,
故选:.
分析:根据题意,结合扇形图的性质,扇形统计图只能得到每部分所占的比例,具体人数不能直接体现,易得答案.
本题考查对扇形图意义的理解,即表现各部分占总体的百分比大小,直观表示各部分占总体的大小.
7.【答案】
【解析】解:、一线城市购买新能源汽车的用户最多,故本选项正确,不符合题意;
B、二线城市购买新能源汽车用户达,故本选项正确,不符合题意;
C、由扇形统计图中的数据不能得出三四线城市购买新能源汽车用户达到万,故本选项错误,符合题意;
D、四线城市以下购买新能源汽车用户最少,故本选项正确,不符合题意;
故选:.
根据扇形统计图中的数据一一分析即可判断.
本题考查了扇形统计图.关键是根据扇形统计图中的数据进行分析,解题时要细心.
8.【答案】
【解析】【分析】
此题考查了频数,掌握频数的定义是关键,根据频数的定义即可得到答案.
【解答】
解:在,,,,,,,,,中,
这一组的数有,,,,共个,
这一组的频数是,
故选C.
9.【答案】
【解析】解:根据第组的频率是,其频数是;
则第组的频数是.
故第组的频率是.
故选:.
先根据频率频数总数,以及第五组的频率是,可以求得第组的频数;再根据各组的频数和等于数据总数,求得第组的频数,从而求得其频率.
本题考查了频数和频率的知识,解答本题的关键是掌握频率频数数据总数以及各小组频数之和等于数据总数.
10.【答案】
【解析】【分析】
本题考查频数分布直方图,利用数形结合的思想解答是解答本题的关键.根据直方图中的数据,可以得到组界为这一组的频数.
【解答】
解:由直方图可得,组界为这一组的频数是.
11.【答案】
【解析】提示:根据组数计算,小数部分要进位在样本数据中最大值为,最小值为,它们的差是,组距为,那么,故组数为较合适.
12.【答案】
【解析】解:元这个小组的组频率是.
故选:.
根据“频率频数总数”即可得.
本题主要考查频数分布直方图,解题的关键是掌握频率频数总数.
13.【答案】全面调查
【解析】【分析】
本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似解答.
【解答】
解:了解某班同学数学成绩,人数不多,适合采用全面调查,
故答案为全面调查.
14.【答案】
【解析】略
15.【答案】
【解析】【分析】
此题主要考查了扇形统计图的应用,利用扇形的人数和圆心角得出总人数是解题关键.首先利用扇形代表人,扇形统计图中占,求出总人数,再利用扇形所对的圆心角度数即可求出扇形代表的人数.
【解答】
解:扇形代表人,扇形统计图中占,
扇形占比:,
总人数为:人,
扇形代表的人数是:人.
16.【答案】
【解析】略
17.【答案】解:小红访问了名女生,具有片面性,不合理;
小聪访问了名男生,具有片面性,不合理;
小明访问了名男生和名女生,其中七年级、八年级和九年级各个年级的男生和女生各名.具有代表性,合理;
故小明的抽样方法比较好.
【解析】抽样调查中,抽取的样本不能太片面,一定要具有代表性.
本题考查了抽样调查的性质:全面性;代表性.
18.【答案】解:因为调查只是在某市三个经销该厂产品的商场进行调查,不具有广泛性,因此不可信;理由:因为抽样不具有广泛性.
【解析】由于选择的样本在一个城市,太片面,所以不具有广泛性.数据不可靠.
本题考查了调查的对象的选择,要读懂题意,分清调查的内容所对应的调查对象是什么是解题的关键.注意所选取的对象要具有广泛性.
19.【答案】解:
答:外来人口增长较快答案不唯一
【解析】本题考查统计表、统计图.
根据统计表绘制折线统计图;以折线的上升或下降来表示统计数量的增减变化的统计图,叫作折线统计图折线统计图用折线的起伏表示数据的增减变化情况,不仅可以表示数量的多少,而且可以反映数据的增减变化情况;
仔细观察统计图,将从中得到的信息写出,该题为开放性试题,言之有理、符合题意即可.
20.【答案】解:图乙更好反映两省在校中学生总数;
图甲更好地比较省城镇和农村在校中学生人数;
图甲更直观地反映本省城镇与农村在校中学生人数的差别;
图乙更好反映两省在校中学生总数的差别.
【解析】本题考查读条形统计图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
根据两个图直接可以写出答案;
根据、比较的结果写出即可.
21.【答案】不能,因为不知道两个学校各自总人数
【解析】略
22.【答案】解:被调查总人数:人,
人,
人,
答:为,为;
当时,在被调查的人中有人,
在该校八年级学生人中,每日完成书面作业所需时长满足的共有人,
答:估计共有人.
【解析】先求出被调查总人数,再根据扇形统计图求出,用总人数减去、、的人数,即可得的值;
用被调查情况估计八年级人的情况,即可得到答案.
本题考查统计图和统计表,解题的关键是掌握从图表中寻找“完整信息”从而求出被调查的总数.
23.【答案】【小题】
的有人,则频率.
【小题】
人,即个岁的青年人中“日均发微博条数”为级的人数约为.
【解析】 略
略
24.【答案】略
【解析】略
25.【答案】【小题】略
【小题】
【小题】人身高在的最多,身高在的最少
【解析】 略
略
略
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
浙教版初中数学七年级下册第六单元《数据与统计图表》单元测试卷
考试范围:第六章;考试时间:120分钟;总分:120分
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
1.为了考察库存只灯泡的使用寿命,从中任意抽取只灯泡进行实验,在这个问题中.下列说法正确的是( )
A. 总体是只灯泡 B. 样本是抽取的只灯泡
C. 个体是每只灯泡的使用寿命 D. 个体是只灯泡的使用寿命
2.要调查安顺市中学生了解禁毒知识的情况,下列抽样调查最适合的是( )
A. 在某中学抽取名女生 B. 在安顺市中学生中抽取名学生
C. 在某中学抽取名学生 D. 在安顺市中学生中抽取名男生
3.某校举办了一次“交通安全知识”测试,王老师从全校学生的答卷中随机抽取了名学生的答卷,并将测试成绩分为,,,四个等级,绘制出如图所示的条形统计图若该校学生共有名,则估计该校成绩为的学生人数为( )
A. B. C. D.
4.某校举办了一次“交通安全知识”测试,王老师从全校学生的答卷中随机抽取了名学生的答卷,并将测试成绩分为,,,四个等级,绘制出如图所示的条形统计图.若该校学生共有名,则估计该校成绩为的学生人数为
( )
A. B. C. D.
5.如图是一个还没画完整的扇形统计图,整个圆表示某班参加体育活动的总人数,其中参加立定跳远的人数占总人数的,则图中表示立定跳远人数的扇形是( )
A. B. C. D. .
6.下图所示的两个统计图中,女生人数多的学校是( )
A. 甲校 B. 乙校
C. 甲、乙两校女生人数一样多 D. 无法确定
7.如图是年中国新能源汽车购买用户地区分布图,由图可知下列说法错误的是( )
A. 一线城市购买新能源汽车的用户最多
B. 二线城市购买新能源汽车用户达
C. 三四线城市购买新能源汽车用户达到万
D. 四线城市以下购买新能源汽车用户最少
8.已知一个样本如下:,,,,,,,,,,对这些数据进行分组,其中这一组的频数是( )
A. B. C. D.
9.已知一组数据有个,把它分成组,第一组到第四组的频数分别是,,,,第组的频率为,则第组的频率是( )
A. B. C. D.
10.观察如图所示的频数直方图,其中组界为这一组的频数为( )
A. B. C. D.
11.现有一组数据,最大值为,最小值为,组距为,则合适的组数是
( )
A. 组 B. 组 C. 组 D. 组
12.已知某校九年级名学生义卖所得金额分布直方图如图所示,那么元这个小组的组频率是( )
A. B. C. D.
二、填空题:本题共4小题,每小题3分,共12分。
13.小明想要了解本班同学的数学成绩,适合采用的调查方式是__________填“全面调查”或“抽样调查”.
14.为了了解九年级学生的体育锻炼时间,小华调查了某班名同学一周参加体育锻炼的情况,并把它绘制成折线统计图如图由图可知,一周参加体育锻炼时间不低于的有 人.
15.如图,用整个圆表示某班同学参加四个兴趣小组的总人数,如果扇形代表人,那么扇形代表__________人.
16.赵老师想了解本校“生活中的数学知识”大赛的成绩分布情况,随机抽取了份试卷的成绩满分为分,成绩为整数,绘制成如图所示的统计图.由图可知,成绩不低于分的共有 人.
三、解答题:本题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
为了了解学生对学校伙食的满意程度,小红访问了名女生;小聪访问了名男生;小明访问了名男生和名女生,其中七年级、八年级和九年级各个年级的男生和女生各名.你认为小红、小聪、小明三人的抽样方法哪一种比较好?为什么?
18.本小题分
一厂家在某市三个经销该厂产品的商场进行调查,发现该厂产品的销售量占这三个商场同类产品销售量的,于是该厂声称,他们的产品占国内同类产品销售量的你认为这个说法可信吗?为什么?
19.本小题分
下面是年某市本地人口数和外来人口数统计表单位:万人.
年份 年 年 年 年 年
本地人口数
外来人口数
用折线统计图表示本地人口数和外来人口数的变化情况.
从统计图中你能获得哪些信息?
20.本小题分
据统计,,两省人口总数基本相近.去年省的城镇在校中学生人数为万,农村在校中学生人数为万;省的城镇在校中学生人数为万,农村在校中学生人数为万.小聪根据数据画出下面两种复合条形图.
哪种图能更好地反映两省在校中学生总人数?
哪种图能更好地比较,两省城镇与农村在校中学生人数?
说说这两种图的特点.
21.本小题分
下面是甲、乙两校男、女生人数的统计图从中你能看出哪一所学校的女生人数多吗为什么
22.本小题分
双减政策实施后,学校为了解八年级学生每日完成书面作业所需时长单位:小时的情况,在全校范围内随机抽取了八年级若干名学生进行调查,并将所收集的数据分组整理,绘制了如下两幅不完整的统计图表,请根据图表信息解答下列问题.
八年级学生每日完成书面作业所需时长情况的统计表
组别 所需时长小时 学生人数人
求统计表中,的值.
已知该校八年级学生有人,试估计该校八年级学生中每日完成书面作业所需时长满足的共有多少人.
23.本小题分
在某项针对岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为,规定:当时为级,当时为级,当时为级.现随机抽取个符合年龄条件的青年人开展每人“日均发微博条数”的调查,所抽青年人的“日均发微博条数”的数据如下:
求样本数据中为级的频率.
试估计个岁的青年人中“日均发微博条数”为级的人数.
24.本小题分
小李调查了两个班名男生最喜欢的足球运动员,结果如下分别代表四位足球运动员
,,,,,,,,,,,,,,,,,
,,,,,,,,,,,,,,,,,
,,,,,,,,,,,,,,,.
根据上述信息完成下面的频数表谁是这名男生最喜欢的足球运动员
名男生最喜欢的足球运动员的频数表
组别 划记 频数
25.本小题分
小明调查了七年级某班学生的身高后,制作了如下频数表未完成
七年级某班学生身高的频数表
组别 划记 频数
正
正正正
正
完成上面的频数表.
数据分组时的组距是多少
该班共有多少名学生身高在哪一个组的人数最多身高在哪一个组的人数最少
答案和解析
1.【答案】
【解析】解:、这只灯泡的使用寿命是总体,故本选项不合题意;
B、抽取的个灯泡的使用寿命是样本,故本选项不合题意;
C、每个灯泡的使用寿命是个体,故本选项符合题意;
D、个体是每只灯泡的使用寿命,故本选项不合题意.
故选:.
总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象.从而找出总体、个体.再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量.
本题考查了总体、个体、样本、样本容量的定义,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.
2.【答案】
【解析】解:、在某中学抽取名女生,抽样具有局限性,不合题意;
B、在安顺市中学生中抽取名学生,具有代表性,符合题意;
C、在某中学抽取名学生,抽样具有局限性,不合题意;
D、在安顺市中学生中抽取名男生,抽样具有局限性,不合题意;
故选:.
直接利用抽样调查中抽取的样本是否具有代表性,进而分析得出答案.
此题主要考查了抽样调查的意义,正确理解抽样调查是解题关键.
3.【答案】
【解析】略
4.【答案】
【解析】解:人,
即该校成绩为的学生人数估计为人,
故选:.
根据题目中的数据和统计图中的数据,可以计算出该校成绩为的学生人数.
本题考查条形统计图、用样本估计总体,解答本题的关键是明确题意,利用数形结合的思想解答.
5.【答案】
【解析】【分析】
本题考查对于扇形统计图的应用,属于容易题在扇形统计图中,每部分占总部分的百分比等于该部分所对应的扇形圆心角的度数与的比.
先求出的圆心角,再观察图形,即可作出选择.
【解答】
解:因为,再观察题干图形,只有所表示的扇形是钝角为直角,、为锐角.
6.【答案】
【解析】解答:
解:根据题意,因不知道甲乙两校学生的总人数,只知道两校女生占的比例,
故无法比较两校女生的人数,
故选:.
分析:根据题意,结合扇形图的性质,扇形统计图只能得到每部分所占的比例,具体人数不能直接体现,易得答案.
本题考查对扇形图意义的理解,即表现各部分占总体的百分比大小,直观表示各部分占总体的大小.
7.【答案】
【解析】解:、一线城市购买新能源汽车的用户最多,故本选项正确,不符合题意;
B、二线城市购买新能源汽车用户达,故本选项正确,不符合题意;
C、由扇形统计图中的数据不能得出三四线城市购买新能源汽车用户达到万,故本选项错误,符合题意;
D、四线城市以下购买新能源汽车用户最少,故本选项正确,不符合题意;
故选:.
根据扇形统计图中的数据一一分析即可判断.
本题考查了扇形统计图.关键是根据扇形统计图中的数据进行分析,解题时要细心.
8.【答案】
【解析】【分析】
此题考查了频数,掌握频数的定义是关键,根据频数的定义即可得到答案.
【解答】
解:在,,,,,,,,,中,
这一组的数有,,,,共个,
这一组的频数是,
故选C.
9.【答案】
【解析】解:根据第组的频率是,其频数是;
则第组的频数是.
故第组的频率是.
故选:.
先根据频率频数总数,以及第五组的频率是,可以求得第组的频数;再根据各组的频数和等于数据总数,求得第组的频数,从而求得其频率.
本题考查了频数和频率的知识,解答本题的关键是掌握频率频数数据总数以及各小组频数之和等于数据总数.
10.【答案】
【解析】【分析】
本题考查频数分布直方图,利用数形结合的思想解答是解答本题的关键.根据直方图中的数据,可以得到组界为这一组的频数.
【解答】
解:由直方图可得,组界为这一组的频数是.
11.【答案】
【解析】提示:根据组数计算,小数部分要进位在样本数据中最大值为,最小值为,它们的差是,组距为,那么,故组数为较合适.
12.【答案】
【解析】解:元这个小组的组频率是.
故选:.
根据“频率频数总数”即可得.
本题主要考查频数分布直方图,解题的关键是掌握频率频数总数.
13.【答案】全面调查
【解析】【分析】
本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似解答.
【解答】
解:了解某班同学数学成绩,人数不多,适合采用全面调查,
故答案为全面调查.
14.【答案】
【解析】略
15.【答案】
【解析】【分析】
此题主要考查了扇形统计图的应用,利用扇形的人数和圆心角得出总人数是解题关键.首先利用扇形代表人,扇形统计图中占,求出总人数,再利用扇形所对的圆心角度数即可求出扇形代表的人数.
【解答】
解:扇形代表人,扇形统计图中占,
扇形占比:,
总人数为:人,
扇形代表的人数是:人.
16.【答案】
【解析】略
17.【答案】解:小红访问了名女生,具有片面性,不合理;
小聪访问了名男生,具有片面性,不合理;
小明访问了名男生和名女生,其中七年级、八年级和九年级各个年级的男生和女生各名.具有代表性,合理;
故小明的抽样方法比较好.
【解析】抽样调查中,抽取的样本不能太片面,一定要具有代表性.
本题考查了抽样调查的性质:全面性;代表性.
18.【答案】解:因为调查只是在某市三个经销该厂产品的商场进行调查,不具有广泛性,因此不可信;理由:因为抽样不具有广泛性.
【解析】由于选择的样本在一个城市,太片面,所以不具有广泛性.数据不可靠.
本题考查了调查的对象的选择,要读懂题意,分清调查的内容所对应的调查对象是什么是解题的关键.注意所选取的对象要具有广泛性.
19.【答案】解:
答:外来人口增长较快答案不唯一
【解析】本题考查统计表、统计图.
根据统计表绘制折线统计图;以折线的上升或下降来表示统计数量的增减变化的统计图,叫作折线统计图折线统计图用折线的起伏表示数据的增减变化情况,不仅可以表示数量的多少,而且可以反映数据的增减变化情况;
仔细观察统计图,将从中得到的信息写出,该题为开放性试题,言之有理、符合题意即可.
20.【答案】解:图乙更好反映两省在校中学生总数;
图甲更好地比较省城镇和农村在校中学生人数;
图甲更直观地反映本省城镇与农村在校中学生人数的差别;
图乙更好反映两省在校中学生总数的差别.
【解析】本题考查读条形统计图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
根据两个图直接可以写出答案;
根据、比较的结果写出即可.
21.【答案】不能,因为不知道两个学校各自总人数
【解析】略
22.【答案】解:被调查总人数:人,
人,
人,
答:为,为;
当时,在被调查的人中有人,
在该校八年级学生人中,每日完成书面作业所需时长满足的共有人,
答:估计共有人.
【解析】先求出被调查总人数,再根据扇形统计图求出,用总人数减去、、的人数,即可得的值;
用被调查情况估计八年级人的情况,即可得到答案.
本题考查统计图和统计表,解题的关键是掌握从图表中寻找“完整信息”从而求出被调查的总数.
23.【答案】【小题】
的有人,则频率.
【小题】
人,即个岁的青年人中“日均发微博条数”为级的人数约为.
【解析】 略
略
24.【答案】略
【解析】略
25.【答案】【小题】略
【小题】
【小题】人身高在的最多,身高在的最少
【解析】 略
略
略
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
