第5章 列分式方程解应用题精选中考真题50题(分层练习 综合练)(含解析)
文档属性
| 名称 | 第5章 列分式方程解应用题精选中考真题50题(分层练习 综合练)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-19 18:31:29 | ||
图片预览




文档简介
列分式方程解应用题精选中考真题50题(分层练习)(综合练)
一、单选题
1.(2023·四川内江·中考真题)用计算机处理数据,为了防止数据输入出错,某研究室安排两名程序操作员各输入一遍,比较两人的输入是否一致,本次操作需输入2640个数据,已知甲的输入速度是乙的2倍,结果甲比乙少用2小时输完.这两名操作员每分钟各能输入多少个数据?设乙每分钟能输入x个数据,根据题意得方程正确的是( )
A. B.
C. D.
2.(2023·湖北十堰·中考真题)为了落实“双减”政策,进一步丰富文体活动,学校准备购进一批篮球和足球,已知每个篮球的价格比每个足球的价格多20元,用1500元购进篮球的数量比用800元购进足球的数量多5个,如果设每个足球的价格为x元,那么可列方程为( )
A. B. C. D.
3.(2023·四川·中考真题)近年来,我市大力发展交通,建成多条快速通道,小张开车从家到单位有两条路线可选择,路线a为全程10千米的普通道路,路线b包含快速通道,全程7千米,走路线b比路线a平均速度提高,时间节省10分钟,求走路线a和路线b的平均速度分别是多少?设走路线a的平均速度为x千米/小时,依题意,可列方程为( )
A. B.
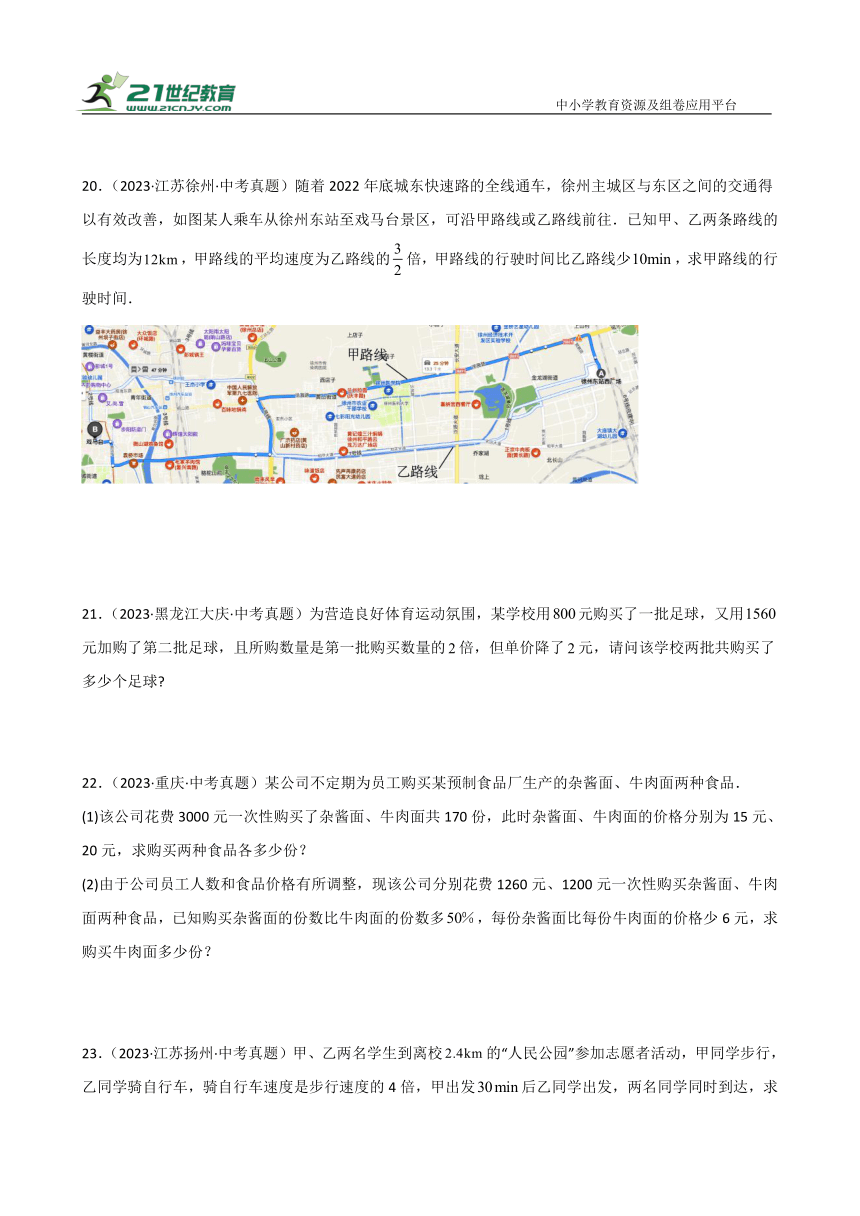
C. D.
4.(2023·广东深圳·中考真题)某运输公司运输一批货物,已知大货车比小货车每辆多运输5吨货物,且大货车运输75吨货物所用车辆数与小货车运输50吨货物所用车辆数相同,设有大货车每辆运输x吨,则所列方程正确的是( )
A. B. C. D.
5.(2023·黑龙江绥化·中考真题)某运输公司,运送一批货物,甲车每天运送货物总量的.在甲车运送1天货物后,公司增派乙车运送货物,两车又共同运送货物天,运完全部货物.求乙车单独运送这批货物需多少天?设乙车单独运送这批货物需x天,由题意列方程,正确的是( )
A. B.
C. D.
6.(2023·山东东营·中考真题)为扎实推进“五育”并举工作,加强劳动教育,东营市某中学针对七年级学生开设了“跟我学面点”烹饪课程,课程开设后学校花费6000元购进第一批面粉,用完后学校又花费9600元购进了第二批面粉,第二批面粉的采购量是第一批采购量的1.5倍,但每千克面粉价格提高了0.4元.设第一批面粉采购量为x千克,依题意所列方程正确的是( )
A. B.
C. D.
7.(2023·辽宁·中考真题)某校八年级学生去距离学校的游览区游览,一部分学生乘慢车先行,出发后,另一部分学生乘快车前往,结果他们同时到达.已知快车的速度是慢车速度的倍,求慢车的速度,设慢车的速度是,所列方程正确的是( )
A. B. C. D.
8.(2023·青海·中考真题)为了缅怀革命先烈,传承红色精神,青海省某学校八年级师生在清明节期间前往距离学校的烈士陵园扫墓.一部分师生骑自行车先走,过了后,其余师生乘汽车出发,结果他们同时到达;已知汽车的速度是骑车师生速度的2倍,设骑车师生的速度为.根据题意,下列方程正确的是( )
A. B. C. D.
9.(2023·四川达州·中考真题)某镇的“脆红李”深受广大市民的喜爱,也是馈赠亲友的尚佳礼品,首批“脆红李”成熟后,当地某电商用12000元购进这种“脆红李”进行销售,面市后,线上订单猛增供不应求,该电商又用11000元购进第二批这种“脆红李”,由于更多“脆红李”成熟,单价比第一批每件便宜了5元,但数量比第一批多购进了40件,求购进的第一批“脆红李”的单价.设购进的第一批“脆红李”的单价为x元/件,根据题意可列方程为( )
A. B.
C. D.
10.(2023·云南·中考真题)阅读,正如一束阳光.孩子们无论在哪儿,都可以感受到阳光的照耀,都可以通过阅读触及更广阔的世界.某区教育体育局向全区中小学生推出“童心读书会”的分享活动.甲、乙两同学分别从距离活动地点800米和400米的两地同时出发,参加分享活动.甲同学的速度是乙同学的速度的1.2倍,乙同学比甲同学提前4分钟到达活动地点.若设乙同学的速度是米/分,则下列方程正确的是( )
A. B. C. D.
11.(2023·湖北随州·中考真题)甲、乙两个工程队共同修一条道路,其中甲工程队需要修9千米,乙工程队需要修12千米.已知乙工程队每个月比甲工程队多修1千米,最终用的时间比甲工程队少半个月.若设甲工程队每个月修x千米,则可列出方程为( )
A. B. C. D.
12.(2023·广东广州·中考真题)随着城际交通的快速发展,某次动车平均提速60,动车提速后行驶480与提速前行驶360所用的时间相同.设动车提速后的平均速度为x,则下列方程正确的是( )
A. B. C. D.
二、解答题
13.(2023·贵州·中考真题)为推动乡村振兴,政府大力扶持小型企业.根据市场需求,某小型企业为加快生产速度,需要更新生产设备,更新设备后生产效率比更新前提高了,设更新设备前每天生产x件产品.解答下列问题:
(1)更新设备后每天生产_______件产品(用含x的式子表示);
(2)更新设备前生产5000件产品比更新设备后生产6000件产品多用2天,求更新设备后每天生产多少件产品.
14.(2023·四川乐山·中考真题)为了践行习近平总书记提出的“绿水青山就是金山银山”的发展理念,某地计划在规定时间内种植梨树棵.开始种植时,由于志愿者的加入,实际每天种植梨树的数量比原计划增加了,结果提前2天完成任务.问原计划每天种植梨树多少棵?
15.(2023·湖南岳阳·中考真题)水碧万物生,岳阳龙虾好.小龙虾产业已经成为岳阳乡村振兴的“闪亮名片”.已知翠翠家去年龙虾的总产量是,今年龙虾的总产量是,且去年与今年的养殖面积相同,平均亩产量去年比今年少,求今年龙虾的平均亩产量.
16.(2023·广东·中考真题)某学校开展了社会实践活动,活动地点距离学校,甲、乙两同学骑自行车同时从学校出发,甲的速度是乙的倍,结果甲比乙早到,求乙同学骑自行车的速度.
17.(2023·湖南常德·中考真题)“六一”儿童节将至,张老板计划购买A型玩具和B型玩具进行销售,若用1200元购买A型玩具的数量比用1500元购买B型玩具的数量多20个,且一个B型玩具的进价是一个A型玩具进价的1.5倍.
(1)求A型玩具和B型玩具的进价分别是多少?
(2)若A型玩具的售价为12元/个,B型玩具的售价为20元/个,张老板购进A,B型玩具共75个,要使总利润不低于300元,则A型玩具最多购进多少个?
18.(2023·吉林长春·中考真题)随着中国网民规模突破亿、博物馆美育不断向线上拓展.敦煌研究院顺势推出数字敦煌文化大使伽瑶,受到广大敦煌文化爱好者的好评.某工厂计划制作个伽瑶玩偶摆件,为了尽快完成任务,实际平均每天完成的数量是原计划的倍,结果提前天完成任务.问原计划平均每天制作多少个摆件?
19.(2023·辽宁沈阳·中考真题)甲、乙两人加工同一种零件,每小时甲比乙多加工个这种零件,甲加工个这种零件所用的时间与乙加工个这种零件所用的时间相等,求乙每小时加工多少个这种零件.
20.(2023·江苏徐州·中考真题)随着2022年底城东快速路的全线通车,徐州主城区与东区之间的交通得以有效改善,如图某人乘车从徐州东站至戏马台景区,可沿甲路线或乙路线前往.已知甲、乙两条路线的长度均为,甲路线的平均速度为乙路线的倍,甲路线的行驶时间比乙路线少,求甲路线的行驶时间.
21.(2023·黑龙江大庆·中考真题)为营造良好体育运动氛围,某学校用元购买了一批足球,又用元加购了第二批足球,且所购数量是第一批购买数量的倍,但单价降了元,请问该学校两批共购买了多少个足球
22.(2023·重庆·中考真题)某公司不定期为员工购买某预制食品厂生产的杂酱面、牛肉面两种食品.
(1)该公司花费3000元一次性购买了杂酱面、牛肉面共170份,此时杂酱面、牛肉面的价格分别为15元、20元,求购买两种食品各多少份?
(2)由于公司员工人数和食品价格有所调整,现该公司分别花费1260元、1200元一次性购买杂酱面、牛肉面两种食品,已知购买杂酱面的份数比牛肉面的份数多,每份杂酱面比每份牛肉面的价格少6元,求购买牛肉面多少份?
23.(2023·江苏扬州·中考真题)甲、乙两名学生到离校的“人民公园”参加志愿者活动,甲同学步行,乙同学骑自行车,骑自行车速度是步行速度的4倍,甲出发后乙同学出发,两名同学同时到达,求乙同学骑自行车的速度.
24.(2023·山东·中考真题)某校组织学生去郭永怀纪念馆进行研学活动.纪念馆距学校72千米,部分学生乘坐大型客车先行,出发12分钟后,另一部分学生乘坐小型客车前往,结果同时到达.已知小型客车的速度是大型客车速度的倍,求大型客车的速度.
25.(2023·山东泰安·中考真题)为进行某项数学综合与实践活动,小明到一个批发兼零售的商店购买所需工具.该商店规定一次性购买该工具达到一定数量后可以按批发价付款,否则按零售价付款.小明如果给学校九年级学生每人购买一个,只能按零售价付款,需用3600元;如果多购买60个,则可以按批发价付款,同样需用3600元,若按批发价购买60个与按零售价购买50个所付款相同,求这个学校九年级学生有多少人?
26.(2023·辽宁锦州·中考真题)2023年5月15日,辽宁男篮取得第三次CBA总冠军,辽篮运动员的拼搏精神感染了众多球迷.某校篮球社团人数迅增,急需购进A,B两种品牌篮球,已知A品牌篮球单价比B品牌篮球单价的2倍少48元,采购相同数量的A,B两种品牌篮球,分别需要花费9600元和7200元.求A,B两种品牌篮球的单价分别是多少元?
27.(2023·辽宁丹东·中考真题)“畅通交通,扮靓城市”,某市在道路提升改造中,将一座长度为36米的桥梁进行重新改造.为了尽快通车,某施工队在实际施工时,每天工作效率比原计划提高了,结果提前2天成功地完成了大桥的改造任务,那么该施工队原计划每天改造多少米
28.(2022·吉林长春·中考真题)为了让学生崇尚劳动,尊重劳动,在劳动中提升综合素质,某校定期开展劳动实践活动.甲、乙两班在一次体验挖土豆的活动中,甲班挖1500千克土豆与乙班挖1200千克土豆所用的时间相同.已知甲班平均每小时比乙班多挖100千克土豆,问乙班平均每小时挖多少千克土豆?
29.(2022·辽宁·中考真题)2022年3月23日“天宫课堂”第二课在中国空间站开讲了,精彩的直播激发了学生探索科学奥秘的兴趣.某中学为满足学生的需求,充实物理兴趣小组的实验项目,决定购入A、B两款物理实验套装,其中A款套装单价是B款套装单价的1.2倍,用9900元购买的A款套装数量比用7500元购买的B款套装数量多5套.求A、B两款套装的单价分别是多少元.
30.(2022·广西桂林·中考真题)今年,某市举办了一届主题为“强国复兴有我”的中小学课本剧比赛.某队伍为参赛需租用一批服装,经了解,在甲商店租用服装比在乙商店租用服装每套多10元,用500元在甲商店租用服装的数量与用400元在乙商店租用服装的数量相等.
(1)求在甲,乙两个商店租用的服装每套各多少元?
(2)若租用10套以上服装,甲商店给以每套九折优惠.该参赛队伍准备租用20套服装,请问在哪家商店租用服装的费用较少,并说明理由.
31.(2022·吉林·中考真题)刘芳和李婷进行跳绳比赛.已知刘芳每分钟比李婷多跳20个,刘芳跳135个所用的时间与李婷跳120个所用的时间相等.求李婷每分钟跳绳的个数.
32.(2022·黑龙江大庆·中考真题)某工厂生产某种零件,由于技术上的改进,现在平均每天比原计划多生产20个零件,现在生产800个零件所需时间与原计划生产600个零件所需时间相同.求现在平均每天生产多少个零件?
33.(2022·四川乐山·中考真题)第十四届四川省运动会定于2022年8月8日在乐山市举办,为保证省运会期间各场馆用电设施的正常运行,市供电局为此进行了电力抢修演练.现抽调区县电力维修工人到20千米远的市体育馆进行电力抢修.维修工人骑摩托车先行出发,10分钟后,抢修车装载完所需材料再出发,结果他们同时到达体育馆,已知抢修车是摩托车速度的1.5倍,求摩托车的速度.
34.(2022·江苏扬州·中考真题)某中学为准备十四岁青春仪式,原计划由八年级(1)班的4个小组制作360面彩旗,后因1个小组另有任务,其余3个小组的每名学生要比原计划多做3面彩旗才能完成任务.如果这4个小组的人数相等,那么每个小组有学生多少名?
35.(2022·重庆·中考真题)在全民健身运动中,骑行运动颇受市民青睐,甲、乙两骑行爱好者约定从地沿相同路线骑行去距地30千米的地,已知甲骑行的速度是乙的1.2倍.
(1)若乙先骑行2千米,甲才开始从地出发,则甲出发半小时恰好追上乙,求甲骑行的速度;
(2)若乙先骑行20分钟,甲才开始从地出发,则甲、乙恰好同时到达地,求甲骑行的速度.
36.(2022·重庆·中考真题)为保障蔬菜基地种植用水,需要修建灌溉水渠.
(1)计划修建灌溉水渠600米,甲施工队施工5天后,增加施工人员,每天比原来多修建20米,再施工2天完成任务,求甲施工队增加人员后每天修建灌溉水渠多少米?
(2)因基地面积扩大,现还需修建另一条灌溉水渠1800米,为早日完成任务,决定派乙施工队与甲施工队同时开工合作修建这条水渠,直至完工.甲施工队按(1)中增加人员后的修建速度进行施工.乙施工队修建360米后,通过技术更新,每天比原来多修建20%,灌溉水渠完工时,两施工队修建的长度恰好相同.求乙施工队原来每天修建灌溉水渠多少米?
37.(2022·四川自贡·中考真题)学校师生去距学校45千米的吴玉章故居开展研学活动,骑行爱好者张老师骑自行车先行2小时后,其余师生乘汽车出发,结果同时到达;已知汽车速度是自行车速度的3倍,求张老师骑车的速度.
38.(2022·山西·中考真题)2022年我国已成为全球最大的电动汽车市场,电动汽车在保障能源安全,改善空气质量等方面较传统汽车都有明显优势,经过对某款电动汽车和某款燃油车的对比调查发现,电动汽车平均每公里的充电费比燃油车平均每公里的加油费少0.6元.若充电费和加油费均为200元时,电动汽车可行驶的总路程是燃油车的4倍,求这款电动汽车平均每公里的充电费.
39.(2021·辽宁朝阳·中考真题)为了进一步丰富校园文体活动,学校准备购进一批篮球和足球,已知每个篮球的进价比每个足球的进价多25元,用2000元购进篮球的数量是用750元购进足球数量的2倍,求:每个篮球和足球的进价各多少元?
40.(2021·辽宁锦州·中考真题)小江与小杰两名同学为学校图书馆清点一批图书,小江清点完600本图书比小杰清点完540本图书少用了5min.已知小江平均每分钟清点图书的数量是小杰的1.25倍,求两名同学平均每分钟清点图书各多少本.
41.(2021·辽宁丹东·中考真题)为落实“乡村振兴计划”的工作要求,某区政府计划对乡镇道路进行改造,安排甲、乙两个工程队完成,已知乙队比甲队每天少改造20米,甲队改造400米的道路与乙队改造300米的道路所用时间相同,求甲、乙两个工程队每天改造的道路长度分别是多少米?
42.(2021·江苏徐州·中考真题)某网店开展促销活动,其商品一律按8折销售,促销期间用400元在该网店购得某商品的数量较打折前多出2件.问:该商品打折前每件多少元?
43.(2021·江苏常州·中考真题)为落实节约用水的政策,某旅游景点进行设施改造,将手拧水龙头全部更换成感应水龙头.已知该景点在设施改造后,平均每天用水量是原来的一半,20吨水可以比原来多用5天,该景点在设施改造后平均每天用水多少吨?
44.(2021·山东威海·中考真题)六一儿童节来临之际,某商店用3000元购进一批玩具,很快售完;第二次购进时,每件的进价提高了20%,同样用3000元购进的数量比第一次少了10件.
(1)求第一次每件的进价为多少元?
(2)若两次购进的玩具售价均为70元,且全部售完,求两次的总利润为多少元?
45.(2021·内蒙古·中考真题)小刚家到学校的距离是1800米.某天早上,小刚到学校后发现作业本忘在家中,此时离上课还有20分钟,于是他立即按原路跑步回家,拿到作业本后骑自行车按原路返回学校.已知小刚骑自行车时间比跑步时间少用了4.5分钟,且骑自行车的平均速度是跑步的平均速度的1.6倍.
(1)求小刚跑步的平均速度;
(2)如果小刚在家取作业本和取自行车共用了3分钟,他能否在上课前赶回学校?请说明理由.
46.(2021·湖南永州·中考真题)永州市某村经济合作社在乡村振兴工作队的指导下,根据市场需求,计划在2022年将30亩土地全部用于种植A,B两种经济作物.预计B种经济作物亩产值比A种经济作物亩产值多2万元,为实现2022年A种经济作物年总产值20万元,B种经济作物年总产值30万元的目标,问:2022年A,B两种经济作物应各种植多少亩?
47.(2021·吉林长春·中考真题)为助力乡村发展,某购物平台推出有机大米促销活动,其中每千克有机大米的售价仅比普通大米多2元,用420元购买的有机大米与用300元购买的普通大米的重量相同,求每千克有机大米的售价为多少元?
48.(2021·内蒙古通辽·中考真题)为做好新冠疫情的防控工作,某单位需购买甲、乙两种消毒液经了解每桶甲种消毒液的零售价比乙种消毒液的零售价多6元,该单位以零售价分别用900元和720元采购了相同桶数的甲、乙两种消毒液.
(1)求甲、乙两种消毒液的零售价分别是每桶多少元?
(2)由于疫情防控进入常态化,该单位需再次购买两种消毒液共300桶,且甲种消毒液的桶数不少于乙种消毒液桶数的,由于购买量大,甲、乙两种消毒液分别获得了20元/桶,15元/桶的批发价.求甲种消毒液购买多少桶时,所需资金总额最少?最少总金额是多少元?
49.(2021·江西·中考真题)甲,乙两人去市场采购相同价格的同一种商品,甲用2400元购买的商品数量比乙用3000元购买的商品数量少10件.
(1)求这种商品的单价;
(2)甲,乙两人第二次再去采购该商品时,单价比上次少了20元/件,甲购买商品的总价与上次相同,乙购买商品的数量与上次相同,则甲两次购买这种商品的平均单价是______元/件,乙两次购买这种商品的平均单价是______元/件.
(3)生活中,无论油价如何变化,有人总按相同金额加油,有人总按相同油量加油,结合(2)的计算结果,建议按相同______加油更合算(填“金额”或“油量”).
50.(2021·云南·中考真题)“30天无理由退货”是营造我省“诚信旅游”良好环境,进一步提升旅游形象的创新举措.机场、车站、出租车、景区、手机短信……,“30天无理由退货”的提示随处可见,它已成为一张云南旅行的“安心卡”,极大地提高了旅游服务的品质.刚刚过去的“五·一”假期,旅游线路、住宿、餐饮、生活服务、购物等旅游消费的供给更加多元,同步的是云南旅游市场强劲复苏.某旅行社今年5月1日租用A、B两种客房一天,供当天使用.下面是有关信息:今天用2000元租到A客房的数量与用1600元租到B客房的数量相等.今天每间A客房的租金比每间B客房的租金多40元.请根据上述信息,分别求今年5月1日该旅行社租用的A、B两种客房每间客房的租金.
中小学教育资源及组卷应用平台
试卷第1页,共3页
参考答案:
1.D
【分析】设乙每分钟能输入x个数据,则甲每分钟能输入个数据,根据“甲比乙少用2小时输完”列出分式方程即可.
【详解】解:设乙每分钟能输入x个数据,则甲每分钟能输入个数据,
由题意得,
故选:D.
【点拨】本题考查了由实际问题抽象出分式方程,找准等量关系,正确列出分式方程是解题的关键.
2.A
【分析】设每个足球的价格为x元,则篮球的价格为元,根据“用1500元购进篮球的数量比用800元购进足球的数量多5个”列方程即可.
【详解】解:设每个足球的价格为x元,则篮球的价格为元,
由题意可得:,
故选:A.
【点拨】本题考查分式方程的应用,正确理解题意是关键.
3.A
【分析】若设路线a时的平均速度为x千米/小时,则走路线b时的平均速度为千米/小时,根据路线b的全程比路线a少用10分钟可列出方程.
【详解】解:由题意可得走路线b时的平均速度为千米/小时,
∴,
故选:A.
【点拨】本题考查了由实际问题抽象出分式方程,找到关键描述语,找到合适的等量关系是解决问题的关键.
4.B
【分析】根据“大货车运输75吨货物所用车辆数与小货车运输50吨货物所用车辆数相同”即可列出方程.
【详解】解:设有大货车每辆运输x吨,则小货车每辆运输吨,
则.
故选B
【点拨】本题考查分式方程的应用,理解题意准确找到等量关系是解题的关键.
5.B
【分析】设乙车单独运送这批货物需x天,由题意列出分式方程即可求解.
【详解】解:设乙车单独运送这批货物需x天,由题意列方程
,
故选:B.
【点拨】本题考查了列分式方程,根据题意找到等量关系列出方程是解题的关键.
6.A
【分析】表示出第二批面粉的采购量,根据“每千克面粉价格提高了0.4元”这一等量关系即可列方程.
【详解】设第一批面粉采购量为x千克,则设第二批面粉采购量为千克,根据题意,得
故选:A
【点拨】本题考查列方程解决实际问题,找出题中的等量关系列出方程是解题的关键.
7.B
【分析】设出慢车的速度,再利用慢车的速度表示出快车的速度,根据所用时间差为1小时列方程即可.
【详解】解:设慢车的速度是,则快车的速度为,
依题意得,
故选:B.
【点拨】本题考查了由实际问题抽象出分式方程,找到关键描述语,找到等量关系是解决问题的关键.
8.B
【分析】根据题意可直接进行求解.
【详解】解:由题意得:;
故选:B.
【点拨】本题主要考查分式方程的应用,解题的关键是理解题意.
9.A
【分析】设购进的第一批“脆红李”的单价为x元/件,则购进第二批“脆红李”的单价为元/件,根据购进的第二批这种“脆红李”比第一批多购进了40件,列出方程即可.
【详解】解:设购进的第一批“脆红李”的单价为x元/件,则购进第二批“脆红李”的单价为元/件,根据题意得:
,故A正确.
故选:A.
【点拨】本题主要考查了分式方程的应用,解题的关键是找出题目中的等量关系式.
10.D
【分析】设乙同学的速度是米/分,根据乙同学比甲同学提前4分钟到达活动地点,列出方程即可.
【详解】解∶设乙同学的速度是米/分,可得:
故选∶ D.
【点拨】本题考查分式方程的应用,分析题意,找到合适的等量关系是解决问题的关键.
11.A
【分析】
设甲工程队每个月修x千米,则乙工程队每个月修千米,根据“最终用的时间比甲工程队少半个月”列出分式方程即可.
【详解】解:设甲工程队每个月修x千米,则乙工程队每个月修千米,
依题意得,
故选:A.
【点拨】此题主要考查了由实际问题抽象出分式方程,关键是分析题意,找准关键语句,列出相等关系.
12.B
【分析】根据提速前后所用时间相等列式即可.
【详解】解:根据题意,得.
故选:B.
【点拨】本题考查了列分式方程,找准等量关系是解题关键.
13.(1)
(2)125件
【分析】(1)根据“更新设备后生产效率比更新前提高了”列代数式即可;
(2)根据题意列分式方程,解方程即可.
【详解】(1)解:更新设备前每天生产x件产品,更新设备后生产效率比更新前提高了,
更新设备后每天生产产品数量为:(件),
故答案为:;
(2)解:由题意知:,
去分母,得,
解得,
经检验,是所列分式方程的解,
(件),
因此更新设备后每天生产125件产品.
【点拨】本题考查分式方程的实际应用,解题的关键是根据所给数量关系正确列出方程.
14.原计划每天种植梨树500棵
【分析】根据题意列出分式方程求解即可.
【详解】解:设原计划每天种植梨树x棵
由题可知:
解得:
经检验:是原方程的根,且符合题意.
答:原计划每天种植梨树500棵.
【点拨】题目注意考查分式方程的应用,理解题意列出分式方程是解题关键.
15.今年龙虾的平均亩产量.
【分析】设今年龙虾的平均亩产量是x,则去年龙虾的平均亩产量是,根据去年与今年的养殖面积相同列出分式方程,解方程并检验即可.
【详解】解:设今年龙虾的平均亩产量是x,则去年龙虾的平均亩产量是,
由题意得,,
解得,
经检验,是分式方程的解且符合题意,
答:今年龙虾的平均亩产量.
【点拨】此题考查了分式方程的实际应用,读懂题意,正确列出方程是解题的关键.
16.乙同学骑自行车的速度为千米/分钟.
【分析】设乙同学骑自行车的速度为x千米/分钟,则甲同学骑自行车的速度为千米/分钟,根据时间=路程÷速度结合甲车比乙车提前10分钟到达,即可得出关于x的分式方程,解之并检验后即可得出结论.
【详解】解:设乙同学骑自行车的速度为x千米/分钟,则甲同学骑自行车的速度为千米/分钟,
根据题意得:,
解得:.
经检验,是原方程的解,且符合题意,
答:乙同学骑自行车的速度为千米/分钟.
【点拨】题目主要考查分式方程的应用,理解题意列出分式方程是解题的关键.
17.(1)A型,B型玩具的单价分别是10元/个,15元/个
(2)最多可购进A型玩具25个
【分析】(1)设型玩具的单价为元/件.依题意列出分式方程,进行求解;
(2)根据题意列出不等式进行求解即可.
【详解】(1)设型玩具的单价为元/件.
由题意得:,
解得:
经检验,是原方程的解
B型玩具的单价为元/个
∴A型,B型玩具的单价分别是10元/个,15元/个.
(2)设购进A型玩具个.
解得:
∴最多可购进A型玩具25个.
【点拨】本题考查了分式方程,一元一次不等式的实际应用,解题的关键是根据题意列出相应的方程或不等式.
18.原计划平均每天制作个摆件.
【分析】设原计划平均每天制作个,根据题意列出方程,解方程即可求解.
【详解】解:设原计划平均每天制作个,根据题意得,
解得:
经检验,是原方程的解,且符合题意,
答:原计划平均每天制作个摆件.
【点拨】本题考查了分式方程的应用,根据题意列出方程是解题的关键.
19.乙每小时加工个这种零件.
【分析】设乙每小时加工个这种零件,则甲每小时加工个这种零件,利用“甲加工个这种零件所用的时间与乙加工个这种零件所用的时间相等”列分式方程即可求解.
【详解】解:设乙每小时加工个这种零件,则甲每小时加工个这种零件,
根据题意得:,
解得:,
经检验,是所列方程的解,且符合题意.
答:乙每小时加工个这种零件.
【点拨】本题主要考查了分式方程的应用,解题的关键在于能够根据题意找到等量关系列出方程进行求解.
20.甲路线的行驶时间为.
【分析】设甲路线的行驶时间为,则乙路线的行驶事件为,根据“甲路线的平均速度为乙路线的倍”列分式方程求解即可.
【详解】解:甲路线的行驶时间为,则乙路线的行驶事件为,由题意可得,
,
解得,
经检验是原方程的解,
∴甲路线的行驶时间为,
答:甲路线的行驶时间为.
【点拨】本题考查分式方程的应用,解题的关键是明确题意,找出等量关系列出相应的分式方程.
21..
【分析】设第一批足球单价为元,则第二批足球单价为元,再根据题意列出分式方程即可.
【详解】设第一批足球单价为元,则第二批足球单价为元,
由题意得:,
解得:,
经检验:是原分式方程的解,且符合题意,
则第二批足球单价为:,
∴该学校两批共购买了,
答:该学校两批共购买了个.
【点拨】此题考查了分式方程的应用,找准等量关系,正确列出分式方程是解题的关键.
22.(1)购买杂酱面80份,购买牛肉面90份
(2)购买牛肉面60份
【分析】(1)设购买杂酱面份,则购买牛肉面份,由题意知,,解方程可得的值,然后代入,计算求解,进而可得结果;
(2)设购买牛肉面份,则购买杂酱面份,由题意知,,计算求出满足要求的解即可.
【详解】(1)解:设购买杂酱面份,则购买牛肉面份,
由题意知,,
解得,,
∴,
∴购买杂酱面80份,购买牛肉面90份;
(2)解:设购买牛肉面份,则购买杂酱面份,
由题意知,,
解得,
经检验,是分式方程的解,
∴购买牛肉面60份.
【点拨】本题考查了一元一次方程的应用,分式方程的应用.解题的关键在于根据题意正确的列方程.
23.
【分析】根据甲、乙同学步行和骑自行车的速度之间的数量关系设未知数,再根据所走时间之间的数量关系列方程即可.
【详解】解:设甲同学步行的速度为,则乙同学骑自行车速度为,
,由题意得,
,
解得,
经检验,是分式方程的解,也符合实际.
,
答:乙同学骑自行车的速度为.
【点拨】本题考查了分式方程的实际应用,解决问题时需注意时间单位的统一,同时解分式方程需检验.
24.大型客车的速度为
【分析】设出慢车的速度,再利用慢车的速度表示出快车的速度,根据所用时间差为12分钟列方程解答.
【详解】解:设慢车的速度为,则快车的速度为,
根据题意得
,
解得:,
经检验,是原方程的根.
故大型客车的速度为.
【点拨】此题考查了分式方程的应用,分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键,此题的等量关系是快车与慢车所用时间差为12分钟.
25.这个学校九年级学生有300人.
【分析】设零售价为x元,批发价为y,然后根据题意列二元一次方程组求得零售价为12元,然后用3600除以零售价即可解答.
【详解】解:设零售价为x元,批发价为y,
根据题意可得:
,解得:,
经检验是原方程组的解
则学校九年级学生人.
答:这个学校九年级学生有300人.
【点拨】本题主要考查了二元一次方程组的应用,审清题意、列二元一次方程组求得零售价是解答本题的关键.
26.A品牌篮球单价为96元,B品牌篮球单价为72元
【分析】设B品牌篮球单价为x元,则A品牌篮球单价为元,,再利用“采购相同数量的A,B两种品牌篮球,分别需要花费9600元和7200元”,列方程,解方程即可.
【详解】解:设B品牌篮球单价为x元,则A品牌篮球单价为元,
根据题意,得.
解这个方程,得.
经检验,是所列方程的根.
(元).
所以,A品牌篮球单价为96元,B品牌篮球单价为72元.
【点拨】本题考查的是分式方程的应用,设出恰当的未知数,确定相等关系是解题的关键.
27.施工队原计划每天改造6米.
【分析】设施工队原计划每天改造米,根据提前2天成功地完成了大桥的改造任务得:,解方程并检验可得答案.
【详解】解:设施工队原计划每天改造米,
根据题意得:,
解得,
经检验,是原方程的解,
答:施工队原计划每天改造6米.
【点拨】本题考查分式方程的应用,解题的关键是读懂题意,找到等量关系列出分式方程.
28.乙班每小时挖400千克的土豆
【分析】设乙班每小时挖x千克的土豆,则甲班每小时挖(100+x)千克的土豆,根据题意列出分式方程即可求解.
【详解】设乙班每小时挖x千克的土豆,则甲班每小时挖(100+x)千克的土豆,
根据题意有:,
解得:x=400,
经检验,x=400是原方程的根,
故乙班每小时挖400千克的土豆.
【点拨】本题考查了分式方程的应用,明确题意列出分式方程是解答本题的关键.
29.A款套装的单价是180元、B款套装的单价是150元.
【分析】设B款套装的单价是x元,则A款套装的单价是1.2x元,即可得出关于x的分式方程,解之经检验后即可得出结论.
【详解】解:设B款套装的单价是x元,则A款套装的单价是1.2x元,
由题意得:,
解得:x=150,
经检验,x=150是原方程的解,且符合题意,
∴1.2x=180.
答:A款套装的单价是180元、B款套装的单价是150元.
【点拨】本题考查了分式方程的应用,解题的关键是:找准等量关系,正确列出分式方程.
30.(1)甲,乙两个商店租用的服装每套各50元,40元
(2)乙商店租用服装的费用较少,理由见解析
【分析】(1)解:设乙商店租用服装每套x元,则甲商店租用服装每套(x+10)元,由题意列,解分式方程并检验即可得出答案.
(2)分别计算甲、乙商店的费用,比较大小即可得出答案.
【详解】(1)解:设乙商店租用服装每套x元,则甲商店租用服装每套(x+10)元,
由题意可得:,
解得:x=40,
经检验,x=40是该分式方程的解,并符合题意,
∴x+10=50,
∴甲,乙两个商店租用的服装每套各50元,40元.
(2)解:乙商店租用服装的费用较少.
理由如下:
该参赛队伍准备租用20套服装时,甲商店的费用为:50×20×0.9=900(元),乙商店的费用为:40×20=800(元),
∵900>800,
∴乙商店租用服装的费用较少.
【点拨】本题主要考查了分式方程的应用,能够根据题意找出等量关系建立方程是解决本题的关键,但要注意分式方程的解需要进行检验.
31.160个
【分析】设李婷每分钟跳绳的个数为个,则刘芳每分钟跳绳的个数为个,根据“刘芳跳135个所用的时间与李婷跳120个所用的时间相等”建立方程,解方程即可得.
【详解】解:设李婷每分钟跳绳的个数为个,则刘芳每分钟跳绳的个数为个,
由题意得:,
解得,
经检验,是所列分式方程的解,且符合题意,
答:李婷每分钟跳绳的个数为160个.
【点拨】本题考查了分式方程的实际应用,正确找出等量关系,并建立方程是解题关键.
32.现在平均每天生产80个零件
【分析】设现在平均每天生产个零件,则原计划生产个零件,由题意得,,计算求出的值,然后进行检验即可.
【详解】解:设现在平均每天生产个零件,则原计划生产个零件,
由题意得,,
去分母得,,
移项合并得,,
系数化为1得,,
检验,将代入得,所以是原分式方程的解,
∴现在平均每天生产个零件.
【点拨】本题考查了分式方程的应用.解题的关键在于根据题意列分式方程.
33.摩托车的速度为40千米/时
【分析】设摩托车的速度为x千米/时,则抢修车的速度为1.5x千米/时,根据抢修车比摩托车少用10分钟,即可得出关于x的分式方程,解之经检验后即可得出结论.
【详解】解:设摩托车的速度为x千米/时,则抢修车的速度为1.5x千米/时,
依题意,得:,
解得:x=40,
经检验,x=40是所列方程的根,且符合题意,
答:摩托车的速度为40千米/时.
【点拨】本题考查了分式方程的应用,找准等量关系,正确列出分式方程是解题的关键.
34.每个小组有学生10名.
【分析】设每个小组有学生x名,根据题意列出方程,求出方程的解即可得到结果.
【详解】解:设每个小组有学生x名,
根据题意,得,
解这个方程,得x=10,
经检验,x=10是原方程的根,
∴每个小组有学生10名.
【点拨】此题考查了分式方程的应用,弄清题意是解本题的关键.
35.(1)
(2)千米/时
【分析】(1)设乙的速度为千米/时,则甲的速度为千米/时,根据甲出发半小时恰好追上乙列方程求解即可;
(2)设乙的速度为千米/时,则甲的速度为千米/时,根据甲、乙恰好同时到达地列方程求解即可.
【详解】(1)解:设乙的速度为千米/时,则甲的速度为千米/时,
由题意得:,
解得:,
则,
答:甲骑行的速度为千米/时;
(2)设乙的速度为千米/时,则甲的速度为千米/时,
由题意得:,
解得,
经检验是分式方程的解,
则,
答:甲骑行的速度为千米/时.
【点拨】本题考查了一元一次方程的应用和分式方程的应用,找准等量关系,正确列出方程是解题的关键.
36.(1)100米
(2)90米
【分析】(1)设甲施工队增加人员后每天修建灌溉水渠x米,原来每天修建米,根据工效问题公式:工作总量=工作时间×工作效率,列出关于x的一元一次方程,解方程即可得出答案;
(2)设乙施工队原来每天修建灌溉水渠y米,技术更新后每天修建米,根据水渠总长1800米,完工时,两施工队修建长度相同,可知每队修建900米,再结合两队同时开工修建,直至同时完工,可得两队工作时间相同,列出关于y的分式方程,解方程即可得出答案.
【详解】(1)解:设甲施工队增加人员后每天修建灌溉水渠x米,原来每天修建米,
则有
解得
∴甲施工队增加人员后每天修建灌溉水渠100米.
(2)∵水渠总长1800米,完工时,两施工队修建长度相同
∴两队修建的长度都为1800÷2=900(米)
乙施工队技术更新后,修建长度为900-360=540(米)
解:设乙施工队原来每天修建灌溉水渠y米,技术更新后每天修建米,即1.2y米
则有
解得
经检验,是原方程的解,符合题意
∴乙施工队原来每天修建灌溉水渠90米.
【点拨】本题考查一元一次方程和分式方程的实际应用,应注意分式方程要检验,读懂题意,正确设出未知数,并列出方程,是解题的关键.
37.张老师骑车的速度为千米/小时
【分析】实际应用题的解题步骤“设、列、解、答”,根据问题设未知数,找到题中等量关系张老师先走2小时,结果同时达到列分式方程,求解即可.
【详解】解:设张老师骑车的速度为千米/小时,则汽车速度是千米/小时,
根据题意得:,
解之得,
经检验是分式方程的解,
答:张老师骑车的速度为千米/小时.
【点拨】本题考查分式方程解实际应用题,根据问题设未知数,读懂题意,找到等量关系列出分式方程是解决问题的关键.
38.这款电动汽车平均每公里的充电费为0.2元.
【分析】设这款电动汽车平均每公里的充电费为x元,则燃油车平均每公里的充电费为(x+0.6)元,根据“电动汽车可行驶的总路程是燃油车的4倍”列分式方程,解方程即可求解.
【详解】解:设这款电动汽车平均每公里的充电费为x元.
根据题意,得.
解,得.
经检验,是原方程的根.
答:这款电动汽车平均每公里的充电费为0.2元.
【点拨】本题考查分式方程的应用,分析题意,找到合适的等量关系是解决问题的关键.
39.每个足球的进价是75元,每个篮球的进价是100元
【分析】设每个足球的进价是x元,则每个篮球的进价是(x+25)元,利用数量=总价÷单价,结合用2000元购进篮球的数量是用750元购进足球数量的2倍,即可得出关于x的分式方程,解之经检验后即可得出足球的单价,再将其代入(x+25)中即可求出篮球的单价.
【详解】解:设每个足球的进价是x元,
则每个篮球的进价是(x+25)元,
依题意得:=2×,
解得:x=75,
经检验,x=75是原方程的解,且符合题意,
∴x+25=75+25=100.
答:每个足球的进价是75元,每个篮球的进价是100元.
【点拨】本题考查了分式方程的应用,找准等量关系,正确列出分式方程是解题的关键.
40.小杰平均每分钟清点图书12本,小江平均每分钟清点图书15本
【分析】设小杰平均每分钟清点图书x本,则小江平均每分钟清点图书1.25x本,利用时间=清点图书的总数÷平均每分钟清点图书的数量,结合小江清点完600本图书比小杰清点完540本图书少用了5min,即可得出关于x的分式方程,解之经检验即可得出小杰平均每分钟清点图书数量,再将其代入1.25x中可求出小江平均每分钟清点图书数量.
【详解】解:设小杰平均每分钟清点图书x本,则小江平均每分钟清点图书1.25x本,
依题意得:﹣=5,
解得:x=12,
经检验,x=12是原方程的解,且符合题意,
∴1.25x=1.25×12=15.
答:小杰平均每分钟清点图书12本,小江平均每分钟清点图书15本.
【点拨】本题考查了分式方程的应用,找准等量关系,正确列出分式方程是解题的关键.
41.甲工程队每天改造的道路长度是80米,乙工程队每天改造的道路长度是60米.
【分析】根据题意列出方程求解即可.
【详解】解:设甲工程队每天改造的道路长度是x米,
列方程得:,
解得:x=80.
经检验,x=80是原分式方程的解
80-20=60.
答:甲工程队每天改造的道路长度是80米,乙工程队每天改造的道路长度是60米.
【点拨】此题考查了分式方程应用题的解法,解题的关键是根据题意找到等量关系并列出方程.
42.50
【分析】该商品打折卖出x件,找到等量关系即可.
【详解】解:该商品打折卖出x件
解得x=8
经检验:是原方程的解,且符合题意
∴商品打折前每件元
答:该商品打折前每件50元.
【点拨】此题考查分式方程实际问题中的销售问题,找到等量关系是解题的关键.
43.该景点在设施改造后平均每天用水2吨.
【分析】设该景点在设施改造后平均每天用水x吨,则原来平均每天用水2x吨,列出分式方程,即可求解.
【详解】解:设该景点在设施改造后平均每天用水x吨,则原来平均每天用水2x吨,
由题意得:,解得:x=2,
经检验:x=2是方程的解,且符合题意,
答:该景点在设施改造后平均每天用水2吨.
【点拨】本题主要考查分式方程的实际应用,找出等量关系,列出方程,是解题的关键.
44.(1)第一次每件的进价为50元;(2)两次的总利润为1700元.
【分析】(1)设第一次每件的进价为x元,则第二次进价为(1+20%)x,根据等量关系,列出分式方程,即可求解;
(2)根据总利润=总售价-总成本,列出算式,即可求解.
【详解】解:(1)设第一次每件的进价为x元,则第二次进价为(1+20%)x,
根据题意得:,解得:x=50,
经检验:x=50是方程的解,且符合题意,
答:第一次每件的进价为50元;
(2)(元),
答:两次的总利润为1700元.
【点拨】本题主要考查分式方程的实际应用,找准等量关系,列出分式方程,是解题的关键.
45.(1)小刚跑步的平均速度为150米/分;(2)小刚不能在上课前赶回学校,见解析
【分析】(1)根据题意,列出分式方程即可求得小刚的跑步平均速度;
(2)先求出小刚跑步和骑自行车的时间,加上取作业本和取自行车的时间,与上课时间20分钟作比较即可.
【详解】解:(1)设小刚跑步的平均速度为x米/分,则小刚骑自行车的平均速度为1.6x米/分,
根据题意,得,
解这个方程,得,
经检验,是所列方程的根,
所以小刚跑步的平均速度为150米/分.
(2)由(1)得小刚跑步的平均速度为150米/分,
则小刚跑步所用时间为(分),
骑自行车所用时间为(分),
在家取作业本和取自行车共用了3分,
所以小刚从开始跑步回家到赶回学校需要(分).
因为,
所以小刚不能在上课前赶回学校.
【点拨】本题考查路程问题的分式方程,解题关键是明确题意,列出分式方程求解.
46.2022年A,B两种经济作物分别种植20亩和10亩
【分析】设A,B两种经济作物分别种植x和(30-x)亩,根据B种经济作物亩产值比A种经济作物亩产值多2万元,建立分式方程即可求解.
【详解】解:设2022年A,B两种经济作物分别种植x和(30-x)亩,
由题意可知:A种经济作物亩产值为万元,
B种经济作物亩产值为万元,
由“B种经济作物亩产值比A种经济作物亩产值多2万元”可知:
=+,
解得:或(负值舍去),
经检验,当时原分式方程的分母不为0,
故2022年A,B两种经济作物分别种植20亩和10亩.
【点拨】本题考查了分式方程的应用,关键是要审题仔细,找到题中隐藏的等量关系进而建立方程求解.
47.每千克有机大米的售价为7元.
【分析】设每千克有机大米的售价为x元,则每千克普通大米的售价为(x-2)元,根据“用420元购买的有机大米与用300元购买的普通大米的重量相同”,列出分式方程,即可求解.
【详解】解:设每千克有机大米的售价为x元,则每千克普通大米的售价为(x-2)元,
根据题意得:,解得:x=7,
经检验:x=7是方程的解,且符合题意,
答:每千克有机大米的售价为7元.
【点拨】本题主要考查分式方程的实际应用,找准等量关系,列出分式方程,是解题的关键.
48.(1)甲种消毒液每桶的单价为30元,乙种消毒液每桶的单价为24元;(2)甲种消毒液购买75桶时,所需资金总额最少,最少总金额是4875元.
【分析】(1)根据该单位以零售价分别用900元和720元采购了相同桶数的甲、乙两种消毒液,可以得到相应的分式方程,从而可以得到甲、乙两种消毒剂的零售价,注意分式方程要检验;
(2)设购买甲种消毒液m桶,则购买乙种消毒液(300-m)桶,根据甲种消毒液的桶数不少于乙种消毒液桶数的,即可得出关于m的一元一次不等式,再结合费用总量列出一次函数,根据一次函数性质得出结果.
【详解】解:(1)设甲种消毒液每桶的单价为x元,乙种消毒液每桶的单价为(x-6)元,
依题意,得: ,
解得:x=30,
经检验,x=30是原方程的解,且符合实际意义,则x-6=24.
答:甲种消毒液每桶的单价为30元,乙种消毒液每桶的单价为24元;
(2)设购买甲种消毒液m桶,则购买乙种消毒液(300-m)桶,根据题意得到不等式:
m≥(300-m),解得:m≥75,
∴75≤m≤300,
设总费用为W,根据题意得:
W=20m+15(300-m)=5m+4500,
∵k=5>0,
∴W随m的减小而减小,
∴当m=75时,W有最小值,
∴W=5×75+4500=4875元
∴甲种消毒液购买75桶时,所需资金总额最少,最少总金额是4875元.
【点拨】本题考查一次函数的应用、分式方程的应用、一元一次不等式的应用,解答本题的关键是明确题意,利用一次函数的性质和不等式的性质解答,注意分式方程要检验.
49.(1)这种商品的单价为60元/件;(2)48,50;(3)金额
【分析】(1)根据题意设这种商品的单价为元/件,通过甲乙之间购买的商品数量间的数量关系列分式方程进行求解即可;
(2)利用两次购买总价÷两次购买总数量=平均单价,列式分别求出甲乙两次购买的平均单价即可;
(3)对比(2)中的计算数据总结即可得解.
【详解】(1)设这种商品的单价为元/件,
,解得,经检验是原分式方程的解,
则这种商品的单价为60元/件;
(2)甲,乙两人第二次再去采购该商品时,单价为元/件,
∵甲两次购买总价为元,购买总数量为件,
∴甲两次购买这种商品的平均单价是元/件;
∵乙两次购买总价为元,购买总数量为件,
∴乙两次购买这种商品的平均单价是元/件;
故答案为:48,50;
(3)∵,
∴按照甲两次购买商品的总价相同的情况下更合算,
∴建议按相同金额加油更合算,
故答案为:金额.
【点拨】本题主要考查了分式方程的实际应用,通过题目找准数量关系,利用总价÷数量=单价的基本等量关系式进行求解是解决本题的关键.
50.租用的A种客房每间客房的租金为200元,B种客房每间客房的租金为160元.
【分析】设租用的B种客房每间客房的租金为x元,根据用2000元租到A客房的数量与用1600元租到B客房的数量相等列出方程,解之即可.
【详解】解:设租用的B种客房每间客房的租金为x元,则A种客房每间客房的租金为x+40元,
由题意可得:,
解得:,
经检验:是原方程的解,
160+40=200元,
∴租用的A种客房每间客房的租金为200元,B种客房每间客房的租金为160元.
【点拨】本题考查了分式方程的实际应用,解题的关键是找准等量关系,列出方程.
一、单选题
1.(2023·四川内江·中考真题)用计算机处理数据,为了防止数据输入出错,某研究室安排两名程序操作员各输入一遍,比较两人的输入是否一致,本次操作需输入2640个数据,已知甲的输入速度是乙的2倍,结果甲比乙少用2小时输完.这两名操作员每分钟各能输入多少个数据?设乙每分钟能输入x个数据,根据题意得方程正确的是( )
A. B.
C. D.
2.(2023·湖北十堰·中考真题)为了落实“双减”政策,进一步丰富文体活动,学校准备购进一批篮球和足球,已知每个篮球的价格比每个足球的价格多20元,用1500元购进篮球的数量比用800元购进足球的数量多5个,如果设每个足球的价格为x元,那么可列方程为( )
A. B. C. D.
3.(2023·四川·中考真题)近年来,我市大力发展交通,建成多条快速通道,小张开车从家到单位有两条路线可选择,路线a为全程10千米的普通道路,路线b包含快速通道,全程7千米,走路线b比路线a平均速度提高,时间节省10分钟,求走路线a和路线b的平均速度分别是多少?设走路线a的平均速度为x千米/小时,依题意,可列方程为( )
A. B.
C. D.
4.(2023·广东深圳·中考真题)某运输公司运输一批货物,已知大货车比小货车每辆多运输5吨货物,且大货车运输75吨货物所用车辆数与小货车运输50吨货物所用车辆数相同,设有大货车每辆运输x吨,则所列方程正确的是( )
A. B. C. D.
5.(2023·黑龙江绥化·中考真题)某运输公司,运送一批货物,甲车每天运送货物总量的.在甲车运送1天货物后,公司增派乙车运送货物,两车又共同运送货物天,运完全部货物.求乙车单独运送这批货物需多少天?设乙车单独运送这批货物需x天,由题意列方程,正确的是( )
A. B.
C. D.
6.(2023·山东东营·中考真题)为扎实推进“五育”并举工作,加强劳动教育,东营市某中学针对七年级学生开设了“跟我学面点”烹饪课程,课程开设后学校花费6000元购进第一批面粉,用完后学校又花费9600元购进了第二批面粉,第二批面粉的采购量是第一批采购量的1.5倍,但每千克面粉价格提高了0.4元.设第一批面粉采购量为x千克,依题意所列方程正确的是( )
A. B.
C. D.
7.(2023·辽宁·中考真题)某校八年级学生去距离学校的游览区游览,一部分学生乘慢车先行,出发后,另一部分学生乘快车前往,结果他们同时到达.已知快车的速度是慢车速度的倍,求慢车的速度,设慢车的速度是,所列方程正确的是( )
A. B. C. D.
8.(2023·青海·中考真题)为了缅怀革命先烈,传承红色精神,青海省某学校八年级师生在清明节期间前往距离学校的烈士陵园扫墓.一部分师生骑自行车先走,过了后,其余师生乘汽车出发,结果他们同时到达;已知汽车的速度是骑车师生速度的2倍,设骑车师生的速度为.根据题意,下列方程正确的是( )
A. B. C. D.
9.(2023·四川达州·中考真题)某镇的“脆红李”深受广大市民的喜爱,也是馈赠亲友的尚佳礼品,首批“脆红李”成熟后,当地某电商用12000元购进这种“脆红李”进行销售,面市后,线上订单猛增供不应求,该电商又用11000元购进第二批这种“脆红李”,由于更多“脆红李”成熟,单价比第一批每件便宜了5元,但数量比第一批多购进了40件,求购进的第一批“脆红李”的单价.设购进的第一批“脆红李”的单价为x元/件,根据题意可列方程为( )
A. B.
C. D.
10.(2023·云南·中考真题)阅读,正如一束阳光.孩子们无论在哪儿,都可以感受到阳光的照耀,都可以通过阅读触及更广阔的世界.某区教育体育局向全区中小学生推出“童心读书会”的分享活动.甲、乙两同学分别从距离活动地点800米和400米的两地同时出发,参加分享活动.甲同学的速度是乙同学的速度的1.2倍,乙同学比甲同学提前4分钟到达活动地点.若设乙同学的速度是米/分,则下列方程正确的是( )
A. B. C. D.
11.(2023·湖北随州·中考真题)甲、乙两个工程队共同修一条道路,其中甲工程队需要修9千米,乙工程队需要修12千米.已知乙工程队每个月比甲工程队多修1千米,最终用的时间比甲工程队少半个月.若设甲工程队每个月修x千米,则可列出方程为( )
A. B. C. D.
12.(2023·广东广州·中考真题)随着城际交通的快速发展,某次动车平均提速60,动车提速后行驶480与提速前行驶360所用的时间相同.设动车提速后的平均速度为x,则下列方程正确的是( )
A. B. C. D.
二、解答题
13.(2023·贵州·中考真题)为推动乡村振兴,政府大力扶持小型企业.根据市场需求,某小型企业为加快生产速度,需要更新生产设备,更新设备后生产效率比更新前提高了,设更新设备前每天生产x件产品.解答下列问题:
(1)更新设备后每天生产_______件产品(用含x的式子表示);
(2)更新设备前生产5000件产品比更新设备后生产6000件产品多用2天,求更新设备后每天生产多少件产品.
14.(2023·四川乐山·中考真题)为了践行习近平总书记提出的“绿水青山就是金山银山”的发展理念,某地计划在规定时间内种植梨树棵.开始种植时,由于志愿者的加入,实际每天种植梨树的数量比原计划增加了,结果提前2天完成任务.问原计划每天种植梨树多少棵?
15.(2023·湖南岳阳·中考真题)水碧万物生,岳阳龙虾好.小龙虾产业已经成为岳阳乡村振兴的“闪亮名片”.已知翠翠家去年龙虾的总产量是,今年龙虾的总产量是,且去年与今年的养殖面积相同,平均亩产量去年比今年少,求今年龙虾的平均亩产量.
16.(2023·广东·中考真题)某学校开展了社会实践活动,活动地点距离学校,甲、乙两同学骑自行车同时从学校出发,甲的速度是乙的倍,结果甲比乙早到,求乙同学骑自行车的速度.
17.(2023·湖南常德·中考真题)“六一”儿童节将至,张老板计划购买A型玩具和B型玩具进行销售,若用1200元购买A型玩具的数量比用1500元购买B型玩具的数量多20个,且一个B型玩具的进价是一个A型玩具进价的1.5倍.
(1)求A型玩具和B型玩具的进价分别是多少?
(2)若A型玩具的售价为12元/个,B型玩具的售价为20元/个,张老板购进A,B型玩具共75个,要使总利润不低于300元,则A型玩具最多购进多少个?
18.(2023·吉林长春·中考真题)随着中国网民规模突破亿、博物馆美育不断向线上拓展.敦煌研究院顺势推出数字敦煌文化大使伽瑶,受到广大敦煌文化爱好者的好评.某工厂计划制作个伽瑶玩偶摆件,为了尽快完成任务,实际平均每天完成的数量是原计划的倍,结果提前天完成任务.问原计划平均每天制作多少个摆件?
19.(2023·辽宁沈阳·中考真题)甲、乙两人加工同一种零件,每小时甲比乙多加工个这种零件,甲加工个这种零件所用的时间与乙加工个这种零件所用的时间相等,求乙每小时加工多少个这种零件.
20.(2023·江苏徐州·中考真题)随着2022年底城东快速路的全线通车,徐州主城区与东区之间的交通得以有效改善,如图某人乘车从徐州东站至戏马台景区,可沿甲路线或乙路线前往.已知甲、乙两条路线的长度均为,甲路线的平均速度为乙路线的倍,甲路线的行驶时间比乙路线少,求甲路线的行驶时间.
21.(2023·黑龙江大庆·中考真题)为营造良好体育运动氛围,某学校用元购买了一批足球,又用元加购了第二批足球,且所购数量是第一批购买数量的倍,但单价降了元,请问该学校两批共购买了多少个足球
22.(2023·重庆·中考真题)某公司不定期为员工购买某预制食品厂生产的杂酱面、牛肉面两种食品.
(1)该公司花费3000元一次性购买了杂酱面、牛肉面共170份,此时杂酱面、牛肉面的价格分别为15元、20元,求购买两种食品各多少份?
(2)由于公司员工人数和食品价格有所调整,现该公司分别花费1260元、1200元一次性购买杂酱面、牛肉面两种食品,已知购买杂酱面的份数比牛肉面的份数多,每份杂酱面比每份牛肉面的价格少6元,求购买牛肉面多少份?
23.(2023·江苏扬州·中考真题)甲、乙两名学生到离校的“人民公园”参加志愿者活动,甲同学步行,乙同学骑自行车,骑自行车速度是步行速度的4倍,甲出发后乙同学出发,两名同学同时到达,求乙同学骑自行车的速度.
24.(2023·山东·中考真题)某校组织学生去郭永怀纪念馆进行研学活动.纪念馆距学校72千米,部分学生乘坐大型客车先行,出发12分钟后,另一部分学生乘坐小型客车前往,结果同时到达.已知小型客车的速度是大型客车速度的倍,求大型客车的速度.
25.(2023·山东泰安·中考真题)为进行某项数学综合与实践活动,小明到一个批发兼零售的商店购买所需工具.该商店规定一次性购买该工具达到一定数量后可以按批发价付款,否则按零售价付款.小明如果给学校九年级学生每人购买一个,只能按零售价付款,需用3600元;如果多购买60个,则可以按批发价付款,同样需用3600元,若按批发价购买60个与按零售价购买50个所付款相同,求这个学校九年级学生有多少人?
26.(2023·辽宁锦州·中考真题)2023年5月15日,辽宁男篮取得第三次CBA总冠军,辽篮运动员的拼搏精神感染了众多球迷.某校篮球社团人数迅增,急需购进A,B两种品牌篮球,已知A品牌篮球单价比B品牌篮球单价的2倍少48元,采购相同数量的A,B两种品牌篮球,分别需要花费9600元和7200元.求A,B两种品牌篮球的单价分别是多少元?
27.(2023·辽宁丹东·中考真题)“畅通交通,扮靓城市”,某市在道路提升改造中,将一座长度为36米的桥梁进行重新改造.为了尽快通车,某施工队在实际施工时,每天工作效率比原计划提高了,结果提前2天成功地完成了大桥的改造任务,那么该施工队原计划每天改造多少米
28.(2022·吉林长春·中考真题)为了让学生崇尚劳动,尊重劳动,在劳动中提升综合素质,某校定期开展劳动实践活动.甲、乙两班在一次体验挖土豆的活动中,甲班挖1500千克土豆与乙班挖1200千克土豆所用的时间相同.已知甲班平均每小时比乙班多挖100千克土豆,问乙班平均每小时挖多少千克土豆?
29.(2022·辽宁·中考真题)2022年3月23日“天宫课堂”第二课在中国空间站开讲了,精彩的直播激发了学生探索科学奥秘的兴趣.某中学为满足学生的需求,充实物理兴趣小组的实验项目,决定购入A、B两款物理实验套装,其中A款套装单价是B款套装单价的1.2倍,用9900元购买的A款套装数量比用7500元购买的B款套装数量多5套.求A、B两款套装的单价分别是多少元.
30.(2022·广西桂林·中考真题)今年,某市举办了一届主题为“强国复兴有我”的中小学课本剧比赛.某队伍为参赛需租用一批服装,经了解,在甲商店租用服装比在乙商店租用服装每套多10元,用500元在甲商店租用服装的数量与用400元在乙商店租用服装的数量相等.
(1)求在甲,乙两个商店租用的服装每套各多少元?
(2)若租用10套以上服装,甲商店给以每套九折优惠.该参赛队伍准备租用20套服装,请问在哪家商店租用服装的费用较少,并说明理由.
31.(2022·吉林·中考真题)刘芳和李婷进行跳绳比赛.已知刘芳每分钟比李婷多跳20个,刘芳跳135个所用的时间与李婷跳120个所用的时间相等.求李婷每分钟跳绳的个数.
32.(2022·黑龙江大庆·中考真题)某工厂生产某种零件,由于技术上的改进,现在平均每天比原计划多生产20个零件,现在生产800个零件所需时间与原计划生产600个零件所需时间相同.求现在平均每天生产多少个零件?
33.(2022·四川乐山·中考真题)第十四届四川省运动会定于2022年8月8日在乐山市举办,为保证省运会期间各场馆用电设施的正常运行,市供电局为此进行了电力抢修演练.现抽调区县电力维修工人到20千米远的市体育馆进行电力抢修.维修工人骑摩托车先行出发,10分钟后,抢修车装载完所需材料再出发,结果他们同时到达体育馆,已知抢修车是摩托车速度的1.5倍,求摩托车的速度.
34.(2022·江苏扬州·中考真题)某中学为准备十四岁青春仪式,原计划由八年级(1)班的4个小组制作360面彩旗,后因1个小组另有任务,其余3个小组的每名学生要比原计划多做3面彩旗才能完成任务.如果这4个小组的人数相等,那么每个小组有学生多少名?
35.(2022·重庆·中考真题)在全民健身运动中,骑行运动颇受市民青睐,甲、乙两骑行爱好者约定从地沿相同路线骑行去距地30千米的地,已知甲骑行的速度是乙的1.2倍.
(1)若乙先骑行2千米,甲才开始从地出发,则甲出发半小时恰好追上乙,求甲骑行的速度;
(2)若乙先骑行20分钟,甲才开始从地出发,则甲、乙恰好同时到达地,求甲骑行的速度.
36.(2022·重庆·中考真题)为保障蔬菜基地种植用水,需要修建灌溉水渠.
(1)计划修建灌溉水渠600米,甲施工队施工5天后,增加施工人员,每天比原来多修建20米,再施工2天完成任务,求甲施工队增加人员后每天修建灌溉水渠多少米?
(2)因基地面积扩大,现还需修建另一条灌溉水渠1800米,为早日完成任务,决定派乙施工队与甲施工队同时开工合作修建这条水渠,直至完工.甲施工队按(1)中增加人员后的修建速度进行施工.乙施工队修建360米后,通过技术更新,每天比原来多修建20%,灌溉水渠完工时,两施工队修建的长度恰好相同.求乙施工队原来每天修建灌溉水渠多少米?
37.(2022·四川自贡·中考真题)学校师生去距学校45千米的吴玉章故居开展研学活动,骑行爱好者张老师骑自行车先行2小时后,其余师生乘汽车出发,结果同时到达;已知汽车速度是自行车速度的3倍,求张老师骑车的速度.
38.(2022·山西·中考真题)2022年我国已成为全球最大的电动汽车市场,电动汽车在保障能源安全,改善空气质量等方面较传统汽车都有明显优势,经过对某款电动汽车和某款燃油车的对比调查发现,电动汽车平均每公里的充电费比燃油车平均每公里的加油费少0.6元.若充电费和加油费均为200元时,电动汽车可行驶的总路程是燃油车的4倍,求这款电动汽车平均每公里的充电费.
39.(2021·辽宁朝阳·中考真题)为了进一步丰富校园文体活动,学校准备购进一批篮球和足球,已知每个篮球的进价比每个足球的进价多25元,用2000元购进篮球的数量是用750元购进足球数量的2倍,求:每个篮球和足球的进价各多少元?
40.(2021·辽宁锦州·中考真题)小江与小杰两名同学为学校图书馆清点一批图书,小江清点完600本图书比小杰清点完540本图书少用了5min.已知小江平均每分钟清点图书的数量是小杰的1.25倍,求两名同学平均每分钟清点图书各多少本.
41.(2021·辽宁丹东·中考真题)为落实“乡村振兴计划”的工作要求,某区政府计划对乡镇道路进行改造,安排甲、乙两个工程队完成,已知乙队比甲队每天少改造20米,甲队改造400米的道路与乙队改造300米的道路所用时间相同,求甲、乙两个工程队每天改造的道路长度分别是多少米?
42.(2021·江苏徐州·中考真题)某网店开展促销活动,其商品一律按8折销售,促销期间用400元在该网店购得某商品的数量较打折前多出2件.问:该商品打折前每件多少元?
43.(2021·江苏常州·中考真题)为落实节约用水的政策,某旅游景点进行设施改造,将手拧水龙头全部更换成感应水龙头.已知该景点在设施改造后,平均每天用水量是原来的一半,20吨水可以比原来多用5天,该景点在设施改造后平均每天用水多少吨?
44.(2021·山东威海·中考真题)六一儿童节来临之际,某商店用3000元购进一批玩具,很快售完;第二次购进时,每件的进价提高了20%,同样用3000元购进的数量比第一次少了10件.
(1)求第一次每件的进价为多少元?
(2)若两次购进的玩具售价均为70元,且全部售完,求两次的总利润为多少元?
45.(2021·内蒙古·中考真题)小刚家到学校的距离是1800米.某天早上,小刚到学校后发现作业本忘在家中,此时离上课还有20分钟,于是他立即按原路跑步回家,拿到作业本后骑自行车按原路返回学校.已知小刚骑自行车时间比跑步时间少用了4.5分钟,且骑自行车的平均速度是跑步的平均速度的1.6倍.
(1)求小刚跑步的平均速度;
(2)如果小刚在家取作业本和取自行车共用了3分钟,他能否在上课前赶回学校?请说明理由.
46.(2021·湖南永州·中考真题)永州市某村经济合作社在乡村振兴工作队的指导下,根据市场需求,计划在2022年将30亩土地全部用于种植A,B两种经济作物.预计B种经济作物亩产值比A种经济作物亩产值多2万元,为实现2022年A种经济作物年总产值20万元,B种经济作物年总产值30万元的目标,问:2022年A,B两种经济作物应各种植多少亩?
47.(2021·吉林长春·中考真题)为助力乡村发展,某购物平台推出有机大米促销活动,其中每千克有机大米的售价仅比普通大米多2元,用420元购买的有机大米与用300元购买的普通大米的重量相同,求每千克有机大米的售价为多少元?
48.(2021·内蒙古通辽·中考真题)为做好新冠疫情的防控工作,某单位需购买甲、乙两种消毒液经了解每桶甲种消毒液的零售价比乙种消毒液的零售价多6元,该单位以零售价分别用900元和720元采购了相同桶数的甲、乙两种消毒液.
(1)求甲、乙两种消毒液的零售价分别是每桶多少元?
(2)由于疫情防控进入常态化,该单位需再次购买两种消毒液共300桶,且甲种消毒液的桶数不少于乙种消毒液桶数的,由于购买量大,甲、乙两种消毒液分别获得了20元/桶,15元/桶的批发价.求甲种消毒液购买多少桶时,所需资金总额最少?最少总金额是多少元?
49.(2021·江西·中考真题)甲,乙两人去市场采购相同价格的同一种商品,甲用2400元购买的商品数量比乙用3000元购买的商品数量少10件.
(1)求这种商品的单价;
(2)甲,乙两人第二次再去采购该商品时,单价比上次少了20元/件,甲购买商品的总价与上次相同,乙购买商品的数量与上次相同,则甲两次购买这种商品的平均单价是______元/件,乙两次购买这种商品的平均单价是______元/件.
(3)生活中,无论油价如何变化,有人总按相同金额加油,有人总按相同油量加油,结合(2)的计算结果,建议按相同______加油更合算(填“金额”或“油量”).
50.(2021·云南·中考真题)“30天无理由退货”是营造我省“诚信旅游”良好环境,进一步提升旅游形象的创新举措.机场、车站、出租车、景区、手机短信……,“30天无理由退货”的提示随处可见,它已成为一张云南旅行的“安心卡”,极大地提高了旅游服务的品质.刚刚过去的“五·一”假期,旅游线路、住宿、餐饮、生活服务、购物等旅游消费的供给更加多元,同步的是云南旅游市场强劲复苏.某旅行社今年5月1日租用A、B两种客房一天,供当天使用.下面是有关信息:今天用2000元租到A客房的数量与用1600元租到B客房的数量相等.今天每间A客房的租金比每间B客房的租金多40元.请根据上述信息,分别求今年5月1日该旅行社租用的A、B两种客房每间客房的租金.
中小学教育资源及组卷应用平台
试卷第1页,共3页
参考答案:
1.D
【分析】设乙每分钟能输入x个数据,则甲每分钟能输入个数据,根据“甲比乙少用2小时输完”列出分式方程即可.
【详解】解:设乙每分钟能输入x个数据,则甲每分钟能输入个数据,
由题意得,
故选:D.
【点拨】本题考查了由实际问题抽象出分式方程,找准等量关系,正确列出分式方程是解题的关键.
2.A
【分析】设每个足球的价格为x元,则篮球的价格为元,根据“用1500元购进篮球的数量比用800元购进足球的数量多5个”列方程即可.
【详解】解:设每个足球的价格为x元,则篮球的价格为元,
由题意可得:,
故选:A.
【点拨】本题考查分式方程的应用,正确理解题意是关键.
3.A
【分析】若设路线a时的平均速度为x千米/小时,则走路线b时的平均速度为千米/小时,根据路线b的全程比路线a少用10分钟可列出方程.
【详解】解:由题意可得走路线b时的平均速度为千米/小时,
∴,
故选:A.
【点拨】本题考查了由实际问题抽象出分式方程,找到关键描述语,找到合适的等量关系是解决问题的关键.
4.B
【分析】根据“大货车运输75吨货物所用车辆数与小货车运输50吨货物所用车辆数相同”即可列出方程.
【详解】解:设有大货车每辆运输x吨,则小货车每辆运输吨,
则.
故选B
【点拨】本题考查分式方程的应用,理解题意准确找到等量关系是解题的关键.
5.B
【分析】设乙车单独运送这批货物需x天,由题意列出分式方程即可求解.
【详解】解:设乙车单独运送这批货物需x天,由题意列方程
,
故选:B.
【点拨】本题考查了列分式方程,根据题意找到等量关系列出方程是解题的关键.
6.A
【分析】表示出第二批面粉的采购量,根据“每千克面粉价格提高了0.4元”这一等量关系即可列方程.
【详解】设第一批面粉采购量为x千克,则设第二批面粉采购量为千克,根据题意,得
故选:A
【点拨】本题考查列方程解决实际问题,找出题中的等量关系列出方程是解题的关键.
7.B
【分析】设出慢车的速度,再利用慢车的速度表示出快车的速度,根据所用时间差为1小时列方程即可.
【详解】解:设慢车的速度是,则快车的速度为,
依题意得,
故选:B.
【点拨】本题考查了由实际问题抽象出分式方程,找到关键描述语,找到等量关系是解决问题的关键.
8.B
【分析】根据题意可直接进行求解.
【详解】解:由题意得:;
故选:B.
【点拨】本题主要考查分式方程的应用,解题的关键是理解题意.
9.A
【分析】设购进的第一批“脆红李”的单价为x元/件,则购进第二批“脆红李”的单价为元/件,根据购进的第二批这种“脆红李”比第一批多购进了40件,列出方程即可.
【详解】解:设购进的第一批“脆红李”的单价为x元/件,则购进第二批“脆红李”的单价为元/件,根据题意得:
,故A正确.
故选:A.
【点拨】本题主要考查了分式方程的应用,解题的关键是找出题目中的等量关系式.
10.D
【分析】设乙同学的速度是米/分,根据乙同学比甲同学提前4分钟到达活动地点,列出方程即可.
【详解】解∶设乙同学的速度是米/分,可得:
故选∶ D.
【点拨】本题考查分式方程的应用,分析题意,找到合适的等量关系是解决问题的关键.
11.A
【分析】
设甲工程队每个月修x千米,则乙工程队每个月修千米,根据“最终用的时间比甲工程队少半个月”列出分式方程即可.
【详解】解:设甲工程队每个月修x千米,则乙工程队每个月修千米,
依题意得,
故选:A.
【点拨】此题主要考查了由实际问题抽象出分式方程,关键是分析题意,找准关键语句,列出相等关系.
12.B
【分析】根据提速前后所用时间相等列式即可.
【详解】解:根据题意,得.
故选:B.
【点拨】本题考查了列分式方程,找准等量关系是解题关键.
13.(1)
(2)125件
【分析】(1)根据“更新设备后生产效率比更新前提高了”列代数式即可;
(2)根据题意列分式方程,解方程即可.
【详解】(1)解:更新设备前每天生产x件产品,更新设备后生产效率比更新前提高了,
更新设备后每天生产产品数量为:(件),
故答案为:;
(2)解:由题意知:,
去分母,得,
解得,
经检验,是所列分式方程的解,
(件),
因此更新设备后每天生产125件产品.
【点拨】本题考查分式方程的实际应用,解题的关键是根据所给数量关系正确列出方程.
14.原计划每天种植梨树500棵
【分析】根据题意列出分式方程求解即可.
【详解】解:设原计划每天种植梨树x棵
由题可知:
解得:
经检验:是原方程的根,且符合题意.
答:原计划每天种植梨树500棵.
【点拨】题目注意考查分式方程的应用,理解题意列出分式方程是解题关键.
15.今年龙虾的平均亩产量.
【分析】设今年龙虾的平均亩产量是x,则去年龙虾的平均亩产量是,根据去年与今年的养殖面积相同列出分式方程,解方程并检验即可.
【详解】解:设今年龙虾的平均亩产量是x,则去年龙虾的平均亩产量是,
由题意得,,
解得,
经检验,是分式方程的解且符合题意,
答:今年龙虾的平均亩产量.
【点拨】此题考查了分式方程的实际应用,读懂题意,正确列出方程是解题的关键.
16.乙同学骑自行车的速度为千米/分钟.
【分析】设乙同学骑自行车的速度为x千米/分钟,则甲同学骑自行车的速度为千米/分钟,根据时间=路程÷速度结合甲车比乙车提前10分钟到达,即可得出关于x的分式方程,解之并检验后即可得出结论.
【详解】解:设乙同学骑自行车的速度为x千米/分钟,则甲同学骑自行车的速度为千米/分钟,
根据题意得:,
解得:.
经检验,是原方程的解,且符合题意,
答:乙同学骑自行车的速度为千米/分钟.
【点拨】题目主要考查分式方程的应用,理解题意列出分式方程是解题的关键.
17.(1)A型,B型玩具的单价分别是10元/个,15元/个
(2)最多可购进A型玩具25个
【分析】(1)设型玩具的单价为元/件.依题意列出分式方程,进行求解;
(2)根据题意列出不等式进行求解即可.
【详解】(1)设型玩具的单价为元/件.
由题意得:,
解得:
经检验,是原方程的解
B型玩具的单价为元/个
∴A型,B型玩具的单价分别是10元/个,15元/个.
(2)设购进A型玩具个.
解得:
∴最多可购进A型玩具25个.
【点拨】本题考查了分式方程,一元一次不等式的实际应用,解题的关键是根据题意列出相应的方程或不等式.
18.原计划平均每天制作个摆件.
【分析】设原计划平均每天制作个,根据题意列出方程,解方程即可求解.
【详解】解:设原计划平均每天制作个,根据题意得,
解得:
经检验,是原方程的解,且符合题意,
答:原计划平均每天制作个摆件.
【点拨】本题考查了分式方程的应用,根据题意列出方程是解题的关键.
19.乙每小时加工个这种零件.
【分析】设乙每小时加工个这种零件,则甲每小时加工个这种零件,利用“甲加工个这种零件所用的时间与乙加工个这种零件所用的时间相等”列分式方程即可求解.
【详解】解:设乙每小时加工个这种零件,则甲每小时加工个这种零件,
根据题意得:,
解得:,
经检验,是所列方程的解,且符合题意.
答:乙每小时加工个这种零件.
【点拨】本题主要考查了分式方程的应用,解题的关键在于能够根据题意找到等量关系列出方程进行求解.
20.甲路线的行驶时间为.
【分析】设甲路线的行驶时间为,则乙路线的行驶事件为,根据“甲路线的平均速度为乙路线的倍”列分式方程求解即可.
【详解】解:甲路线的行驶时间为,则乙路线的行驶事件为,由题意可得,
,
解得,
经检验是原方程的解,
∴甲路线的行驶时间为,
答:甲路线的行驶时间为.
【点拨】本题考查分式方程的应用,解题的关键是明确题意,找出等量关系列出相应的分式方程.
21..
【分析】设第一批足球单价为元,则第二批足球单价为元,再根据题意列出分式方程即可.
【详解】设第一批足球单价为元,则第二批足球单价为元,
由题意得:,
解得:,
经检验:是原分式方程的解,且符合题意,
则第二批足球单价为:,
∴该学校两批共购买了,
答:该学校两批共购买了个.
【点拨】此题考查了分式方程的应用,找准等量关系,正确列出分式方程是解题的关键.
22.(1)购买杂酱面80份,购买牛肉面90份
(2)购买牛肉面60份
【分析】(1)设购买杂酱面份,则购买牛肉面份,由题意知,,解方程可得的值,然后代入,计算求解,进而可得结果;
(2)设购买牛肉面份,则购买杂酱面份,由题意知,,计算求出满足要求的解即可.
【详解】(1)解:设购买杂酱面份,则购买牛肉面份,
由题意知,,
解得,,
∴,
∴购买杂酱面80份,购买牛肉面90份;
(2)解:设购买牛肉面份,则购买杂酱面份,
由题意知,,
解得,
经检验,是分式方程的解,
∴购买牛肉面60份.
【点拨】本题考查了一元一次方程的应用,分式方程的应用.解题的关键在于根据题意正确的列方程.
23.
【分析】根据甲、乙同学步行和骑自行车的速度之间的数量关系设未知数,再根据所走时间之间的数量关系列方程即可.
【详解】解:设甲同学步行的速度为,则乙同学骑自行车速度为,
,由题意得,
,
解得,
经检验,是分式方程的解,也符合实际.
,
答:乙同学骑自行车的速度为.
【点拨】本题考查了分式方程的实际应用,解决问题时需注意时间单位的统一,同时解分式方程需检验.
24.大型客车的速度为
【分析】设出慢车的速度,再利用慢车的速度表示出快车的速度,根据所用时间差为12分钟列方程解答.
【详解】解:设慢车的速度为,则快车的速度为,
根据题意得
,
解得:,
经检验,是原方程的根.
故大型客车的速度为.
【点拨】此题考查了分式方程的应用,分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键,此题的等量关系是快车与慢车所用时间差为12分钟.
25.这个学校九年级学生有300人.
【分析】设零售价为x元,批发价为y,然后根据题意列二元一次方程组求得零售价为12元,然后用3600除以零售价即可解答.
【详解】解:设零售价为x元,批发价为y,
根据题意可得:
,解得:,
经检验是原方程组的解
则学校九年级学生人.
答:这个学校九年级学生有300人.
【点拨】本题主要考查了二元一次方程组的应用,审清题意、列二元一次方程组求得零售价是解答本题的关键.
26.A品牌篮球单价为96元,B品牌篮球单价为72元
【分析】设B品牌篮球单价为x元,则A品牌篮球单价为元,,再利用“采购相同数量的A,B两种品牌篮球,分别需要花费9600元和7200元”,列方程,解方程即可.
【详解】解:设B品牌篮球单价为x元,则A品牌篮球单价为元,
根据题意,得.
解这个方程,得.
经检验,是所列方程的根.
(元).
所以,A品牌篮球单价为96元,B品牌篮球单价为72元.
【点拨】本题考查的是分式方程的应用,设出恰当的未知数,确定相等关系是解题的关键.
27.施工队原计划每天改造6米.
【分析】设施工队原计划每天改造米,根据提前2天成功地完成了大桥的改造任务得:,解方程并检验可得答案.
【详解】解:设施工队原计划每天改造米,
根据题意得:,
解得,
经检验,是原方程的解,
答:施工队原计划每天改造6米.
【点拨】本题考查分式方程的应用,解题的关键是读懂题意,找到等量关系列出分式方程.
28.乙班每小时挖400千克的土豆
【分析】设乙班每小时挖x千克的土豆,则甲班每小时挖(100+x)千克的土豆,根据题意列出分式方程即可求解.
【详解】设乙班每小时挖x千克的土豆,则甲班每小时挖(100+x)千克的土豆,
根据题意有:,
解得:x=400,
经检验,x=400是原方程的根,
故乙班每小时挖400千克的土豆.
【点拨】本题考查了分式方程的应用,明确题意列出分式方程是解答本题的关键.
29.A款套装的单价是180元、B款套装的单价是150元.
【分析】设B款套装的单价是x元,则A款套装的单价是1.2x元,即可得出关于x的分式方程,解之经检验后即可得出结论.
【详解】解:设B款套装的单价是x元,则A款套装的单价是1.2x元,
由题意得:,
解得:x=150,
经检验,x=150是原方程的解,且符合题意,
∴1.2x=180.
答:A款套装的单价是180元、B款套装的单价是150元.
【点拨】本题考查了分式方程的应用,解题的关键是:找准等量关系,正确列出分式方程.
30.(1)甲,乙两个商店租用的服装每套各50元,40元
(2)乙商店租用服装的费用较少,理由见解析
【分析】(1)解:设乙商店租用服装每套x元,则甲商店租用服装每套(x+10)元,由题意列,解分式方程并检验即可得出答案.
(2)分别计算甲、乙商店的费用,比较大小即可得出答案.
【详解】(1)解:设乙商店租用服装每套x元,则甲商店租用服装每套(x+10)元,
由题意可得:,
解得:x=40,
经检验,x=40是该分式方程的解,并符合题意,
∴x+10=50,
∴甲,乙两个商店租用的服装每套各50元,40元.
(2)解:乙商店租用服装的费用较少.
理由如下:
该参赛队伍准备租用20套服装时,甲商店的费用为:50×20×0.9=900(元),乙商店的费用为:40×20=800(元),
∵900>800,
∴乙商店租用服装的费用较少.
【点拨】本题主要考查了分式方程的应用,能够根据题意找出等量关系建立方程是解决本题的关键,但要注意分式方程的解需要进行检验.
31.160个
【分析】设李婷每分钟跳绳的个数为个,则刘芳每分钟跳绳的个数为个,根据“刘芳跳135个所用的时间与李婷跳120个所用的时间相等”建立方程,解方程即可得.
【详解】解:设李婷每分钟跳绳的个数为个,则刘芳每分钟跳绳的个数为个,
由题意得:,
解得,
经检验,是所列分式方程的解,且符合题意,
答:李婷每分钟跳绳的个数为160个.
【点拨】本题考查了分式方程的实际应用,正确找出等量关系,并建立方程是解题关键.
32.现在平均每天生产80个零件
【分析】设现在平均每天生产个零件,则原计划生产个零件,由题意得,,计算求出的值,然后进行检验即可.
【详解】解:设现在平均每天生产个零件,则原计划生产个零件,
由题意得,,
去分母得,,
移项合并得,,
系数化为1得,,
检验,将代入得,所以是原分式方程的解,
∴现在平均每天生产个零件.
【点拨】本题考查了分式方程的应用.解题的关键在于根据题意列分式方程.
33.摩托车的速度为40千米/时
【分析】设摩托车的速度为x千米/时,则抢修车的速度为1.5x千米/时,根据抢修车比摩托车少用10分钟,即可得出关于x的分式方程,解之经检验后即可得出结论.
【详解】解:设摩托车的速度为x千米/时,则抢修车的速度为1.5x千米/时,
依题意,得:,
解得:x=40,
经检验,x=40是所列方程的根,且符合题意,
答:摩托车的速度为40千米/时.
【点拨】本题考查了分式方程的应用,找准等量关系,正确列出分式方程是解题的关键.
34.每个小组有学生10名.
【分析】设每个小组有学生x名,根据题意列出方程,求出方程的解即可得到结果.
【详解】解:设每个小组有学生x名,
根据题意,得,
解这个方程,得x=10,
经检验,x=10是原方程的根,
∴每个小组有学生10名.
【点拨】此题考查了分式方程的应用,弄清题意是解本题的关键.
35.(1)
(2)千米/时
【分析】(1)设乙的速度为千米/时,则甲的速度为千米/时,根据甲出发半小时恰好追上乙列方程求解即可;
(2)设乙的速度为千米/时,则甲的速度为千米/时,根据甲、乙恰好同时到达地列方程求解即可.
【详解】(1)解:设乙的速度为千米/时,则甲的速度为千米/时,
由题意得:,
解得:,
则,
答:甲骑行的速度为千米/时;
(2)设乙的速度为千米/时,则甲的速度为千米/时,
由题意得:,
解得,
经检验是分式方程的解,
则,
答:甲骑行的速度为千米/时.
【点拨】本题考查了一元一次方程的应用和分式方程的应用,找准等量关系,正确列出方程是解题的关键.
36.(1)100米
(2)90米
【分析】(1)设甲施工队增加人员后每天修建灌溉水渠x米,原来每天修建米,根据工效问题公式:工作总量=工作时间×工作效率,列出关于x的一元一次方程,解方程即可得出答案;
(2)设乙施工队原来每天修建灌溉水渠y米,技术更新后每天修建米,根据水渠总长1800米,完工时,两施工队修建长度相同,可知每队修建900米,再结合两队同时开工修建,直至同时完工,可得两队工作时间相同,列出关于y的分式方程,解方程即可得出答案.
【详解】(1)解:设甲施工队增加人员后每天修建灌溉水渠x米,原来每天修建米,
则有
解得
∴甲施工队增加人员后每天修建灌溉水渠100米.
(2)∵水渠总长1800米,完工时,两施工队修建长度相同
∴两队修建的长度都为1800÷2=900(米)
乙施工队技术更新后,修建长度为900-360=540(米)
解:设乙施工队原来每天修建灌溉水渠y米,技术更新后每天修建米,即1.2y米
则有
解得
经检验,是原方程的解,符合题意
∴乙施工队原来每天修建灌溉水渠90米.
【点拨】本题考查一元一次方程和分式方程的实际应用,应注意分式方程要检验,读懂题意,正确设出未知数,并列出方程,是解题的关键.
37.张老师骑车的速度为千米/小时
【分析】实际应用题的解题步骤“设、列、解、答”,根据问题设未知数,找到题中等量关系张老师先走2小时,结果同时达到列分式方程,求解即可.
【详解】解:设张老师骑车的速度为千米/小时,则汽车速度是千米/小时,
根据题意得:,
解之得,
经检验是分式方程的解,
答:张老师骑车的速度为千米/小时.
【点拨】本题考查分式方程解实际应用题,根据问题设未知数,读懂题意,找到等量关系列出分式方程是解决问题的关键.
38.这款电动汽车平均每公里的充电费为0.2元.
【分析】设这款电动汽车平均每公里的充电费为x元,则燃油车平均每公里的充电费为(x+0.6)元,根据“电动汽车可行驶的总路程是燃油车的4倍”列分式方程,解方程即可求解.
【详解】解:设这款电动汽车平均每公里的充电费为x元.
根据题意,得.
解,得.
经检验,是原方程的根.
答:这款电动汽车平均每公里的充电费为0.2元.
【点拨】本题考查分式方程的应用,分析题意,找到合适的等量关系是解决问题的关键.
39.每个足球的进价是75元,每个篮球的进价是100元
【分析】设每个足球的进价是x元,则每个篮球的进价是(x+25)元,利用数量=总价÷单价,结合用2000元购进篮球的数量是用750元购进足球数量的2倍,即可得出关于x的分式方程,解之经检验后即可得出足球的单价,再将其代入(x+25)中即可求出篮球的单价.
【详解】解:设每个足球的进价是x元,
则每个篮球的进价是(x+25)元,
依题意得:=2×,
解得:x=75,
经检验,x=75是原方程的解,且符合题意,
∴x+25=75+25=100.
答:每个足球的进价是75元,每个篮球的进价是100元.
【点拨】本题考查了分式方程的应用,找准等量关系,正确列出分式方程是解题的关键.
40.小杰平均每分钟清点图书12本,小江平均每分钟清点图书15本
【分析】设小杰平均每分钟清点图书x本,则小江平均每分钟清点图书1.25x本,利用时间=清点图书的总数÷平均每分钟清点图书的数量,结合小江清点完600本图书比小杰清点完540本图书少用了5min,即可得出关于x的分式方程,解之经检验即可得出小杰平均每分钟清点图书数量,再将其代入1.25x中可求出小江平均每分钟清点图书数量.
【详解】解:设小杰平均每分钟清点图书x本,则小江平均每分钟清点图书1.25x本,
依题意得:﹣=5,
解得:x=12,
经检验,x=12是原方程的解,且符合题意,
∴1.25x=1.25×12=15.
答:小杰平均每分钟清点图书12本,小江平均每分钟清点图书15本.
【点拨】本题考查了分式方程的应用,找准等量关系,正确列出分式方程是解题的关键.
41.甲工程队每天改造的道路长度是80米,乙工程队每天改造的道路长度是60米.
【分析】根据题意列出方程求解即可.
【详解】解:设甲工程队每天改造的道路长度是x米,
列方程得:,
解得:x=80.
经检验,x=80是原分式方程的解
80-20=60.
答:甲工程队每天改造的道路长度是80米,乙工程队每天改造的道路长度是60米.
【点拨】此题考查了分式方程应用题的解法,解题的关键是根据题意找到等量关系并列出方程.
42.50
【分析】该商品打折卖出x件,找到等量关系即可.
【详解】解:该商品打折卖出x件
解得x=8
经检验:是原方程的解,且符合题意
∴商品打折前每件元
答:该商品打折前每件50元.
【点拨】此题考查分式方程实际问题中的销售问题,找到等量关系是解题的关键.
43.该景点在设施改造后平均每天用水2吨.
【分析】设该景点在设施改造后平均每天用水x吨,则原来平均每天用水2x吨,列出分式方程,即可求解.
【详解】解:设该景点在设施改造后平均每天用水x吨,则原来平均每天用水2x吨,
由题意得:,解得:x=2,
经检验:x=2是方程的解,且符合题意,
答:该景点在设施改造后平均每天用水2吨.
【点拨】本题主要考查分式方程的实际应用,找出等量关系,列出方程,是解题的关键.
44.(1)第一次每件的进价为50元;(2)两次的总利润为1700元.
【分析】(1)设第一次每件的进价为x元,则第二次进价为(1+20%)x,根据等量关系,列出分式方程,即可求解;
(2)根据总利润=总售价-总成本,列出算式,即可求解.
【详解】解:(1)设第一次每件的进价为x元,则第二次进价为(1+20%)x,
根据题意得:,解得:x=50,
经检验:x=50是方程的解,且符合题意,
答:第一次每件的进价为50元;
(2)(元),
答:两次的总利润为1700元.
【点拨】本题主要考查分式方程的实际应用,找准等量关系,列出分式方程,是解题的关键.
45.(1)小刚跑步的平均速度为150米/分;(2)小刚不能在上课前赶回学校,见解析
【分析】(1)根据题意,列出分式方程即可求得小刚的跑步平均速度;
(2)先求出小刚跑步和骑自行车的时间,加上取作业本和取自行车的时间,与上课时间20分钟作比较即可.
【详解】解:(1)设小刚跑步的平均速度为x米/分,则小刚骑自行车的平均速度为1.6x米/分,
根据题意,得,
解这个方程,得,
经检验,是所列方程的根,
所以小刚跑步的平均速度为150米/分.
(2)由(1)得小刚跑步的平均速度为150米/分,
则小刚跑步所用时间为(分),
骑自行车所用时间为(分),
在家取作业本和取自行车共用了3分,
所以小刚从开始跑步回家到赶回学校需要(分).
因为,
所以小刚不能在上课前赶回学校.
【点拨】本题考查路程问题的分式方程,解题关键是明确题意,列出分式方程求解.
46.2022年A,B两种经济作物分别种植20亩和10亩
【分析】设A,B两种经济作物分别种植x和(30-x)亩,根据B种经济作物亩产值比A种经济作物亩产值多2万元,建立分式方程即可求解.
【详解】解:设2022年A,B两种经济作物分别种植x和(30-x)亩,
由题意可知:A种经济作物亩产值为万元,
B种经济作物亩产值为万元,
由“B种经济作物亩产值比A种经济作物亩产值多2万元”可知:
=+,
解得:或(负值舍去),
经检验,当时原分式方程的分母不为0,
故2022年A,B两种经济作物分别种植20亩和10亩.
【点拨】本题考查了分式方程的应用,关键是要审题仔细,找到题中隐藏的等量关系进而建立方程求解.
47.每千克有机大米的售价为7元.
【分析】设每千克有机大米的售价为x元,则每千克普通大米的售价为(x-2)元,根据“用420元购买的有机大米与用300元购买的普通大米的重量相同”,列出分式方程,即可求解.
【详解】解:设每千克有机大米的售价为x元,则每千克普通大米的售价为(x-2)元,
根据题意得:,解得:x=7,
经检验:x=7是方程的解,且符合题意,
答:每千克有机大米的售价为7元.
【点拨】本题主要考查分式方程的实际应用,找准等量关系,列出分式方程,是解题的关键.
48.(1)甲种消毒液每桶的单价为30元,乙种消毒液每桶的单价为24元;(2)甲种消毒液购买75桶时,所需资金总额最少,最少总金额是4875元.
【分析】(1)根据该单位以零售价分别用900元和720元采购了相同桶数的甲、乙两种消毒液,可以得到相应的分式方程,从而可以得到甲、乙两种消毒剂的零售价,注意分式方程要检验;
(2)设购买甲种消毒液m桶,则购买乙种消毒液(300-m)桶,根据甲种消毒液的桶数不少于乙种消毒液桶数的,即可得出关于m的一元一次不等式,再结合费用总量列出一次函数,根据一次函数性质得出结果.
【详解】解:(1)设甲种消毒液每桶的单价为x元,乙种消毒液每桶的单价为(x-6)元,
依题意,得: ,
解得:x=30,
经检验,x=30是原方程的解,且符合实际意义,则x-6=24.
答:甲种消毒液每桶的单价为30元,乙种消毒液每桶的单价为24元;
(2)设购买甲种消毒液m桶,则购买乙种消毒液(300-m)桶,根据题意得到不等式:
m≥(300-m),解得:m≥75,
∴75≤m≤300,
设总费用为W,根据题意得:
W=20m+15(300-m)=5m+4500,
∵k=5>0,
∴W随m的减小而减小,
∴当m=75时,W有最小值,
∴W=5×75+4500=4875元
∴甲种消毒液购买75桶时,所需资金总额最少,最少总金额是4875元.
【点拨】本题考查一次函数的应用、分式方程的应用、一元一次不等式的应用,解答本题的关键是明确题意,利用一次函数的性质和不等式的性质解答,注意分式方程要检验.
49.(1)这种商品的单价为60元/件;(2)48,50;(3)金额
【分析】(1)根据题意设这种商品的单价为元/件,通过甲乙之间购买的商品数量间的数量关系列分式方程进行求解即可;
(2)利用两次购买总价÷两次购买总数量=平均单价,列式分别求出甲乙两次购买的平均单价即可;
(3)对比(2)中的计算数据总结即可得解.
【详解】(1)设这种商品的单价为元/件,
,解得,经检验是原分式方程的解,
则这种商品的单价为60元/件;
(2)甲,乙两人第二次再去采购该商品时,单价为元/件,
∵甲两次购买总价为元,购买总数量为件,
∴甲两次购买这种商品的平均单价是元/件;
∵乙两次购买总价为元,购买总数量为件,
∴乙两次购买这种商品的平均单价是元/件;
故答案为:48,50;
(3)∵,
∴按照甲两次购买商品的总价相同的情况下更合算,
∴建议按相同金额加油更合算,
故答案为:金额.
【点拨】本题主要考查了分式方程的实际应用,通过题目找准数量关系,利用总价÷数量=单价的基本等量关系式进行求解是解决本题的关键.
50.租用的A种客房每间客房的租金为200元,B种客房每间客房的租金为160元.
【分析】设租用的B种客房每间客房的租金为x元,根据用2000元租到A客房的数量与用1600元租到B客房的数量相等列出方程,解之即可.
【详解】解:设租用的B种客房每间客房的租金为x元,则A种客房每间客房的租金为x+40元,
由题意可得:,
解得:,
经检验:是原方程的解,
160+40=200元,
∴租用的A种客房每间客房的租金为200元,B种客房每间客房的租金为160元.
【点拨】本题考查了分式方程的实际应用,解题的关键是找准等量关系,列出方程.
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
