2023—2024学年浙教版数学七年级下册期末复习压轴题特训课件(41张PPT)
文档属性
| 名称 | 2023—2024学年浙教版数学七年级下册期末复习压轴题特训课件(41张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-12 21:09:56 | ||
图片预览










文档简介
(共41张PPT)
期末压轴题全攻略
考向一 用平行线的判定和性质求角的度数
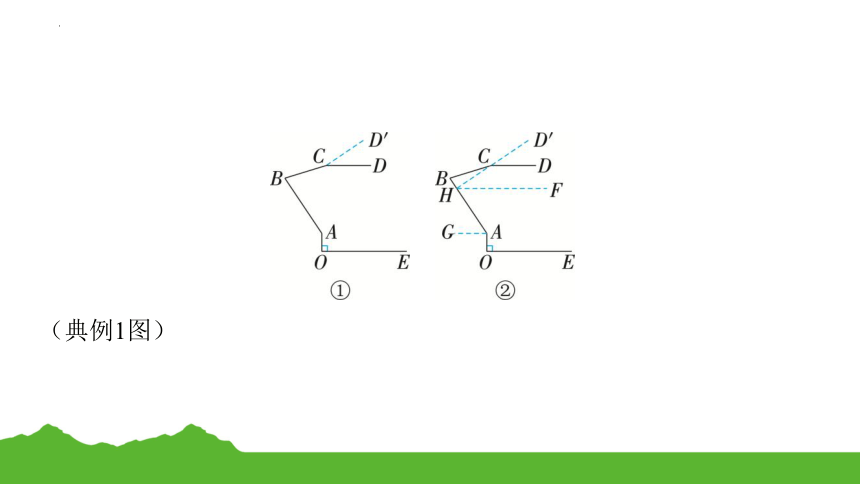
典例1 (2023·宁波慈溪期中)如图①所示为一盏可折叠台灯的平面示意图,OE表示水平桌面,底座AO⊥OE于点O,支架AB,BC为固定支撑杆,∠BAO是∠CBA的2倍,灯体CD可绕点C旋转调节,现把灯体CD从水平位置旋转到CD'的位置,此时,灯体CD'所在的直线恰好垂直于支架AB,且∠BCD-∠DCD'=114°,则∠DCD'的度数为 .
(典例1图)
思路导引 延长D'C交AB于点H,因为两条平行线CD与OE不是被同一条直线所截,在它们之间存在两个拐点H,A,于是考虑分别过点A,H作AG∥OE,FH∥CD. 设∠DCD'=α,则可分别用含α的代数式表示∠HCD,∠BAO,∠CBA,∠BCD的度数.根据∠BCD-∠DCD'=114°列方程求解.
规范解答 如图②,延长D'C交AB于点H,分别过点A,H作AG∥OE,FH∥CD.
设∠DCD'=α,则∠HCD=180°-α.∵ 灯体CD从水平位置旋转,∴ CD∥OE.∵ AG∥OE,FH∥CD,AO⊥OE,∴ AG∥OE∥CD∥FH,∠AOE=90°.∴ ∠CHF=∠DCD'=α,∠GAO=∠AOE=90°,∠HAG=∠AHF.∵ 灯体CD'所在的直线恰好垂直于支架AB,∴ D'C⊥AB.∴ ∠AHC=∠BHC=90°.∴ ∠HAG=∠AHF=∠AHC-∠CHF=90°-α.∴ ∠BAO=∠HAG+∠GAO=90°-α+90°=180°-α.∵ ∠BAO是∠CBA的2倍,∴ ∠CBA=(180°-α)=90°-α.在三角形BHC中,∠BCH=180°-∠BHC-∠CBA=180°-90°-90°+α=α.∴ ∠BCD=∠BCH+∠HCD=α+180°-α=180°-α.∵ ∠BCD-∠DCD'=114°,∴ 180°-α-α=114°,解得α=44°.∴ ∠DCD'= 44°.故填44°.
方法归纳
解两条平行线之间存在拐点问题的方法
当两条平行线不是被同一条直线所截,而是存在拐点时,是不能直接利用平行线的性质进行解答的,这时常常需要通过添设新的平行线,构造出同位角、内错角、同旁内角,为运用平行线的性质创造条件.
现学活用
1. (2023·温州期中)如图,直线AB∥CD,F为直线AB上一点,G为射线BD上一点.若∠CDH=∠HDG,∠EBF=∠GBE,HD交BE于点E,则∠E的度数为( B )
A. 40° B. 45° C. 50° D. 60°
(第1题)
B
考向二 综合运用二元一次方程(组)、整式运算求几何图形的面积
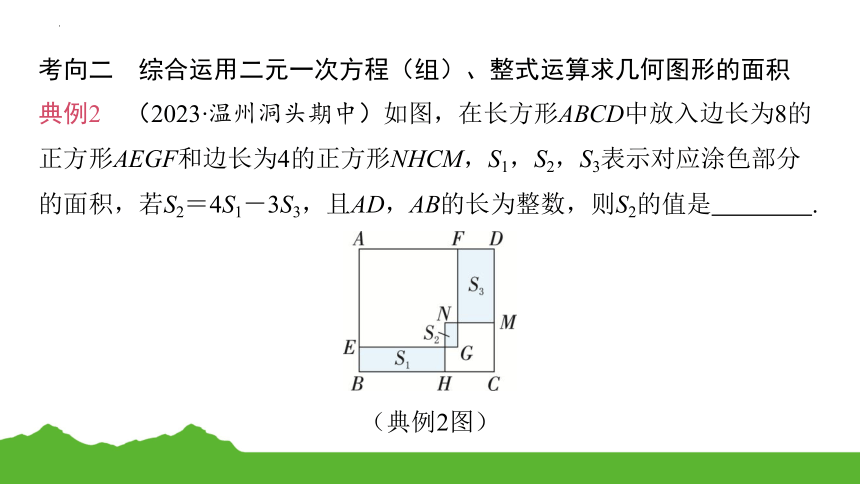
典例2 (2023·温州洞头期中)如图,在长方形ABCD中放入边长为8的正方形AEGF和边长为4的正方形NHCM,S1,S2,S3表示对应涂色部分的面积,若S2=4S1-3S3,且AD,AB的长为整数,则S2的值是 .
(典例2图)
思路导引 延长FG交BC于点Q.设AD=x,AB=y.分别用含x,y的代数式表示S1,S2,S3.根据S2=4S1-3S3,可得关于x,y的方程.根据x,y的取值范围及已知的x,y为整数可求得x,y的值,进而求得S2的值.
规范解答 延长FG交BC于点Q.设AD=x,AB=y,则BC=x,CD=y.∵ 正方形AEGF,NHCM的边长分别为8,4,∴ AE=EG=FG=8,CH=NM=CM=4.∵ BE=AB-AE,BH=BC-CH,∴ BE=y-8,BH=x-4.∴ S1=BE·BH=(y-8)(x-4)=xy-4y-8x+32.同理,可得S3=DF·DM=(x-8)(y-4)=xy-4x-8y+32.设FG与MN交于点P.∵ PG=FG+PQ-FQ=FG+CM-CD,
∴ PG=8+4-y=12-y.∵ NP=HQ=BQ+CH-BC=EG+CH-BC,∴ NP =8+4-x=12-x.∴ S2=PG·NP=(12-y)(12-x)=144-12x-12y+xy.∵ S2=4S1-3S3,∴ 144-12x-12y+xy=4(xy-4y-8x+32)-3(xy-4x-8y+32),化简,得5y-2x=28.∴ x=y-14①.∵ AF<AD=BC<BQ+CH,AE<AB=FQ<FG+PQ,∴ 8<x<12,8<y<12.又∵ x,y均为整数,∴ y=10.把y=10代入①,得x=×10-14=11.∴ ∴ S2=(12-y)·(12-x)=(12-10)×(12-11)=2.故填2.
方法归纳
运用二元一次方程(组)、整式
运算求几何图形的面积的方法
解这类题目时,一般先设题中的两条线段分别为x,y(有的题目设好的除外),然后根据图形中的线段的和差关系,分别用含x,y的代数式表示相关图形的面积所需要的线段的长,接着用含x,y的代数式表示相关图形的面积,最后根据题中的条件得到关于x,y的方程(组),通过解方程求解.若求不出方程的解,则考虑运用整体思想求解.
现学活用
2. (2023·宁波鄞州期中)如图,在长方形ABCD中,AB=3cm,BC=4cm,正方形AEHG,正方形EBKF和正方形NKCM都在它内部,且BK>KC.记AE=xcm,CM=ycm,若x2+y2=10,则长方形PFQD的面积是 cm2 .
cm2
(第2题)
考向三 运用一次方程组解决实际问题
典例3 已知某收费站有编号为①,②,③,④,⑤的五个收费出口,假定各收费出口每小时通过的车流量是不变的,同时开放其中两个收费出口,这两个收费出口1小时一共通过的汽车数量记录如下表.
收费出口编号 ①,② ②,③ ③,④ ④,⑤ ⑤,①
通过的汽车数量(辆) 80 100 70 130 120
下列说法中,错误的是( )
A. ①出口1小时通过的汽车数量最少
B. ⑤出口1小时通过的汽车数量最多
C. ②出口1小时通过的汽车数量是④出口的两倍
D. ①和④出口1小时通过的汽车数量之和等于③出口1小时通过的汽车数量
思路导引 设该收费站①,②,③,④,⑤出口1小时通过的汽车数量分别为a辆,b辆,c辆,d辆,e辆.根据表中的数据列方程组,求出a,b,c,d,e的值,然后分别判断各选项中的说法是否错误.
规范解答 设该收费站①,②,③,④,⑤出口1小时通过的汽车数量分别为a辆,b辆,c辆,d辆,e辆.根据题意,得
解得∴ 该收费站①,②,③,④,⑤出口1小时通过的汽车数量分别为20辆,60辆,40辆,30辆,100辆.∵ 20<30<40<60<100,∴ ①出口1小时通过的汽车数量最少,⑤出口1小时通过的汽车数量最多,故选项A,B的说法正确.∵ 60=2×30,∴ ②出口1小时通过的汽车数量是④出口的两倍,故选项C的说法正确.∵ 20+30>40,∴ ①和④出口1小时通过的汽车数量之和大于③出口1小时通过的汽车数量.故选项D的说法错误.故选D.
现学活用
3. 某农具厂需要用钢管做新型农机具骨架,按设计要求,需要使用粗细相同的长为8分米和25分米的钢管,并要求这些钢管不能是焊接而成的.现钢材市场上这种规格的钢管每根的长为60分米.
(1) 试问:一根60分米长的钢管有哪些裁剪方法呢?请填写下空(余料作废).
方法①:当只裁剪8分米长的钢管时,最多能裁剪出 7 根.
方法②:当先裁剪下1根25分米长的钢管时,余下部分最多能裁剪出8分米长的钢管 4 根.
7
4
方法③:当先裁剪下2根25分米长的钢管时,余下部分最多能裁剪出8分米长的钢管 1 根.
(2) 现分别需要长为25分米和8分米且粗细相同的钢管7根,14根,用(1)中的方法②和方法③各裁剪多少根60分米长的钢管,才能刚好得到所需要的相应数量的钢管?
(3) 现设计要求更新,要用5根60分米长的钢管裁剪出粗细相同的长为5分米的钢管18根,长为8分米和25分米的 钢管若干根,钢管不能焊接,且正好裁 完没有余料,则可裁剪出8分米长的 钢管 20 根和25分米长的钢管 2 根.
1
20
2
解:(2) 设用(1)中的方法②和方法③各裁剪x根和y根60分米长的钢管.∵ 方法②中的1根60分米长的钢管能分别裁剪出25分米、8分米长的钢管1根、4根,∴ x根60分米长的钢管用方法②能分别裁剪出25分米、8分米长的钢管x根、4x根.∵ 方法③中的1根60分米长的钢管能分别裁剪出25分米、8分米长的钢管2根、1根,∴ y根60分米长的钢管用方法③能分别裁剪出25分米、8分米长的钢管2y根、y根.∵ 分别需要长为25分米和8分米且粗细相同的钢管7根,14根,∴ 解得∴ 用(1)中的方法②和方法③各裁剪3根和2根60分米长的钢管.
考向四 与分式运算相关的新定义问题
典例4 (2023·长沙期末)若两个分式M与N的和为常数k,且k为正整数,则称M与N互为“和整分式”,常数k称为“和整值”.如分式M=,N=,M+N==1,则M与N互为“和整分式”,“和整值”k=1.
(1) 已知分式A=,B=,判断A与B是否互为“和整分式”,若不是,请说明理由;若是,请求出“和整值”k.
(2) 已知分式C=,D=,C与D互为“和整分式”,且“和整值”k=3.若x为正整数,分式D的值为正整数t.求:
① G所代表的代数式.
② x的值.
(3) 在(2)的条件下,已知分式P=,Q=,且P+Q=t.若该关于x的方程无解,求实数m的值.
思路导引 (1) 计算A+B,若计算结果为正整数,则A与B互为“和整分式”,那个正整数就是“和整值”k,反之则不是.(2) ① 由C与D互为“和整分式”,且“和整值”k=3,可得关于G的等式,把这个等式当作关于G的 方程,解之可得G所代表的代数式.② 由①可得D,根据分式D的值为正整数且x为正整数可得x的值.(3) 由(2)及P+Q=t,得关于x的方程,根据此方程无解,可求m的值.
规范解答 (1) ∵ A=,B=,∴ A+B=+=+=+==2.
∴ A与B互为“和整分式”,“和整值”k=2.
(2) ① ∵ C=,D=,
∴ C+D=+=.
∵ C与D互为“和整分式”,且“和整值”k=3,∴ =3,即3x2+2x-8+G=3(x-2)(x+2).
∴ G=3(x-2)(x+2)-(3x2+2x-8)=3x2-12-3x2-2x+8=-2x-4.
② 由①,得D===-.
∵ 分式D的值为正整数t,∴ x-2=-1或x-2=-2.∴ x=1或x=0.
又∵ x为正整数,∴ x=1.
(3) 由(2),得t=D=-=2.
∵ P=,Q=,P+Q=t,
∴ +=2.
∴ 3x-5-mx+3=2(x-3).
∴ 整理,得(1-m)x=-4.
若1-m=0,则关于x的方程无解,符合题意.此时1-m=0,解得m=1.
若1-m≠0,则方程(1-m)x=-4有唯一的解.当这个唯一的解是增根x=3时,则原分式方程无解,符合题意. 此时(1-m)×3=-4,解得m=.
综上所述,实数m的值为1或.
现学活用
4. (2023·盐城东台一模)定义:若两个分式的和为n(n为正整数),则称这两个分式互为“N 分式”.
例如:分式与互为“三 分式”.
(1) 分式与 互为“六 分式”.
(2) 若分式与互为“一 分式”(其中a,b为正数),求ab的值.
解:(2) ∵ 分式 与互为“一 分式”,∴ +=1,即=1.∴ a3+2ab+2ab+8b3=a3+2ab+4a2b2+8b3,即4a2b2=2ab.∵ a,b为正数,∴ ab≠0.∴ ab=.
(3) 若正数x,y互为倒数,试说明:分式与互为“五 分式”.
解:(3) ∵ 正数x,y互为倒数,∴ xy=1.∴ x3y3=1.∵ +=+=+=+=+=+====5,
∴ 分式与互为“五 分式”.
1. (2023·淮南凤台期末改编)当x分别取-2 023,-2 022,-2 021,…,-2,-1,0,1,,,…,,,时,计算分式的值,再将所得结果相加,其和为( A )
A. -1 B. 1 C. 0 D.
A
1
2
3
4
5
6
7
2. (2023·金华义乌期中改编)如图,长为ycm,宽为xcm的大长方形被分割为7小块,除涂色A,B外,其余5块是形状、大小完全相同的小长方形,其宽为4cm,有下列说法:① 小长方形的长为(y-12)cm;② 涂色A的宽和涂色B的宽之和为(x-y+4)cm;③ 若x为定值,则涂色A和涂色B的周长和为定值;④ 若x为定值,则涂色A和涂色B的面积和为定值.其中,正确的有( A )
A
A. ①③
B. ②④
C. ①④
D. ①③④
(第2题)
1
2
3
4
5
6
7
3. (2023·温州期中)如图,将正方形ABCD与正方形EFGH叠在一起得到长方形APGQ,四边形PBMG和QGND都是正方形.若长方形APGQ的面积是3,FP=1,HQ=2,连结PC,QC,则四边形APCQ的面积为 .
1
2
3
4
5
6
7
4. 若m2=n+2022,n2=m+2022(m≠n),则代数式m3-2mn+n3的值为 -2022 .
5. (2023·宁波镇海期中)已知m,n,p是正数,且满足++=2,++=,则m+n+p= .
-2022
1
2
3
4
5
6
7
(1) 若∠CFG=76°,则∠BEG的度数是 26° .
(2) 若EG∥A'D',∠A+∠DFE=125°,则∠CFE的度数是 130° .
26°
130°
6. 如图,在四边形纸片ABCD中,AB∥CD,将纸片沿EF折叠,点A,D分别落在点A',D'处,且A'D'经过点B,FD'交BC于点G,连结EG,EG平分∠BEF.
1
2
3
4
5
6
7
7. (2023·郴州永兴期末改编)用如图所示的甲、乙、丙三块木板做一个长、宽、高分别为a厘米,b厘米和10厘米的长方体木箱,其中甲块木板锯成两块刚好能做箱底和一个长侧面,乙块木板刚好能做一个长侧面和一个短侧面,丙块木板刚好能做一个箱盖和剩下的一个短侧面(厚度忽略不计,a>b).
1
2
3
4
5
6
7
(第7题)
(1) 用含a,b的代数式分别表示这三块木板的面积.
解:(1) 甲块木板的面积=S箱底+S长侧面=(ab+10a)平方厘米;乙块木板的面积=S长侧面+S短侧面=(10a+10b)平方厘米;丙块木板的面积= S箱盖+S短侧面=(ab+10b)平方厘米.
1
2
3
4
5
6
7
(2) 若甲块木板的面积比丙块木板的面积大200平方厘米,木箱的体积为15000立方厘米,求乙块木板的面积.
解:(2) 根据题意,得
∴ ∴ (a+b)2=(a-b)2+4ab=202+4×1500=400+6000=6400.∵ a+b>0,∴ a+b=80.∴ 10a+10b=10(a+b)=10×80=800.∴ 乙块木板的面积为800平方厘米.
1
2
3
4
5
6
7
(3) 如果购买一块长为100厘米,宽为(a+b)厘米的长方形木板做这个木箱,木板的利用率为90%,那么方程-=×的解为 x= .
x=
1
2
3
4
5
6
7
期末压轴题全攻略
考向一 用平行线的判定和性质求角的度数
典例1 (2023·宁波慈溪期中)如图①所示为一盏可折叠台灯的平面示意图,OE表示水平桌面,底座AO⊥OE于点O,支架AB,BC为固定支撑杆,∠BAO是∠CBA的2倍,灯体CD可绕点C旋转调节,现把灯体CD从水平位置旋转到CD'的位置,此时,灯体CD'所在的直线恰好垂直于支架AB,且∠BCD-∠DCD'=114°,则∠DCD'的度数为 .
(典例1图)
思路导引 延长D'C交AB于点H,因为两条平行线CD与OE不是被同一条直线所截,在它们之间存在两个拐点H,A,于是考虑分别过点A,H作AG∥OE,FH∥CD. 设∠DCD'=α,则可分别用含α的代数式表示∠HCD,∠BAO,∠CBA,∠BCD的度数.根据∠BCD-∠DCD'=114°列方程求解.
规范解答 如图②,延长D'C交AB于点H,分别过点A,H作AG∥OE,FH∥CD.
设∠DCD'=α,则∠HCD=180°-α.∵ 灯体CD从水平位置旋转,∴ CD∥OE.∵ AG∥OE,FH∥CD,AO⊥OE,∴ AG∥OE∥CD∥FH,∠AOE=90°.∴ ∠CHF=∠DCD'=α,∠GAO=∠AOE=90°,∠HAG=∠AHF.∵ 灯体CD'所在的直线恰好垂直于支架AB,∴ D'C⊥AB.∴ ∠AHC=∠BHC=90°.∴ ∠HAG=∠AHF=∠AHC-∠CHF=90°-α.∴ ∠BAO=∠HAG+∠GAO=90°-α+90°=180°-α.∵ ∠BAO是∠CBA的2倍,∴ ∠CBA=(180°-α)=90°-α.在三角形BHC中,∠BCH=180°-∠BHC-∠CBA=180°-90°-90°+α=α.∴ ∠BCD=∠BCH+∠HCD=α+180°-α=180°-α.∵ ∠BCD-∠DCD'=114°,∴ 180°-α-α=114°,解得α=44°.∴ ∠DCD'= 44°.故填44°.
方法归纳
解两条平行线之间存在拐点问题的方法
当两条平行线不是被同一条直线所截,而是存在拐点时,是不能直接利用平行线的性质进行解答的,这时常常需要通过添设新的平行线,构造出同位角、内错角、同旁内角,为运用平行线的性质创造条件.
现学活用
1. (2023·温州期中)如图,直线AB∥CD,F为直线AB上一点,G为射线BD上一点.若∠CDH=∠HDG,∠EBF=∠GBE,HD交BE于点E,则∠E的度数为( B )
A. 40° B. 45° C. 50° D. 60°
(第1题)
B
考向二 综合运用二元一次方程(组)、整式运算求几何图形的面积
典例2 (2023·温州洞头期中)如图,在长方形ABCD中放入边长为8的正方形AEGF和边长为4的正方形NHCM,S1,S2,S3表示对应涂色部分的面积,若S2=4S1-3S3,且AD,AB的长为整数,则S2的值是 .
(典例2图)
思路导引 延长FG交BC于点Q.设AD=x,AB=y.分别用含x,y的代数式表示S1,S2,S3.根据S2=4S1-3S3,可得关于x,y的方程.根据x,y的取值范围及已知的x,y为整数可求得x,y的值,进而求得S2的值.
规范解答 延长FG交BC于点Q.设AD=x,AB=y,则BC=x,CD=y.∵ 正方形AEGF,NHCM的边长分别为8,4,∴ AE=EG=FG=8,CH=NM=CM=4.∵ BE=AB-AE,BH=BC-CH,∴ BE=y-8,BH=x-4.∴ S1=BE·BH=(y-8)(x-4)=xy-4y-8x+32.同理,可得S3=DF·DM=(x-8)(y-4)=xy-4x-8y+32.设FG与MN交于点P.∵ PG=FG+PQ-FQ=FG+CM-CD,
∴ PG=8+4-y=12-y.∵ NP=HQ=BQ+CH-BC=EG+CH-BC,∴ NP =8+4-x=12-x.∴ S2=PG·NP=(12-y)(12-x)=144-12x-12y+xy.∵ S2=4S1-3S3,∴ 144-12x-12y+xy=4(xy-4y-8x+32)-3(xy-4x-8y+32),化简,得5y-2x=28.∴ x=y-14①.∵ AF<AD=BC<BQ+CH,AE<AB=FQ<FG+PQ,∴ 8<x<12,8<y<12.又∵ x,y均为整数,∴ y=10.把y=10代入①,得x=×10-14=11.∴ ∴ S2=(12-y)·(12-x)=(12-10)×(12-11)=2.故填2.
方法归纳
运用二元一次方程(组)、整式
运算求几何图形的面积的方法
解这类题目时,一般先设题中的两条线段分别为x,y(有的题目设好的除外),然后根据图形中的线段的和差关系,分别用含x,y的代数式表示相关图形的面积所需要的线段的长,接着用含x,y的代数式表示相关图形的面积,最后根据题中的条件得到关于x,y的方程(组),通过解方程求解.若求不出方程的解,则考虑运用整体思想求解.
现学活用
2. (2023·宁波鄞州期中)如图,在长方形ABCD中,AB=3cm,BC=4cm,正方形AEHG,正方形EBKF和正方形NKCM都在它内部,且BK>KC.记AE=xcm,CM=ycm,若x2+y2=10,则长方形PFQD的面积是 cm2 .
cm2
(第2题)
考向三 运用一次方程组解决实际问题
典例3 已知某收费站有编号为①,②,③,④,⑤的五个收费出口,假定各收费出口每小时通过的车流量是不变的,同时开放其中两个收费出口,这两个收费出口1小时一共通过的汽车数量记录如下表.
收费出口编号 ①,② ②,③ ③,④ ④,⑤ ⑤,①
通过的汽车数量(辆) 80 100 70 130 120
下列说法中,错误的是( )
A. ①出口1小时通过的汽车数量最少
B. ⑤出口1小时通过的汽车数量最多
C. ②出口1小时通过的汽车数量是④出口的两倍
D. ①和④出口1小时通过的汽车数量之和等于③出口1小时通过的汽车数量
思路导引 设该收费站①,②,③,④,⑤出口1小时通过的汽车数量分别为a辆,b辆,c辆,d辆,e辆.根据表中的数据列方程组,求出a,b,c,d,e的值,然后分别判断各选项中的说法是否错误.
规范解答 设该收费站①,②,③,④,⑤出口1小时通过的汽车数量分别为a辆,b辆,c辆,d辆,e辆.根据题意,得
解得∴ 该收费站①,②,③,④,⑤出口1小时通过的汽车数量分别为20辆,60辆,40辆,30辆,100辆.∵ 20<30<40<60<100,∴ ①出口1小时通过的汽车数量最少,⑤出口1小时通过的汽车数量最多,故选项A,B的说法正确.∵ 60=2×30,∴ ②出口1小时通过的汽车数量是④出口的两倍,故选项C的说法正确.∵ 20+30>40,∴ ①和④出口1小时通过的汽车数量之和大于③出口1小时通过的汽车数量.故选项D的说法错误.故选D.
现学活用
3. 某农具厂需要用钢管做新型农机具骨架,按设计要求,需要使用粗细相同的长为8分米和25分米的钢管,并要求这些钢管不能是焊接而成的.现钢材市场上这种规格的钢管每根的长为60分米.
(1) 试问:一根60分米长的钢管有哪些裁剪方法呢?请填写下空(余料作废).
方法①:当只裁剪8分米长的钢管时,最多能裁剪出 7 根.
方法②:当先裁剪下1根25分米长的钢管时,余下部分最多能裁剪出8分米长的钢管 4 根.
7
4
方法③:当先裁剪下2根25分米长的钢管时,余下部分最多能裁剪出8分米长的钢管 1 根.
(2) 现分别需要长为25分米和8分米且粗细相同的钢管7根,14根,用(1)中的方法②和方法③各裁剪多少根60分米长的钢管,才能刚好得到所需要的相应数量的钢管?
(3) 现设计要求更新,要用5根60分米长的钢管裁剪出粗细相同的长为5分米的钢管18根,长为8分米和25分米的 钢管若干根,钢管不能焊接,且正好裁 完没有余料,则可裁剪出8分米长的 钢管 20 根和25分米长的钢管 2 根.
1
20
2
解:(2) 设用(1)中的方法②和方法③各裁剪x根和y根60分米长的钢管.∵ 方法②中的1根60分米长的钢管能分别裁剪出25分米、8分米长的钢管1根、4根,∴ x根60分米长的钢管用方法②能分别裁剪出25分米、8分米长的钢管x根、4x根.∵ 方法③中的1根60分米长的钢管能分别裁剪出25分米、8分米长的钢管2根、1根,∴ y根60分米长的钢管用方法③能分别裁剪出25分米、8分米长的钢管2y根、y根.∵ 分别需要长为25分米和8分米且粗细相同的钢管7根,14根,∴ 解得∴ 用(1)中的方法②和方法③各裁剪3根和2根60分米长的钢管.
考向四 与分式运算相关的新定义问题
典例4 (2023·长沙期末)若两个分式M与N的和为常数k,且k为正整数,则称M与N互为“和整分式”,常数k称为“和整值”.如分式M=,N=,M+N==1,则M与N互为“和整分式”,“和整值”k=1.
(1) 已知分式A=,B=,判断A与B是否互为“和整分式”,若不是,请说明理由;若是,请求出“和整值”k.
(2) 已知分式C=,D=,C与D互为“和整分式”,且“和整值”k=3.若x为正整数,分式D的值为正整数t.求:
① G所代表的代数式.
② x的值.
(3) 在(2)的条件下,已知分式P=,Q=,且P+Q=t.若该关于x的方程无解,求实数m的值.
思路导引 (1) 计算A+B,若计算结果为正整数,则A与B互为“和整分式”,那个正整数就是“和整值”k,反之则不是.(2) ① 由C与D互为“和整分式”,且“和整值”k=3,可得关于G的等式,把这个等式当作关于G的 方程,解之可得G所代表的代数式.② 由①可得D,根据分式D的值为正整数且x为正整数可得x的值.(3) 由(2)及P+Q=t,得关于x的方程,根据此方程无解,可求m的值.
规范解答 (1) ∵ A=,B=,∴ A+B=+=+=+==2.
∴ A与B互为“和整分式”,“和整值”k=2.
(2) ① ∵ C=,D=,
∴ C+D=+=.
∵ C与D互为“和整分式”,且“和整值”k=3,∴ =3,即3x2+2x-8+G=3(x-2)(x+2).
∴ G=3(x-2)(x+2)-(3x2+2x-8)=3x2-12-3x2-2x+8=-2x-4.
② 由①,得D===-.
∵ 分式D的值为正整数t,∴ x-2=-1或x-2=-2.∴ x=1或x=0.
又∵ x为正整数,∴ x=1.
(3) 由(2),得t=D=-=2.
∵ P=,Q=,P+Q=t,
∴ +=2.
∴ 3x-5-mx+3=2(x-3).
∴ 整理,得(1-m)x=-4.
若1-m=0,则关于x的方程无解,符合题意.此时1-m=0,解得m=1.
若1-m≠0,则方程(1-m)x=-4有唯一的解.当这个唯一的解是增根x=3时,则原分式方程无解,符合题意. 此时(1-m)×3=-4,解得m=.
综上所述,实数m的值为1或.
现学活用
4. (2023·盐城东台一模)定义:若两个分式的和为n(n为正整数),则称这两个分式互为“N 分式”.
例如:分式与互为“三 分式”.
(1) 分式与 互为“六 分式”.
(2) 若分式与互为“一 分式”(其中a,b为正数),求ab的值.
解:(2) ∵ 分式 与互为“一 分式”,∴ +=1,即=1.∴ a3+2ab+2ab+8b3=a3+2ab+4a2b2+8b3,即4a2b2=2ab.∵ a,b为正数,∴ ab≠0.∴ ab=.
(3) 若正数x,y互为倒数,试说明:分式与互为“五 分式”.
解:(3) ∵ 正数x,y互为倒数,∴ xy=1.∴ x3y3=1.∵ +=+=+=+=+=+====5,
∴ 分式与互为“五 分式”.
1. (2023·淮南凤台期末改编)当x分别取-2 023,-2 022,-2 021,…,-2,-1,0,1,,,…,,,时,计算分式的值,再将所得结果相加,其和为( A )
A. -1 B. 1 C. 0 D.
A
1
2
3
4
5
6
7
2. (2023·金华义乌期中改编)如图,长为ycm,宽为xcm的大长方形被分割为7小块,除涂色A,B外,其余5块是形状、大小完全相同的小长方形,其宽为4cm,有下列说法:① 小长方形的长为(y-12)cm;② 涂色A的宽和涂色B的宽之和为(x-y+4)cm;③ 若x为定值,则涂色A和涂色B的周长和为定值;④ 若x为定值,则涂色A和涂色B的面积和为定值.其中,正确的有( A )
A
A. ①③
B. ②④
C. ①④
D. ①③④
(第2题)
1
2
3
4
5
6
7
3. (2023·温州期中)如图,将正方形ABCD与正方形EFGH叠在一起得到长方形APGQ,四边形PBMG和QGND都是正方形.若长方形APGQ的面积是3,FP=1,HQ=2,连结PC,QC,则四边形APCQ的面积为 .
1
2
3
4
5
6
7
4. 若m2=n+2022,n2=m+2022(m≠n),则代数式m3-2mn+n3的值为 -2022 .
5. (2023·宁波镇海期中)已知m,n,p是正数,且满足++=2,++=,则m+n+p= .
-2022
1
2
3
4
5
6
7
(1) 若∠CFG=76°,则∠BEG的度数是 26° .
(2) 若EG∥A'D',∠A+∠DFE=125°,则∠CFE的度数是 130° .
26°
130°
6. 如图,在四边形纸片ABCD中,AB∥CD,将纸片沿EF折叠,点A,D分别落在点A',D'处,且A'D'经过点B,FD'交BC于点G,连结EG,EG平分∠BEF.
1
2
3
4
5
6
7
7. (2023·郴州永兴期末改编)用如图所示的甲、乙、丙三块木板做一个长、宽、高分别为a厘米,b厘米和10厘米的长方体木箱,其中甲块木板锯成两块刚好能做箱底和一个长侧面,乙块木板刚好能做一个长侧面和一个短侧面,丙块木板刚好能做一个箱盖和剩下的一个短侧面(厚度忽略不计,a>b).
1
2
3
4
5
6
7
(第7题)
(1) 用含a,b的代数式分别表示这三块木板的面积.
解:(1) 甲块木板的面积=S箱底+S长侧面=(ab+10a)平方厘米;乙块木板的面积=S长侧面+S短侧面=(10a+10b)平方厘米;丙块木板的面积= S箱盖+S短侧面=(ab+10b)平方厘米.
1
2
3
4
5
6
7
(2) 若甲块木板的面积比丙块木板的面积大200平方厘米,木箱的体积为15000立方厘米,求乙块木板的面积.
解:(2) 根据题意,得
∴ ∴ (a+b)2=(a-b)2+4ab=202+4×1500=400+6000=6400.∵ a+b>0,∴ a+b=80.∴ 10a+10b=10(a+b)=10×80=800.∴ 乙块木板的面积为800平方厘米.
1
2
3
4
5
6
7
(3) 如果购买一块长为100厘米,宽为(a+b)厘米的长方形木板做这个木箱,木板的利用率为90%,那么方程-=×的解为 x= .
x=
1
2
3
4
5
6
7
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
