浙教版数学七年级下册 3.7 整式的除法 课件(16张PPT)
文档属性
| 名称 | 浙教版数学七年级下册 3.7 整式的除法 课件(16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-23 07:25:09 | ||
图片预览





文档简介
(共16张PPT)
3.7 整式的除法
单击此处添加副标题
创设情境,引入新知
2022年10月16日,中国共产党第二十次全国代表大会开幕。习近平总书记在报告中强调,必须坚持科技是第一生产力,完善科技创新体系。近十年来,我国的研发人员总量居世界首位,一些关键核心技术实现突破。
合作学习,开启新课
近十年来,我国的创新主体不断壮大,研发人员总量连续多年稳居世界
第一位。高科技企业数量从十年前的 家,增至2021年的 家。那么2021年我国现有的高科技企业数量是10年前的几倍呢?
请先按暂停键!思考完成后再按回播放键
系数相除
同底数幂
相除
同底数幂相除法则:
同底数幂相除,底数不变,指数相减
(a≠0,m,n都是正整数)
合作学习,开启新课
近十年来,中国的创新主体不断壮大,研发人员总量连续多年稳居世界
第一位。高新科技企业数量从十年前的 家,增至2021年的 家。那么2021年我国现有的高科技企业数量是10年前的几倍呢?
思考:我们预测下一个十年我国的高科技企业数量将达到 家。
那么下一个十年高科技企业的数量是现在的几倍?
系数相除
同底数幂
相除
分子中单独的字母a保留
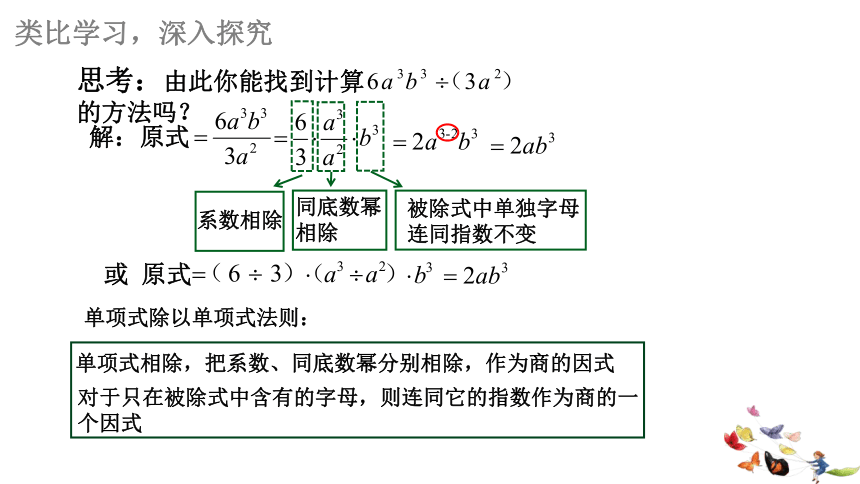
思考:由此你能找到计算 的方法吗?
类比学习,深入探究
解:原式
单项式相除,把系数、同底数幂分别相除,作为商的因式
对于只在被除式中含有的字母,则连同它的指数作为商的一
个因式
系数相除
同底数幂
相除
被除式中单独字母连同指数不变
或 原式
单项式除以单项式法则:
类比学习,深入探究
特殊
一般
研究路径
从特殊的数
到一般的字母
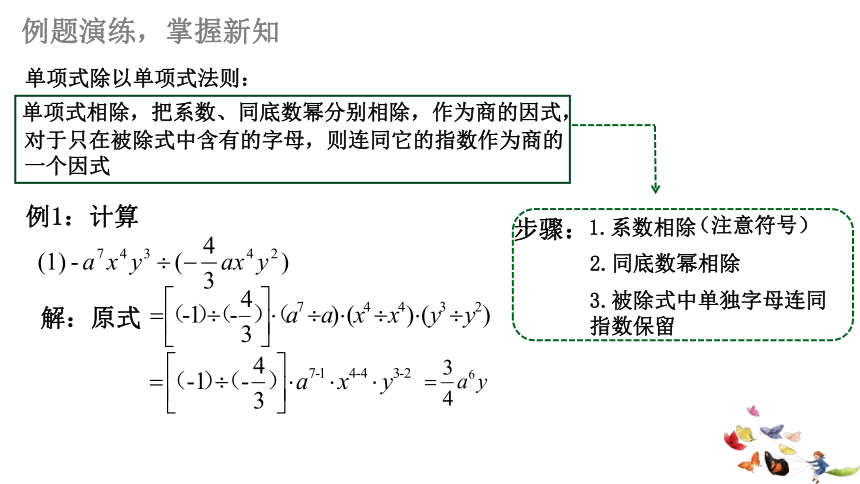
例题演练,掌握新知
例1:计算
解:原式
单项式除以单项式法则:
单项式相除,把系数、同底数幂分别相除,作为商的因式,
对于只在被除式中含有的字母,则连同它的指数作为商的一个因式
1.系数相除
2.同底数幂相除
3.被除式中单独字母连同指数保留
步骤:
(注意符号)
例1:计算
例题演练,掌握新知
解:原式=
先算乘法
再算除法
解:原式
或
注意:同级运算,从左到右计算
1.系数相除
2.同底数幂相除
3.被除式中单独字母连同指数保留
步骤:
(注意符号)
请先按暂停键!思考完成后再按回播放键
注意:对于三个或三个以上的单项式相乘除,法则依然适用
巩固练习,运用新知
练一练:计算
(1)
(2)
(3)
(4)
解:原式=
注意:
注意运算顺序,先乘方,再乘除
( )
请先按暂停键!思考完成后再按回播放键
注意:
被除式中单独字母连同指数保留,不要遗漏
温故新知,探究延伸
多项式除以单项式:
特殊
一般
特殊
计算
解:原式
或 原式
(a+b+c)÷m
你会如何研究多项式除以单项式的运算规律呢?
类比:
研究路径
类比探究,再会新知
一般
由此你能计算以下两个式子吗?
解:原式
解:原式
思考:你能归纳出多项式除以单项式的运算法则吗?
多项式除以单项式,先把这个多项式的每一项除以这个单项式,
(a+b+c)÷m
再把所得的商相加。
+
+
=a÷m b÷m c÷m
多项式除以单项式
单项式除以单项式
转化
(m≠0)
﹌
﹌
﹌
请先按暂停键!思考完成
后再按回播放键
例2:计算
解:原式
典例示范,巩固新知
练一练:计算
请先按暂停键!思考完成后再按回播放键!
解:原式
注意:多项式的每一项都包括它前面的符号
﹌﹌
﹌﹌
+
﹌﹌
﹌﹌﹌
﹌﹌﹌
+
+
巩固练习,运用新知
1.辩一辩:下列计算错在哪里?应如何改正?
注意:
商式的项数,与多项式的项数相同,不要漏项
注意:
多项式的每一项都包括它前面的符号,计算时注意符号
2.填一填:
请先按暂停键!思考完成后再按回播放键
单项式除以单项式法则
知识
技能
多项式除以单项式法则
特殊
一般
研究路径
思想
方法
单项式除以
单项式法则
多项式除以
单项式法则
实数的除法
同底数幂的除法
类比思想
转化思想
特殊到一般
小结新课,梳理新知
1.系数相除
2.同底数幂相除
3.被除式中单独字母连同指数保留
(注意符号)
(a+b+c)÷m
+
+
=a÷m b÷m c÷m
(m≠0)
﹌
﹌
﹌
转化
转化
类比
作业巩固,深化提升
基础作业:请同学们自行下载《作业练习》并完成
拓展作业:请同学们课外查阅资料,研究多项式除以多项式并与同学们分享
结束语
同 学 们 再 见
3.7 整式的除法
单击此处添加副标题
创设情境,引入新知
2022年10月16日,中国共产党第二十次全国代表大会开幕。习近平总书记在报告中强调,必须坚持科技是第一生产力,完善科技创新体系。近十年来,我国的研发人员总量居世界首位,一些关键核心技术实现突破。
合作学习,开启新课
近十年来,我国的创新主体不断壮大,研发人员总量连续多年稳居世界
第一位。高科技企业数量从十年前的 家,增至2021年的 家。那么2021年我国现有的高科技企业数量是10年前的几倍呢?
请先按暂停键!思考完成后再按回播放键
系数相除
同底数幂
相除
同底数幂相除法则:
同底数幂相除,底数不变,指数相减
(a≠0,m,n都是正整数)
合作学习,开启新课
近十年来,中国的创新主体不断壮大,研发人员总量连续多年稳居世界
第一位。高新科技企业数量从十年前的 家,增至2021年的 家。那么2021年我国现有的高科技企业数量是10年前的几倍呢?
思考:我们预测下一个十年我国的高科技企业数量将达到 家。
那么下一个十年高科技企业的数量是现在的几倍?
系数相除
同底数幂
相除
分子中单独的字母a保留
思考:由此你能找到计算 的方法吗?
类比学习,深入探究
解:原式
单项式相除,把系数、同底数幂分别相除,作为商的因式
对于只在被除式中含有的字母,则连同它的指数作为商的一
个因式
系数相除
同底数幂
相除
被除式中单独字母连同指数不变
或 原式
单项式除以单项式法则:
类比学习,深入探究
特殊
一般
研究路径
从特殊的数
到一般的字母
例题演练,掌握新知
例1:计算
解:原式
单项式除以单项式法则:
单项式相除,把系数、同底数幂分别相除,作为商的因式,
对于只在被除式中含有的字母,则连同它的指数作为商的一个因式
1.系数相除
2.同底数幂相除
3.被除式中单独字母连同指数保留
步骤:
(注意符号)
例1:计算
例题演练,掌握新知
解:原式=
先算乘法
再算除法
解:原式
或
注意:同级运算,从左到右计算
1.系数相除
2.同底数幂相除
3.被除式中单独字母连同指数保留
步骤:
(注意符号)
请先按暂停键!思考完成后再按回播放键
注意:对于三个或三个以上的单项式相乘除,法则依然适用
巩固练习,运用新知
练一练:计算
(1)
(2)
(3)
(4)
解:原式=
注意:
注意运算顺序,先乘方,再乘除
( )
请先按暂停键!思考完成后再按回播放键
注意:
被除式中单独字母连同指数保留,不要遗漏
温故新知,探究延伸
多项式除以单项式:
特殊
一般
特殊
计算
解:原式
或 原式
(a+b+c)÷m
你会如何研究多项式除以单项式的运算规律呢?
类比:
研究路径
类比探究,再会新知
一般
由此你能计算以下两个式子吗?
解:原式
解:原式
思考:你能归纳出多项式除以单项式的运算法则吗?
多项式除以单项式,先把这个多项式的每一项除以这个单项式,
(a+b+c)÷m
再把所得的商相加。
+
+
=a÷m b÷m c÷m
多项式除以单项式
单项式除以单项式
转化
(m≠0)
﹌
﹌
﹌
请先按暂停键!思考完成
后再按回播放键
例2:计算
解:原式
典例示范,巩固新知
练一练:计算
请先按暂停键!思考完成后再按回播放键!
解:原式
注意:多项式的每一项都包括它前面的符号
﹌﹌
﹌﹌
+
﹌﹌
﹌﹌﹌
﹌﹌﹌
+
+
巩固练习,运用新知
1.辩一辩:下列计算错在哪里?应如何改正?
注意:
商式的项数,与多项式的项数相同,不要漏项
注意:
多项式的每一项都包括它前面的符号,计算时注意符号
2.填一填:
请先按暂停键!思考完成后再按回播放键
单项式除以单项式法则
知识
技能
多项式除以单项式法则
特殊
一般
研究路径
思想
方法
单项式除以
单项式法则
多项式除以
单项式法则
实数的除法
同底数幂的除法
类比思想
转化思想
特殊到一般
小结新课,梳理新知
1.系数相除
2.同底数幂相除
3.被除式中单独字母连同指数保留
(注意符号)
(a+b+c)÷m
+
+
=a÷m b÷m c÷m
(m≠0)
﹌
﹌
﹌
转化
转化
类比
作业巩固,深化提升
基础作业:请同学们自行下载《作业练习》并完成
拓展作业:请同学们课外查阅资料,研究多项式除以多项式并与同学们分享
结束语
同 学 们 再 见
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
