浙教版七年级数学下册 第一讲 平行线 培优教程 错题整理讲义 (无答案)
文档属性
| 名称 | 浙教版七年级数学下册 第一讲 平行线 培优教程 错题整理讲义 (无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 464.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-07 00:00:00 | ||
图片预览



文档简介
第一讲 平行线
知识梳理
要点诠释
知识点1:同位角、同旁内角、内错角的概念及特征
同位角 同旁内角 内错角
截线EF 同侧 同侧 异侧
被截线AB、CD 同侧 之间 之间
结构特征 F U Z
列举 ∠1与∠5; ∠2与∠6; ∠3与∠7; ∠4与∠8。 ∠3与∠6;∠4与∠5。 ∠3与∠5;∠4与∠6。
知识点2:平行线的定义和平行线公理,及平行线作图步骤
平行线定义:在同一平面内,不相交的两条直线叫作平行线。平行用符号“”表示。
平行线公理:经过直线外一点,有且只有一条直线与这条直线平行。
作图步骤:一放二靠三推四画。
注1:今后遇到线段、射线平行时,特指线段、射线所在的直线平行。
2:在同一平面内,两条直线的关系有平行和相交。
知识点3:平行线的判定和平行线的性质
平行线的判定:判定方法一:平行线的定义;
判定方法二:同位角相等,两直线平行;
判定方法三:内错角相等,两直线平行;
判定方法四:同旁内角互补,两直线平行;
判定方法五:在同一平面内,垂直于同一条直线的两条直线互相平行;
判定方法六:如果两条直线都与第三条直线平行,那么这两条直线也互相平行。
平行线的性质:性质1:两直线平行,同位角相等;
性质2:两直线平行,内错角相等;
性质3:两直线平行,同旁内角互补。
判定定理与性质定理的区别:从角的关系得到结论两直线平行,用平行线判定定理;从平行线得到角相等或互补关系,用平行线性质定理。填理由时,要防止把性质和判定定理相混淆。
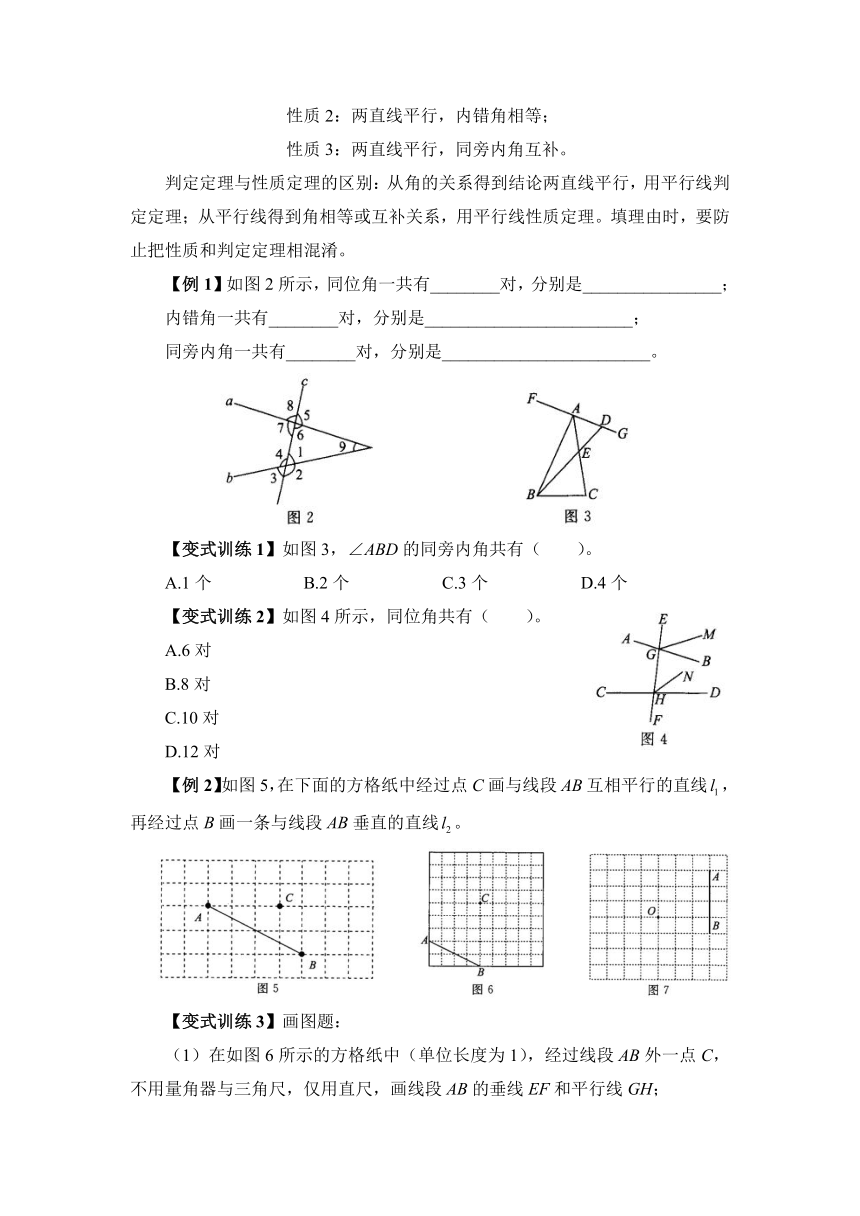
【例1】如图2所示,同位角一共有________对,分别是________________;
内错角一共有________对,分别是________________________;
同旁内角一共有________对,分别是________________________。
【变式训练1】如图3,∠ABD的同旁内角共有( )。
A.1个 B.2个 C.3个 D.4个
【变式训练2】如图4所示,同位角共有( )。
A.6对
B.8对
C.10对
D.12对
【例2】如图5,在下面的方格纸中经过点C画与线段AB互相平行的直线,再经过点B画一条与线段AB垂直的直线。
【变式训练3】画图题:
(1)在如图6所示的方格纸中(单位长度为1),经过线段AB外一点C,不用量角器与三角尺,仅用直尺,画线段AB的垂线EF和平行线GH;
(2)判断EF、GH的位置关系是________;
(3)连接AC和BC,则三角形ABC的面积是________。
【变式训练4】如图7,已知方格纸上点O和线段AB,根据下列要求画图:
(1)画直线OA;
(2)过B点画直线OA的垂线,垂足为D;
(3)取线段AB的中点E,过点E画BD的平行线,交AO于点F。
【例3】设a、b、c为平面上三条不同直线。
(1)若a∥b,b∥c,则a与c的位置关系是________;
(2)若a⊥b,b上c,则a与c的位置关系是________。
【变式训练5】已知直线a∥b,b∥c,c∥d,则a与d的关系是什么?为什么?
【变式训练6】探索与发现:
(1)若直线,,则直线与的位置关系是________,请说明理由;
(2)若直线,,,则直线与的位置关系是________;(直接填结论,不需要证明)
(3)现在有2011条直线,且有,,,…,请你探索直线与的位置关系。
【例4】如图8,已知,,CN是∠BCE的平分线,CM⊥CN,求∠MCD的度数。
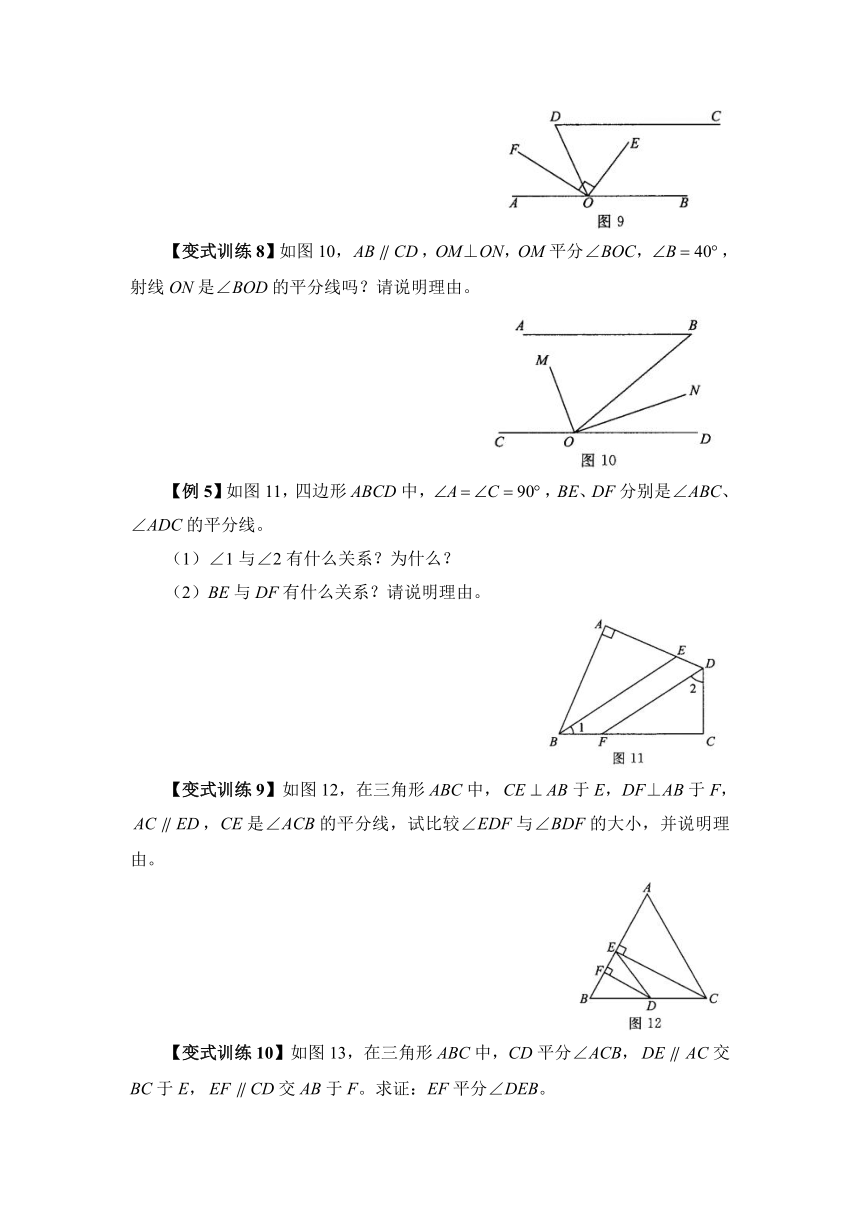
【变式训练7】如图9,已知,OE平分∠BOD,OE⊥OF,,分别求出∠BOE和∠DOF的度数。
【变式训练8】如图10,,OM⊥ON,OM平分∠BOC,,射线ON是∠BOD的平分线吗?请说明理由。
【例5】如图11,四边形ABCD中,,BE、DF分别是∠ABC、∠ADC的平分线。
(1)∠1与∠2有什么关系?为什么?
(2)BE与DF有什么关系?请说明理由。
【变式训练9】如图12,在三角形ABC中,于E,DF⊥AB于F,,CE是∠ACB的平分线,试比较∠EDF与∠BDF的大小,并说明理由。
【变式训练10】如图13,在三角形ABC中,CD平分∠ACB,交BC于E,交AB于F。求证:EF平分∠DEB。
【例6】平面上有10条直线,其中4条直线交于一点,另有4条直线互相平行,这10条直线最多有几个交点?它们最多能把平面分成多少个部分?
【变式训练11】平面内有10条直线,无任何三条交于一点,欲使它们有31个交点,怎样才能办到?
【变式训练12】在同一平面内,若有4条直线,则最多有________个交点;若200条直线中恰好有且只有2m条直线互相平行,则这200条直线最多有________________________个交点。(用含有m的式子表示)
【例7】求证:三角形内角之和等于180°。
【变式训练13】求证:四边形的内角和等于360°。
【变式训练14】证明:五边形内角和等于540°。
【例8】已知,直线,点P为平面上一点,连接AP与CP。
(1)如图①,点P在直线AB、CD之间,当,时,求∠APC;
(2)如图②,点P在直线AB、CD之间,∠BAP与∠DCP的角平分线相交于点K,写出∠AKC与∠APC之间的数量关系,并说明理由;
(3)如图③,点P落在CD外,∠BAP与∠DCP的角平分线相交于点K,∠AKC与∠APC有何数量关系?并说明理由。
【变式训练15】如图①,已知AB∥CD,,。
(1)若,则________;
(2)请探索∠E与∠F之间满足的数量关系并说明理由;
(3)如图②,已知EP平分∠BEF,FG平分∠EFD,反向延长FG交EP于点P,求∠P的度数。
【变式训练16】如图16所示,已知AB∥CD,BE平分∠ABD,DE平分∠BDC。(∠ABD的度数大于90°,小于120°)
(1)求证:;
(2)若点F为射线BE上一点,,∠ABF的角平分线BG与∠CDF的角平分线DG交于点G,试用含的式子表示∠BGD的大小;
(3)延长BE交CD于点H,点F为线段BH上一动点,∠ABF邻补角的角平分线与∠CDF邻补角的角平分线DG交于点G,探究∠BGD与∠BFD之间的数量关系,请直接写出结论:______________________________。(题中所有的角都是大于0°、小于180°的角)
【例9】如图17,已知,,,求证:。
【变式训练17】(1)如图①,已知,若,,求证:;
(2)如图②,若,,,求证:;
(3)若,,,则与的数量关系是_________(用含有的代数式表示,不证明)
【变式训练18】已知直线,为直线AB、CD外的一点,连接AE、EC。
(1)E在直线AB的上方(如图①),求证:;
(2),(如图②),求证:,
(3)若E在直线,CD之间,在(2)条件下(如图③),且∠AFC比的倍少,则的度数为________。(不用写出解答过程)
【例10】(1)如图①,若AB∥CD,则,你能说明理由吗?
(2)反之,在图①中,若,直线AB与CD有什么位置关系?
(3)若将点E移至图②的位置,此时∠B、∠D、∠E之间有什么关系?
(4)在图③中,,与之间有何关系?
【变式训练19】探究:
(1)如图a,若AB∥CD,则,你能说明为什么吗?
(2)反之,若,直线AB与CD有什么位置关系?请证明;
(3)若将点E移至图b所示位置,此时∠B、∠D、∠E之间有什么关系?请证明;
(4)若将E点移至图c所示位置,情况又如何?
(5)在图d中,AB∥CD,与又有何关系?
【变式训练20】已知:。
(1)在图(3)中,之间有什么数量关系?请直接写出结论;
(2)若将点移至图(4)位値,之间有什么数量关系?请直接写出结论。
夯实中考
一、选择题
1.如图23,,,则∠4的度数是( )。
A.74° B.76° C.84° D.86°
2.如图24,直线,AE⊥CE于点E,若,则∠ECD的度数是( )。
A.120° B.100° C.150° D.160°
3.如图25,工人师傅用角尺画出工件边缘AB的垂线a和b,得到a∥b。理由是( )。
A.连接直线外一点与直线上各点的所有线段中,垂线段最短
B.在同一平面内,垂直于同一条直线的两条直线互相平行
C.在同一平面内,过一点有一条而且仅有一条直线垂直于已知直线
D.经过直线外一点,有且只有一条直线与这条直线平行
4.如图26,AC与BD交于点O,AB∥CD,,,则∠C的度数为( )。
A.45° B.55° C.60° D.75°
二、填空题
5.已知直线a∥b,将一块含30°角的直角三角板ABC按如图27所示方式放置(),并且顶点A、C分别落在直线a、b上,若,则∠2的度数是________。
6.如图28,m∥n,,,则________
7.如图29,直线a∥b,,,则________
8.将一副三角板如图30所示放置,使点A落在DE上,若BC∥DE,则∠AFC的度数为________。
三、解答题
9.如图31,直线EF分别与直线AB、CD交于点E、F。EM平分∠BEF,FN平分∠CFE,且EM∥FN。
求证:AB∥CD。
10.如图32,直线EF∥GH,点A在EF上,AC交GH于点B,若,,点D在GH上,求∠BDC的度数。
11.如图甲,E是直线AB、CD内部一点,AB∥CD,连接EA、ED。
(1)探究猜想:
①若,,则∠AED等于多少度?
②若,,则∠AED等于多少度?
③猜想图甲中∠AED、∠EAB、∠EDC的关系并证明你的结论。
(2)拓展应用:
如图乙,射线FE与矩形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的4个区域(不含边界,其中区域③、④位于直线AB上方,P是位于以上四个区域上的点)。
猜想:∠PEB、∠PFC、∠EPF的关系(不要求证明)。
知识梳理
要点诠释
知识点1:同位角、同旁内角、内错角的概念及特征
同位角 同旁内角 内错角
截线EF 同侧 同侧 异侧
被截线AB、CD 同侧 之间 之间
结构特征 F U Z
列举 ∠1与∠5; ∠2与∠6; ∠3与∠7; ∠4与∠8。 ∠3与∠6;∠4与∠5。 ∠3与∠5;∠4与∠6。
知识点2:平行线的定义和平行线公理,及平行线作图步骤
平行线定义:在同一平面内,不相交的两条直线叫作平行线。平行用符号“”表示。
平行线公理:经过直线外一点,有且只有一条直线与这条直线平行。
作图步骤:一放二靠三推四画。
注1:今后遇到线段、射线平行时,特指线段、射线所在的直线平行。
2:在同一平面内,两条直线的关系有平行和相交。
知识点3:平行线的判定和平行线的性质
平行线的判定:判定方法一:平行线的定义;
判定方法二:同位角相等,两直线平行;
判定方法三:内错角相等,两直线平行;
判定方法四:同旁内角互补,两直线平行;
判定方法五:在同一平面内,垂直于同一条直线的两条直线互相平行;
判定方法六:如果两条直线都与第三条直线平行,那么这两条直线也互相平行。
平行线的性质:性质1:两直线平行,同位角相等;
性质2:两直线平行,内错角相等;
性质3:两直线平行,同旁内角互补。
判定定理与性质定理的区别:从角的关系得到结论两直线平行,用平行线判定定理;从平行线得到角相等或互补关系,用平行线性质定理。填理由时,要防止把性质和判定定理相混淆。
【例1】如图2所示,同位角一共有________对,分别是________________;
内错角一共有________对,分别是________________________;
同旁内角一共有________对,分别是________________________。
【变式训练1】如图3,∠ABD的同旁内角共有( )。
A.1个 B.2个 C.3个 D.4个
【变式训练2】如图4所示,同位角共有( )。
A.6对
B.8对
C.10对
D.12对
【例2】如图5,在下面的方格纸中经过点C画与线段AB互相平行的直线,再经过点B画一条与线段AB垂直的直线。
【变式训练3】画图题:
(1)在如图6所示的方格纸中(单位长度为1),经过线段AB外一点C,不用量角器与三角尺,仅用直尺,画线段AB的垂线EF和平行线GH;
(2)判断EF、GH的位置关系是________;
(3)连接AC和BC,则三角形ABC的面积是________。
【变式训练4】如图7,已知方格纸上点O和线段AB,根据下列要求画图:
(1)画直线OA;
(2)过B点画直线OA的垂线,垂足为D;
(3)取线段AB的中点E,过点E画BD的平行线,交AO于点F。
【例3】设a、b、c为平面上三条不同直线。
(1)若a∥b,b∥c,则a与c的位置关系是________;
(2)若a⊥b,b上c,则a与c的位置关系是________。
【变式训练5】已知直线a∥b,b∥c,c∥d,则a与d的关系是什么?为什么?
【变式训练6】探索与发现:
(1)若直线,,则直线与的位置关系是________,请说明理由;
(2)若直线,,,则直线与的位置关系是________;(直接填结论,不需要证明)
(3)现在有2011条直线,且有,,,…,请你探索直线与的位置关系。
【例4】如图8,已知,,CN是∠BCE的平分线,CM⊥CN,求∠MCD的度数。
【变式训练7】如图9,已知,OE平分∠BOD,OE⊥OF,,分别求出∠BOE和∠DOF的度数。
【变式训练8】如图10,,OM⊥ON,OM平分∠BOC,,射线ON是∠BOD的平分线吗?请说明理由。
【例5】如图11,四边形ABCD中,,BE、DF分别是∠ABC、∠ADC的平分线。
(1)∠1与∠2有什么关系?为什么?
(2)BE与DF有什么关系?请说明理由。
【变式训练9】如图12,在三角形ABC中,于E,DF⊥AB于F,,CE是∠ACB的平分线,试比较∠EDF与∠BDF的大小,并说明理由。
【变式训练10】如图13,在三角形ABC中,CD平分∠ACB,交BC于E,交AB于F。求证:EF平分∠DEB。
【例6】平面上有10条直线,其中4条直线交于一点,另有4条直线互相平行,这10条直线最多有几个交点?它们最多能把平面分成多少个部分?
【变式训练11】平面内有10条直线,无任何三条交于一点,欲使它们有31个交点,怎样才能办到?
【变式训练12】在同一平面内,若有4条直线,则最多有________个交点;若200条直线中恰好有且只有2m条直线互相平行,则这200条直线最多有________________________个交点。(用含有m的式子表示)
【例7】求证:三角形内角之和等于180°。
【变式训练13】求证:四边形的内角和等于360°。
【变式训练14】证明:五边形内角和等于540°。
【例8】已知,直线,点P为平面上一点,连接AP与CP。
(1)如图①,点P在直线AB、CD之间,当,时,求∠APC;
(2)如图②,点P在直线AB、CD之间,∠BAP与∠DCP的角平分线相交于点K,写出∠AKC与∠APC之间的数量关系,并说明理由;
(3)如图③,点P落在CD外,∠BAP与∠DCP的角平分线相交于点K,∠AKC与∠APC有何数量关系?并说明理由。
【变式训练15】如图①,已知AB∥CD,,。
(1)若,则________;
(2)请探索∠E与∠F之间满足的数量关系并说明理由;
(3)如图②,已知EP平分∠BEF,FG平分∠EFD,反向延长FG交EP于点P,求∠P的度数。
【变式训练16】如图16所示,已知AB∥CD,BE平分∠ABD,DE平分∠BDC。(∠ABD的度数大于90°,小于120°)
(1)求证:;
(2)若点F为射线BE上一点,,∠ABF的角平分线BG与∠CDF的角平分线DG交于点G,试用含的式子表示∠BGD的大小;
(3)延长BE交CD于点H,点F为线段BH上一动点,∠ABF邻补角的角平分线与∠CDF邻补角的角平分线DG交于点G,探究∠BGD与∠BFD之间的数量关系,请直接写出结论:______________________________。(题中所有的角都是大于0°、小于180°的角)
【例9】如图17,已知,,,求证:。
【变式训练17】(1)如图①,已知,若,,求证:;
(2)如图②,若,,,求证:;
(3)若,,,则与的数量关系是_________(用含有的代数式表示,不证明)
【变式训练18】已知直线,为直线AB、CD外的一点,连接AE、EC。
(1)E在直线AB的上方(如图①),求证:;
(2),(如图②),求证:,
(3)若E在直线,CD之间,在(2)条件下(如图③),且∠AFC比的倍少,则的度数为________。(不用写出解答过程)
【例10】(1)如图①,若AB∥CD,则,你能说明理由吗?
(2)反之,在图①中,若,直线AB与CD有什么位置关系?
(3)若将点E移至图②的位置,此时∠B、∠D、∠E之间有什么关系?
(4)在图③中,,与之间有何关系?
【变式训练19】探究:
(1)如图a,若AB∥CD,则,你能说明为什么吗?
(2)反之,若,直线AB与CD有什么位置关系?请证明;
(3)若将点E移至图b所示位置,此时∠B、∠D、∠E之间有什么关系?请证明;
(4)若将E点移至图c所示位置,情况又如何?
(5)在图d中,AB∥CD,与又有何关系?
【变式训练20】已知:。
(1)在图(3)中,之间有什么数量关系?请直接写出结论;
(2)若将点移至图(4)位値,之间有什么数量关系?请直接写出结论。
夯实中考
一、选择题
1.如图23,,,则∠4的度数是( )。
A.74° B.76° C.84° D.86°
2.如图24,直线,AE⊥CE于点E,若,则∠ECD的度数是( )。
A.120° B.100° C.150° D.160°
3.如图25,工人师傅用角尺画出工件边缘AB的垂线a和b,得到a∥b。理由是( )。
A.连接直线外一点与直线上各点的所有线段中,垂线段最短
B.在同一平面内,垂直于同一条直线的两条直线互相平行
C.在同一平面内,过一点有一条而且仅有一条直线垂直于已知直线
D.经过直线外一点,有且只有一条直线与这条直线平行
4.如图26,AC与BD交于点O,AB∥CD,,,则∠C的度数为( )。
A.45° B.55° C.60° D.75°
二、填空题
5.已知直线a∥b,将一块含30°角的直角三角板ABC按如图27所示方式放置(),并且顶点A、C分别落在直线a、b上,若,则∠2的度数是________。
6.如图28,m∥n,,,则________
7.如图29,直线a∥b,,,则________
8.将一副三角板如图30所示放置,使点A落在DE上,若BC∥DE,则∠AFC的度数为________。
三、解答题
9.如图31,直线EF分别与直线AB、CD交于点E、F。EM平分∠BEF,FN平分∠CFE,且EM∥FN。
求证:AB∥CD。
10.如图32,直线EF∥GH,点A在EF上,AC交GH于点B,若,,点D在GH上,求∠BDC的度数。
11.如图甲,E是直线AB、CD内部一点,AB∥CD,连接EA、ED。
(1)探究猜想:
①若,,则∠AED等于多少度?
②若,,则∠AED等于多少度?
③猜想图甲中∠AED、∠EAB、∠EDC的关系并证明你的结论。
(2)拓展应用:
如图乙,射线FE与矩形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的4个区域(不含边界,其中区域③、④位于直线AB上方,P是位于以上四个区域上的点)。
猜想:∠PEB、∠PFC、∠EPF的关系(不要求证明)。
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
