15-16学年七年级数学(浙教版)下册教学课件:第1章 平行线小结(共18张PPT)
文档属性
| 名称 | 15-16学年七年级数学(浙教版)下册教学课件:第1章 平行线小结(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 928.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-02-29 15:10:12 | ||
图片预览




文档简介
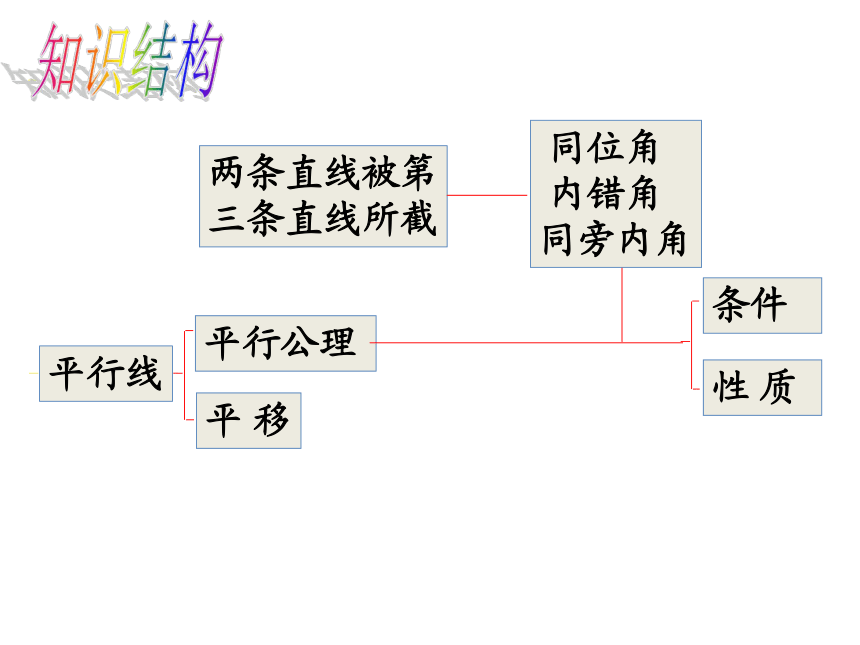
课件18张PPT。义务教育教科书(浙教)七年级数学下册第1章 平行线小 结平行线两条直线被第
三条直线所截 同位角
内错角
同旁内角平行公理 平 移条件性 质知识结构1 三线八角:
2 平行线的判定方法:(1)同位角相等,两直线平行
(2)内错角相等,两直线平行
(3)同旁内角互补,两直线平行
平行或(垂直)于同一直线的两条直线互相平行同位角 内错角 同旁内角过直线外的一点有且只有一条直线与已知直线
平行。
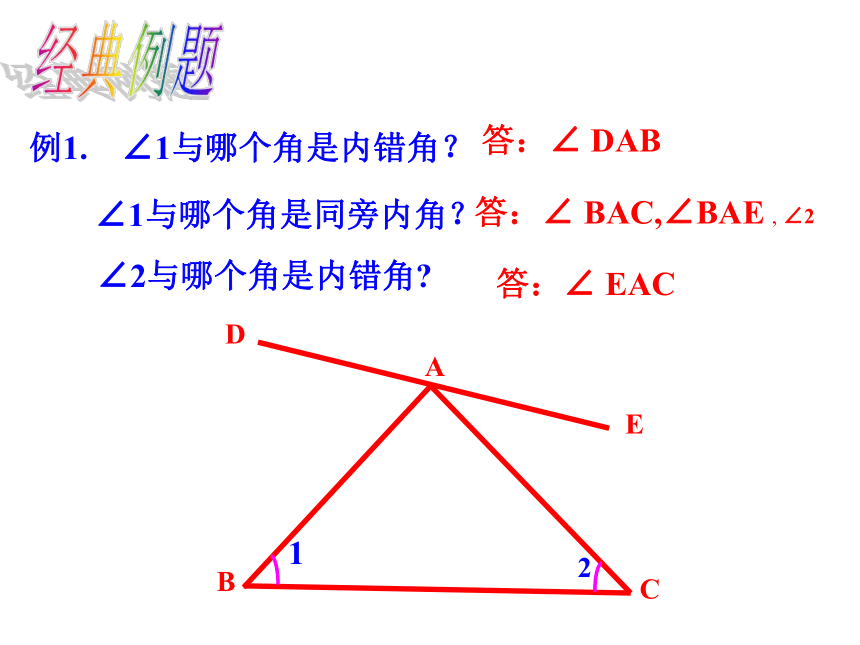
3.平行性质:知识要点例1. ∠1与哪个角是内错角?
ACBDE12答:∠ EAC答:∠ DAB答:∠ BAC,∠BAE , ∠2 ∠1与哪个角是同旁内角?
∠2与哪个角是内错角?经典例题两直线平行,同位角相等
两直线平行,内错角相等
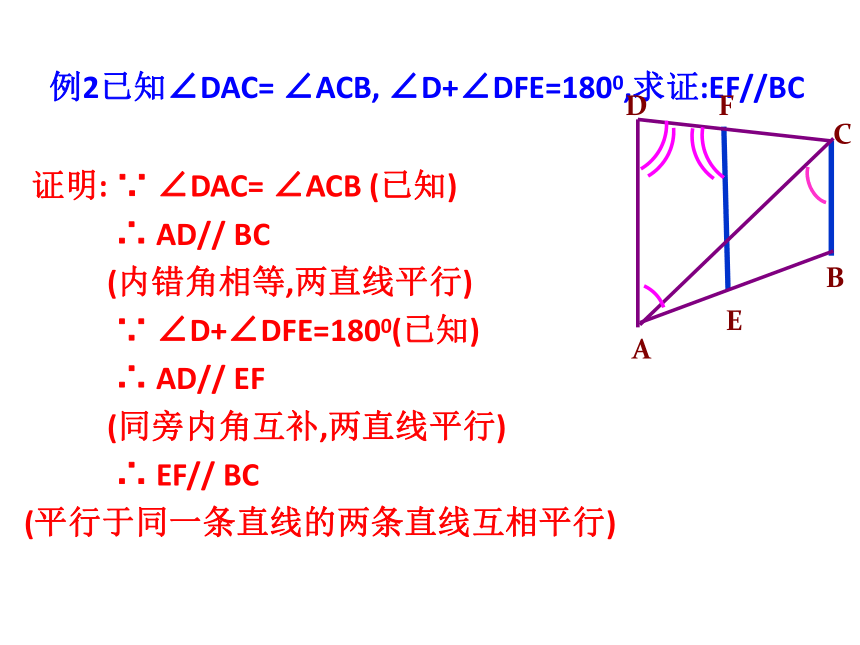
两直线平行,同旁内角互补4 平行线的性质:5 点到直线的距离6 平行线的距离直线外一点到这条直线的垂线段的长度叫做点到直线的距离。夹在两条平行线间的垂线段的长度。例2已知∠DAC= ∠ACB, ∠D+∠DFE=1800,求证:EF//BC 证明: ∵ ∠DAC= ∠ACB (已知)
∴ AD// BC
(内错角相等,两直线平行)
∵ ∠D+∠DFE=1800(已知)
∴ AD// EF
(同旁内角互补,两直线平行)
∴ EF// BC
(平行于同一条直线的两条直线互相平行)
ABCDEF例3. 如图 已知:∠1+∠2=180°, 求证:AB∥CD。 证明:由:∠1+∠2=180°(已知),
∠1=∠3(对顶角相等).
∠2=∠4(对顶角相等) 根据:等量代换 得:∠3+∠4=180°.
根据:同旁内角互补,两直线平行
得:AB//CD .例4已知 EF⊥AB,CD⊥AB,∠EFB=∠GDC,求证:∠AGD=∠ACB。
证明: ∵ EF⊥AB,CD⊥AB (已知)
∴ AD∥BC
(垂直于同一条直线的两条直线互相平行)
∴ ∠EFB= ∠DCB
(两直线平行,同位角相等)
∵ ∠EFB=∠GDC (已知)
∴ ∠DCB=∠GDC (等量代换)
∴ DG∥BC (内错角相等,两直线平行)
∴ ∠AGD=∠ACB
(两直线平行,同位角相等)
7.平移:
平移的定义: 把一个图形整体沿某一方向移动,会得到
一个新图形,这样的图形运动,叫做平移。
平移的特征: (1)平移不改变图形的形状和大小。
(2)新图形中的每一点,都是由原图形中的某一点移动后得到
的,这两个点是对应点,对应点连结而成的线段平行且相等。
决定平移的因素是平移的方向和距离。
经过平移,图形上的每一点都沿同一方向移动相同的距离。
经过平移,对应角相等;对应线段平行且相等;对应点所连的线
段平行且相等。例5.在以下生活现象中,不是平移现象的是站在运动着的电梯上的人
左右推动的推拉窗扇
小李荡秋千运动
的躺在火车上睡觉的旅客分析: A、B、D属平移,在一个位置取两点连成一条线
,在另一个位置再观察这条线段,发现是平行的,而C
同样取两点连成一条线段,运动到另一位置时,可能已
不平行解: 选C例6.如图所示,△ABC平移到△A′B′C′的位置,则点A的
对应点是______,点B的对应点是______,点C的对应点是____
。线段AB的对应线段是___________,线段BC的对应线段是
_________,线段AC的对应线段是___________。∠BAC的对应
角是__________,∠ABC的对应角是____________,∠ACB的
对应角是___________。△ABC的平移方向是________________
___________________________,平移距离是_______________
_____________________________。ABCA′B′C′A′B′C′沿着射线AA′
(或BB′,或CC′)的方向线段AA′的长(或线段BB′的长或线段CC′的长1.(1)能由△AOB平移而得的图形是哪个?(2)如图,AB ∥CD,
若∠ABE=120o ∠DCE=35o,则 ∠ BEC =___随堂练习2.如图,不能判别AB∥CD的条件是( )
A. ∠B+ ∠BCD=180° B. ∠1= ∠2
C. ∠3= ∠4 D. ∠B= ∠5B3. 如图,已知∠1=∠3,AC平分∠DAB,你能推断哪两条直线平行?请说明理由.解: 可以推断出AB ∥ CD .理由如下:
∵ AC平分∠DAB,
∴ ∠1=∠2
∵ ∠1=∠3,
∴ ∠2=∠3,
∴ AB ∥ CD5. 如图,AD⊥BC于D,EG⊥BC于G,∠E=∠3
试说明:AD平分∠BAC
答:因为AD⊥BC,EG⊥BC
所以AD∥EG( )
所以∠1=∠E( )
∠2=∠3( )
又因为∠3=∠E ( )
所以∠1=∠2 ( )
所以AD平分∠BAC( )1垂直于同一直线的两条直线互相平行两直线平行,同位角相等两直线平行,内错角相等已知角平分线定义等量代换随堂练习
三条直线所截 同位角
内错角
同旁内角平行公理 平 移条件性 质知识结构1 三线八角:
2 平行线的判定方法:(1)同位角相等,两直线平行
(2)内错角相等,两直线平行
(3)同旁内角互补,两直线平行
平行或(垂直)于同一直线的两条直线互相平行同位角 内错角 同旁内角过直线外的一点有且只有一条直线与已知直线
平行。
3.平行性质:知识要点例1. ∠1与哪个角是内错角?
ACBDE12答:∠ EAC答:∠ DAB答:∠ BAC,∠BAE , ∠2 ∠1与哪个角是同旁内角?
∠2与哪个角是内错角?经典例题两直线平行,同位角相等
两直线平行,内错角相等
两直线平行,同旁内角互补4 平行线的性质:5 点到直线的距离6 平行线的距离直线外一点到这条直线的垂线段的长度叫做点到直线的距离。夹在两条平行线间的垂线段的长度。例2已知∠DAC= ∠ACB, ∠D+∠DFE=1800,求证:EF//BC 证明: ∵ ∠DAC= ∠ACB (已知)
∴ AD// BC
(内错角相等,两直线平行)
∵ ∠D+∠DFE=1800(已知)
∴ AD// EF
(同旁内角互补,两直线平行)
∴ EF// BC
(平行于同一条直线的两条直线互相平行)
ABCDEF例3. 如图 已知:∠1+∠2=180°, 求证:AB∥CD。 证明:由:∠1+∠2=180°(已知),
∠1=∠3(对顶角相等).
∠2=∠4(对顶角相等) 根据:等量代换 得:∠3+∠4=180°.
根据:同旁内角互补,两直线平行
得:AB//CD .例4已知 EF⊥AB,CD⊥AB,∠EFB=∠GDC,求证:∠AGD=∠ACB。
证明: ∵ EF⊥AB,CD⊥AB (已知)
∴ AD∥BC
(垂直于同一条直线的两条直线互相平行)
∴ ∠EFB= ∠DCB
(两直线平行,同位角相等)
∵ ∠EFB=∠GDC (已知)
∴ ∠DCB=∠GDC (等量代换)
∴ DG∥BC (内错角相等,两直线平行)
∴ ∠AGD=∠ACB
(两直线平行,同位角相等)
7.平移:
平移的定义: 把一个图形整体沿某一方向移动,会得到
一个新图形,这样的图形运动,叫做平移。
平移的特征: (1)平移不改变图形的形状和大小。
(2)新图形中的每一点,都是由原图形中的某一点移动后得到
的,这两个点是对应点,对应点连结而成的线段平行且相等。
决定平移的因素是平移的方向和距离。
经过平移,图形上的每一点都沿同一方向移动相同的距离。
经过平移,对应角相等;对应线段平行且相等;对应点所连的线
段平行且相等。例5.在以下生活现象中,不是平移现象的是站在运动着的电梯上的人
左右推动的推拉窗扇
小李荡秋千运动
的躺在火车上睡觉的旅客分析: A、B、D属平移,在一个位置取两点连成一条线
,在另一个位置再观察这条线段,发现是平行的,而C
同样取两点连成一条线段,运动到另一位置时,可能已
不平行解: 选C例6.如图所示,△ABC平移到△A′B′C′的位置,则点A的
对应点是______,点B的对应点是______,点C的对应点是____
。线段AB的对应线段是___________,线段BC的对应线段是
_________,线段AC的对应线段是___________。∠BAC的对应
角是__________,∠ABC的对应角是____________,∠ACB的
对应角是___________。△ABC的平移方向是________________
___________________________,平移距离是_______________
_____________________________。ABCA′B′C′A′B′C′沿着射线AA′
(或BB′,或CC′)的方向线段AA′的长(或线段BB′的长或线段CC′的长1.(1)能由△AOB平移而得的图形是哪个?(2)如图,AB ∥CD,
若∠ABE=120o ∠DCE=35o,则 ∠ BEC =___随堂练习2.如图,不能判别AB∥CD的条件是( )
A. ∠B+ ∠BCD=180° B. ∠1= ∠2
C. ∠3= ∠4 D. ∠B= ∠5B3. 如图,已知∠1=∠3,AC平分∠DAB,你能推断哪两条直线平行?请说明理由.解: 可以推断出AB ∥ CD .理由如下:
∵ AC平分∠DAB,
∴ ∠1=∠2
∵ ∠1=∠3,
∴ ∠2=∠3,
∴ AB ∥ CD5. 如图,AD⊥BC于D,EG⊥BC于G,∠E=∠3
试说明:AD平分∠BAC
答:因为AD⊥BC,EG⊥BC
所以AD∥EG( )
所以∠1=∠E( )
∠2=∠3( )
又因为∠3=∠E ( )
所以∠1=∠2 ( )
所以AD平分∠BAC( )1垂直于同一直线的两条直线互相平行两直线平行,同位角相等两直线平行,内错角相等已知角平分线定义等量代换随堂练习
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
