1.4 平行线的性质课件(第二课时)

课件22张PPT。1.4平行线的性质（二）教学目标：
1. 经历平行线的性质“两直线平行，内错角相等”“两直线平行，同旁内角互补”的发现过程.
2． 掌握“两直线平行，内错角相等”“两直线平行，同旁内角互补”这两个平行线的性质．
3． 会用平行线的性质“两直线平行， 内错角相等”“两直线平行， 同旁内角互补” 进行简单的推理和判断．
●本节教学的重点是平行线的性质:“两直线平行，内错角相等”“两直线平行，同旁内角互补” .
●例 ４ 的推理过程包括了平行线的性质和判定方法两方面的应用，是本节教学的难点．
合作学习 如图，直线AB//CD，并被直线EF所截.∠2与∠3相等吗?∠3与∠4的和是多少度?
建议从以下几方面思考:
⑴回顾我们已经知道的平行线的性质,由此能得出图中哪一对角相等?
⑵∠3与∠1有什么关系?∠4与∠2呢?
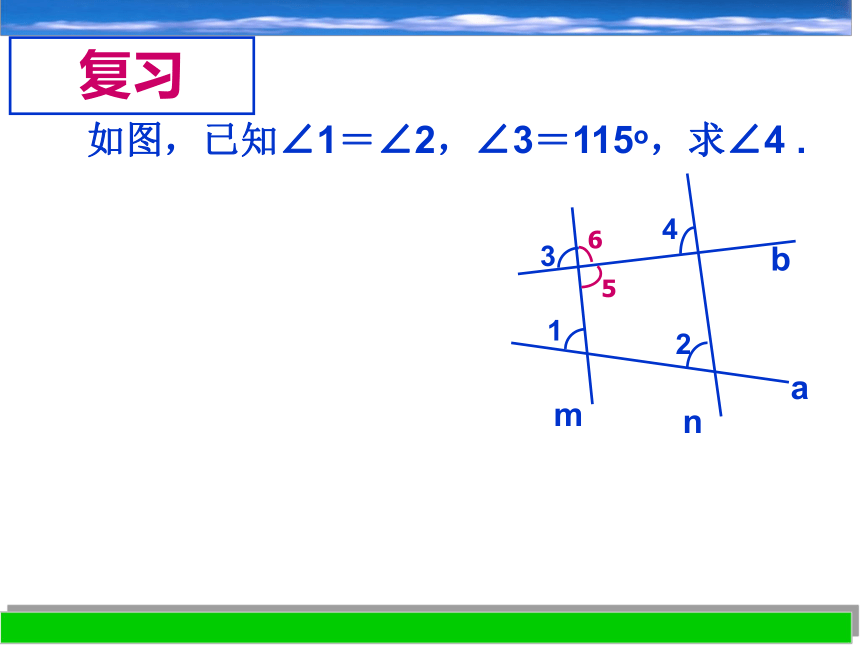
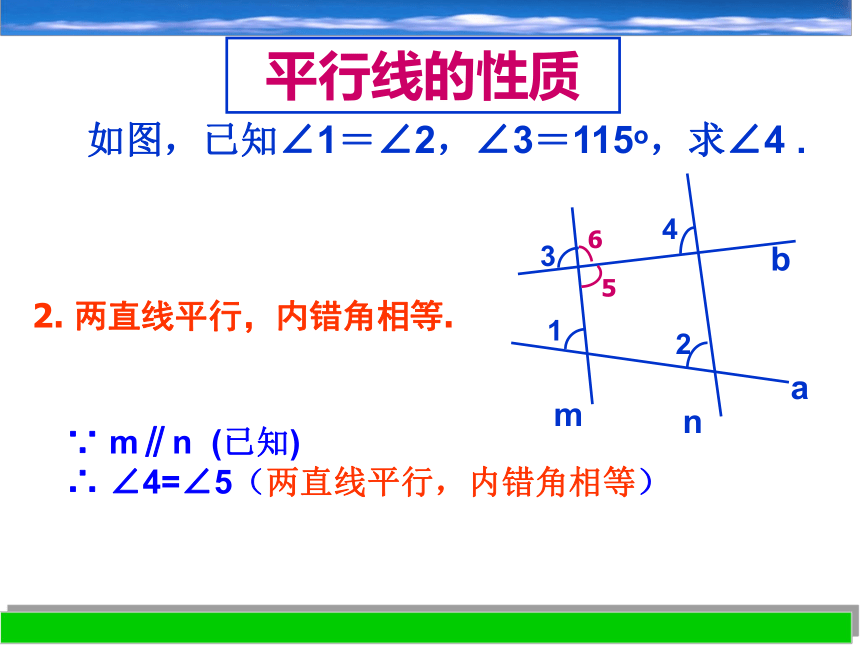
你发现平行线还有哪些性质?∠2=∠3,∠3+∠4=180°.⑴∠1=∠2.⑵∠3=∠1，∠4=∠2互补.平行线的性质还有“两直线平行，内错角相等”“两直线平行，同旁内角互补”.如图，已知∠1＝∠2，∠3＝115o，求∠4 .复习平行线的性质如图，已知∠1＝∠2，∠3＝115o，求∠4 .1. 两直线平行，同位角相等．3. 两直线平行，同旁内角互补．2. 两直线平行，内错角相等.平行线的性质如图，已知∠1＝∠2，∠3＝115o，求∠4 .2. 两直线平行，内错角相等.∵ m∥n (已知)
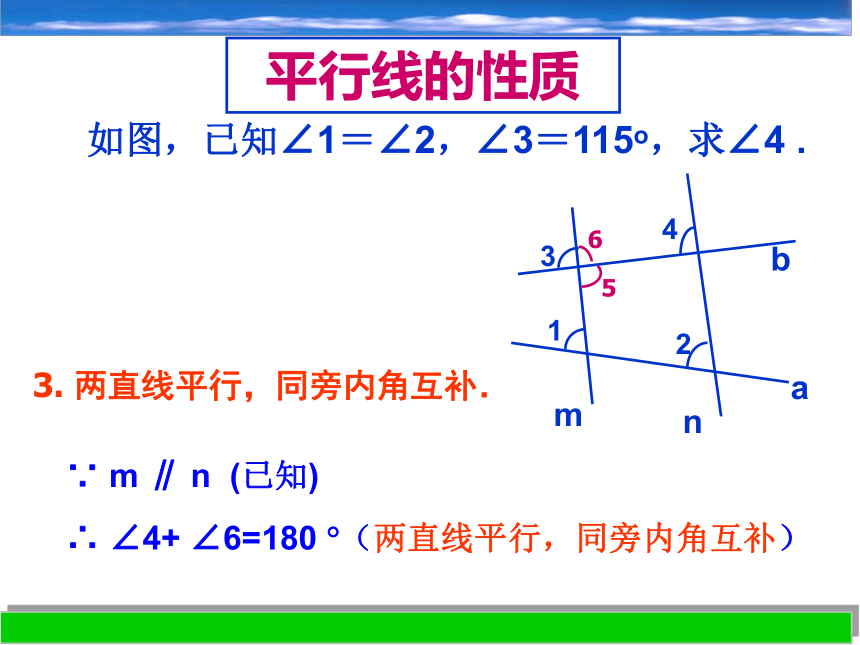
∴ ∠4=∠5（两直线平行，内错角相等）平行线的性质如图，已知∠1＝∠2，∠3＝115o，求∠4 .3. 两直线平行，同旁内角互补．∵ m ∥ n (已知)∴ ∠4+ ∠6=180 ?（两直线平行，同旁内角互补）平行线的性质如图，已知∠1＝∠2，∠3＝115o，求∠4 .你能用几何语言写出上题的解题过程吗？ 如图，已知∠1＝∠2，∠3＝65o ，
求∠4的度数?试一试例3 如图，已知AB∥CD，AD∥BC.
猜想∠1与∠2的关系，并说明理由.34解 ∠1=∠2.理由如下:
已知AB//CD,根据“两直线平行,同旁内角互补”,
得∠1+∠BAD=180°.
同理,由AD//BC,得∠2+∠BAD=180°.
根据“同角的补角相等”,得∠1=∠2.例4 如图，已知∠ABC＋∠C＝180°，BD平分∠ABC.
∠CBD与∠D相等吗？请说明理由.变式：已知∠ABC+∠C=180°，∠CBD=∠D，请说明BD为∠ABC的平分线.解 ∠CBD=∠D.理由如下:
∵ ∠ABC+∠C=180°,
根据“同旁内角互补,两直线平行”,
得AB//CD．
再根据“两直线平行,内错角相等”,
得∠D=∠ABD．
∵BD平分∠ABC,
∴∠CBD=∠ABD．
∴∠CBD=∠D.1.如图,在墙面上安装某一管道需经两次拐弯,拐弯后的管道与拐弯前的管道平行.若第一个弯道处∠B=142°,那么第二个弯道处∠C为多少度?为什么?
答案：∠C=∠B=142°
(两直线平行,内错角相等).2.如图,已知AB//CD,AD//BC.填空:
(1)∵AB//CD,根据“两直线平行,内错角相等”,
可得∠1=_____________．
(2)∵AD//BC,根据(_______________________),
可得∠2=_____________．∠D．两直线平行,内错角相等∠ACB.3.如图,已知∠1=∠2,∠3=65°. 求∠4的度数．解：
∵∠1=∠2(已知),∴ a//b(内错角相等,两直线平行),
∴ ∠3+∠4=180°(两直线平行,同旁内角互补),
∴ ∠4=180°-∠3=180°-65°=115°.4.如图,D是 BC 上的一点,DE//AB,交AC于点E,DF//AC,交AB于点F.若∠B+∠C=120°,求∠FDE的度数.∵ DF//AC(已知),∴ ∠EDC=∠B(两直线平行,同位角相等). 同理,由DF//AC,得∠FDB=∠C. ∵ ∠FDE+∠FDB+∠EDC=180°,∴ ∠FDE＝180°- (∠FDB+∠EDC)
＝18°-(∠C+∠B)=180°-120°＝60°.5.一艘船从O处出发,沿北偏东60°方向行驶至A,然后向正东方向行驶至 C 后又改变航向,朝与出发时相反的方向行驶至B.请画出该船的航线示意图,并求∠ACB的度数.航线示意图如图.∠ACB=30°. 已知:∠1＝∠2，∠C＝∠D，猜想DF与AC的位置关系，并说明理由.补充：∵ ∠1＝∠2，(已知),∴DB//EC(同位角相等，两直线平行),∴DF//AC∴∠C=∠DBA=∠D,
内错角相等，两直线平行 如图，已知AB//CD，∠B＝40°,∠D＝15°，则∠BED ＝ _______55° 辨一辨休息一会！请在此输入您的副标题