浙教版七年级下册因式分解复习

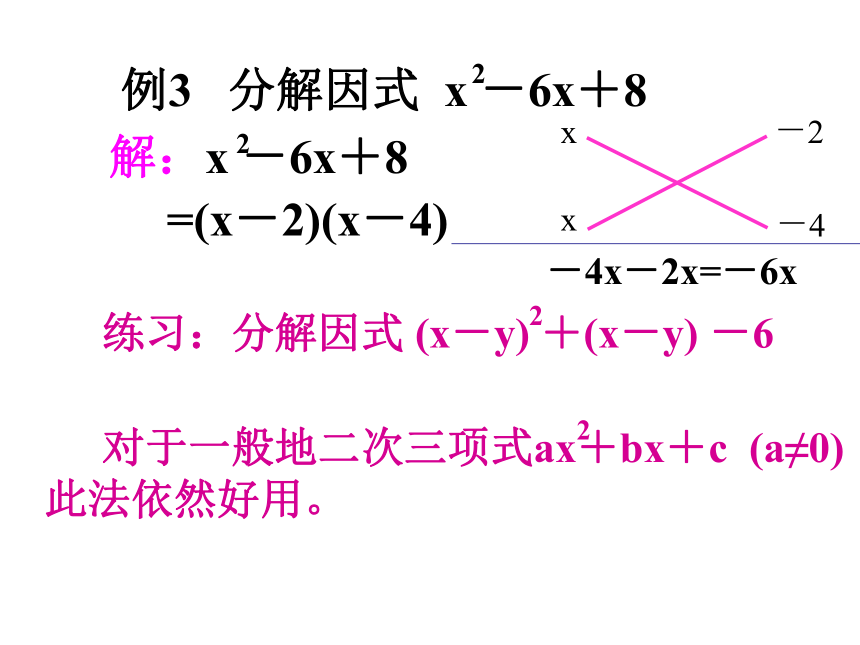
课件17张PPT。义务教育课程标准实验教科书浙教版数学因式分解（常用方法）巩固与拓展一、课本中出现的知识例1.
6(m+n) -2(m+n)
Xy(x+y)(x-y)-x(x-y)
A(a-b)-b(b-a)1.提取公因式22查一查 我学会了吗2.乘法公式例2.
4a +4ab
5a (20-5)222查一查 我学会了吗二、拓展与延伸合作交流 探索新知二、拓展与延伸3.十字相乘法x ＋(p＋q)x＋pq=(x＋p)(x＋q) 实际在使用此公式时，需要把一次项系数和常数项进行分拆，在试算时，会带来一些困难。
下面介绍的方法，正好解决了这个困难。=(x－2)(x－4)=(x－3)(3x－1)=(5x＋3)(x－4)练习：将下列各式分解因式答案(7x＋6)(x＋1)答案－ (y＋6)(y－2)答案 (3x－y)(5x＋4y)答案 (2x－1)(5x＋8)答案 (x－1)(x－a) =(2x ＋y)(x－2y)＋3x＋4y－2=(2x ＋y－1)(x－2y＋2)例8 把a2-ab+ac-bc分解因式分析：把这个多项式的四项按前两项与后两项分成两组，分别提出公因式a与c后，另一个因式正好都是a-b，这样就可以提出公因式a-b 。解：a2-ab+ac-bc=(a2-ab)+(ac-bc)=a(a-b)+c(a-b)=(a-b)(a+c)——分组——组内提公因式——提公因式4.分组分解法分析：把这个多项式的四项按前两项与后两项分成两组，并使两组的项都按x的降幂排列，然后从两组分别提出公因式2a与-b，这时，另一个因式正好都是x-5y，这样全式就可以提出公因式x-5y。解： 2ax-10ay+5by-bx=(2ax-10ay)+(5by-bx)=(2ax-10ay)+(-bx +5by）=2a(x-5y)-b(x- 5y)=(x-5y)(2a-b)例9 把2ax-10ay+5by-bx分解因式例8，例9种还有没有其他分组的方法；如果有，因式分解的结果是不是一样。例8解(2)：a2-ab+ac-bc=(a2+ac)-(ab+bc)=a(a+c)-b(a+c)= (a+c)(a-b)例9解(2)： 2ax-10ay+5by-bx=(2ax-bx)+(5by-10ay)=(2ax-bx)+(-10ay +5by）=x(2a-b)-5y(2a-b)= (2a-b)(x-5y)想一想 在有公因式的前提下，按对应项系数成比例分组，或按对应项的次数成比例分组。 (1)分组；(2)在各组内提公因式；(3)在各组之间进行因式分解(4)直至完全分解分组规律：分解步骤：把下列各式分解因式：(1)20(x+y)+x+y (2)p-q+k(p-q)(3)5m(a+b)-a-b (4)2m-2n-4x(m-n)解：原式 =20(x+y)+(x+y)
=21(x+y)解：原式=(p- q)+k(p-q)=(p-q)(1+k)解：原式=5m(a+b)-(a+b)=(a+b)(5m-1)解：原式=2(m-n)-4x(m-n)=(m-n)(2-4x)练习(5)ax+2by+cx-2ay-bx-2cy=(2by-2ay-2cy)+(ax+cx-bx)解：原式 解：原式=-2y(a-b+c)+x(a-b+c)=(a-b+c)(-2y+x)(6) x2-x2y+xy2-x+y-y2=(x2-y2)-(x2y-xy2)-(x-y)=(x-y)(x+y)-xy(x-y)-(x-y)=(x-y)(x+y-xy-1)=(x-y)[(x-xy)+(y-1)]=(x-y)[x(1-y)-(1-y)]=(x-y)(1-y)(x-1)