浙教版七年级数学下册课件:2.1二元一次方程(共23张PPT)
文档属性
| 名称 | 浙教版七年级数学下册课件:2.1二元一次方程(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-30 00:00:00 | ||
图片预览





文档简介
课件23张PPT。 “一切问题都可以转化为数学问题,一切数学问题都可以转化为代数问题,而一切代数问题又都可以转化为方程问题,因此,一旦解决了方程问题,一切问题将迎刃而解!”
------笛卡儿[Descartes, Rene du Perron, 1596-1650 ]想一想1、请用代数式表示:
x的3倍与y的4倍的和2、请用等式表示: x的3倍与y的4倍的和等于103x+4y3x+4y=10列出的上述等式是方程吗?问题1:这个问题中有几个未知量?问题2:能列一元一次方程求解吗? 问题3:如果设需要票额为6角的邮票x张,8角
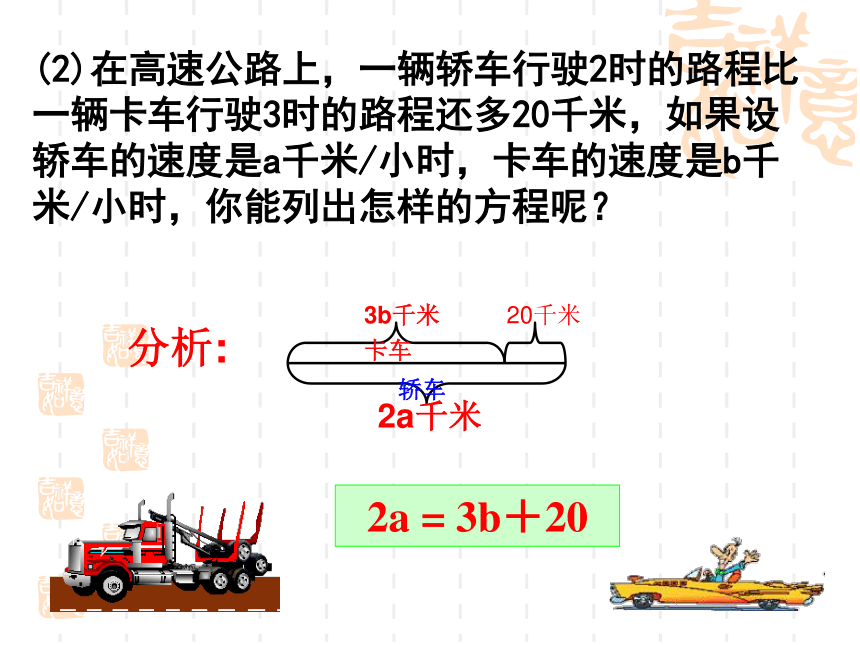
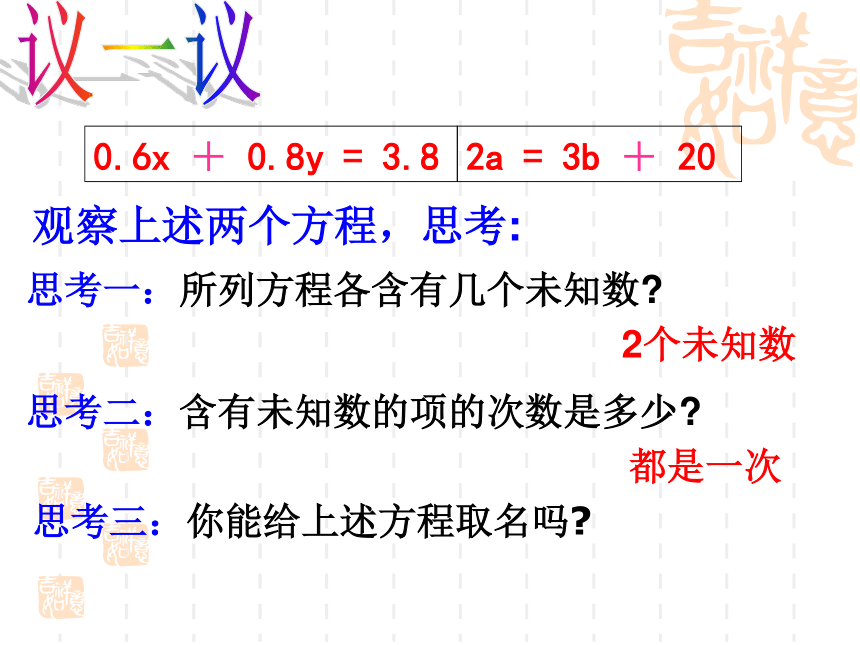
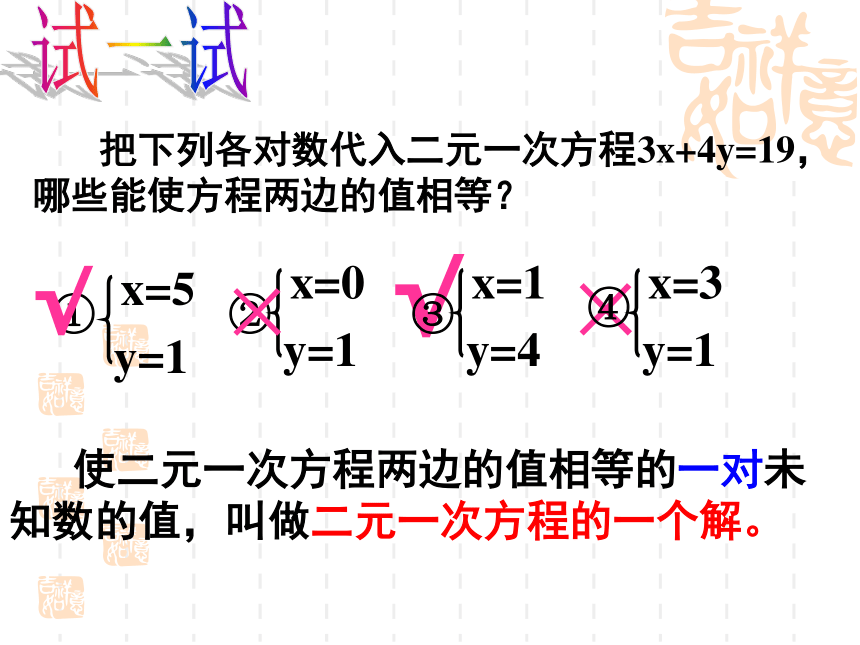
的邮票y张,你可以列出怎样的方程?0.6x+0.8y=3.8合作学习(2)在高速公路上,一辆轿车行驶2时的路程比一辆卡车行驶3时的路程还多20千米,如果设轿车的速度是a千米/小时,卡车的速度是b千米/小时,你能列出怎样的方程呢? 2a = 3b+20分析:0.6x + 0.8y = 3.82a = 3b + 20观察上述两个方程,思考: 思考一:所列方程各含有几个未知数?思考二:含有未知数的项的次数是多少?2个未知数都是一次议一议思考三:你能给上述方程取名吗?2.1 二元一次方程 含有两个未知数(二元),并且所含未知数的项的次数都是 1(一次) 的方程叫做二元一次方程.1、含未知数的项是一次单项式,是整式2、含有两个未知数(二元)3、含有未知数的项的次数都是1(一次)注:二元一次方程的概念马上练:课本P32判断下列各方程是不是二元一次方程?(2)3-2xy = 7(1)3-2x = 7(3)3e-2f = 7(4)3a-2b = 7b(5)3x2-2y = 7(6) ××××√√11反馈练习1 使二元一次方程两边的值相等的一对未知数的值,叫做二元一次方程的一个解。 把下列各对数代入二元一次方程3x+4y=19,哪些能使方程两边的值相等?试一试√×√×练一练1、下列各组数中是方程4x+y=10的解有A、4个;B、3个;C、2个;D、1个7√例已知方程 3x+2y=10 (1)用关于x的代数式表示y;(2)求当x=-2,0,3时,对应的y的值-3x3x+2y=10(1)解:移项,得 2y=10-3x (3)写出方程3x+2y=10的三个解。(2)解:y = 5 ×(-2) = 8 y = 5 ×0 = 5y = 5 ×3 =当x =-2时,当x = 0时,当x = 3时,学习交流 已知方程 2x+3y=10
(1)填写下表:642112(2)根据表格,写出方程的一个解。结论:二元一次方程有无数个解.说一说一元一次方程和二元一次方程的区别与联系: 一元一次方程 二元一次方程1、只含一个未知数2、通常只有一个解1、含有两个未知数2、通常有无数解1、都是整式方程2、含有未知数项,都是一次练一练2、已知二元一次方程2x+3y=2
(1)用含y的代数式表示x;解:(1)移项,得 2x=2-3y1-2402、已知二元一次方程2x+3y=2
(1)用含y的代数式表示x:
(2)根据给出的y值,求出相应的x的值,填入图内:对于二元一次方程2x+y=8,若x=2时y= ———,4注意:一般地,二元一次方程有无数个解。但在实际问题中经常会遇到求方程的正整数解。请你写出二元一次方程2x+y=8的其它正整数解——————— 。知识拓展1、假设有一根11米长的绳子,要把它剪成两段,问每一段要多少米?解:设两段绳子的长 度分别为x米,y米,
得这个二元一次方程有无数多个解。x+y=112、如果剪成的两段长度都是正整数米,怎样剪?1, 10 ; 2 , 9 ; 3, 8; 4, 7; 5; 6 .3、如果要剪成的两段,长的一段比短的一段长3米,怎样剪?4,74、如果剪成的三段长度都是正整数米,且这三段首尾顺次相接组成一个三角形,怎样剪?192837465522723624533534411111知识梳理本节课你学到了什么知识? 含有两个未知数,且含未知数的项的次数都是 一次的方程叫做二元一次方程.二元一次方程有无数个解. 使二元一次方程两边的值相等的一对未
知数的值,叫做二元一次方程的一个解.作业:见作业本(1)
------笛卡儿[Descartes, Rene du Perron, 1596-1650 ]想一想1、请用代数式表示:
x的3倍与y的4倍的和2、请用等式表示: x的3倍与y的4倍的和等于103x+4y3x+4y=10列出的上述等式是方程吗?问题1:这个问题中有几个未知量?问题2:能列一元一次方程求解吗? 问题3:如果设需要票额为6角的邮票x张,8角
的邮票y张,你可以列出怎样的方程?0.6x+0.8y=3.8合作学习(2)在高速公路上,一辆轿车行驶2时的路程比一辆卡车行驶3时的路程还多20千米,如果设轿车的速度是a千米/小时,卡车的速度是b千米/小时,你能列出怎样的方程呢? 2a = 3b+20分析:0.6x + 0.8y = 3.82a = 3b + 20观察上述两个方程,思考: 思考一:所列方程各含有几个未知数?思考二:含有未知数的项的次数是多少?2个未知数都是一次议一议思考三:你能给上述方程取名吗?2.1 二元一次方程 含有两个未知数(二元),并且所含未知数的项的次数都是 1(一次) 的方程叫做二元一次方程.1、含未知数的项是一次单项式,是整式2、含有两个未知数(二元)3、含有未知数的项的次数都是1(一次)注:二元一次方程的概念马上练:课本P32判断下列各方程是不是二元一次方程?(2)3-2xy = 7(1)3-2x = 7(3)3e-2f = 7(4)3a-2b = 7b(5)3x2-2y = 7(6) ××××√√11反馈练习1 使二元一次方程两边的值相等的一对未知数的值,叫做二元一次方程的一个解。 把下列各对数代入二元一次方程3x+4y=19,哪些能使方程两边的值相等?试一试√×√×练一练1、下列各组数中是方程4x+y=10的解有A、4个;B、3个;C、2个;D、1个7√例已知方程 3x+2y=10 (1)用关于x的代数式表示y;(2)求当x=-2,0,3时,对应的y的值-3x3x+2y=10(1)解:移项,得 2y=10-3x (3)写出方程3x+2y=10的三个解。(2)解:y = 5 ×(-2) = 8 y = 5 ×0 = 5y = 5 ×3 =当x =-2时,当x = 0时,当x = 3时,学习交流 已知方程 2x+3y=10
(1)填写下表:642112(2)根据表格,写出方程的一个解。结论:二元一次方程有无数个解.说一说一元一次方程和二元一次方程的区别与联系: 一元一次方程 二元一次方程1、只含一个未知数2、通常只有一个解1、含有两个未知数2、通常有无数解1、都是整式方程2、含有未知数项,都是一次练一练2、已知二元一次方程2x+3y=2
(1)用含y的代数式表示x;解:(1)移项,得 2x=2-3y1-2402、已知二元一次方程2x+3y=2
(1)用含y的代数式表示x:
(2)根据给出的y值,求出相应的x的值,填入图内:对于二元一次方程2x+y=8,若x=2时y= ———,4注意:一般地,二元一次方程有无数个解。但在实际问题中经常会遇到求方程的正整数解。请你写出二元一次方程2x+y=8的其它正整数解——————— 。知识拓展1、假设有一根11米长的绳子,要把它剪成两段,问每一段要多少米?解:设两段绳子的长 度分别为x米,y米,
得这个二元一次方程有无数多个解。x+y=112、如果剪成的两段长度都是正整数米,怎样剪?1, 10 ; 2 , 9 ; 3, 8; 4, 7; 5; 6 .3、如果要剪成的两段,长的一段比短的一段长3米,怎样剪?4,74、如果剪成的三段长度都是正整数米,且这三段首尾顺次相接组成一个三角形,怎样剪?192837465522723624533534411111知识梳理本节课你学到了什么知识? 含有两个未知数,且含未知数的项的次数都是 一次的方程叫做二元一次方程.二元一次方程有无数个解. 使二元一次方程两边的值相等的一对未
知数的值,叫做二元一次方程的一个解.作业:见作业本(1)
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
