第四章 因式分解综合题(基础)(含答案)
文档属性
| 名称 | 第四章 因式分解综合题(基础)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 70.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-08 17:29:59 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第四章 因式分解综合题(基础)
一、单选题
1.下列多项式能用平方差公式分解因式的是( )
A. B. C. D.
2.下列因式分解正确的是( )
A. B.
C. D.
3.下列由左边到右边的变形,是因式分解的是( )
A. B.
C. D.
4.如果代数式是完全平方式,则的值为( )
A.6 B. C.6或 D.6或2
5.对于①,②,从左到右的变形,表述正确的是( )
A.都是因式分解 B.都是乘法运算
C.①是因式分解,②是乘法运算 D.①是乘法运算,②是因式分解
6.如果是的一个因式,则m的值是( )
A. B.6 C. D.8
7.下列各式中从左到右的变形,是因式分解的是 ( )
A.(a+3)(a-3)=a2-9 B.x2+x-5=x(x+1)-5
C.x2+1=(x+1)(x-1) D.a2b+ab2=ab(a+b)
8.下列因式分解正确的是( )
A. B.
C. D.
9.在多项式中,先任意添加一个括号,再交换括号内首项和末项的符号,最后将所得式子化简,称之为“加换操作”.例如:,,…给出下列说法:
①存在某种“加换操作”,使其结果为;
②不存在某种“加换操作”,使其结果与原多项式的和为0;
③所有的“加换操作”共有8种不同的结果.
以上说法中正确的个数为( )
A.0 B.1 C.2 D.3
10.设 n是任意正整数,代入式子 n3-n中计算时,四名同学算出以下四个结果,其中正确的结果可能是 ( )
A.388 947 B.388 944 C.388 953 D.388 949
二、填空题
11.分解因式: .
12.多项式的公因式是 .
13.因式分解:3a2﹣27= .
14.分解因式:3x2﹣6x+3= .
15.定义:若数p可以表示成(x,y均为正整数)的形式,则称p为“希尔伯特”数.
例如:,,…所以39,147是“希尔伯特”数.
(1)有理数1 “希尔伯特”数(填“是”或“不是”);
(2)像39,147这样的“希尔伯特”数都可以用连续两个奇数按定义给出的运算表达出来,又称它们为“H希尔伯特”数.
①设连续两个奇数中较小的数是(n为正整数),用含n的代数式表示“H希尔伯特”数为 ;
②已知两个“H希尔伯特”数的差是48,则这两个“H希尔伯特”数中较大的是 .
16.已知关于x,y的二元一次方程组 (a,b为实数)。
(1)若x=2a-1,则a的值是 ;
(2)若x,y同时满足ax+by+4=0,2x+5y-ay=0,则a+b的值是 。
三、计算题
17.22×3.14+61×3.14+17×3.14.
18.分解因式:
(1)
(2)
19.利用因式分解进行计算
(1)
(2)
四、解答题
因式分解
20.;
21.
22.因式分解:
23.分解因式(在实数范围内): .
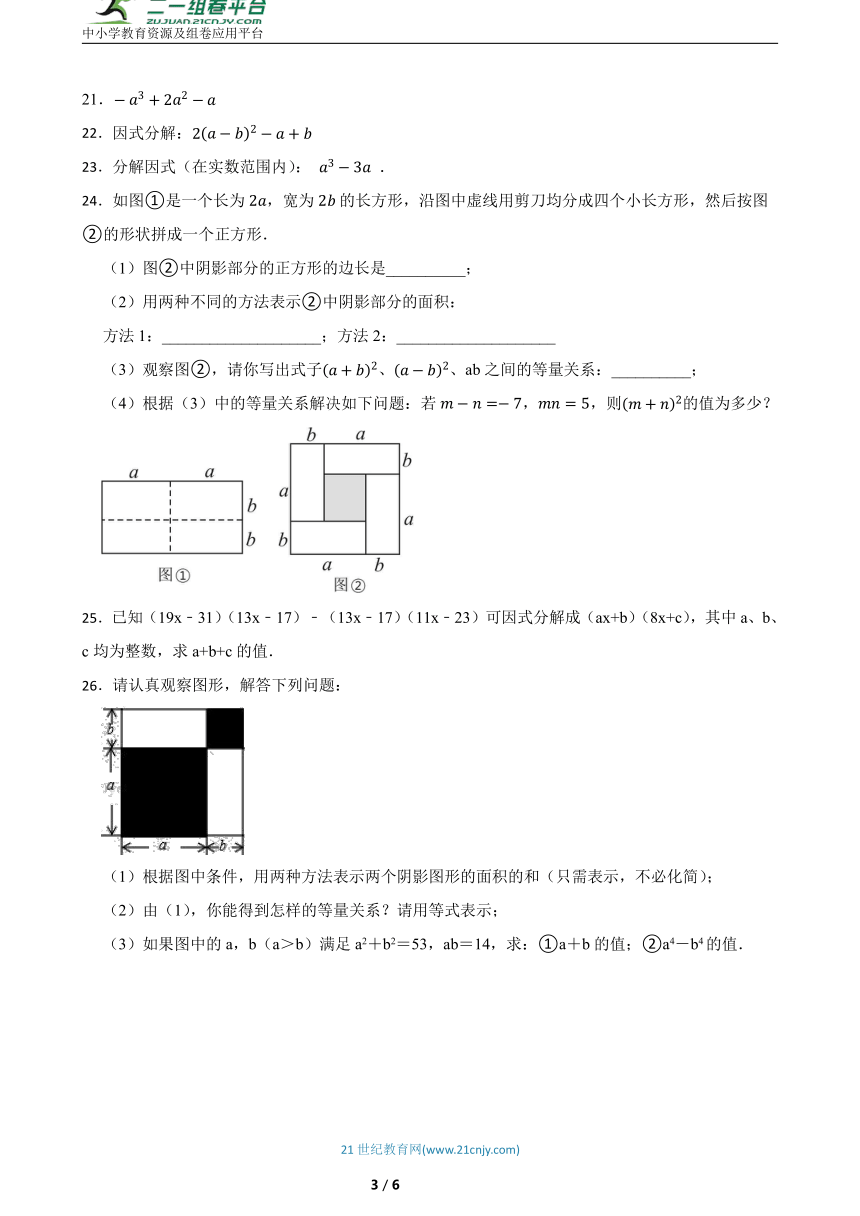
24.如图①是一个长为,宽为的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的形状拼成一个正方形.
(1)图②中阴影部分的正方形的边长是__________;
(2)用两种不同的方法表示②中阴影部分的面积:
方法1:____________________;方法2:____________________
(3)观察图②,请你写出式子、、ab之间的等量关系:__________;
(4)根据(3)中的等量关系解决如下问题:若,,则的值为多少?
25.已知(19x﹣31)(13x﹣17)﹣(13x﹣17)(11x﹣23)可因式分解成(ax+b)(8x+c),其中a、b、c均为整数,求a+b+c的值.
26.请认真观察图形,解答下列问题:
(1)根据图中条件,用两种方法表示两个阴影图形的面积的和(只需表示,不必化简);
(2)由(1),你能得到怎样的等量关系?请用等式表示;
(3)如果图中的a,b(a>b)满足a2+b2=53,ab=14,求:①a+b的值;②a4-b4的值.
答案解析部分
1.【答案】D
【知识点】因式分解﹣公式法
2.【答案】A
【知识点】因式分解﹣公式法;因式分解﹣综合运用提公因式与公式法
3.【答案】A
【知识点】因式分解的概念
4.【答案】C
【知识点】完全平方式
5.【答案】C
【知识点】完全平方公式及运用;因式分解的概念
6.【答案】A
【知识点】因式分解的概念
7.【答案】D
【知识点】因式分解的概念
8.【答案】D
【知识点】因式分解﹣公式法
9.【答案】D
【知识点】去括号法则及应用;添括号法则及应用
10.【答案】B
【知识点】因式分解的应用
11.【答案】
【知识点】因式分解﹣综合运用提公因式与公式法
12.【答案】
【知识点】公因式的概念
13.【答案】3(a+3)(a﹣3)
【知识点】平方差公式及应用;因式分解﹣提公因式法
14.【答案】3(x﹣1)2
【知识点】因式分解﹣综合运用提公因式与公式法
15.【答案】是;;67
【知识点】因式分解的应用;解二元一次方程组
16.【答案】(1)1
(2)8
【知识点】完全平方公式及运用;完全平方式;加减消元法解二元一次方程组
17.【答案】解:22×3.14+61×3.14+17×3.14
=3.14(22+61+17)
=3.14×100
=314.
【知识点】因式分解的应用
18.【答案】(1)解:
(2)解:
【知识点】因式分解﹣公式法;因式分解﹣综合运用提公因式与公式法
19.【答案】(1)解:原式
(2)解:原式
=3+7+11+15+19
=55
【知识点】因式分解的应用
【答案】20.
21.
【知识点】因式分解﹣综合运用提公因式与公式法
22.【答案】
【知识点】公因式的概念
23.【答案】解:a3 3a =a(a2-3)
= .
【知识点】实数范围内分解因式
24.【答案】(1);(2);;(3);(4)69
【知识点】多项式乘多项式;完全平方式
25.【答案】解:(19x﹣31)(13x﹣17)﹣(13x﹣17)(11x﹣23)
=(13x﹣17)[(19x﹣31)﹣(11x﹣23)]
=(13x﹣17)(8x﹣8)
∵(19x﹣31)(13x﹣17)﹣(13x﹣17)(11x﹣23)可因式分解成(ax+b)(8x+c),
∴a=13,b=﹣17,c=﹣8,
∴a+b+c=13﹣17﹣8=﹣12.
【知识点】代数式求值;公因式的概念;因式分解﹣提公因式法
26.【答案】(1)解:两个阴影图形的面积和可表示为:
a2+b2或 (a+b)2-2ab
(2)解:a2+b2=(a+b)2-2ab
(3)解:∵a,b(a>b)满足a2+b2=53,ab=14,
∴①(a+b)2=a2+b2+2ab
=53+2×14=81
∴a+b=±9,
又∵a>0,b>0,∴a+b=9.
②∵a4-b4=(a2+b2)(a+b)(a-b),
且∴a-b=±5
又∵a>b>0,
∴a-b=5,
∴a4﹣b4=(a2+b2)(a+b)(a-b)=53×9×5=2385.
【知识点】完全平方公式的几何背景;因式分解的应用
21世纪教育网(www.21cnjy.com)
2 / 6
第四章 因式分解综合题(基础)
一、单选题
1.下列多项式能用平方差公式分解因式的是( )
A. B. C. D.
2.下列因式分解正确的是( )
A. B.
C. D.
3.下列由左边到右边的变形,是因式分解的是( )
A. B.
C. D.
4.如果代数式是完全平方式,则的值为( )
A.6 B. C.6或 D.6或2
5.对于①,②,从左到右的变形,表述正确的是( )
A.都是因式分解 B.都是乘法运算
C.①是因式分解,②是乘法运算 D.①是乘法运算,②是因式分解
6.如果是的一个因式,则m的值是( )
A. B.6 C. D.8
7.下列各式中从左到右的变形,是因式分解的是 ( )
A.(a+3)(a-3)=a2-9 B.x2+x-5=x(x+1)-5
C.x2+1=(x+1)(x-1) D.a2b+ab2=ab(a+b)
8.下列因式分解正确的是( )
A. B.
C. D.
9.在多项式中,先任意添加一个括号,再交换括号内首项和末项的符号,最后将所得式子化简,称之为“加换操作”.例如:,,…给出下列说法:
①存在某种“加换操作”,使其结果为;
②不存在某种“加换操作”,使其结果与原多项式的和为0;
③所有的“加换操作”共有8种不同的结果.
以上说法中正确的个数为( )
A.0 B.1 C.2 D.3
10.设 n是任意正整数,代入式子 n3-n中计算时,四名同学算出以下四个结果,其中正确的结果可能是 ( )
A.388 947 B.388 944 C.388 953 D.388 949
二、填空题
11.分解因式: .
12.多项式的公因式是 .
13.因式分解:3a2﹣27= .
14.分解因式:3x2﹣6x+3= .
15.定义:若数p可以表示成(x,y均为正整数)的形式,则称p为“希尔伯特”数.
例如:,,…所以39,147是“希尔伯特”数.
(1)有理数1 “希尔伯特”数(填“是”或“不是”);
(2)像39,147这样的“希尔伯特”数都可以用连续两个奇数按定义给出的运算表达出来,又称它们为“H希尔伯特”数.
①设连续两个奇数中较小的数是(n为正整数),用含n的代数式表示“H希尔伯特”数为 ;
②已知两个“H希尔伯特”数的差是48,则这两个“H希尔伯特”数中较大的是 .
16.已知关于x,y的二元一次方程组 (a,b为实数)。
(1)若x=2a-1,则a的值是 ;
(2)若x,y同时满足ax+by+4=0,2x+5y-ay=0,则a+b的值是 。
三、计算题
17.22×3.14+61×3.14+17×3.14.
18.分解因式:
(1)
(2)
19.利用因式分解进行计算
(1)
(2)
四、解答题
因式分解
20.;
21.
22.因式分解:
23.分解因式(在实数范围内): .
24.如图①是一个长为,宽为的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的形状拼成一个正方形.
(1)图②中阴影部分的正方形的边长是__________;
(2)用两种不同的方法表示②中阴影部分的面积:
方法1:____________________;方法2:____________________
(3)观察图②,请你写出式子、、ab之间的等量关系:__________;
(4)根据(3)中的等量关系解决如下问题:若,,则的值为多少?
25.已知(19x﹣31)(13x﹣17)﹣(13x﹣17)(11x﹣23)可因式分解成(ax+b)(8x+c),其中a、b、c均为整数,求a+b+c的值.
26.请认真观察图形,解答下列问题:
(1)根据图中条件,用两种方法表示两个阴影图形的面积的和(只需表示,不必化简);
(2)由(1),你能得到怎样的等量关系?请用等式表示;
(3)如果图中的a,b(a>b)满足a2+b2=53,ab=14,求:①a+b的值;②a4-b4的值.
答案解析部分
1.【答案】D
【知识点】因式分解﹣公式法
2.【答案】A
【知识点】因式分解﹣公式法;因式分解﹣综合运用提公因式与公式法
3.【答案】A
【知识点】因式分解的概念
4.【答案】C
【知识点】完全平方式
5.【答案】C
【知识点】完全平方公式及运用;因式分解的概念
6.【答案】A
【知识点】因式分解的概念
7.【答案】D
【知识点】因式分解的概念
8.【答案】D
【知识点】因式分解﹣公式法
9.【答案】D
【知识点】去括号法则及应用;添括号法则及应用
10.【答案】B
【知识点】因式分解的应用
11.【答案】
【知识点】因式分解﹣综合运用提公因式与公式法
12.【答案】
【知识点】公因式的概念
13.【答案】3(a+3)(a﹣3)
【知识点】平方差公式及应用;因式分解﹣提公因式法
14.【答案】3(x﹣1)2
【知识点】因式分解﹣综合运用提公因式与公式法
15.【答案】是;;67
【知识点】因式分解的应用;解二元一次方程组
16.【答案】(1)1
(2)8
【知识点】完全平方公式及运用;完全平方式;加减消元法解二元一次方程组
17.【答案】解:22×3.14+61×3.14+17×3.14
=3.14(22+61+17)
=3.14×100
=314.
【知识点】因式分解的应用
18.【答案】(1)解:
(2)解:
【知识点】因式分解﹣公式法;因式分解﹣综合运用提公因式与公式法
19.【答案】(1)解:原式
(2)解:原式
=3+7+11+15+19
=55
【知识点】因式分解的应用
【答案】20.
21.
【知识点】因式分解﹣综合运用提公因式与公式法
22.【答案】
【知识点】公因式的概念
23.【答案】解:a3 3a =a(a2-3)
= .
【知识点】实数范围内分解因式
24.【答案】(1);(2);;(3);(4)69
【知识点】多项式乘多项式;完全平方式
25.【答案】解:(19x﹣31)(13x﹣17)﹣(13x﹣17)(11x﹣23)
=(13x﹣17)[(19x﹣31)﹣(11x﹣23)]
=(13x﹣17)(8x﹣8)
∵(19x﹣31)(13x﹣17)﹣(13x﹣17)(11x﹣23)可因式分解成(ax+b)(8x+c),
∴a=13,b=﹣17,c=﹣8,
∴a+b+c=13﹣17﹣8=﹣12.
【知识点】代数式求值;公因式的概念;因式分解﹣提公因式法
26.【答案】(1)解:两个阴影图形的面积和可表示为:
a2+b2或 (a+b)2-2ab
(2)解:a2+b2=(a+b)2-2ab
(3)解:∵a,b(a>b)满足a2+b2=53,ab=14,
∴①(a+b)2=a2+b2+2ab
=53+2×14=81
∴a+b=±9,
又∵a>0,b>0,∴a+b=9.
②∵a4-b4=(a2+b2)(a+b)(a-b),
且∴a-b=±5
又∵a>b>0,
∴a-b=5,
∴a4﹣b4=(a2+b2)(a+b)(a-b)=53×9×5=2385.
【知识点】完全平方公式的几何背景;因式分解的应用
21世纪教育网(www.21cnjy.com)
2 / 6
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
