专题五 多元一次方程组2024-2025学年浙教版七年级数学下册(含答案)
文档属性
| 名称 | 专题五 多元一次方程组2024-2025学年浙教版七年级数学下册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 268.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-14 19:06:15 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
专题五 多元一次方程组
知识梳理
多元一次方程组的解法与二元一次方程的解法类同,主要是用代入或者加减消元法,并结合数学整体思想,最终将多元方程组转化成为一元一次方程,实现未知数的求解。
【例1】解方程组
【例2】设x+y+z+u=1,(2x+y):1=(2y+z):2=(2z+u):3=(2u+x):4,则7x+3y+3z+u= ( )。
A.3 B.2 C.1.5 D.1.2
【例3】解下列方程组:
(3)求方程组的正整数解。
【例4】方程组 的解是 ( )。
【例5】解方程组
【例6】有若干个整数,若每两个整数之和为 361、380、381、382、383、400、401、402、420、422,则这些整数分别是 。
【例7】购买五种商品 A 、A 、A 、A 、A 的件数与总钱数列成下表:
品 次 名 数 A A A A A 总钱数
第一次购件数 1 3 4 5 6 1992 元
第二次购件数 1 5 7 9 11 2984元
求:购买每种商品各一件共需多少元
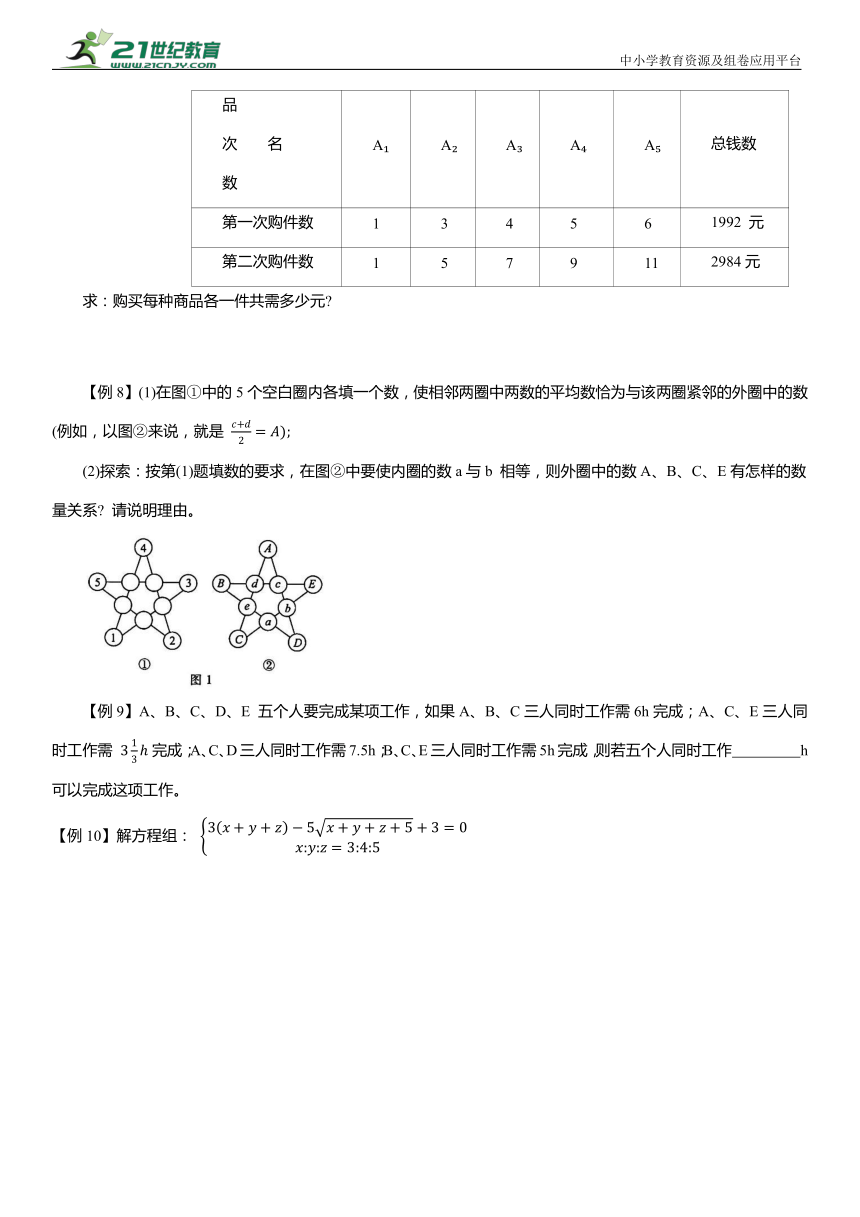
【例8】(1)在图①中的5个空白圈内各填一个数,使相邻两圈中两数的平均数恰为与该两圈紧邻的外圈中的数(例如,以图②来说,就是
(2)探索:按第(1)题填数的要求,在图②中要使内圈的数a与b 相等,则外圈中的数A、B、C、E有怎样的数量关系 请说明理由。
【例9】A、B、C、D、E 五个人要完成某项工作,如果A、B、C三人同时工作需6h完成;A、C、E三人同时工作需 完成;A、C、D三人同时工作需7.5h;B、C、E三人同时工作需5h完成,则若五个人同时工作 h可以完成这项工作。
【例10】解方程组:
答案
【例1】解:由原方程组得
∴x=5-2y=5-2(8-2z)=-11+4z=-11+4(11-2u)=33-8u=33-8(6-2x)=-15+16x
即x=-15+16x,解之得x=1,
将x=1代入⑧得u=4,
将u=4代入⑦得z=3,
将z=3代入⑥得 y=2。
【例2】解:设(2x+y):1=(2y+z):2=(2z+u):3=(2u+x):4=k,∴2x+y=k①;2y+z=2k②;2z+u=3k③;2u+x=4k④;①+②+③+④=3(x+y+z+u)=3=10k,
联立①②③④可得
∴可得:7x+3y+3z+u=2。
故选:B。
【例3】解:
①×②×③×④×⑤得
· ahede=+12.
(2)当xy≥0时,|x+y|=|x|+|y|,则原方程组可化为 此时无解;
当xy≤0时,|x+y|=|x|-|y|或|y|-|x|,
则原方程组可化为: 或
解得
①+②+③得, xy=45, xz=18, yz=10,
三式相乘得, xyz=9×2×5,
解得
【例4】解:由题意得:2(cx-by)=(bx+ cy),
将 A、B、C、D选项代入可得:A、B、D均不符合题意,
而当 代入满足2(cx-by)=(bx+ cy)。
故选:C。
【例5】解:令 原方程组化为:
由①+②得:2
把④代入②得:
把④,⑤代入②得
分别把④、⑤、⑥代入 可得
检验:把x、y、z的值代入原方程组的分母,不使分母为零,所以所得的值为原方程组的解。
原方程组的解为
【例6】解:根据每两个整数之和有10种可能可得共有5个整数,从而可设这五个整数为x、y、z、a、b(x∴可得
∵每两个整数之和为 361,380,381,382,383,400,401,402,420,422,
∴可得4(x+y+z+a+b)=361+380+381+382+383+400+401+402+420+422,
∴将x+y=361,a+b=422代入可得z=200,
代入可得:x=180,z=y=181,a=202,b=220。
故答案为:180,181,200,202,220。
【例7】解:设五种商品A 、A 、A 、A 、A 的价格依次为x、y、z、a、b,
则:
②-①得:2y+3z+4a+5b=992,③;
①-③得:x+y+z+a+b=1000。
答:购买每种商品各一件共需1000元。
【例8】解:(1)借图②的字母,有
各式相加,得:2(a+b+c+d+e)=30,
即a+b+c+e+d=15,
将①与②代入,得:a+6+10=15,
∴a=-1,b=5,c=1,d=7,e=3,
如图所示:
(2)设相邻两内圈中的数相等,设a=b,根据题意得:
b=2D-a,e=2C-a,c=2E-b=2E-2D+a,d=2B-e=2B-2C+a,
∴a=A+C+D-B-E,
同理可得:b=B+D+E-A-C,
∵a=b,
∴A+C=B+E。
【例9】解:设A的工作效率为x,B的工作效率为y,C的工作效率为z,D的工作效率为a,E的工作效率为b,
②-③得
①-③得
把③④代入④得2a+z=0,
∴a=0,z=0,
∴1÷(x+y+z+a+b)=3,
答:3h才能完成。
故答案为:3。
【例10】解:令
则
代入①得:
即
解得 (舍去),
∴x+y+z=9-5=4,
∵x: y:z=3:4:5,
∴方程组的解为
专题五 多元一次方程组
知识梳理
多元一次方程组的解法与二元一次方程的解法类同,主要是用代入或者加减消元法,并结合数学整体思想,最终将多元方程组转化成为一元一次方程,实现未知数的求解。
【例1】解方程组
【例2】设x+y+z+u=1,(2x+y):1=(2y+z):2=(2z+u):3=(2u+x):4,则7x+3y+3z+u= ( )。
A.3 B.2 C.1.5 D.1.2
【例3】解下列方程组:
(3)求方程组的正整数解。
【例4】方程组 的解是 ( )。
【例5】解方程组
【例6】有若干个整数,若每两个整数之和为 361、380、381、382、383、400、401、402、420、422,则这些整数分别是 。
【例7】购买五种商品 A 、A 、A 、A 、A 的件数与总钱数列成下表:
品 次 名 数 A A A A A 总钱数
第一次购件数 1 3 4 5 6 1992 元
第二次购件数 1 5 7 9 11 2984元
求:购买每种商品各一件共需多少元
【例8】(1)在图①中的5个空白圈内各填一个数,使相邻两圈中两数的平均数恰为与该两圈紧邻的外圈中的数(例如,以图②来说,就是
(2)探索:按第(1)题填数的要求,在图②中要使内圈的数a与b 相等,则外圈中的数A、B、C、E有怎样的数量关系 请说明理由。
【例9】A、B、C、D、E 五个人要完成某项工作,如果A、B、C三人同时工作需6h完成;A、C、E三人同时工作需 完成;A、C、D三人同时工作需7.5h;B、C、E三人同时工作需5h完成,则若五个人同时工作 h可以完成这项工作。
【例10】解方程组:
答案
【例1】解:由原方程组得
∴x=5-2y=5-2(8-2z)=-11+4z=-11+4(11-2u)=33-8u=33-8(6-2x)=-15+16x
即x=-15+16x,解之得x=1,
将x=1代入⑧得u=4,
将u=4代入⑦得z=3,
将z=3代入⑥得 y=2。
【例2】解:设(2x+y):1=(2y+z):2=(2z+u):3=(2u+x):4=k,∴2x+y=k①;2y+z=2k②;2z+u=3k③;2u+x=4k④;①+②+③+④=3(x+y+z+u)=3=10k,
联立①②③④可得
∴可得:7x+3y+3z+u=2。
故选:B。
【例3】解:
①×②×③×④×⑤得
· ahede=+12.
(2)当xy≥0时,|x+y|=|x|+|y|,则原方程组可化为 此时无解;
当xy≤0时,|x+y|=|x|-|y|或|y|-|x|,
则原方程组可化为: 或
解得
①+②+③得, xy=45, xz=18, yz=10,
三式相乘得, xyz=9×2×5,
解得
【例4】解:由题意得:2(cx-by)=(bx+ cy),
将 A、B、C、D选项代入可得:A、B、D均不符合题意,
而当 代入满足2(cx-by)=(bx+ cy)。
故选:C。
【例5】解:令 原方程组化为:
由①+②得:2
把④代入②得:
把④,⑤代入②得
分别把④、⑤、⑥代入 可得
检验:把x、y、z的值代入原方程组的分母,不使分母为零,所以所得的值为原方程组的解。
原方程组的解为
【例6】解:根据每两个整数之和有10种可能可得共有5个整数,从而可设这五个整数为x、y、z、a、b(x
∵每两个整数之和为 361,380,381,382,383,400,401,402,420,422,
∴可得4(x+y+z+a+b)=361+380+381+382+383+400+401+402+420+422,
∴将x+y=361,a+b=422代入可得z=200,
代入可得:x=180,z=y=181,a=202,b=220。
故答案为:180,181,200,202,220。
【例7】解:设五种商品A 、A 、A 、A 、A 的价格依次为x、y、z、a、b,
则:
②-①得:2y+3z+4a+5b=992,③;
①-③得:x+y+z+a+b=1000。
答:购买每种商品各一件共需1000元。
【例8】解:(1)借图②的字母,有
各式相加,得:2(a+b+c+d+e)=30,
即a+b+c+e+d=15,
将①与②代入,得:a+6+10=15,
∴a=-1,b=5,c=1,d=7,e=3,
如图所示:
(2)设相邻两内圈中的数相等,设a=b,根据题意得:
b=2D-a,e=2C-a,c=2E-b=2E-2D+a,d=2B-e=2B-2C+a,
∴a=A+C+D-B-E,
同理可得:b=B+D+E-A-C,
∵a=b,
∴A+C=B+E。
【例9】解:设A的工作效率为x,B的工作效率为y,C的工作效率为z,D的工作效率为a,E的工作效率为b,
②-③得
①-③得
把③④代入④得2a+z=0,
∴a=0,z=0,
∴1÷(x+y+z+a+b)=3,
答:3h才能完成。
故答案为:3。
【例10】解:令
则
代入①得:
即
解得 (舍去),
∴x+y+z=9-5=4,
∵x: y:z=3:4:5,
∴方程组的解为
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
