平行线培优拓展2024-2025学年浙教版七年级数学下册(含答案)
文档属性
| 名称 | 平行线培优拓展2024-2025学年浙教版七年级数学下册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 345.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-14 19:15:33 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
平行线培优拓展
一、选择题
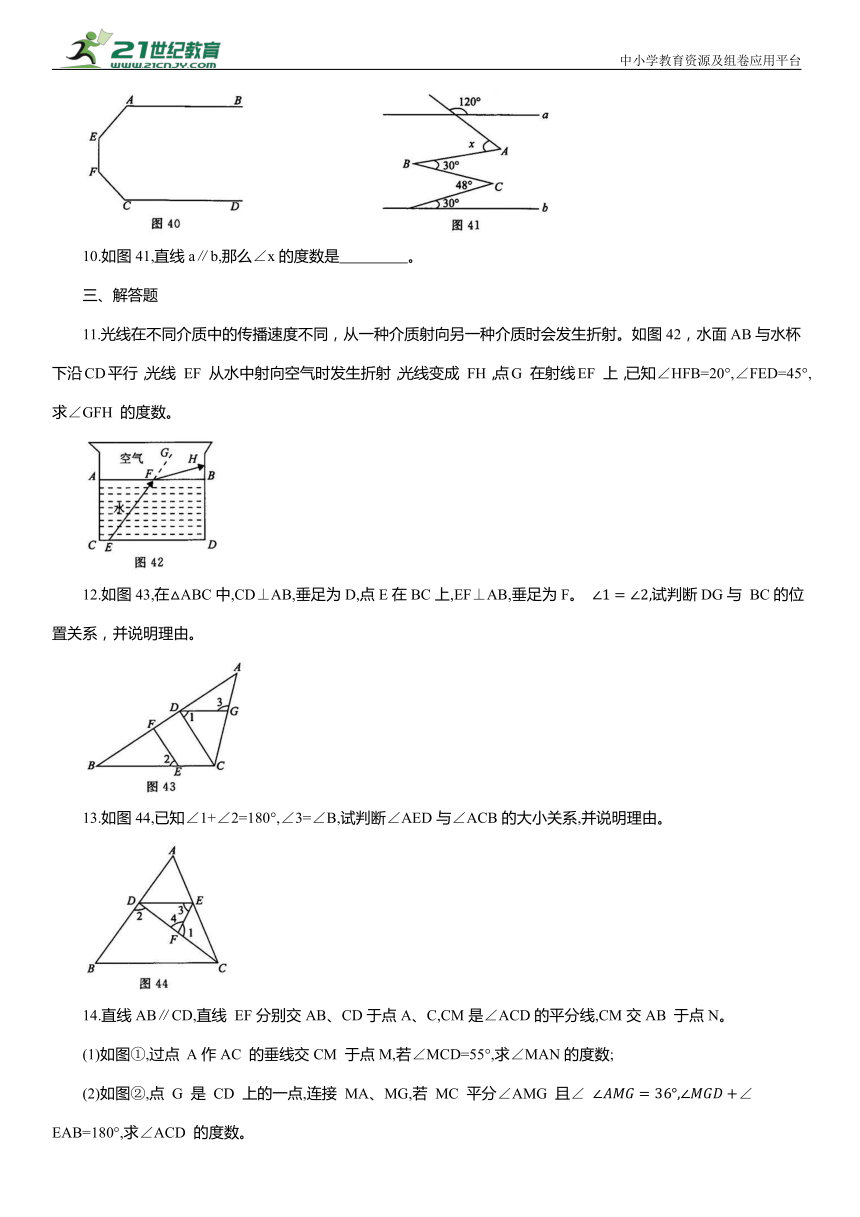
1.已知直线 l ∥l ,一块含30°角的直角三角板如图34所示放置,∠2=35°,则∠1等于 ( )。
A.25° B.35° C.40° D.45°
2.如图35,已知AB∥DE,∠ABC=75°,∠CDE=145°,则∠BCD的值为 ( )。
A.20° B.30° C.40° D.70°
3.如图36,CD∥AB,点O在AB 上,OE 平分∠BOD,OF⊥OE,∠D=110°,则∠AOF的度数是 ( )。
A.20° B.25° C.30° D.35°
4.如图37,直线l ∥l ,∠1=30°,则∠2+∠3= ( )。
A.150° B.180° C.210° D.240°
5.如图38,AB∥CD,BE平分∠ABC,CE⊥BE。若∠BCD=50°,则∠BCE的度数为 ( )。
A.55° B.65° C.70° D.75°
二、填空题
6.如图39所示,AD∥BC,BO、CO分别平分∠ABC、∠DCB,若∠A+∠D=225°,则∠BOC= 度。
7.已知两个角的两边互相平行,其中一个角的度数为40°,则另一个角的度数为 。
8.若平面上4条直线两两相交且无三线共点,则共有同旁内角 对。
9.如图40,AB∥CD,求∠BAE+∠AEF+∠EFC+∠FCD的度数是 。
10.如图41,直线a∥b,那么∠x的度数是 。
三、解答题
11.光线在不同介质中的传播速度不同,从一种介质射向另一种介质时会发生折射。如图42,水面AB与水杯下沿CD平行,光线 EF 从水中射向空气时发生折射,光线变成 FH,点G 在射线EF 上,已知∠HFB=20°,∠FED=45°,求∠GFH 的度数。
12.如图43,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F。 试判断DG与 BC的位置关系,并说明理由。
13.如图44,已知∠1+∠2=180°,∠3=∠B,试判断∠AED与∠ACB的大小关系,并说明理由。
14.直线AB∥CD,直线 EF分别交AB、CD于点A、C,CM是∠ACD的平分线,CM交AB 于点N。
(1)如图①,过点 A作AC 的垂线交CM 于点M,若∠MCD=55°,求∠MAN的度数;
(2)如图②,点 G 是 CD 上的一点,连接 MA、MG,若 MC 平分∠AMG 且∠ ∠EAB=180°,求∠ACD 的度数。
15.如图46,直线AC∥BD,连接AB,直线AC、BD 及线段AB 把平面分成①、②、③、④四个部分,规定:线上各点不属于任何部分。当动点 P 落在某个部分时,连接 PA、PB,构成 三个角。(提示:有公共端点的两条重合的射线所组成的角是0°角)
(1)当动点 P 落在第①部分时,求证:
(2)当动点 P 落在第②部分时, 是否成立 (直接回答成立或不成立)
(3)当动点 P 落在第③部分时,全面探究 之间的关系,并写出动点 P 的具体位置和相应的结论。选择其中一种结论加以证明。
答案
一、选择题
1.解:过C作CM∥直线l ,
∵直线l ∥l ,
∴CM∥直线l ∥直线l ,
∵∠ACB=60°,∠2=35°,
∴∠2=∠ACM=35°,
∴∠1=∠MCB=∠ACB-∠ACM=60°-35°=25°,故选:A。
2.解:延长ED交BC 于F,如图所示:
∵AB∥DE,∠ABC=75°,
∴∠MFC=∠B=75°,
∵∠CDE=145°,
∴∠FDC=180°-145°=35°,
∴∠C=∠MFC-∠MDC=75°-35°=40°,
故选:C。
3.解:∵CD∥AB,∴∠AOD+∠D=180°,
∴∠AOD=70°,
∴∠DOB=110°,
∵OE平分∠BOD,
∴∠DOE=55°,
∵OF⊥OE,
∴∠FOE=90°,
∴∠DOF=90°-55°=35°,
∴∠AOF=70°-35°=35°,
故选:D。
4.解:如图,过点 E作EF∥l ,
∵l ∥l ,EF∥l ,
∴EF∥l ∥l ,
∴∠1=∠AEF=30°,
∠FEC+∠3=180°,
∴∠2+∠3=∠AEF+∠FEC+∠3=30°+180°=210°,故选:C。
5.解:∵AB∥CD,∠BCD=50°,
∴∠ABC=50°,
∵BE平分∠ABC,
∴∠EBC=25°,
∵CE⊥BE,
∴∠BCE=90°-25°=65°,
故选:B。
二、填空题
6.解:∵AD∥BC,
∴∠A+∠ABC=180°,∠D+∠DCB=180°,
∵∠A+∠D=225°,
∴∠ABC+∠DCB=135°,
∵BO,CO分别平分∠ABC,∠DCB,
∴∠BOC=180°-(∠OBC+∠OCB)=112.5°,故答案为:112.5°。
7.解:∵两个角的两边互相平行,
∴这两个角互补或相等,
∵其中一个角为40°,
∴另一个角的度数为:40°或140°。
故答案为:40°或140°。
8.解:如图,
∵平面上4条直线两两相交且无三线共点,
∴共有3×4=12条线段。
又∵每条线段两侧各有一对同旁内角,∴共有同旁内角12×2=24对。
故答案为:24。
9.解:如图,过点 E作EM∥AB,过点 F作FN∥AB,
∵AB∥CD,
∴EM∥FN∥AB∥CD,
∴∠A+∠1=180°,.∠2+∠3=180°,∠4+∠C=180°,
∴∠BAE+∠AEF+∠EFC+∠FCD=∠A+∠1+∠2+∠3+∠4+∠C=540°。
故答案为:540°。
10.解:如图,过A作AE∥a,过B作BF∥a,过C作CR∥a,
∵直线a∥b,
∴直线a∥b∥ AE∥BF∥CR,
∴∠RCT=∠CTZ=30°,
∵∠BCT=48°,
∴∠BCR=48°-30°=18°,
∴∠RCB=∠CBF=18°,
∴∠ABF=30°-18°=12°=∠EAB,
∵∠QWY=120°,
∴∠YWA=180°-∠QWY=60°,
∴∠WAE=∠YWA=60°,
∴x=∠WAE+∠EAB=60°+12°=72°,故答案为:72°。
三、解答题
11.解:∵AB∥CD,
∴∠GFB=∠FED=45°。
∵∠HFB=20°,
∴∠GFH=∠GFB-∠HFB=45°-20°=25°。
12.解:DG∥BC,理由如下:
∵CD⊥AB,EF⊥AB,
∴CD∥EF,
∴∠2=∠DCE,
∵∠1=∠2,
∴∠1=∠DCE,
∴DG∥BC。
13.解:∠AED=∠ACB。
理由:∵∠1+∠4=180°(平角定义),∠1+∠2=180°(已知),
∴∠2=∠4,
∴EF∥AB(内错角相等,两直线平行),
∴∠3=∠ADE(两直线平行,内错角相等),
∵∠3=∠B(已知),
∴∠B=∠ADE(等量代换),
∴DE∥BC(同位角相等,两直线平行),
∴∠AED=∠ACB(两直线平行,同位角相等)。
14.解:(1)如图①
∵CM是∠ACD的平分线,∠MCD=55°,
∴∠ACD=2∠MCD=110°,
又∵AB∥CD,
又∵AM⊥EF,
(2)如图②
∵MC平分∠AMG 且∠AMG=36°,
∴∠CMG=18°,
∵MC平分∠ACG,
∵∠CAB+∠EAB=180°,∠MGD+∠EAB=180°,
∴∠BAC=∠MGD,
∵AB∥CD,
∴∠BAC+∠ACD=180°,
设∠ACD=α,
则
∵∠MGD 是△CMG的外角,
∴∠MGD=∠CMG+∠MCG,即 解得α=108°,
∴∠ACD=108°。
15.解:
(1)解法一:如图a,延长 BP 交直线AC于点E,
∵AC∥BD,
∴∠PEA=∠PBD,
∵∠APB=∠PAE+∠PEA,
∴∠APB=∠PAC+∠PBD;
解法二:如图b,过点 P作FP∥AC,
∴∠PAC=∠APF,
∵AC∥BD,
∴FP∥BD,
∴∠FPB=∠PBD,
∴∠APB=∠APF+∠FPB=∠PAC+∠PBD;
解法三:如图c,
∵AC∥BD,
∴∠CAB+∠ABD=180°,∠PAC+∠PAB+∠PBA+∠PBD=180°,又∵∠APB+∠PBA+∠PAB=180°,
∴∠APB=∠PAC+∠PBD。
(2)不成立。
(3)(a)当动点 P 在射线 BA 的右侧时,结论是:
∠PBD=∠PAC+∠APB。
(b)当动点 P 在射线BA 上,结论是:
∠PBD=∠PAC+∠APB 或∠PAC=∠PBD+∠APB 或∠APB=0°,∠PAC=∠PBD(任写一个即可)。
(c)当动点 P 在射线BA 的左侧时,
结论是∠PAC=∠APB+∠PBD。
选择(a)证明:
如图d,连接 PA,连接 PB交AC 于M,
∵AC∥BD,
∴∠PMC=∠PBD,
又∵∠PMC=∠PAM+∠APM(三角形的一个外角等于与它不相邻的两个内角的和),
∴∠PBD=∠PAC+∠APB;
选择(b)证明:如图e,
∵点 P 在射线BA 上,
∴∠APB=0度,
∵AC∥BD,
∴∠PBD=∠PAC,
∴∠PBD=∠PAC+∠APB或∠PAC=∠PBD+∠APB或∠APB=0°,∠PAC=∠PBD;
选择(c)证明:
如图 f,连接PA,连接PB交AC于F,
∵AC∥BD,
∴∠PFA=∠PBD,
∵∠PAC=∠APF+∠PFA,
∴∠PAC=∠APB+∠PBD。
平行线培优拓展
一、选择题
1.已知直线 l ∥l ,一块含30°角的直角三角板如图34所示放置,∠2=35°,则∠1等于 ( )。
A.25° B.35° C.40° D.45°
2.如图35,已知AB∥DE,∠ABC=75°,∠CDE=145°,则∠BCD的值为 ( )。
A.20° B.30° C.40° D.70°
3.如图36,CD∥AB,点O在AB 上,OE 平分∠BOD,OF⊥OE,∠D=110°,则∠AOF的度数是 ( )。
A.20° B.25° C.30° D.35°
4.如图37,直线l ∥l ,∠1=30°,则∠2+∠3= ( )。
A.150° B.180° C.210° D.240°
5.如图38,AB∥CD,BE平分∠ABC,CE⊥BE。若∠BCD=50°,则∠BCE的度数为 ( )。
A.55° B.65° C.70° D.75°
二、填空题
6.如图39所示,AD∥BC,BO、CO分别平分∠ABC、∠DCB,若∠A+∠D=225°,则∠BOC= 度。
7.已知两个角的两边互相平行,其中一个角的度数为40°,则另一个角的度数为 。
8.若平面上4条直线两两相交且无三线共点,则共有同旁内角 对。
9.如图40,AB∥CD,求∠BAE+∠AEF+∠EFC+∠FCD的度数是 。
10.如图41,直线a∥b,那么∠x的度数是 。
三、解答题
11.光线在不同介质中的传播速度不同,从一种介质射向另一种介质时会发生折射。如图42,水面AB与水杯下沿CD平行,光线 EF 从水中射向空气时发生折射,光线变成 FH,点G 在射线EF 上,已知∠HFB=20°,∠FED=45°,求∠GFH 的度数。
12.如图43,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F。 试判断DG与 BC的位置关系,并说明理由。
13.如图44,已知∠1+∠2=180°,∠3=∠B,试判断∠AED与∠ACB的大小关系,并说明理由。
14.直线AB∥CD,直线 EF分别交AB、CD于点A、C,CM是∠ACD的平分线,CM交AB 于点N。
(1)如图①,过点 A作AC 的垂线交CM 于点M,若∠MCD=55°,求∠MAN的度数;
(2)如图②,点 G 是 CD 上的一点,连接 MA、MG,若 MC 平分∠AMG 且∠ ∠EAB=180°,求∠ACD 的度数。
15.如图46,直线AC∥BD,连接AB,直线AC、BD 及线段AB 把平面分成①、②、③、④四个部分,规定:线上各点不属于任何部分。当动点 P 落在某个部分时,连接 PA、PB,构成 三个角。(提示:有公共端点的两条重合的射线所组成的角是0°角)
(1)当动点 P 落在第①部分时,求证:
(2)当动点 P 落在第②部分时, 是否成立 (直接回答成立或不成立)
(3)当动点 P 落在第③部分时,全面探究 之间的关系,并写出动点 P 的具体位置和相应的结论。选择其中一种结论加以证明。
答案
一、选择题
1.解:过C作CM∥直线l ,
∵直线l ∥l ,
∴CM∥直线l ∥直线l ,
∵∠ACB=60°,∠2=35°,
∴∠2=∠ACM=35°,
∴∠1=∠MCB=∠ACB-∠ACM=60°-35°=25°,故选:A。
2.解:延长ED交BC 于F,如图所示:
∵AB∥DE,∠ABC=75°,
∴∠MFC=∠B=75°,
∵∠CDE=145°,
∴∠FDC=180°-145°=35°,
∴∠C=∠MFC-∠MDC=75°-35°=40°,
故选:C。
3.解:∵CD∥AB,∴∠AOD+∠D=180°,
∴∠AOD=70°,
∴∠DOB=110°,
∵OE平分∠BOD,
∴∠DOE=55°,
∵OF⊥OE,
∴∠FOE=90°,
∴∠DOF=90°-55°=35°,
∴∠AOF=70°-35°=35°,
故选:D。
4.解:如图,过点 E作EF∥l ,
∵l ∥l ,EF∥l ,
∴EF∥l ∥l ,
∴∠1=∠AEF=30°,
∠FEC+∠3=180°,
∴∠2+∠3=∠AEF+∠FEC+∠3=30°+180°=210°,故选:C。
5.解:∵AB∥CD,∠BCD=50°,
∴∠ABC=50°,
∵BE平分∠ABC,
∴∠EBC=25°,
∵CE⊥BE,
∴∠BCE=90°-25°=65°,
故选:B。
二、填空题
6.解:∵AD∥BC,
∴∠A+∠ABC=180°,∠D+∠DCB=180°,
∵∠A+∠D=225°,
∴∠ABC+∠DCB=135°,
∵BO,CO分别平分∠ABC,∠DCB,
∴∠BOC=180°-(∠OBC+∠OCB)=112.5°,故答案为:112.5°。
7.解:∵两个角的两边互相平行,
∴这两个角互补或相等,
∵其中一个角为40°,
∴另一个角的度数为:40°或140°。
故答案为:40°或140°。
8.解:如图,
∵平面上4条直线两两相交且无三线共点,
∴共有3×4=12条线段。
又∵每条线段两侧各有一对同旁内角,∴共有同旁内角12×2=24对。
故答案为:24。
9.解:如图,过点 E作EM∥AB,过点 F作FN∥AB,
∵AB∥CD,
∴EM∥FN∥AB∥CD,
∴∠A+∠1=180°,.∠2+∠3=180°,∠4+∠C=180°,
∴∠BAE+∠AEF+∠EFC+∠FCD=∠A+∠1+∠2+∠3+∠4+∠C=540°。
故答案为:540°。
10.解:如图,过A作AE∥a,过B作BF∥a,过C作CR∥a,
∵直线a∥b,
∴直线a∥b∥ AE∥BF∥CR,
∴∠RCT=∠CTZ=30°,
∵∠BCT=48°,
∴∠BCR=48°-30°=18°,
∴∠RCB=∠CBF=18°,
∴∠ABF=30°-18°=12°=∠EAB,
∵∠QWY=120°,
∴∠YWA=180°-∠QWY=60°,
∴∠WAE=∠YWA=60°,
∴x=∠WAE+∠EAB=60°+12°=72°,故答案为:72°。
三、解答题
11.解:∵AB∥CD,
∴∠GFB=∠FED=45°。
∵∠HFB=20°,
∴∠GFH=∠GFB-∠HFB=45°-20°=25°。
12.解:DG∥BC,理由如下:
∵CD⊥AB,EF⊥AB,
∴CD∥EF,
∴∠2=∠DCE,
∵∠1=∠2,
∴∠1=∠DCE,
∴DG∥BC。
13.解:∠AED=∠ACB。
理由:∵∠1+∠4=180°(平角定义),∠1+∠2=180°(已知),
∴∠2=∠4,
∴EF∥AB(内错角相等,两直线平行),
∴∠3=∠ADE(两直线平行,内错角相等),
∵∠3=∠B(已知),
∴∠B=∠ADE(等量代换),
∴DE∥BC(同位角相等,两直线平行),
∴∠AED=∠ACB(两直线平行,同位角相等)。
14.解:(1)如图①
∵CM是∠ACD的平分线,∠MCD=55°,
∴∠ACD=2∠MCD=110°,
又∵AB∥CD,
又∵AM⊥EF,
(2)如图②
∵MC平分∠AMG 且∠AMG=36°,
∴∠CMG=18°,
∵MC平分∠ACG,
∵∠CAB+∠EAB=180°,∠MGD+∠EAB=180°,
∴∠BAC=∠MGD,
∵AB∥CD,
∴∠BAC+∠ACD=180°,
设∠ACD=α,
则
∵∠MGD 是△CMG的外角,
∴∠MGD=∠CMG+∠MCG,即 解得α=108°,
∴∠ACD=108°。
15.解:
(1)解法一:如图a,延长 BP 交直线AC于点E,
∵AC∥BD,
∴∠PEA=∠PBD,
∵∠APB=∠PAE+∠PEA,
∴∠APB=∠PAC+∠PBD;
解法二:如图b,过点 P作FP∥AC,
∴∠PAC=∠APF,
∵AC∥BD,
∴FP∥BD,
∴∠FPB=∠PBD,
∴∠APB=∠APF+∠FPB=∠PAC+∠PBD;
解法三:如图c,
∵AC∥BD,
∴∠CAB+∠ABD=180°,∠PAC+∠PAB+∠PBA+∠PBD=180°,又∵∠APB+∠PBA+∠PAB=180°,
∴∠APB=∠PAC+∠PBD。
(2)不成立。
(3)(a)当动点 P 在射线 BA 的右侧时,结论是:
∠PBD=∠PAC+∠APB。
(b)当动点 P 在射线BA 上,结论是:
∠PBD=∠PAC+∠APB 或∠PAC=∠PBD+∠APB 或∠APB=0°,∠PAC=∠PBD(任写一个即可)。
(c)当动点 P 在射线BA 的左侧时,
结论是∠PAC=∠APB+∠PBD。
选择(a)证明:
如图d,连接 PA,连接 PB交AC 于M,
∵AC∥BD,
∴∠PMC=∠PBD,
又∵∠PMC=∠PAM+∠APM(三角形的一个外角等于与它不相邻的两个内角的和),
∴∠PBD=∠PAC+∠APB;
选择(b)证明:如图e,
∵点 P 在射线BA 上,
∴∠APB=0度,
∵AC∥BD,
∴∠PBD=∠PAC,
∴∠PBD=∠PAC+∠APB或∠PAC=∠PBD+∠APB或∠APB=0°,∠PAC=∠PBD;
选择(c)证明:
如图 f,连接PA,连接PB交AC于F,
∵AC∥BD,
∴∠PFA=∠PBD,
∵∠PAC=∠APF+∠PFA,
∴∠PAC=∠APB+∠PBD。
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
