1.1 直线的相交(2) 课件(共26张PPT)
文档属性
| 名称 | 1.1 直线的相交(2) 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-14 12:42:12 | ||
图片预览




文档简介
(共26张PPT)
1.1 直线的相交(2)
浙教版七年级下册
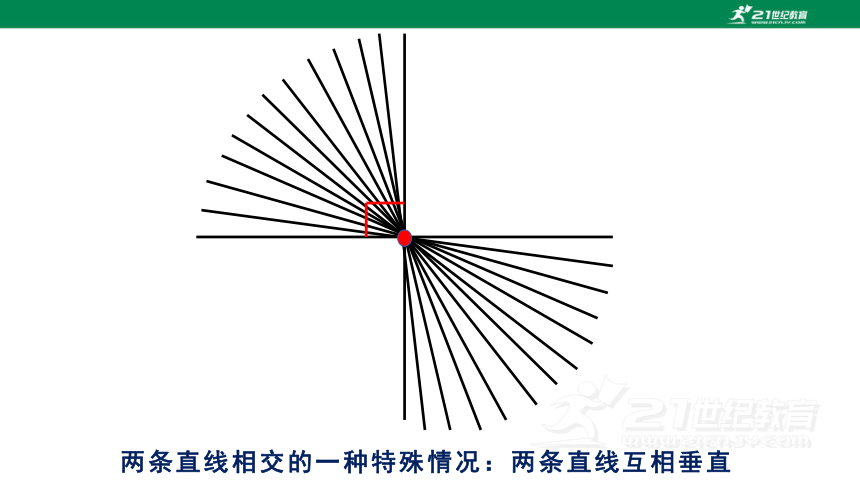
两条直线相交的一种特殊情况:两条直线互相垂直
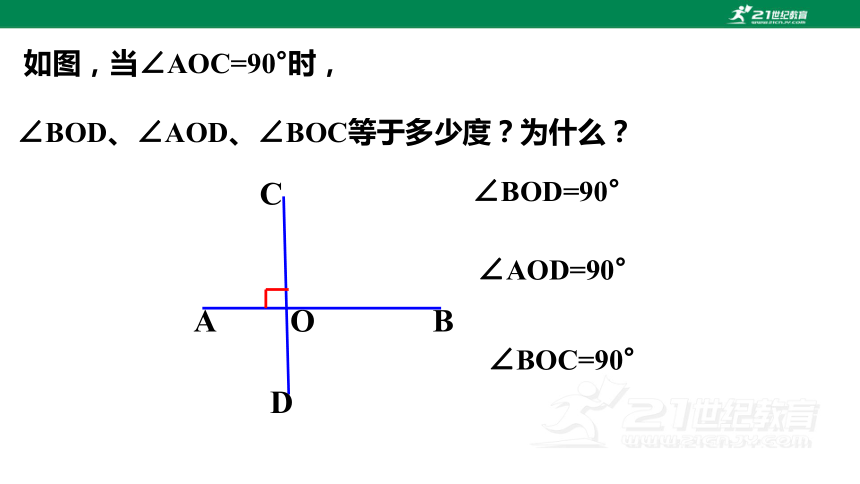
如图,当∠AOC=90°时,
∠BOD、∠AOD、∠BOC等于多少度?为什么?
A
B
C
D
O
∠BOD=90°
∠AOD=90°
∠BOC=90°
1.垂线的定义:当两条直线相交所成的四个角中,如果有一个角是 ,
其他三个角也都为 ,此时,这两条直线 .
其中一条直线叫做另一条直线的 .交点叫做 .
直角
互相垂直
垂线
垂足
直角
b
a
O
a、b互相垂直,O叫垂足.
a叫b的垂线,b也叫a的垂线.
垂足
b
a
O
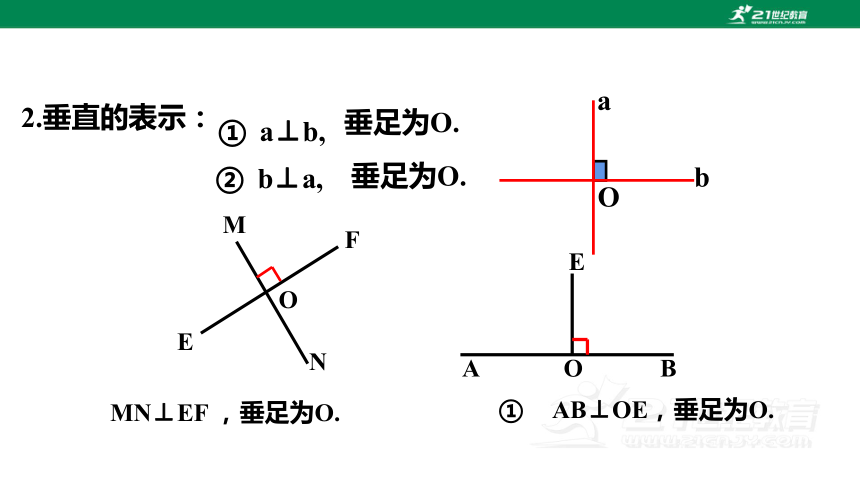
2.垂直的表示:
① a⊥b,
垂足为O.
② b⊥a,
垂足为O.
F
E
M
N
O
MN⊥EF ,垂足为O.
A
B
O
E
① AB⊥OE,垂足为O.
∵∠AOC=90°
如果直线AB、CD 相交于点O,∠AOC=90°,那么 AB⊥CD.
∵AB⊥CD
如果AB⊥CD,那么所得的四个角中,
必有一个是直角.
A
B
C
D
O
3.垂直的书写形式:
(已知)
(已知)
(垂直的定义)
(垂直的定义)
∴AB⊥CD
反过来:
∴∠AOC=90°
如图,已知OA⊥OB,OC⊥OD,∠AOC=27°48',求∠BOD 的度数
27°
∠BOD=360°-∠AOB-∠COD-∠AOC=152°48'=152.2°.
1.落.
2.画.
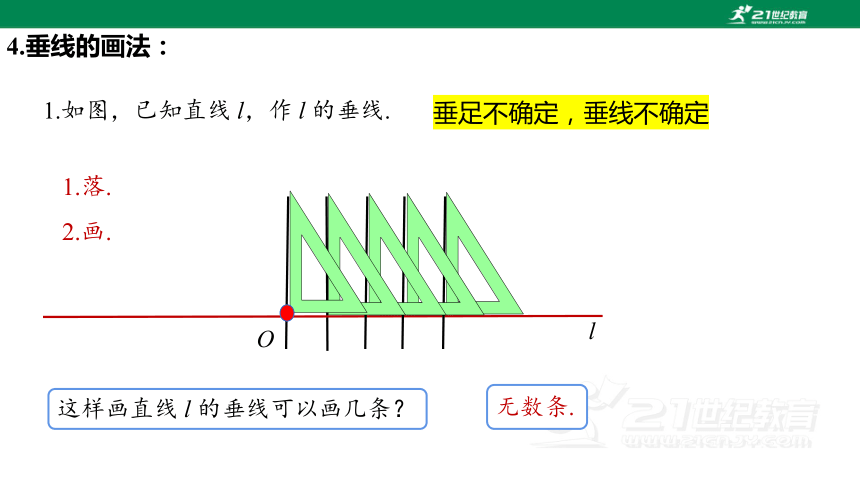
1.如图,已知直线 l,作 l 的垂线.
l
O
这样画直线 l 的垂线可以画几条?
无数条.
4.垂线的画法:
垂足不确定,垂线不确定
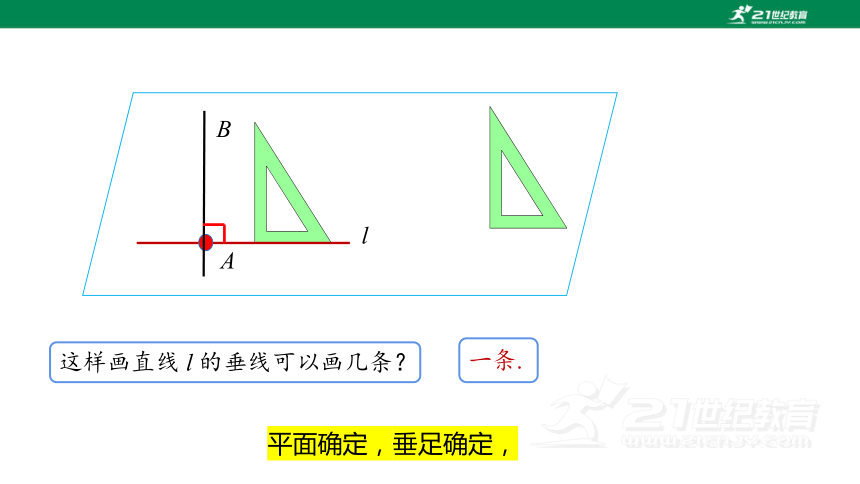
这样画直线 l 的垂线可以画几条?
一条.
平面确定,垂足确定,
l
A
B
这样画直线 l 的垂线可以画几条?
一条.
平面确定,垂足确定,
l
A
B
垂线的基本事实:
在同一平面内,过一点有且只有一条直线垂直于已知直线.
特别地,两条线段互相垂直是指这两条线段所在的直线互相垂直.
A
B
C
D
画线段的垂线,就是画它们所在直线的垂线,
垂足可能在线段上,也可能在线段的延长线上.
A
B
C
D
画射线的垂线,就是画它们所在直线的垂线,
垂足可能在射线上,也可能在射线的反向延长线上.
两条射线互相垂直是指这两条射线所在的直线互相垂直.
已知直线AB,CB,l 在同一平面内,
若AB⊥l,垂足为B,CB⊥l,垂足也为B,
则符合题意的图形可以是下图中的( )
A B C D
C
垂线的基本事实:在同一平面内,过一点有且只有一条直线与已知直线垂直,
A,B,C 三点共线.
P
A
o
C
m
D
线段PO:点P到直线AB的 .
垂线段
线段PA、PC、PD:点P到直线AB的 .
斜线段
PO斜大于直
垂线段
斜线段
A
B
P
0
C
D
E
F
以P点为圆心,线段PO长度为半径画圆.
直线外一点与直线上各点连接的所有线段中,垂线段最短.
简单说成:垂线段最短.
从直线外一点到这条直线所画垂线段的长度叫做这点到直线的距离.
垂线段PO的长度:
点P到直线AB的距离.
如图,是一个同学跳远的位置,跳远成绩怎么表示
m
过P点作PA⊥m于点A,
P
A
垂线段PA的长度就是该同学的跳远成绩.
线段PO的长度叫做点P到直线l的距离.
直线外一点与直线上各点连接的所有线段中,垂线段最短。
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。
简单说成:垂线段最短.
垂线的基本事实:在同一平面内,过一点有且只有一条直线与已知直线垂直,
B
C
A
O
1.如图,BO⊥AO,∠BOC=35°,那么∠COA=__________ ,
55°
∵∠COA=90°-∠BOC
=90° 35°=55°.
解:∵ BO⊥A0,
∴∠AOB=90°(垂直的定义).
夯实基础,稳扎稳打
2. 如图,点P在直线AB上,点C,D在直线AB的上方,且PC⊥PD,∠APC=28°,则∠BPD的度数为( )
A. 28°
B. 60°
C. 62°
D. 152°
C
∵∠BPD=180°-∠APC-∠CPD
=180°-28° 90°=62°.
解:∵ PC⊥PD,
∴∠CPD=90°(垂直的定义).
3.如图,CO⊥AB,垂足为点O,DE平分∠COB,
则∠EOB的度数为( ).
A.120° B.130° C.135° D.140°
O
C
A
B
D
E
C
4.如图AB⊥CD垂足为O,∠COF=56°, 求∠AOE
解:∵AB⊥CD
F
E
D
C
B
A
O
56°
(已知)
(垂直的定义)
(对顶角相等)
∴∠COB=90°
∴∠BOF= ∠COB-∠COF
=90°-56°=34°
∴ ∠AOE=∠BOF=34°
5.如图 ,直线AB,CD相交于O,∠AOC=35°,OE⊥CD,垂足为 O,求∠DOB,∠BOE的度数.
A
E
C
O
B
D
∴∠EOD=90°.
解:
∵∠AOC=35°,
∴ ∠DOB=∠AOC=35°.
(对顶角相等)
∵OE⊥CD,
(已知)
(垂直的定义)
∴∠BOE=
∠EOD-∠DOB
=90°-35°
=55°.
6.如图,在三角形ABC 中,∠ACB=90°,CD⊥ AB,垂足为D.
若AC=4 cm,BC=3 cm,AB=5 cm,
则点A 到直线BC 的距离为______cm,
点B 到直线AC 的距离为______cm,
点C 到直线AB的距离为______cm.
AC·BC=AB ·CD
CD=2.4 cm.
垂线段的长度表示点到直线的距离,其实质是点与垂足两点间的距离
4
3
2.4
连续递推,豁然开朗
导引:要判断OE,OF 是什么位置关系,
其实质是说明OE,OF 是否垂直,
即要看∠EOF 是否为90°;要让∠EOF=90°,
需说明∠EOF=∠AOC 或∠EOF=∠BOC 都可,
这样就把问题转化为说明∠AOE=∠COF (已知)了.
7. 如图,CO⊥AB 于点O,∠AOE=∠COF,
则射线OE,OF 是什么位置关系?请说明理由.
解:射线OE,OF 互相垂直.理由如下:
∵ CO⊥AB,∴ ∠AOC=90°.
∵ ∠AOE=∠COF,
∴∠AOE+∠COE=∠COF+∠COE,
即∠AOC=∠EOF=90°. ∴ OE 与OF 互相垂直(垂直定义).
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.1 直线的相交(2)
浙教版七年级下册
两条直线相交的一种特殊情况:两条直线互相垂直
如图,当∠AOC=90°时,
∠BOD、∠AOD、∠BOC等于多少度?为什么?
A
B
C
D
O
∠BOD=90°
∠AOD=90°
∠BOC=90°
1.垂线的定义:当两条直线相交所成的四个角中,如果有一个角是 ,
其他三个角也都为 ,此时,这两条直线 .
其中一条直线叫做另一条直线的 .交点叫做 .
直角
互相垂直
垂线
垂足
直角
b
a
O
a、b互相垂直,O叫垂足.
a叫b的垂线,b也叫a的垂线.
垂足
b
a
O
2.垂直的表示:
① a⊥b,
垂足为O.
② b⊥a,
垂足为O.
F
E
M
N
O
MN⊥EF ,垂足为O.
A
B
O
E
① AB⊥OE,垂足为O.
∵∠AOC=90°
如果直线AB、CD 相交于点O,∠AOC=90°,那么 AB⊥CD.
∵AB⊥CD
如果AB⊥CD,那么所得的四个角中,
必有一个是直角.
A
B
C
D
O
3.垂直的书写形式:
(已知)
(已知)
(垂直的定义)
(垂直的定义)
∴AB⊥CD
反过来:
∴∠AOC=90°
如图,已知OA⊥OB,OC⊥OD,∠AOC=27°48',求∠BOD 的度数
27°
∠BOD=360°-∠AOB-∠COD-∠AOC=152°48'=152.2°.
1.落.
2.画.
1.如图,已知直线 l,作 l 的垂线.
l
O
这样画直线 l 的垂线可以画几条?
无数条.
4.垂线的画法:
垂足不确定,垂线不确定
这样画直线 l 的垂线可以画几条?
一条.
平面确定,垂足确定,
l
A
B
这样画直线 l 的垂线可以画几条?
一条.
平面确定,垂足确定,
l
A
B
垂线的基本事实:
在同一平面内,过一点有且只有一条直线垂直于已知直线.
特别地,两条线段互相垂直是指这两条线段所在的直线互相垂直.
A
B
C
D
画线段的垂线,就是画它们所在直线的垂线,
垂足可能在线段上,也可能在线段的延长线上.
A
B
C
D
画射线的垂线,就是画它们所在直线的垂线,
垂足可能在射线上,也可能在射线的反向延长线上.
两条射线互相垂直是指这两条射线所在的直线互相垂直.
已知直线AB,CB,l 在同一平面内,
若AB⊥l,垂足为B,CB⊥l,垂足也为B,
则符合题意的图形可以是下图中的( )
A B C D
C
垂线的基本事实:在同一平面内,过一点有且只有一条直线与已知直线垂直,
A,B,C 三点共线.
P
A
o
C
m
D
线段PO:点P到直线AB的 .
垂线段
线段PA、PC、PD:点P到直线AB的 .
斜线段
PO
垂线段
斜线段
A
B
P
0
C
D
E
F
以P点为圆心,线段PO长度为半径画圆.
直线外一点与直线上各点连接的所有线段中,垂线段最短.
简单说成:垂线段最短.
从直线外一点到这条直线所画垂线段的长度叫做这点到直线的距离.
垂线段PO的长度:
点P到直线AB的距离.
如图,是一个同学跳远的位置,跳远成绩怎么表示
m
过P点作PA⊥m于点A,
P
A
垂线段PA的长度就是该同学的跳远成绩.
线段PO的长度叫做点P到直线l的距离.
直线外一点与直线上各点连接的所有线段中,垂线段最短。
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。
简单说成:垂线段最短.
垂线的基本事实:在同一平面内,过一点有且只有一条直线与已知直线垂直,
B
C
A
O
1.如图,BO⊥AO,∠BOC=35°,那么∠COA=__________ ,
55°
∵∠COA=90°-∠BOC
=90° 35°=55°.
解:∵ BO⊥A0,
∴∠AOB=90°(垂直的定义).
夯实基础,稳扎稳打
2. 如图,点P在直线AB上,点C,D在直线AB的上方,且PC⊥PD,∠APC=28°,则∠BPD的度数为( )
A. 28°
B. 60°
C. 62°
D. 152°
C
∵∠BPD=180°-∠APC-∠CPD
=180°-28° 90°=62°.
解:∵ PC⊥PD,
∴∠CPD=90°(垂直的定义).
3.如图,CO⊥AB,垂足为点O,DE平分∠COB,
则∠EOB的度数为( ).
A.120° B.130° C.135° D.140°
O
C
A
B
D
E
C
4.如图AB⊥CD垂足为O,∠COF=56°, 求∠AOE
解:∵AB⊥CD
F
E
D
C
B
A
O
56°
(已知)
(垂直的定义)
(对顶角相等)
∴∠COB=90°
∴∠BOF= ∠COB-∠COF
=90°-56°=34°
∴ ∠AOE=∠BOF=34°
5.如图 ,直线AB,CD相交于O,∠AOC=35°,OE⊥CD,垂足为 O,求∠DOB,∠BOE的度数.
A
E
C
O
B
D
∴∠EOD=90°.
解:
∵∠AOC=35°,
∴ ∠DOB=∠AOC=35°.
(对顶角相等)
∵OE⊥CD,
(已知)
(垂直的定义)
∴∠BOE=
∠EOD-∠DOB
=90°-35°
=55°.
6.如图,在三角形ABC 中,∠ACB=90°,CD⊥ AB,垂足为D.
若AC=4 cm,BC=3 cm,AB=5 cm,
则点A 到直线BC 的距离为______cm,
点B 到直线AC 的距离为______cm,
点C 到直线AB的距离为______cm.
AC·BC=AB ·CD
CD=2.4 cm.
垂线段的长度表示点到直线的距离,其实质是点与垂足两点间的距离
4
3
2.4
连续递推,豁然开朗
导引:要判断OE,OF 是什么位置关系,
其实质是说明OE,OF 是否垂直,
即要看∠EOF 是否为90°;要让∠EOF=90°,
需说明∠EOF=∠AOC 或∠EOF=∠BOC 都可,
这样就把问题转化为说明∠AOE=∠COF (已知)了.
7. 如图,CO⊥AB 于点O,∠AOE=∠COF,
则射线OE,OF 是什么位置关系?请说明理由.
解:射线OE,OF 互相垂直.理由如下:
∵ CO⊥AB,∴ ∠AOC=90°.
∵ ∠AOE=∠COF,
∴∠AOE+∠COE=∠COF+∠COE,
即∠AOC=∠EOF=90°. ∴ OE 与OF 互相垂直(垂直定义).
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
