1.4 平行线的判定 (1) 课件(共40张PPT)
文档属性
| 名称 | 1.4 平行线的判定 (1) 课件(共40张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-14 12:45:10 | ||
图片预览




文档简介
(共40张PPT)
1.4 平行线的判定(1)
浙教版七年级下册
识别“F”,描出“F”
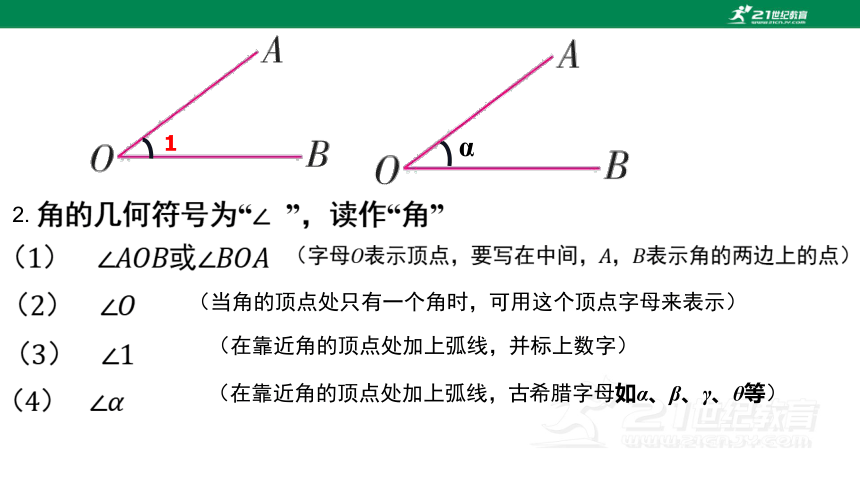
1.角是由两条有公共端点的射线所组成的图形。
这个公共端点叫做这个角的顶点
这两条射线叫做这个角的边
顶点
边
边
(当角的顶点处只有一个角时,可用这个顶点字母来表示)
(在靠近角的顶点处加上弧线,古希腊字母如α、β、γ、θ等)
(在靠近角的顶点处加上弧线,并标上数字)
α
1
2.
3.角度制:1°= , 1′= ,
60′
60″
1′= ( ) °, 1 ″= ( ) ′
180°= 179° 60′= 179° 59′ 60″
90°= 89° 60′= 89° 59′ 60″
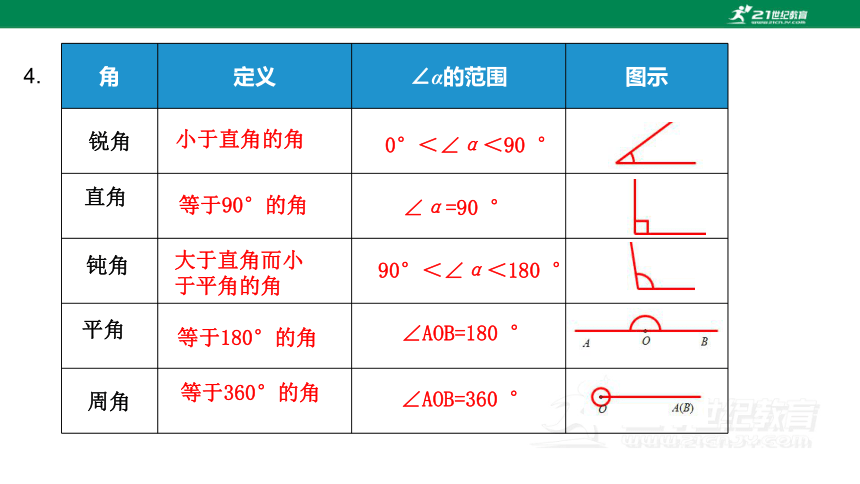
角 定义 ∠α的范围 图示
小于直角的角
等于90°的角
大于直角而小于平角的角
等于180°的角
等于360°的角
0°<∠α<90 °
∠α=90 °
90°<∠α<180 °
∠AOB=180 °
∠AOB=360 °
锐角
直角
钝角
平角
周角
4.
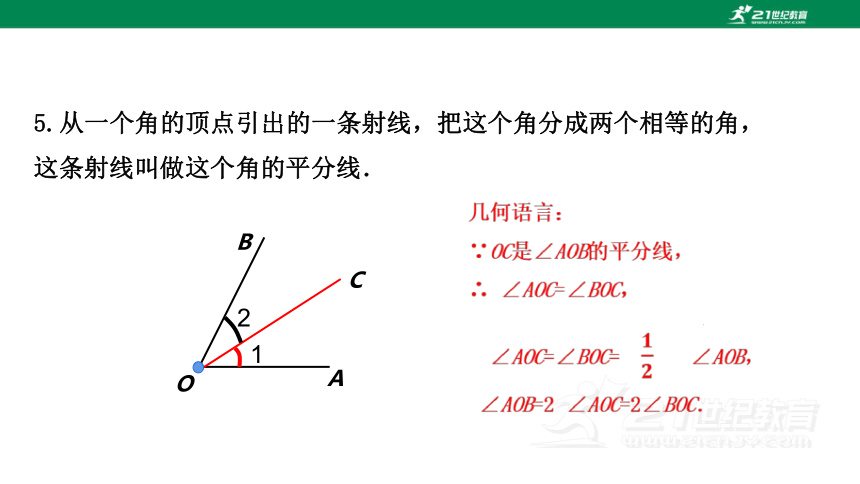
5.从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线.
O
B
A
C
1
2
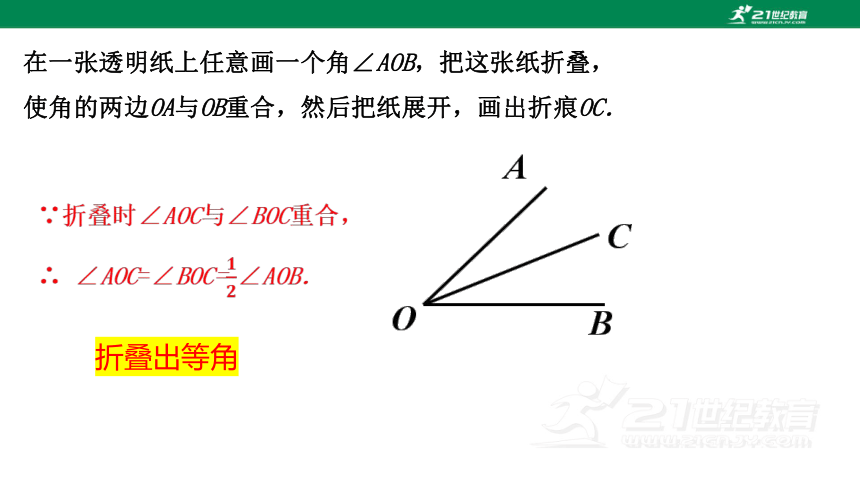
在一张透明纸上任意画一个角∠AOB,把这张纸折叠,
使角的两边OA与OB重合,然后把纸展开,画出折痕OC.
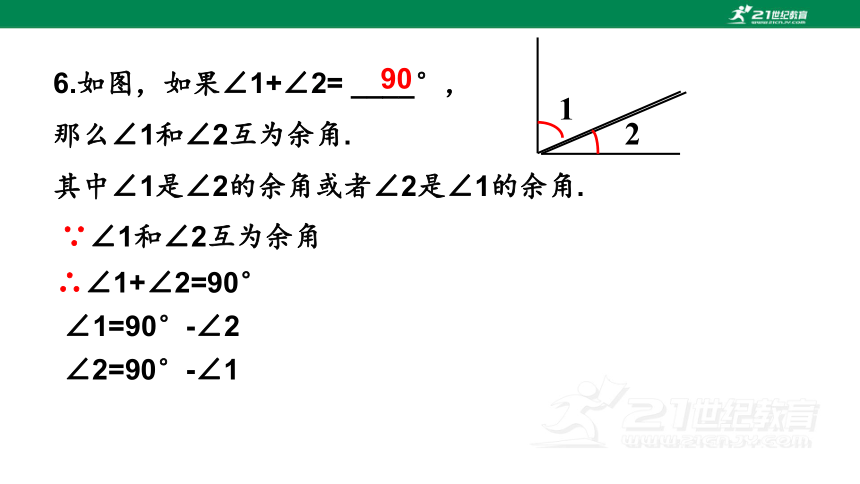
6.如图,如果∠1+∠2= ____°,
那么∠1和∠2互为余角.
其中∠1是∠2的余角或者∠2是∠1的余角.
∵∠1和∠2互为余角
∴∠1+∠2=90°
∠1=90°-∠2
∠2=90°-∠1
90
1
2
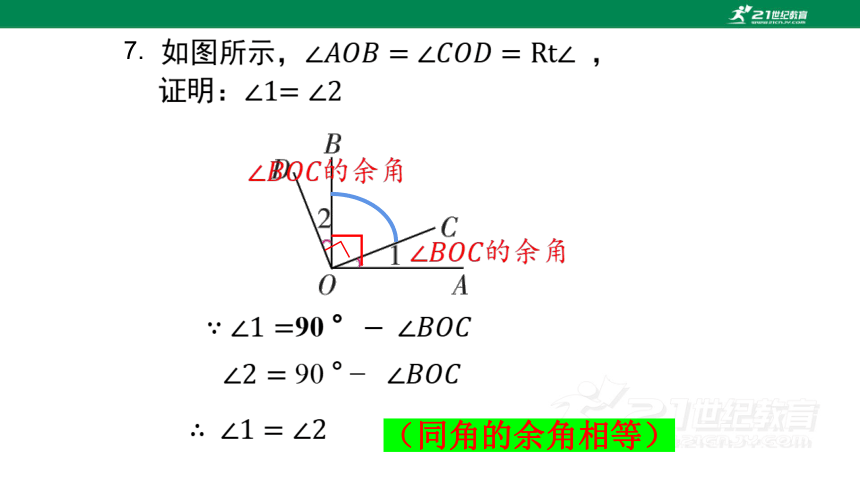
7.
∟
∟
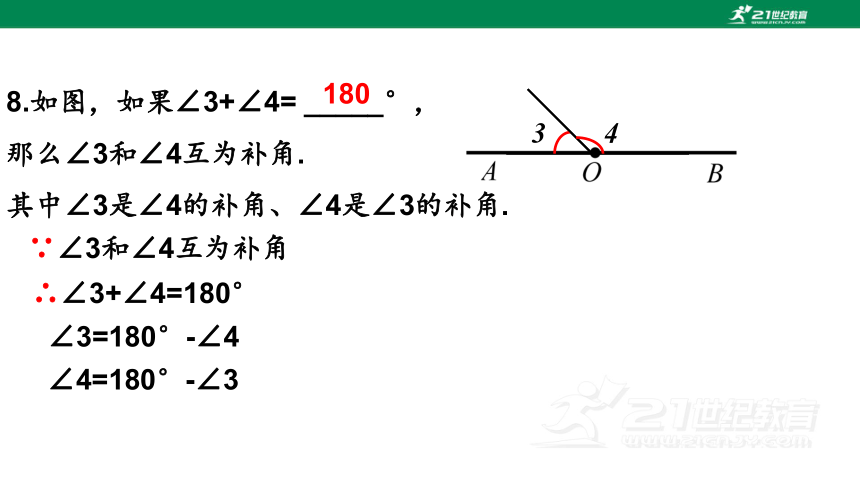
8.如图,如果∠3+∠4= _____°,
那么∠3和∠4互为补角.
其中∠3是∠4的补角、∠4是∠3的补角.
∵∠3和∠4互为补角
∴∠3+∠4=180°
∠3=180°-∠4
∠4=180°-∠3
180
3
4
9.
A
B
C
D
O
1
2
3
4
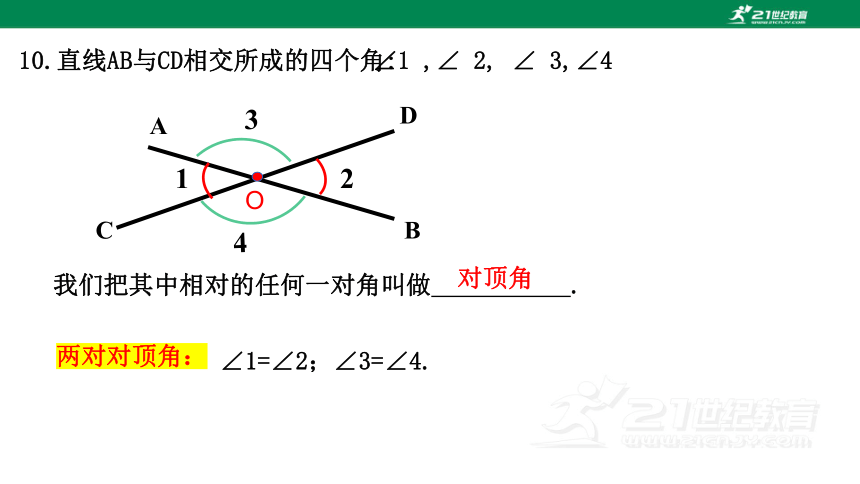
10.直线AB与CD相交所成的四个角:
∠1 ,∠ 2, ∠ 3,∠4
我们把其中相对的任何一对角叫做 .
对顶角
∠1=∠2;∠3=∠4.
1
2
3
4
A
B
C
D
O
11.如果两个角有一条公共边,它们的另一边互为_________,
那么这两个角互为邻补角.
反向延长线
∠1=180°-∠2、∠2=180°-∠1
∠2=180°-∠3、∠3=180°-∠2
∠3=180°-∠4、∠4=180°-∠3
∠4=180°-∠1、∠1=180°-∠4
∵∠AOC=90°
12.如果直线AB、CD 相交于点O,∠AOC=90°,
那么 AB⊥CD.
∵AB⊥CD
如果AB⊥CD,那么所得的四个角中,
必有一个是直角.
A
B
C
D
O
(已知)
(已知)
(垂直的定义)
(垂直的定义)
∴AB⊥CD
∴∠AOC=90°
13.直线a、b被直线 c所截构成的8个角中
4对同位角:∠1与∠5;
1
4
5
8
b
a
2
1
4
3
6
5
8
7
c
8
4
1
5
2
6
3
7
F
∠2与∠6;
∠4与∠8;
∠3与∠7.
直线a、b被直线 c所截构成的8个角中
2对内错角:∠3与∠5;
1
4
5
8
b
a
2
1
4
3
6
5
8
7
c
5
3
4
6
Z
∠4与∠6.
直线a、b被直线 c所截构成的8个角中
2对同旁内角: ∠4与∠5;
1
4
5
8
b
a
2
1
4
3
6
5
8
7
c
3
6
4
5
U
∠3与∠6.
x
x
y
y
x+x+y+y=180
∠GEF=x+y=90°,
P
450
450
判断两直线平行的基本事实:
两条直线被第三条直线所截,
如果同位角相等,
那么这两条直线平行.
同位角相等,两直线平行.
几何表达:
∵∠1=∠2
∴a∥b
(同位角相等,两直线平行)
3
4
6
5
8
7
如图,三根木条相交成∠1,∠2,固定木条b、c,
转动木条a,∠1,∠2满足什么条件时,直线a与b平行.
当∠1=∠2时,
a∥b
(同位角相等,两直线平行)
∵∠2=∠3,
∴ ∥ ;
EF
GH
∵∠1=∠2,
∴ ∥ ;
AB
CD
b
c
a
d
66°
66°
67°
b
c
a
d
66°
66°
67°
∴b c
∴a d
C
A
D
B
E
F
∵∠ADE=∠ABC,
∴__∥ __
∵∠ACD=∠F,
∴__∥ __
∵∠DEC=∠BCF,
∴__∥ __
DE
BC
CD
BF
DE
BC
C
A
D
B
E
F
C
A
D
B
E
F
解:∵∠2+∠3=180°且∠2=∠135°
∴∠3=180°- 135°=45°
∵∠1=45°
∴∠1=∠3
∴l1//l2(同位角相等,两直线平行)
已知直线 被 所截,如图,
试判断 与 是否平行.并说明理由.
变1:条件弱化为∠1+∠2=180°,结论是否仍然成立?
4
变2:条件变为∠1=∠4,结论是否仍然成立?请说明理由.
变式2:
解:∵∠3=∠4(对顶角相等)
∵∠1=∠4
∴∠1=∠3
∴l1//l2(同位角相等,两直线平行)
变式1:
解:∵∠2+∠3=180°
∵∠1+∠2=180°
∴∠1=∠3
∴l1//l2(同位角相等,两直线平行)
若∠1=45°
,∠2=135
善思者,变!
如图,AB⊥EF,CD⊥EF,E,F分别为垂足.
直线AB与CD平行吗?请说明理由.
解
∵ AB⊥EF,CD⊥EF,
∴ ∠1=∠2=Rt∠.
∴ AB∥CD
(同位角相等,两直线平行.)
A
B
C
D
E
F
“在同一平面 ,垂直于同一条直线的两条直线互相平行”.
2
1
由一般到特殊
1
2
∵l1⊥l3,l2⊥l3,
∴ l1 ∥ l2
∵∠1=∠2
∴ l1 ∥ l2
如图,木工师傅用角尺画出工件边缘的两条垂线,
则这两条垂线就平行了.为什么呢
1
2
(在同一平面内,垂直于同一条直线的两条直线互相平行)
.
A
D
E
B
C
32
32°
夯实基础,稳扎稳打
2.工人师傅在路口画上了斑马线,他们想检验斑马线是否平行,你能帮助他们吗?请你设计一个方案来检验斑马线是否平行.
方案一:斜方向构造一条截线,
使他们构成同位角,然后再检验这些同位角是否相等.
方案二:垂直方向构造一条截线,然后检验各同位角是否是直角.
生活中的数学
因为吊索同时垂直于经过吊索与桥面交点的直线,所以它们互相平行。
依据:在同一平面内,垂直于同一直线的两直线平行。
3
4. 某人骑自行车从 A 地出发,沿正东方向前进至 B 处后,右转 15°,
沿直线向前行驶到C处(如图).若他想仍按正东方向,
请画出他应怎样调整行驶的路线 说明理由.
解: 向左拐 15°.
(同位角相等,两直线平行).
∵∠1=∠2=15°
∴AB//CD
5 . 如图,已知直线 AD,BE被直线AB所截,AC ⊥BE于点C.若∠1=50°,∠2=40 °则AD与 BE平行吗 请说明理由.
A
B
1
2
C
D
E
(第2题)
F
∵∠FAD=∠FCE=90°
∴AD//BE
∵ AD⊥CF,BE⊥CF,
∴AD//BE
6. 如图,AB⊥CD于点B,AE与BF相交于点G,且FGE=60°,∠ABG=30°.判段AE与CD是否平行?
∵∠FGE=∠FBD=60°
∴AE//CD
7.画一画:已知直线AB和直线外一点C(如图).你能用一把三角尺过点C画AB的平行线吗?如果能,说明方法,并画出图形.
A
B
C
E
如图,直线CE就是所求的平行线.
D
连续递推,豁然开朗
(在同一平面内,垂直于同一条直线的两条直线互相平行)
8.如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,
∠2=45°,要使直线b与直线c平行,可将直线b绕点A逆时针旋转( ) A.15° B. 30° C. 45° D. 60°
A
45°
120°
9.如图,已知∠ABD=∠ACE,BF、CG分别是∠ABD、∠ACE的平分线,证明:BF∥CG
A
B
C
D
E
F
G
证明:
1
2
∵BF、CG分别是∠ABD、∠ACE的平分线
∴ ∠1= ∠ABD,∠2= ∠ACE
∵
∠ABD=∠ACE
∴ ∠1=∠2
∴
BF∥CG( )
同位角相等,两直线平行
小李的解答如下:
∵ ∠1=∠2,
∴ AB∥CD(同位角相等两直线平行)
请你再添加一个条件,使AB∥CD,并说明理由.
10.如图,点B、D在直线MN上,已知∠1=∠2,请你判断AB、CD是否平行,并说明理由.
(1)∠ABM=∠CDM
(2)∠EBM=∠FDM
1
2
A
B
D
C
M
N
E
F
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.4 平行线的判定(1)
浙教版七年级下册
识别“F”,描出“F”
1.角是由两条有公共端点的射线所组成的图形。
这个公共端点叫做这个角的顶点
这两条射线叫做这个角的边
顶点
边
边
(当角的顶点处只有一个角时,可用这个顶点字母来表示)
(在靠近角的顶点处加上弧线,古希腊字母如α、β、γ、θ等)
(在靠近角的顶点处加上弧线,并标上数字)
α
1
2.
3.角度制:1°= , 1′= ,
60′
60″
1′= ( ) °, 1 ″= ( ) ′
180°= 179° 60′= 179° 59′ 60″
90°= 89° 60′= 89° 59′ 60″
角 定义 ∠α的范围 图示
小于直角的角
等于90°的角
大于直角而小于平角的角
等于180°的角
等于360°的角
0°<∠α<90 °
∠α=90 °
90°<∠α<180 °
∠AOB=180 °
∠AOB=360 °
锐角
直角
钝角
平角
周角
4.
5.从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线.
O
B
A
C
1
2
在一张透明纸上任意画一个角∠AOB,把这张纸折叠,
使角的两边OA与OB重合,然后把纸展开,画出折痕OC.
6.如图,如果∠1+∠2= ____°,
那么∠1和∠2互为余角.
其中∠1是∠2的余角或者∠2是∠1的余角.
∵∠1和∠2互为余角
∴∠1+∠2=90°
∠1=90°-∠2
∠2=90°-∠1
90
1
2
7.
∟
∟
8.如图,如果∠3+∠4= _____°,
那么∠3和∠4互为补角.
其中∠3是∠4的补角、∠4是∠3的补角.
∵∠3和∠4互为补角
∴∠3+∠4=180°
∠3=180°-∠4
∠4=180°-∠3
180
3
4
9.
A
B
C
D
O
1
2
3
4
10.直线AB与CD相交所成的四个角:
∠1 ,∠ 2, ∠ 3,∠4
我们把其中相对的任何一对角叫做 .
对顶角
∠1=∠2;∠3=∠4.
1
2
3
4
A
B
C
D
O
11.如果两个角有一条公共边,它们的另一边互为_________,
那么这两个角互为邻补角.
反向延长线
∠1=180°-∠2、∠2=180°-∠1
∠2=180°-∠3、∠3=180°-∠2
∠3=180°-∠4、∠4=180°-∠3
∠4=180°-∠1、∠1=180°-∠4
∵∠AOC=90°
12.如果直线AB、CD 相交于点O,∠AOC=90°,
那么 AB⊥CD.
∵AB⊥CD
如果AB⊥CD,那么所得的四个角中,
必有一个是直角.
A
B
C
D
O
(已知)
(已知)
(垂直的定义)
(垂直的定义)
∴AB⊥CD
∴∠AOC=90°
13.直线a、b被直线 c所截构成的8个角中
4对同位角:∠1与∠5;
1
4
5
8
b
a
2
1
4
3
6
5
8
7
c
8
4
1
5
2
6
3
7
F
∠2与∠6;
∠4与∠8;
∠3与∠7.
直线a、b被直线 c所截构成的8个角中
2对内错角:∠3与∠5;
1
4
5
8
b
a
2
1
4
3
6
5
8
7
c
5
3
4
6
Z
∠4与∠6.
直线a、b被直线 c所截构成的8个角中
2对同旁内角: ∠4与∠5;
1
4
5
8
b
a
2
1
4
3
6
5
8
7
c
3
6
4
5
U
∠3与∠6.
x
x
y
y
x+x+y+y=180
∠GEF=x+y=90°,
P
450
450
判断两直线平行的基本事实:
两条直线被第三条直线所截,
如果同位角相等,
那么这两条直线平行.
同位角相等,两直线平行.
几何表达:
∵∠1=∠2
∴a∥b
(同位角相等,两直线平行)
3
4
6
5
8
7
如图,三根木条相交成∠1,∠2,固定木条b、c,
转动木条a,∠1,∠2满足什么条件时,直线a与b平行.
当∠1=∠2时,
a∥b
(同位角相等,两直线平行)
∵∠2=∠3,
∴ ∥ ;
EF
GH
∵∠1=∠2,
∴ ∥ ;
AB
CD
b
c
a
d
66°
66°
67°
b
c
a
d
66°
66°
67°
∴b c
∴a d
C
A
D
B
E
F
∵∠ADE=∠ABC,
∴__∥ __
∵∠ACD=∠F,
∴__∥ __
∵∠DEC=∠BCF,
∴__∥ __
DE
BC
CD
BF
DE
BC
C
A
D
B
E
F
C
A
D
B
E
F
解:∵∠2+∠3=180°且∠2=∠135°
∴∠3=180°- 135°=45°
∵∠1=45°
∴∠1=∠3
∴l1//l2(同位角相等,两直线平行)
已知直线 被 所截,如图,
试判断 与 是否平行.并说明理由.
变1:条件弱化为∠1+∠2=180°,结论是否仍然成立?
4
变2:条件变为∠1=∠4,结论是否仍然成立?请说明理由.
变式2:
解:∵∠3=∠4(对顶角相等)
∵∠1=∠4
∴∠1=∠3
∴l1//l2(同位角相等,两直线平行)
变式1:
解:∵∠2+∠3=180°
∵∠1+∠2=180°
∴∠1=∠3
∴l1//l2(同位角相等,两直线平行)
若∠1=45°
,∠2=135
善思者,变!
如图,AB⊥EF,CD⊥EF,E,F分别为垂足.
直线AB与CD平行吗?请说明理由.
解
∵ AB⊥EF,CD⊥EF,
∴ ∠1=∠2=Rt∠.
∴ AB∥CD
(同位角相等,两直线平行.)
A
B
C
D
E
F
“在同一平面 ,垂直于同一条直线的两条直线互相平行”.
2
1
由一般到特殊
1
2
∵l1⊥l3,l2⊥l3,
∴ l1 ∥ l2
∵∠1=∠2
∴ l1 ∥ l2
如图,木工师傅用角尺画出工件边缘的两条垂线,
则这两条垂线就平行了.为什么呢
1
2
(在同一平面内,垂直于同一条直线的两条直线互相平行)
.
A
D
E
B
C
32
32°
夯实基础,稳扎稳打
2.工人师傅在路口画上了斑马线,他们想检验斑马线是否平行,你能帮助他们吗?请你设计一个方案来检验斑马线是否平行.
方案一:斜方向构造一条截线,
使他们构成同位角,然后再检验这些同位角是否相等.
方案二:垂直方向构造一条截线,然后检验各同位角是否是直角.
生活中的数学
因为吊索同时垂直于经过吊索与桥面交点的直线,所以它们互相平行。
依据:在同一平面内,垂直于同一直线的两直线平行。
3
4. 某人骑自行车从 A 地出发,沿正东方向前进至 B 处后,右转 15°,
沿直线向前行驶到C处(如图).若他想仍按正东方向,
请画出他应怎样调整行驶的路线 说明理由.
解: 向左拐 15°.
(同位角相等,两直线平行).
∵∠1=∠2=15°
∴AB//CD
5 . 如图,已知直线 AD,BE被直线AB所截,AC ⊥BE于点C.若∠1=50°,∠2=40 °则AD与 BE平行吗 请说明理由.
A
B
1
2
C
D
E
(第2题)
F
∵∠FAD=∠FCE=90°
∴AD//BE
∵ AD⊥CF,BE⊥CF,
∴AD//BE
6. 如图,AB⊥CD于点B,AE与BF相交于点G,且FGE=60°,∠ABG=30°.判段AE与CD是否平行?
∵∠FGE=∠FBD=60°
∴AE//CD
7.画一画:已知直线AB和直线外一点C(如图).你能用一把三角尺过点C画AB的平行线吗?如果能,说明方法,并画出图形.
A
B
C
E
如图,直线CE就是所求的平行线.
D
连续递推,豁然开朗
(在同一平面内,垂直于同一条直线的两条直线互相平行)
8.如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,
∠2=45°,要使直线b与直线c平行,可将直线b绕点A逆时针旋转( ) A.15° B. 30° C. 45° D. 60°
A
45°
120°
9.如图,已知∠ABD=∠ACE,BF、CG分别是∠ABD、∠ACE的平分线,证明:BF∥CG
A
B
C
D
E
F
G
证明:
1
2
∵BF、CG分别是∠ABD、∠ACE的平分线
∴ ∠1= ∠ABD,∠2= ∠ACE
∵
∠ABD=∠ACE
∴ ∠1=∠2
∴
BF∥CG( )
同位角相等,两直线平行
小李的解答如下:
∵ ∠1=∠2,
∴ AB∥CD(同位角相等两直线平行)
请你再添加一个条件,使AB∥CD,并说明理由.
10.如图,点B、D在直线MN上,已知∠1=∠2,请你判断AB、CD是否平行,并说明理由.
(1)∠ABM=∠CDM
(2)∠EBM=∠FDM
1
2
A
B
D
C
M
N
E
F
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
