1.5 平行线的性质(1) 课件(共28张PPT)
文档属性
| 名称 | 1.5 平行线的性质(1) 课件(共28张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-15 00:00:00 | ||
图片预览




文档简介
(共28张PPT)
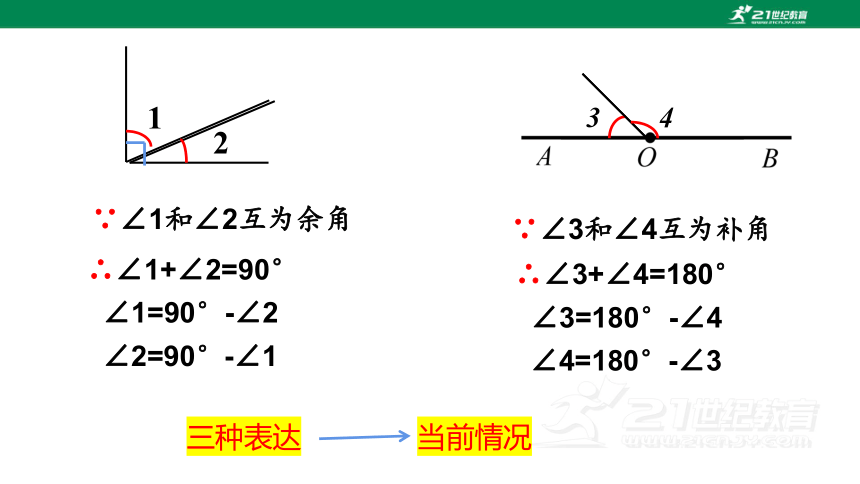
∵∠3和∠4互为补角
∴∠3+∠4=180°
∠3=180°-∠4
∠4=180°-∠3
3
4
∵∠1和∠2互为余角
∴∠1+∠2=90°
∠1=90°-∠2
∠2=90°-∠1
1
2
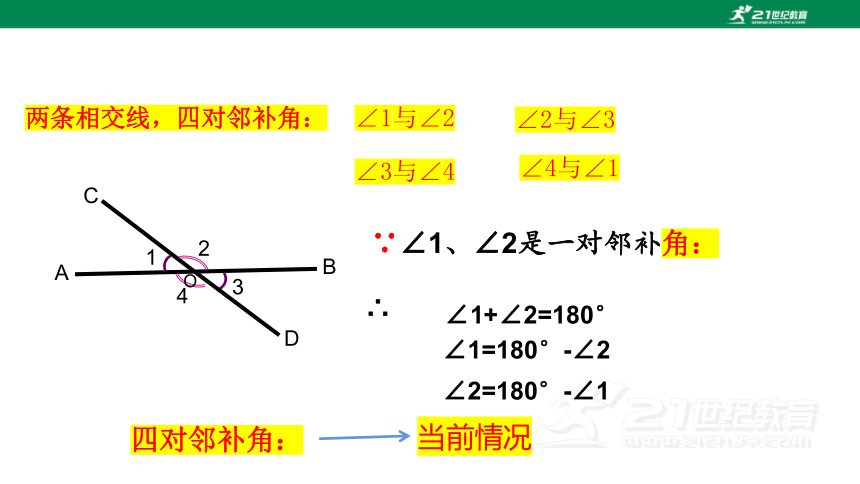
A
B
C
D
O
1
2
3
4
∠1=∠2
∠3=∠4(对顶角相等)
∠3与∠4
1
2
3
4
A
B
C
D
O
∴
∠1=180°-∠2
∠2=180°-∠1
∠1+∠2=180°
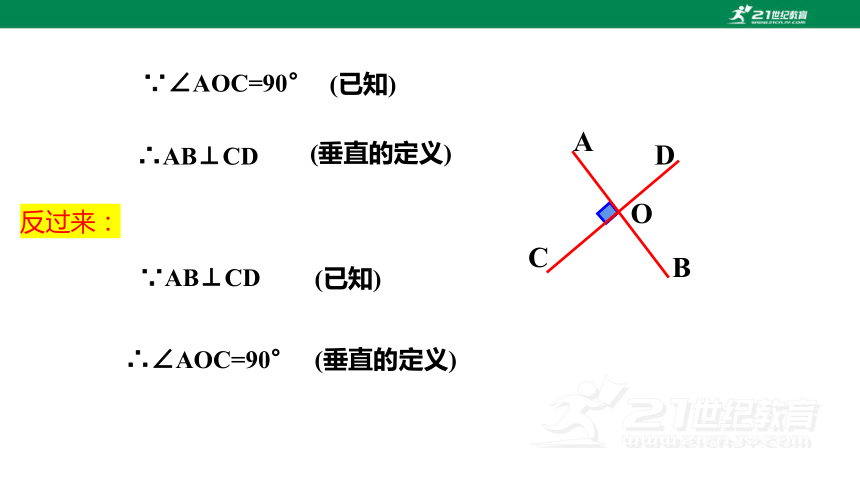
∵∠AOC=90°
∵AB⊥CD
A
B
C
D
O
(已知)
(已知)
(垂直的定义)
(垂直的定义)
∴AB⊥CD
∴∠AOC=90°
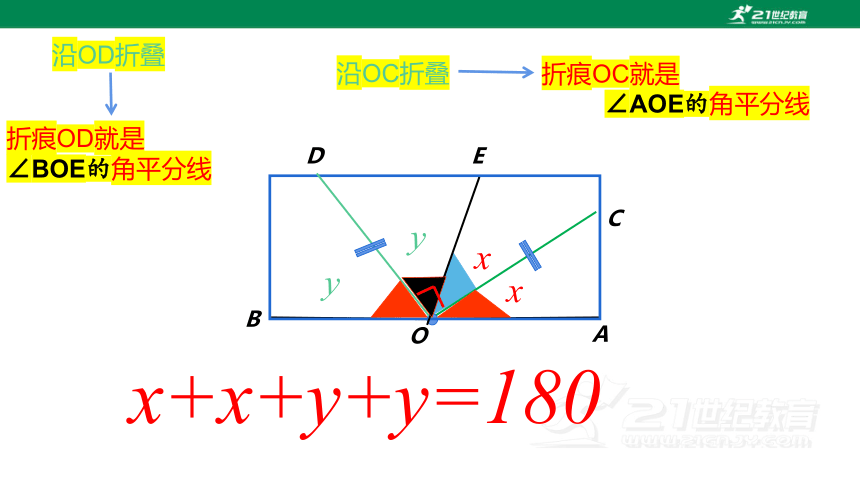
x+x+y+y=180
C
O
B
A
D
E
y
x
x
y
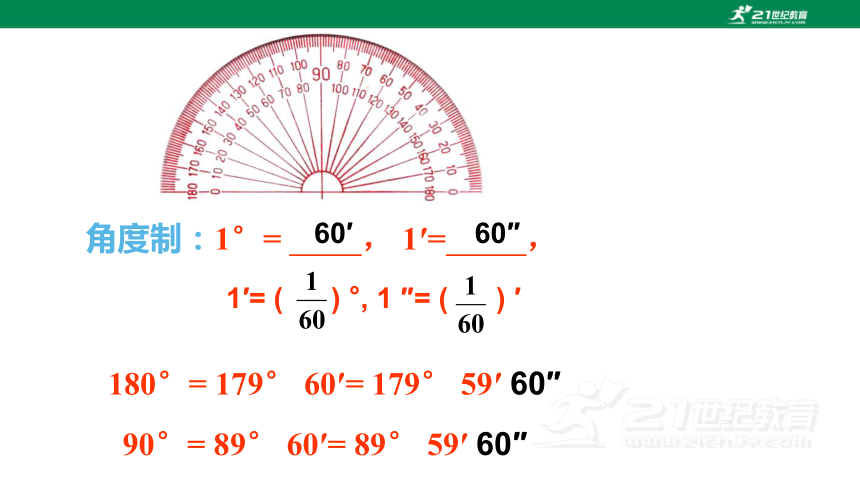
角度制:1°= , 1′= ,
60′
60″
1′= ( ) °, 1 ″= ( ) ′
180°= 179° 60′= 179° 59′ 60″
90°= 89° 60′= 89° 59′ 60″
5、垂直于同一条直线的两条直线互相平行;
6、平行于同一条直线的两条直线互相平行.
判定平行线的方法:
1、平行线的定义:在同一平面内不相交的两条直线.
2、同位角相等,两直线平行;
3、内错角相等,两直线平行;
4、同旁内角互补,两直线平行;
a
b
c
c
a
b
60°
60°
∠1=∠5
a∥b
方法一:度量法
a
c
b
5
1
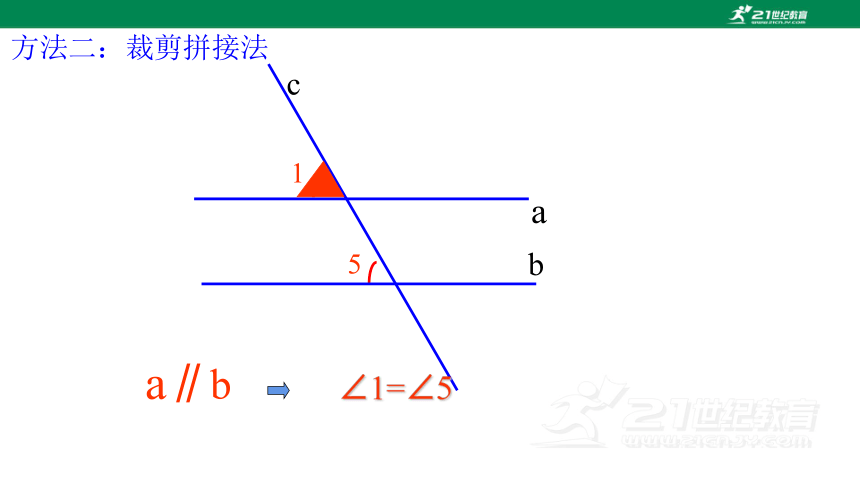
方法二:裁剪拼接法
a
c
b
5
1
∠1=∠5
a∥b
方法二:送
a
c
b
6
2
∠2=∠6
a∥b
简单地说:两直线平行,同位角相等
如果两条平行直线被第三条直线所截,同位角相等
平行线的性质一:
∵ a//b (已知)
∴ ∠1=∠5 (两直线平行,同位角相等)
a
c
b
5
1
几何表达:
a
c
b
5
1
如果直线a与b不平行,你的猜想还成立吗?
结论:如果直线a与b不平行,
则同位角不相等.
如图,放缩尺的各组对边互相平行. 图中∠α,∠β,∠γ相等吗
平行线:送角到恰当位置
θ
α
β
γ
∠α=∠β=∠γ=∠θ
例1
解
如图:梯子的各条横档互相平行,∠1=100o,求∠2的度数.
1
2
A
B
C
D
3
∵AB∥CD(已知)
∴∠3=∠1=100o
∴∠2=1800-∠3=80o
(平行线的性质)
(平角的意义)
100o
例 如图,已知∠1=∠2,若直线b⊥m,则直线a⊥m,请说明理由.
解 ∵ ∠1=∠2(已知)
∴a∥b(同位角相等,两直线平行)
∴ ∠3=∠4
( 两直线平行,同位角相等)
∵b⊥m(已知)
∴ ∠4=900( )
垂直的意义
∴ ∠3=900
∴a⊥m
n
1
2
m
a
b
3
4
条件 结论 推理思路
平行线的性质与判定的区别
平行线的性质与判定的共同前提:
平行线的
判定
同位角相等
两直线平行
角相等 线平行
平行线的
性质
两直线平行
同位角相等
线平行 角相等
两条直线被第三条直线所截
小结
判 定
性 质
由“线”定“角”
由“线”的位置关系(平行),
定“角”的数量关系(相等).
由“角”定“线”
由“角”的数量关系(相等),
定“线”的位置关系(平行).
同旁内角互补,两直线平行
1.如图,已知直线l1, l2,l3.若∠1+∠2=180°,则∠3= ∠4.
完成下面的说理过程(填空).
解:∵∠1+∠2=180°,
∴________∥________. (____________________________),
l1
l2
(两直线平行,同位角相等)
∠3= ∠4.
夯实基础,稳扎稳打
∴ (______________________),
2.如图,已知直线l1 ,l2 ,l3 ,l4.∠1=∠2,
则 ∠3=∠4.完成下面的说理过程(填空).
∵∠1=∠2,
(内错角相等,两直线平行)
1
2
3
4
两直线平行,同位角相等
l1
l2
∴____∥____.
∴ (______________________),
∠3=∠4
3.已知:如图∠AED=60°,∠C=60°,∠ADE=40°,
问∠ B等于多少度?为什么
两直线平行,同位角相等
(同位角相等,两直线平行)
60o
60o
解:∵ ∠AED=∠C=60° (已知)
DE//BC
∠ADE=∠B=40°
∴ _____________________,
∴ (______________________),
4.如图,AB∥CD,EF∥GH,试探究∠1与∠4的数量关系,并说明理由.
3
解:∠1+∠4=180°.理由如下:
∵AB∥CD,EF∥GH,
∴∠2=∠3,∠___=∠___(_________________________).
∴∠2=∠5(__________).
又∵∠4+∠5=180°, ∴∠2+∠4=180°(__________).
∵∠1=∠2(____________),
∴∠1+∠4=180°(__________).
5
两直线平行,同位角相等
等量代换
等量代换
对顶角相等
等量代换
1
2
5.如图:已知直线l1∥l2,∠1=40o,求∠2的度数.
∠2=40o
6.如图,直线a∥b,直线c分别交直线a,b于点A,B.若∠2=145°,则∠1=( )
A.45° B.35°
C.55° D.40°
B
7.如图,已知a,b,c,d四条直线.
(1)图中哪些直线互相平行?哪些直线相交?
(2)说出∠a的度数.
76°
76°
77°
a∥b
c、d 相交
∠a=77°
56o
56o
连续递推。豁然开朗
9.如图,已知AD⊥BC,FG⊥BC,垂足分别为D,G,∠1=∠2,
试猜想∠BDE与∠C的大小关系,并说明理由.
解:∠BDE=∠C.理由如下:
∵AD⊥BC,FG⊥BC,∴AD∥FG.
∴∠1=∠3.
又∵∠1=∠2,∴∠2=∠3.
∴DE∥AC. ∴∠BDE=∠C.
3
4
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
∵∠3和∠4互为补角
∴∠3+∠4=180°
∠3=180°-∠4
∠4=180°-∠3
3
4
∵∠1和∠2互为余角
∴∠1+∠2=90°
∠1=90°-∠2
∠2=90°-∠1
1
2
A
B
C
D
O
1
2
3
4
∠1=∠2
∠3=∠4(对顶角相等)
∠3与∠4
1
2
3
4
A
B
C
D
O
∴
∠1=180°-∠2
∠2=180°-∠1
∠1+∠2=180°
∵∠AOC=90°
∵AB⊥CD
A
B
C
D
O
(已知)
(已知)
(垂直的定义)
(垂直的定义)
∴AB⊥CD
∴∠AOC=90°
x+x+y+y=180
C
O
B
A
D
E
y
x
x
y
角度制:1°= , 1′= ,
60′
60″
1′= ( ) °, 1 ″= ( ) ′
180°= 179° 60′= 179° 59′ 60″
90°= 89° 60′= 89° 59′ 60″
5、垂直于同一条直线的两条直线互相平行;
6、平行于同一条直线的两条直线互相平行.
判定平行线的方法:
1、平行线的定义:在同一平面内不相交的两条直线.
2、同位角相等,两直线平行;
3、内错角相等,两直线平行;
4、同旁内角互补,两直线平行;
a
b
c
c
a
b
60°
60°
∠1=∠5
a∥b
方法一:度量法
a
c
b
5
1
方法二:裁剪拼接法
a
c
b
5
1
∠1=∠5
a∥b
方法二:送
a
c
b
6
2
∠2=∠6
a∥b
简单地说:两直线平行,同位角相等
如果两条平行直线被第三条直线所截,同位角相等
平行线的性质一:
∵ a//b (已知)
∴ ∠1=∠5 (两直线平行,同位角相等)
a
c
b
5
1
几何表达:
a
c
b
5
1
如果直线a与b不平行,你的猜想还成立吗?
结论:如果直线a与b不平行,
则同位角不相等.
如图,放缩尺的各组对边互相平行. 图中∠α,∠β,∠γ相等吗
平行线:送角到恰当位置
θ
α
β
γ
∠α=∠β=∠γ=∠θ
例1
解
如图:梯子的各条横档互相平行,∠1=100o,求∠2的度数.
1
2
A
B
C
D
3
∵AB∥CD(已知)
∴∠3=∠1=100o
∴∠2=1800-∠3=80o
(平行线的性质)
(平角的意义)
100o
例 如图,已知∠1=∠2,若直线b⊥m,则直线a⊥m,请说明理由.
解 ∵ ∠1=∠2(已知)
∴a∥b(同位角相等,两直线平行)
∴ ∠3=∠4
( 两直线平行,同位角相等)
∵b⊥m(已知)
∴ ∠4=900( )
垂直的意义
∴ ∠3=900
∴a⊥m
n
1
2
m
a
b
3
4
条件 结论 推理思路
平行线的性质与判定的区别
平行线的性质与判定的共同前提:
平行线的
判定
同位角相等
两直线平行
角相等 线平行
平行线的
性质
两直线平行
同位角相等
线平行 角相等
两条直线被第三条直线所截
小结
判 定
性 质
由“线”定“角”
由“线”的位置关系(平行),
定“角”的数量关系(相等).
由“角”定“线”
由“角”的数量关系(相等),
定“线”的位置关系(平行).
同旁内角互补,两直线平行
1.如图,已知直线l1, l2,l3.若∠1+∠2=180°,则∠3= ∠4.
完成下面的说理过程(填空).
解:∵∠1+∠2=180°,
∴________∥________. (____________________________),
l1
l2
(两直线平行,同位角相等)
∠3= ∠4.
夯实基础,稳扎稳打
∴ (______________________),
2.如图,已知直线l1 ,l2 ,l3 ,l4.∠1=∠2,
则 ∠3=∠4.完成下面的说理过程(填空).
∵∠1=∠2,
(内错角相等,两直线平行)
1
2
3
4
两直线平行,同位角相等
l1
l2
∴____∥____.
∴ (______________________),
∠3=∠4
3.已知:如图∠AED=60°,∠C=60°,∠ADE=40°,
问∠ B等于多少度?为什么
两直线平行,同位角相等
(同位角相等,两直线平行)
60o
60o
解:∵ ∠AED=∠C=60° (已知)
DE//BC
∠ADE=∠B=40°
∴ _____________________,
∴ (______________________),
4.如图,AB∥CD,EF∥GH,试探究∠1与∠4的数量关系,并说明理由.
3
解:∠1+∠4=180°.理由如下:
∵AB∥CD,EF∥GH,
∴∠2=∠3,∠___=∠___(_________________________).
∴∠2=∠5(__________).
又∵∠4+∠5=180°, ∴∠2+∠4=180°(__________).
∵∠1=∠2(____________),
∴∠1+∠4=180°(__________).
5
两直线平行,同位角相等
等量代换
等量代换
对顶角相等
等量代换
1
2
5.如图:已知直线l1∥l2,∠1=40o,求∠2的度数.
∠2=40o
6.如图,直线a∥b,直线c分别交直线a,b于点A,B.若∠2=145°,则∠1=( )
A.45° B.35°
C.55° D.40°
B
7.如图,已知a,b,c,d四条直线.
(1)图中哪些直线互相平行?哪些直线相交?
(2)说出∠a的度数.
76°
76°
77°
a∥b
c、d 相交
∠a=77°
56o
56o
连续递推。豁然开朗
9.如图,已知AD⊥BC,FG⊥BC,垂足分别为D,G,∠1=∠2,
试猜想∠BDE与∠C的大小关系,并说明理由.
解:∠BDE=∠C.理由如下:
∵AD⊥BC,FG⊥BC,∴AD∥FG.
∴∠1=∠3.
又∵∠1=∠2,∴∠2=∠3.
∴DE∥AC. ∴∠BDE=∠C.
3
4
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
