第一章 相交线与平行线 章末复习(2) 想-----一潘二推三要使
文档属性
| 名称 | 第一章 相交线与平行线 章末复习(2) 想-----一潘二推三要使 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-14 13:20:20 | ||
图片预览


文档简介
(共13张PPT)
浙教版七年级下册
第一章 相交线与平行线 章末复习
想:一判二推三要使,
写,条分缕析,分步表达
一判:
等角
F、Z
非F、Z
F、Z、u
两角互补
U
非U
F、Z、U
两角互余:
F、Z、U
等角、两角互补:
等角、两角互补:
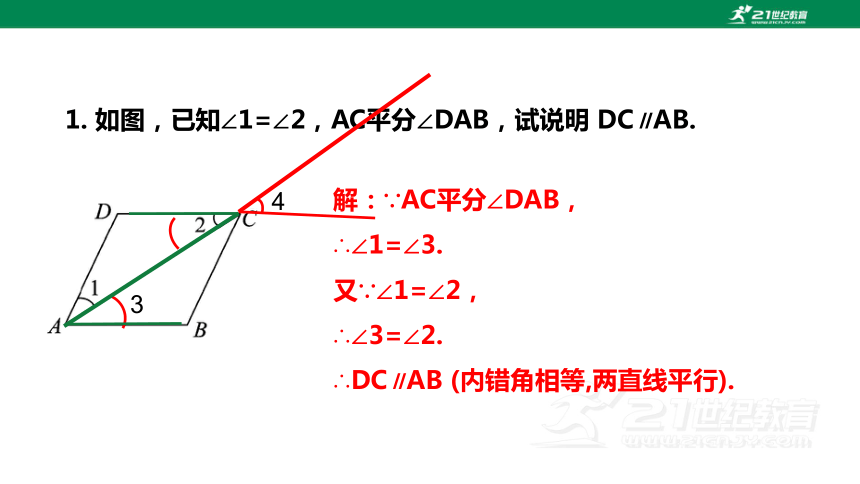
1. 如图,已知∠1=∠2,AC平分∠DAB,试说明 DC∥AB.
解:∵AC平分∠DAB,
∴∠1=∠3.
又∵∠1=∠2,
∴∠3=∠2.
∴DC∥AB (内错角相等,两直线平行).
3
4
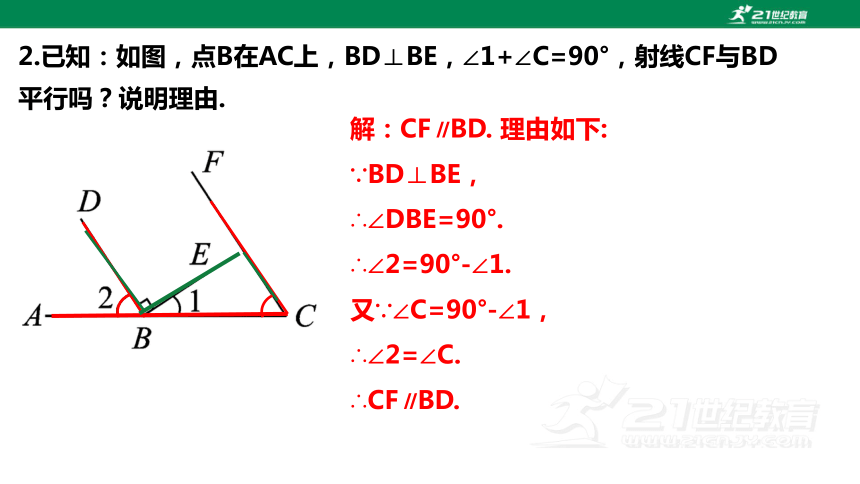
2.已知:如图,点B在AC上,BD⊥BE,∠1+∠C=90°,射线CF与BD平行吗?说明理由.
解:CF∥BD. 理由如下:
∵BD⊥BE,
∴∠DBE=90°.
∴∠2=90°-∠1.
又∵∠C=90°-∠1,
∴∠2=∠C.
∴CF∥BD.
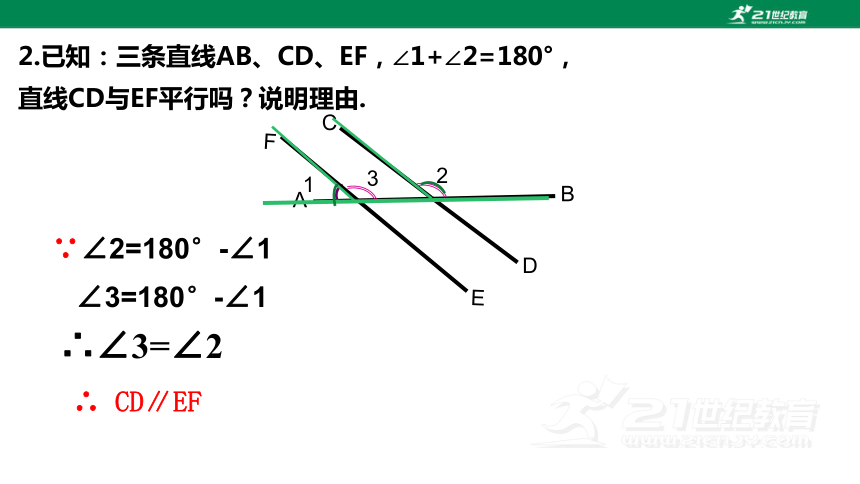
∵∠2=180°-∠1
1
2
A
B
C
D
E
F
3
∠3=180°-∠1
∴∠3=∠2
∴ CD∥EF
2.已知:三条直线AB、CD、EF,∠1+∠2=180°,
直线CD与EF平行吗?说明理由.
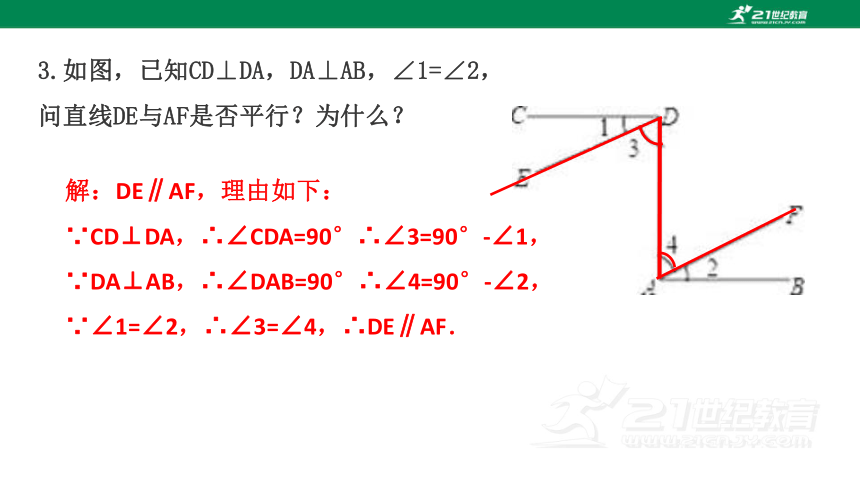
3.如图,已知CD⊥DA,DA⊥AB,∠1=∠2,问直线DE与AF是否平行?为什么?
解:DE∥AF,理由如下:
∵CD⊥DA,∴∠CDA=90°∴∠3=90°-∠1,
∵DA⊥AB,∴∠DAB=90°∴∠4=90°-∠2,
∵∠1=∠2,∴∠3=∠4,∴DE∥AF.
四.
∵∠C+∠2=90°
∠1=∠C
∴∠1+∠2=90°
∴ DE∥BC(同旁内角互补,两直线平行)
∵DE⊥BE
∴∠E=90°
∴∠E+∠EBC=∠E+∠1+∠2=90°+90°=180°
解 DE∥BC,理由如下:
4:如图DE⊥EB于点E,∠1=∠C,∠2与∠C互为余角.
判断DE与BC是否平行,并说明理由.
5、如图,已知DE、BF分别平分∠ADC和∠ABC, ∠1=∠2, ∠ADC=∠ABC,由此可以推出图中哪些线段平行?请写出理由。
证明:∵ ∠1=∠2(已知)
∴DE∥BF
(同位角相等,两直线平行)
∵DE、BF分别是∠ADC、∠ABC的平分线
∴ ∠1= ∠ABC,∠3= ∠ADC
∵
∠ADC=∠ABC
∴ ∠1=∠3
∴
AB∥CD( )
∵ ∠1=∠2
∴ ∠2=∠3
内错角相等,两直线平行
6.如图,已知AD⊥BC,FG⊥BC,垂足分别为D,G,∠1=∠2,
试猜想∠BDE与∠C的大小关系,并说明理由.
解:∠BDE=∠C.理由如下:
∵AD⊥BC,FG⊥BC,∴AD∥FG.
∴∠1=∠3.
又∵∠1=∠2,∴∠2=∠3.
∴DE∥AC. ∴∠BDE=∠C.
3
4
7.如图,CD∥EF,∠1=∠2,求证:∠3=∠ACB.
解:∵CD∥EF(已知)
∴∠4=∠2(两直线平行,同位角相等)
∵∠1=∠2
∴∠4=∠1
∴BC // DG(内错角角相等,两直线平行)
∴∠3=∠ACB(两直线平行,同位角相等)
4
一判:
等角
F、Z
非F、Z
F、Z、u
两角互补
U
非U
F、Z、U
两角互余:
F、Z、U
等角、两角互补:
等角、两角互补:
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
浙教版七年级下册
第一章 相交线与平行线 章末复习
想:一判二推三要使,
写,条分缕析,分步表达
一判:
等角
F、Z
非F、Z
F、Z、u
两角互补
U
非U
F、Z、U
两角互余:
F、Z、U
等角、两角互补:
等角、两角互补:
1. 如图,已知∠1=∠2,AC平分∠DAB,试说明 DC∥AB.
解:∵AC平分∠DAB,
∴∠1=∠3.
又∵∠1=∠2,
∴∠3=∠2.
∴DC∥AB (内错角相等,两直线平行).
3
4
2.已知:如图,点B在AC上,BD⊥BE,∠1+∠C=90°,射线CF与BD平行吗?说明理由.
解:CF∥BD. 理由如下:
∵BD⊥BE,
∴∠DBE=90°.
∴∠2=90°-∠1.
又∵∠C=90°-∠1,
∴∠2=∠C.
∴CF∥BD.
∵∠2=180°-∠1
1
2
A
B
C
D
E
F
3
∠3=180°-∠1
∴∠3=∠2
∴ CD∥EF
2.已知:三条直线AB、CD、EF,∠1+∠2=180°,
直线CD与EF平行吗?说明理由.
3.如图,已知CD⊥DA,DA⊥AB,∠1=∠2,问直线DE与AF是否平行?为什么?
解:DE∥AF,理由如下:
∵CD⊥DA,∴∠CDA=90°∴∠3=90°-∠1,
∵DA⊥AB,∴∠DAB=90°∴∠4=90°-∠2,
∵∠1=∠2,∴∠3=∠4,∴DE∥AF.
四.
∵∠C+∠2=90°
∠1=∠C
∴∠1+∠2=90°
∴ DE∥BC(同旁内角互补,两直线平行)
∵DE⊥BE
∴∠E=90°
∴∠E+∠EBC=∠E+∠1+∠2=90°+90°=180°
解 DE∥BC,理由如下:
4:如图DE⊥EB于点E,∠1=∠C,∠2与∠C互为余角.
判断DE与BC是否平行,并说明理由.
5、如图,已知DE、BF分别平分∠ADC和∠ABC, ∠1=∠2, ∠ADC=∠ABC,由此可以推出图中哪些线段平行?请写出理由。
证明:∵ ∠1=∠2(已知)
∴DE∥BF
(同位角相等,两直线平行)
∵DE、BF分别是∠ADC、∠ABC的平分线
∴ ∠1= ∠ABC,∠3= ∠ADC
∵
∠ADC=∠ABC
∴ ∠1=∠3
∴
AB∥CD( )
∵ ∠1=∠2
∴ ∠2=∠3
内错角相等,两直线平行
6.如图,已知AD⊥BC,FG⊥BC,垂足分别为D,G,∠1=∠2,
试猜想∠BDE与∠C的大小关系,并说明理由.
解:∠BDE=∠C.理由如下:
∵AD⊥BC,FG⊥BC,∴AD∥FG.
∴∠1=∠3.
又∵∠1=∠2,∴∠2=∠3.
∴DE∥AC. ∴∠BDE=∠C.
3
4
7.如图,CD∥EF,∠1=∠2,求证:∠3=∠ACB.
解:∵CD∥EF(已知)
∴∠4=∠2(两直线平行,同位角相等)
∵∠1=∠2
∴∠4=∠1
∴BC // DG(内错角角相等,两直线平行)
∴∠3=∠ACB(两直线平行,同位角相等)
4
一判:
等角
F、Z
非F、Z
F、Z、u
两角互补
U
非U
F、Z、U
两角互余:
F、Z、U
等角、两角互补:
等角、两角互补:
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
